- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логарифмическая функция. Математика, 10 класс. презентация
Содержание
- 1. Логарифмическая функция. Математика, 10 класс.
- 2. Содержание темы: 1. Краткий исторический экскурс. 2.
- 3. Результатом изучения темы является: 1. Знание определения
- 4. Исторический очерк. XVI в. резко возрос
- 5. Первые таблицы логарифмов составлены независимо
- 6. Первые таблицы десятичных логарифмов (1617 г.) были
- 7. Непер Джон(1550—1617) —английский математик. Изобретатель логарифмов, составитель первой таблицы логарифмов, палочек Непера.
- 8. Логарифм -определяется как показатель степени,
- 9. Вещественный логарифм Логарифм вещественного числа имеет смысл
- 10. Наиболее широкое применение нашли следующие виды логарифмов:
- 11. Логарифмическая функция Функция вида f(x)
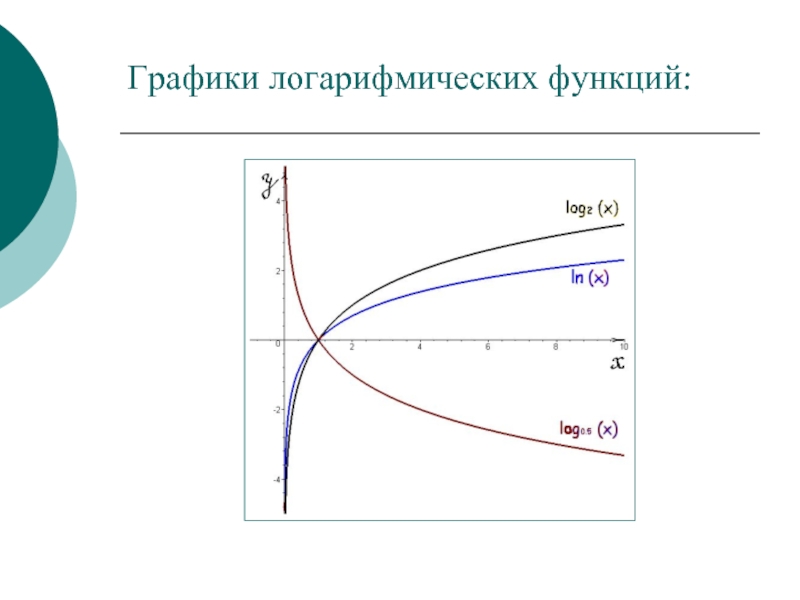
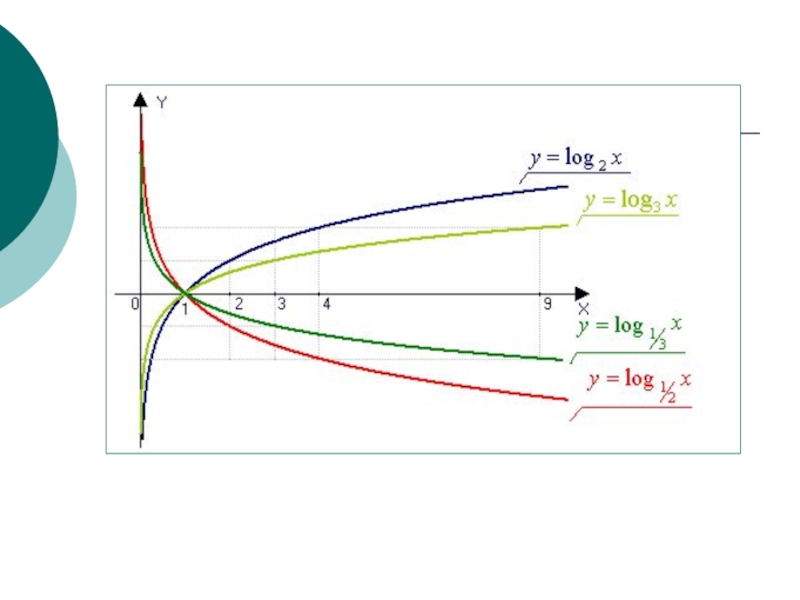
- 12. Графики логарифмических функций:
- 13. Свойства функции: Область определения (0; +∞) Область
- 14. Параллельный перенос вдоль оси ОХ:
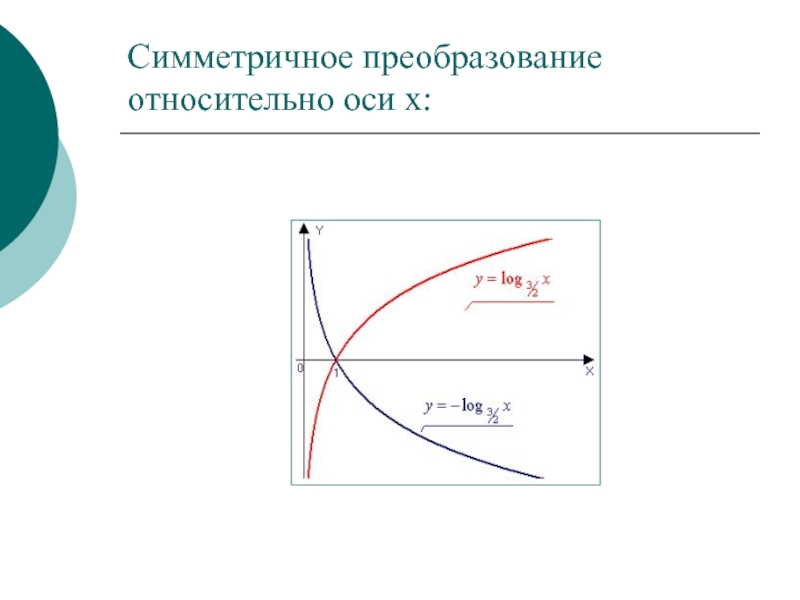
- 15. Симметричное преобразование относительно оси у:
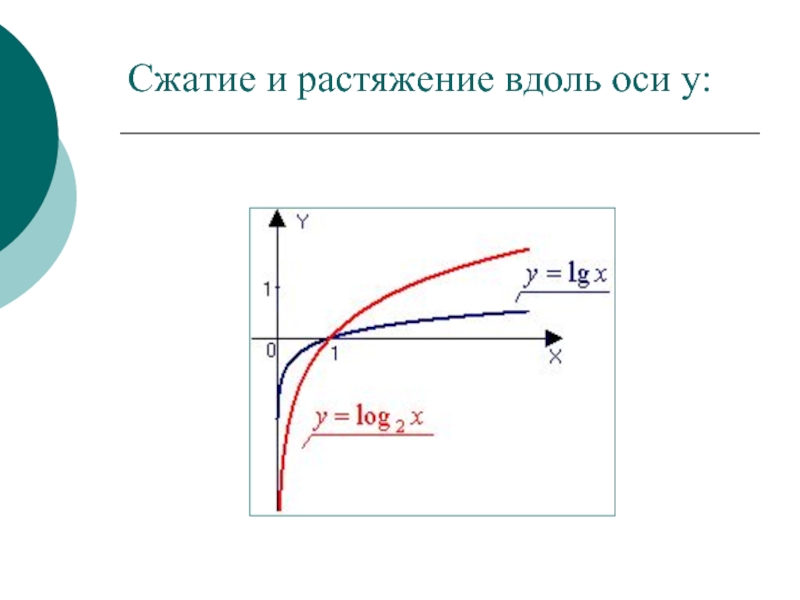
- 16. Сжатие и растяжение вдоль оси y:
- 17. Симметричное преобразование относительно оси х:
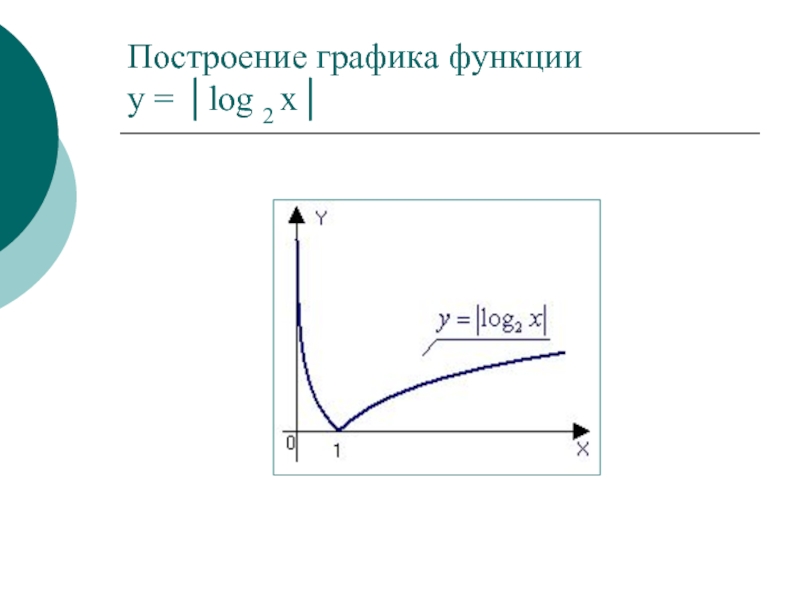
- 18. Построение графика функции y = │log 2 х│
- 20. Десятичные логарифмы Логарифмы по основанию 10 (обозначение:
- 21. Свойства логарифмов:
- 22. Примеры заданий Единого Государственного Экзамена:
- 23. Примеры заданий Единого Государственного Экзамена:
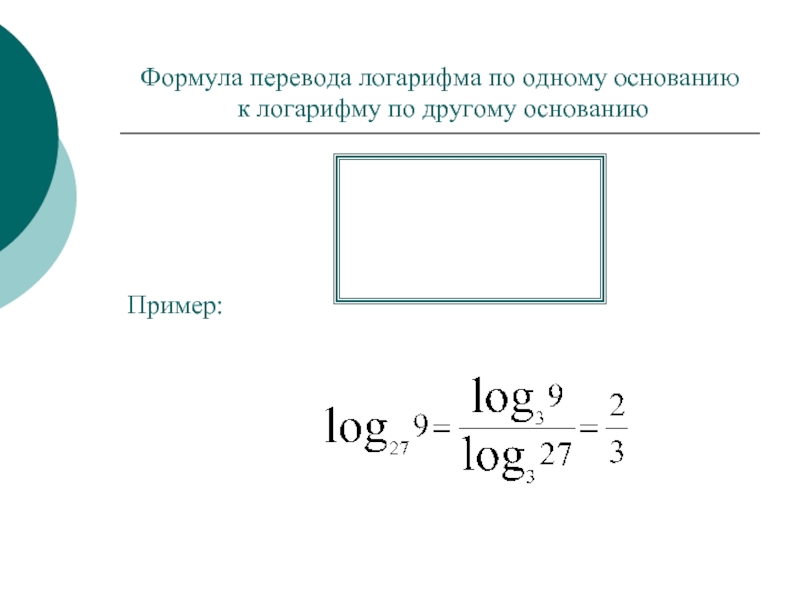
- 24. Формула перевода логарифма по одному основанию
- 25. Логарифмическое уравнение. Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Примеры:
- 26. Уравнения: решаемые по определению логарифма; приводимые к квадратному.
- 27. Метод потенцирования; Метод логарифмирования.
- 28. Риманова поверхность: Комплексная логарифмическая функция —
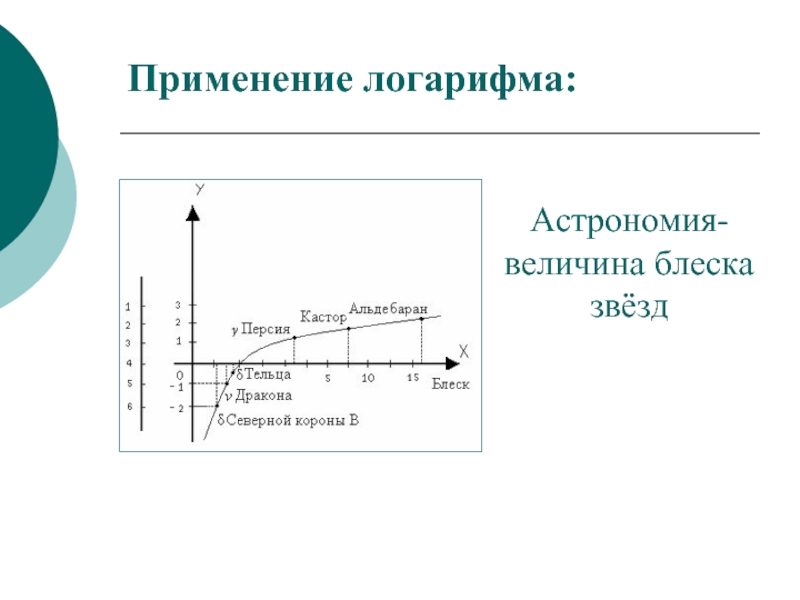
- 29. Применение логарифма: Астрономия-величина блеска звёзд
- 30. Логарифмическая спираль: Форму логарифмической спирали имеют
- 31. Применение логарифмической функции: Логарифмическая функция крайне важна
- 32. Выполнить самостоятельно: По учебнику «Алгебра и начала
Слайд 2Содержание темы:
1. Краткий исторический экскурс.
2. Определение логарифма числа.
3. График логарифмической функции.
4.
Линейные преобразования графиков логарифмической функции.
5. Свойства логарифмов.
6. Логарифмические уравнения. Классификация по методам решения.
5. Свойства логарифмов.
6. Логарифмические уравнения. Классификация по методам решения.
Слайд 3Результатом изучения темы является:
1. Знание определения «Логарифм числа».
2. Знание свойств логарифмов.
3.
Умение выполнять преобразования логарифмических выражений на основе применения свойств логарифмов.
4. Умение решать основные типы логарифмических уравнений.
5. Знание свойств логарифмической функции.
4. Умение решать основные типы логарифмических уравнений.
5. Знание свойств логарифмической функции.
Слайд 4Исторический очерк.
XVI в. резко возрос объем работы, связанный с вычислениями. Поэтому
открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов, необычайно быстро вошли в практику.
Слайд 5 Первые таблицы логарифмов составлены независимо друг от друга шотландским
математиком Дж. Непером (1550—1617) и швейцарцем И. Бюрги (1552—1632).
Непер Джон.
Слайд 6Первые таблицы десятичных логарифмов (1617 г.) были составлены по совету Непера
английским математиком Г. Бриггсом (1561 —1630). Многие из них были найдены с помощью выведенной Бриггсом приближенной формулы:
Слайд 7Непер Джон(1550—1617) —английский математик. Изобретатель логарифмов, составитель первой таблицы логарифмов, палочек
Непера.
Слайд 8Логарифм
-определяется как показатель степени, в которую надо возвести основание
a, чтобы получить число b.
Слайд 9Вещественный логарифм Логарифм вещественного числа имеет смысл при а > 0, а
≠ 1, b > 0.
Логарифм:
Слайд 10Наиболее широкое применение нашли следующие виды логарифмов:
Натуральные: ,
основание: e (число Эйлера).
Десятичные: , основание: число 10.
Двоичные: , основание: число 2. Они применяются в теории информации и информатике.
Десятичные: , основание: число 10.
Двоичные: , основание: число 2. Они применяются в теории информации и информатике.
Слайд 11Логарифмическая функция
Функция вида f(x) = log a x, определённая
при
График любой логарифмической функции проходит через точку (1;0). Функция непрерывна в своей области определения.
График любой логарифмической функции проходит через точку (1;0). Функция непрерывна в своей области определения.
Слайд 13Свойства функции:
Область определения (0; +∞)
Область значений: у R
Чётность /нечётность:
функция не является ни четной, ни нечетной
Нули функции: y = 0 при x = 1
Промежутки знакопостоянства: если 0 < a < 1, то y > 0 при x (0; 1), y < 0 при x (1; ) если a > 1, то y > 0 при x (1; ), y < 0 при x (0; 1)
Монотонность:
при 0 < a < 1 функция убывает при x (0; +∞ );
при a > 1 функция возрастает при x (0; +∞ )
Экстремумов нет.
График функции проходит через точку: (1; 0)
Асимптота x = 0
Нули функции: y = 0 при x = 1
Промежутки знакопостоянства: если 0 < a < 1, то y > 0 при x (0; 1), y < 0 при x (1; ) если a > 1, то y > 0 при x (1; ), y < 0 при x (0; 1)
Монотонность:
при 0 < a < 1 функция убывает при x (0; +∞ );
при a > 1 функция возрастает при x (0; +∞ )
Экстремумов нет.
График функции проходит через точку: (1; 0)
Асимптота x = 0
Слайд 20Десятичные логарифмы
Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов
широко применялись для вычислений.
Слайд 25Логарифмическое уравнение.
Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим.
Примеры:
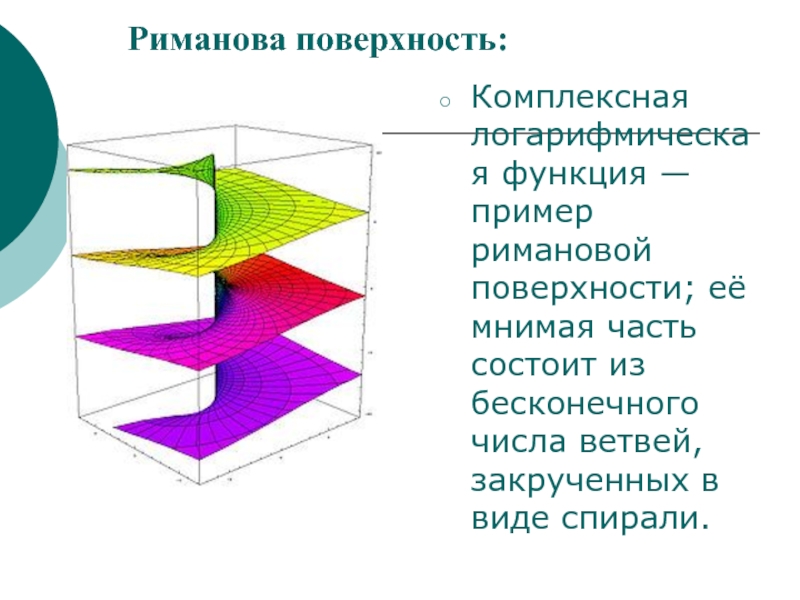
Слайд 28Риманова поверхность:
Комплексная логарифмическая функция — пример римановой поверхности; её мнимая часть
состоит из бесконечного числа ветвей, закрученных в виде спирали.
Слайд 30Логарифмическая спираль:
Форму логарифмической спирали имеют не только объекты астрономии, но и,
например, ракушки многих улиток, рога козлов, паутина паука, семечки подсолнуха.
Слайд 31Применение логарифмической функции:
Логарифмическая функция крайне важна в экономике, физике, при проведении
научных, экспериментальных расчетов, астрономии и др. Форма логарифмической спирали присуща многим природным объектам.
Физика — интенсивность звука (децибелы).
Астрономия — шкала яркости звёзд.
Химия — активность водородных ионов (pH).
Сейсмология — шкала Рихтера.
Теория музыки — нотная шкала, по отношению к частотам нотных звуков.
История — логарифмическая шкала времени.
Физика — интенсивность звука (децибелы).
Астрономия — шкала яркости звёзд.
Химия — активность водородных ионов (pH).
Сейсмология — шкала Рихтера.
Теория музыки — нотная шкала, по отношению к частотам нотных звуков.
История — логарифмическая шкала времени.
Слайд 32Выполнить самостоятельно:
По учебнику «Алгебра и начала анализа 10-11» (Алимов Ш. А.
и другие):
1. § 15, стр. 90, № 267- 270.
2. № 274.
3. § 16, стр. 93, № 290, 298*.
4. § 17, стр. 97, № 306.
5. § 18, стр. 101, № 321.
6. § 19, стр. 106, № 337, 340.
1. § 15, стр. 90, № 267- 270.
2. № 274.
3. § 16, стр. 93, № 290, 298*.
4. § 17, стр. 97, № 306.
5. § 18, стр. 101, № 321.
6. § 19, стр. 106, № 337, 340.