- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лист Мёбиуса презентация
Содержание
- 1. Лист Мёбиуса
- 2. ЦЕЛЬ ИССЛЕДОВАНИЯ: Изучить лист Мебиуса
- 3. ЗАДАЧИ ИССЛЕДОВАНИЯ Изучить историю появления листа
- 4. ЛИСТ МЕБИУСА Таинственный и знаменитый лист
- 5. КАК СДЕЛАТЬ ЛИСТ МЕБИУСА? Лист Мёбиуса, поверхность,
- 6. СФЕРЫ ПРИМЕНЕНИЯ ЛИСТА МЕБИУСА Создание скульптур, литографий
- 7. СФЕРЫ ПРИМЕНЕНИЯ ЛИСТА МЕБИУСА Научная фантастика
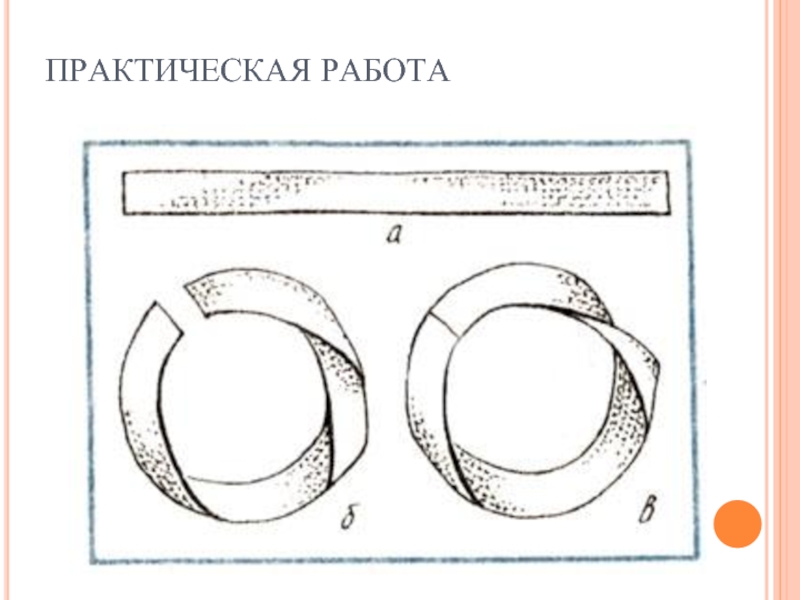
- 8. ПРАКТИЧЕСКАЯ РАБОТА
- 9. СКЛЕИМ ДВА КОЛЬЦА – ОДНО ПРОСТОЕ,
- 10. ЕСЛИ НА
- 11. ЕСЛИ ВЗЯТЬ ДВА РАЗНЫХ КОЛЬЦА И
- 12. БЕРЕМ ДВА КОЛЬЦА – ОДНО ПРОСТОЕ,
- 13. ДАВАЙТЕ ПОСМОТРИМ! http://school-collection.edu.ru/catalog/rubr/6f294dad-b780-11db-8314-0800200c9a66/76321/
- 14. НЕСКОЛЬКО РАЗРЕЗОВ (ПРЕДЛАГАЕМ ПОЭКСПЕРИМЕНТИРОВАТЬ ДОМА) Что
- 15. НЕСКОЛЬКО ЛЕНТ Берем два кольца: одно простое,
- 16. НЕСКОЛЬКО ПЕРЕКРУЧИВАНИЙ Будем перекручивать кольцо при склеивании несколько раз и разрежем его вдоль
- 17. ВЫВОДЫ Понятия и теоремы топологии полезны математикам
Слайд 3ЗАДАЧИ ИССЛЕДОВАНИЯ
Изучить историю появления листа Мебиуса, его виды и сферы применения
Опытным
Слайд 4ЛИСТ МЕБИУСА
Таинственный и знаменитый лист Мёбиуса (иногда говорят: лента Мёбиуса) придумал
Август Фердинанд Мёбиус
(1790-1768).
Слайд 5КАК СДЕЛАТЬ ЛИСТ МЕБИУСА?
Лист Мёбиуса, поверхность, получающаяся при склеивании двух противоположных
Чтобы превратить квадрат в лист Мёбиуса, необходимо соединить края, помеченные A так, чтобы направления стрелок совпали.
Слайд 6СФЕРЫ ПРИМЕНЕНИЯ ЛИСТА МЕБИУСА
Создание скульптур, литографий
Художник ЭшерХудожник Эшер создал несколько литографий,
Слайд 7СФЕРЫ ПРИМЕНЕНИЯ ЛИСТА МЕБИУСА
Научная фантастика
Артур Кларк. Стена Темноты.
А. Дж. Дейч.
Ленточный конвейер
Резистор Мебиуса
Слайд 9СКЛЕИМ ДВА КОЛЬЦА – ОДНО ПРОСТОЕ, ОДНО ПЕРЕКРУЧЕННОЕ. ЧТО ПОЛУЧИТСЯ, ЕСЛИ
Результат:
в первом кольце линия прошла по одной стороне (у кольца 2 стороны)
Во втором кольце линия прошла по обеим сторонам кольца, хотя карандаш не отрывался от бумаги (у кольца одна сторона!)
У ленты, из которой сделан лист Мёбиуса, две стороны. А у него самого, оказывается, есть только одна сторона!
Слайд 10 ЕСЛИ НА ВНУТРЕННЮЮ СТОРОНУ ОБЫЧНОГО КОЛЬЦА
Слайд 11ЕСЛИ ВЗЯТЬ ДВА РАЗНЫХ КОЛЬЦА И ЗАКРАСИТЬ ИХ (ПРЕДЛАГАЕМ ВАМ СДЕЛАТЬ
Получим результат:
закрашена одна сторона
весь лист закрашен в один цвет
"Если кто-нибудь вздумает раскрасить "только одну" сторону поверхности мёбиусовой ленты, пусть лучше сразу погрузит ее всю в ведро с краской"- пишут Рихард Курант и Герберт Робинс в книге "Что такое математика".
Слайд 12БЕРЕМ ДВА КОЛЬЦА – ОДНО ПРОСТОЕ, ОДНО ПЕРЕКРУЧЕННОЕ (ЛИСТ МЕБИУСА) РАЗРЕЖЕМ ВДОЛЬ
Результат:
Из первого кольца получилось 2 новых кольца
Из листа Мебиуса получилось 1 кольцо
Слайд 13ДАВАЙТЕ ПОСМОТРИМ!
http://school-collection.edu.ru/catalog/rubr/6f294dad-b780-11db-8314-0800200c9a66/76321/
Слайд 14НЕСКОЛЬКО РАЗРЕЗОВ
(ПРЕДЛАГАЕМ ПОЭКСПЕРИМЕНТИРОВАТЬ ДОМА)
Что получится, если разрезать кольцо вдоль, отступив
Возьмем ленту шириной 5 см, на которой нанесен пунктир, отступив от края на1 см, 2 см, 3 см и 4 см. Сделаем из неё лист Мёбиуса. Что получится, если разрезать его по пунктиру?
Результат:
Получим 3 кольца:
кольцо - лист Мёбиуса - 1 перекрут, ширина 1 см, длина равна длине исходного кольца.
II, III - кольца с двумя перекрутами, ширина 1 см, длина в 2 раза больше исходного листа.
II и III кольцо сцеплены с I кольцом и между собой.
Слайд 15НЕСКОЛЬКО ЛЕНТ
Берем два кольца: одно простое, одно Мебиусово. Склеиваем их под
Результат: получим одно кольцо
Слайд 16НЕСКОЛЬКО ПЕРЕКРУЧИВАНИЙ
Будем перекручивать кольцо при склеивании несколько раз и разрежем его
Слайд 17ВЫВОДЫ
Понятия и теоремы топологии полезны математикам почти всех специальностей. Она используется
Изучение листа Мёбиуса - хорошее введение к элементам топологии.
В программу школьного курса математики изучение листа Мебиуса не входит, однако учитель может познакомить учащихся с этой интересной поверхностью во время занятий математического кружка, воспользовавшись материалами нашего исследования и презентацией
Во время декады математики в следующем учебном году мы планируем мое выступление перед учениками начальной школы