- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейные электрические цепи однофазного переменного тока презентация
Содержание
- 1. Линейные электрические цепи однофазного переменного тока
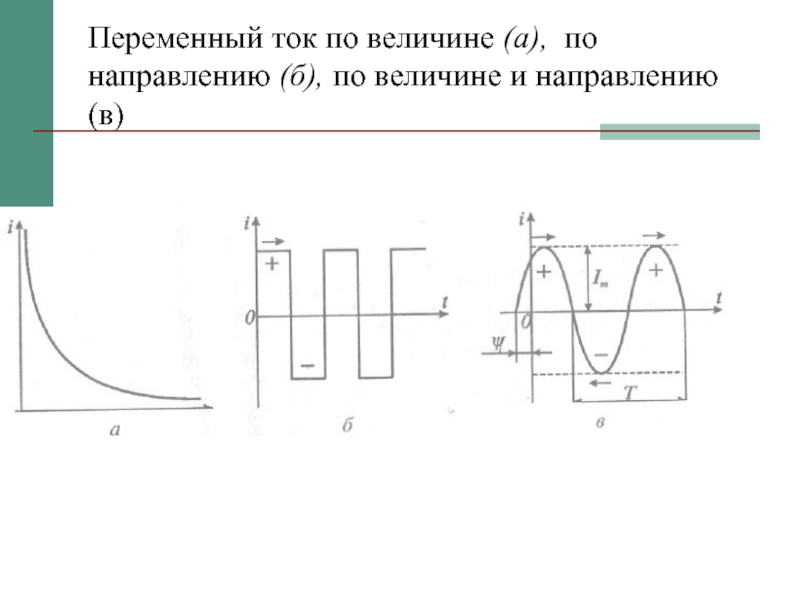
- 2. Переменный ток по величине (а), по направлению (б), по величине и направлению (в)
- 3. Параметры синусоидального тока Период переменного тока Частота
- 4. Действующие значения тока, напряжения, эдс синусоидального тока
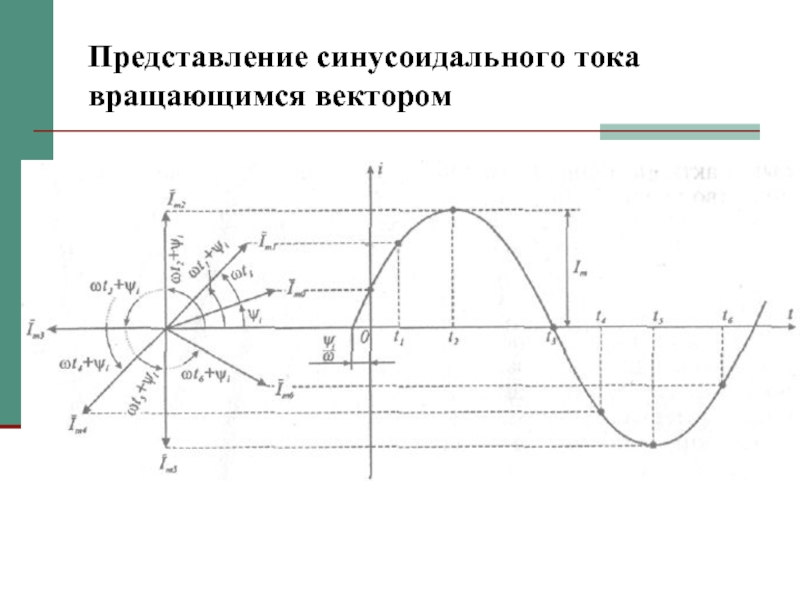
- 5. Представление синусоидального тока вращающимся вектором
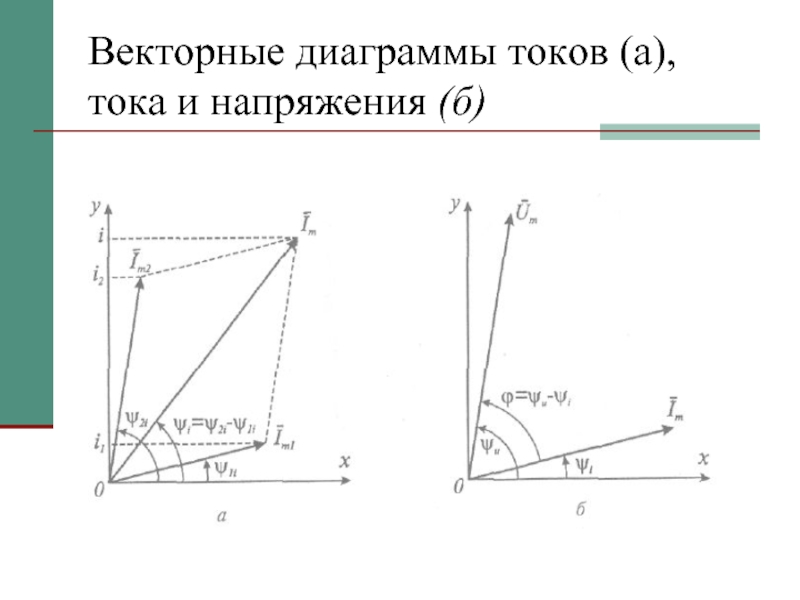
- 6. Векторные диаграммы токов (а), тока и напряжения (б)
- 7. Период переменного тока Синусоидальный ток является частным
- 8. Частота колебаний Величина, обратная периоду, называется частотой
- 9. Синусоидальный ток Повсеместное применение получил периодический ток,
- 10. Фаза Аргумент α t = ωt +
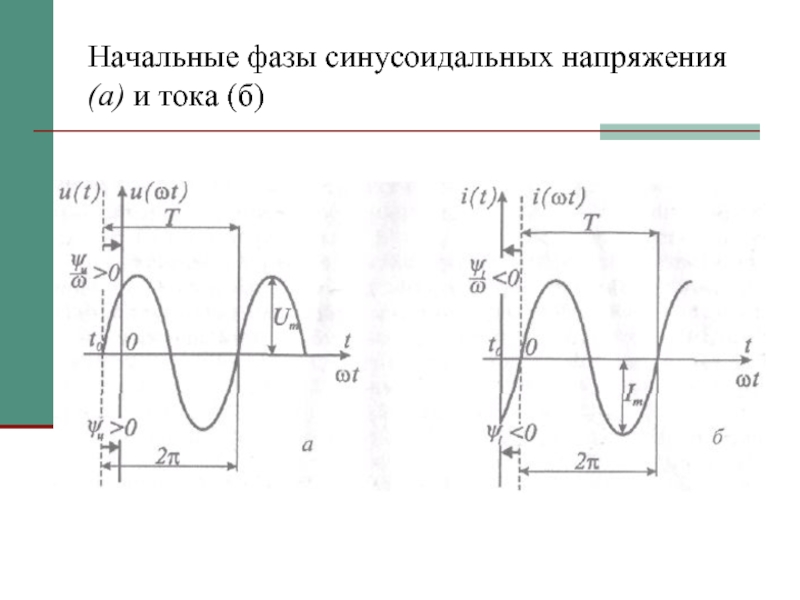
- 11. Начальные фазы синусоидальных напряжения (а) и тока (б)
- 12. Векторная диаграмма Совокупность векторов, изображающих синусоидальные токи,
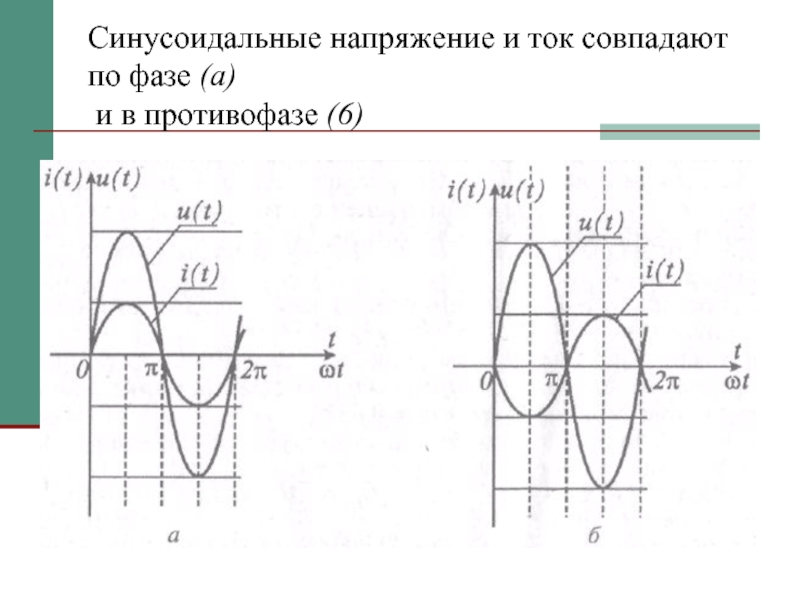
- 13. Синусоидальные напряжение и ток совпадают по фазе (а) и в противофазе (6)
- 14. Среднее значение периодического переменного тока Среднее
- 15. Средневыпрямленный ток Средневыпрямленным током Icp, как средним
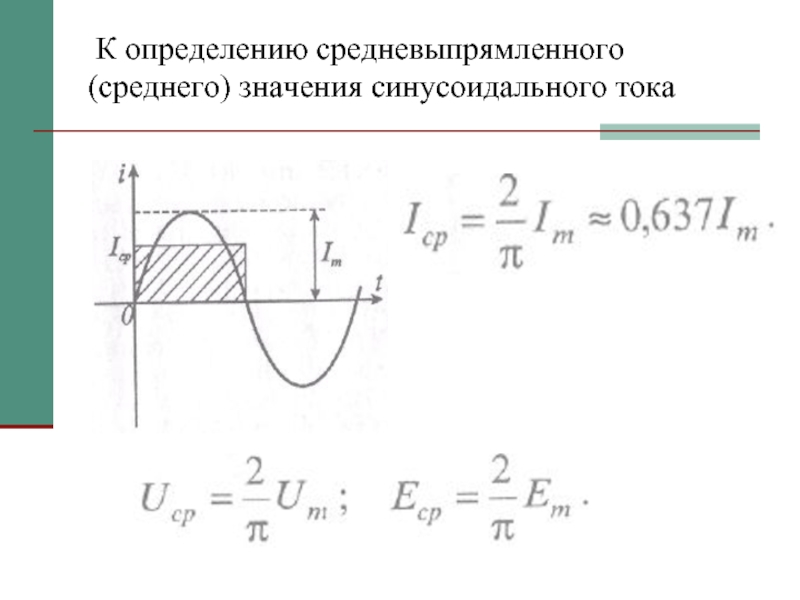
- 16. К определению средневыпрямленного (среднего) значения синусоидального тока
- 17. Действующее значение периодического переменного тока Действующее значение
- 18. Действующий ток где Ri
- 19. Представление синусоидального тока комплексными величинами Любое комплексное
- 20. Алгебраическая, тригонометрическая и показательная формы
- 21. Представление синусоидального тока вращающимся вектором Если
- 22. Комплексное число А (а) и оператор вращения (б)
- 23. Мнимая и вещественная части Мнимая часть представляет
- 24. Комплексный мгновенный и действующий синусоидальный ток
- 25. Изображение синусоидального тока комплексными величинами Синусоидальный
- 26. Изображение комплексного тока синусоидальным током Любая из
- 27. Уравнения для напряжений и эдс
- 28. Закон Ома для участка цепи синусоидального тока
- 29. Закон Ома для участка цепи синусоидального тока
- 30. Комплексное электрическое сопротивление
- 31. Комплексная проводимость Y
Переменный ток по величине (а), по направлению (б), по величине и направлению (в)
Слайд 3Параметры синусоидального тока
Период переменного тока
Частота колебаний
Амплитуда тока
Угловая частота
Начальная фаза
Фаза
Среднее значение тока
Действующее
значение тока
Слайд 7Период переменного тока
Синусоидальный ток является частным случаем периодического переменного тока, значение
которого в любой момент времени t определяется мгновенным током:
где k = 1,2,3 ...; Т– период переменного тока, измеряемый в секундах (с).
Периодом Т переменного тока i (t) называется промежуток времени t, через который цикл изменения тока повторяется, a k указывает на номер цикла.
где k = 1,2,3 ...; Т– период переменного тока, измеряемый в секундах (с).
Периодом Т переменного тока i (t) называется промежуток времени t, через который цикл изменения тока повторяется, a k указывает на номер цикла.
Слайд 8Частота колебаний
Величина, обратная периоду, называется частотой колебаний,
которая измеряется в герцах(Гц) и
указывает на число колебаний за одну секунду, т. е. на число периодов переменного тока, укладывающихся за время, равное одной секунде.
Слайд 9Синусоидальный ток
Повсеместное применение получил периодический ток, являющийся синусоидальной функцией времени и
называемый синусоидальным током
где Im - амплитуда тока,
ω = 2π/Т = 2πf— угловая частота,
ψ — начальная фаза.
где Im - амплитуда тока,
ω = 2π/Т = 2πf— угловая частота,
ψ — начальная фаза.
Слайд 10Фаза
Аргумент α t = ωt + ψi, измеряемый в градусах или
в радианах, определяет фазный угол синусоидальной функции тока в любой момент времени и называется фазой.
Если t =0, то α0 = ψi, есть начальная фаза тока, т. е. значение фазы синусоидального тока в начальный момент времени.
Если α0 = 0, то ψi = – ωt0 т. е. в точке t0 начальная фаза тока ψi < 0;
Если t =0, то α0 = ψi, есть начальная фаза тока, т. е. значение фазы синусоидального тока в начальный момент времени.
Если α0 = 0, то ψi = – ωt0 т. е. в точке t0 начальная фаза тока ψi < 0;
Слайд 12Векторная диаграмма
Совокупность векторов, изображающих синусоидальные токи, напряжения и ЭДС одинаковой частоты
в начальный (или в любой один и тот же) момент времени, называется векторной диаграммой.
Слайд 14Среднее значение периодического переменного тока
Среднее значение периодического переменного тока Iср за
период T обычно определяют из геометрических представлений: площадь прямоугольника с основанием Т/2 и высотой Iср приравнивают площади, ограниченной кривой тока i(t), т. е.
Слайд 15Средневыпрямленный ток
Средневыпрямленным током Icp, как средним значением тока за время положительной
полуволны, т. е. за половину периода:
Слайд 17Действующее значение периодического переменного тока
Действующее значение периодического переменного тока (действующий ток)
I определяют из энергетических представлений: действующий ток равен по величине такому постоянному току I, который в активном сопротивлении R за период Т выделяет такое количество энергии, как данный переменный ток i, т. е.
Слайд 18Действующий ток
где Ri 2dt - есть энергия, выделяемая периодическим переменным током
i в активном сопротивлении R за время dt.
Здесь под интеграл ток i входит в квадрате: отрицательная половина синусоидального тока дает такой же вклад в количество выделяемой энергии, как и положительная, поэтому интеграл берется за период Т.
Здесь под интеграл ток i входит в квадрате: отрицательная половина синусоидального тока дает такой же вклад в количество выделяемой энергии, как и положительная, поэтому интеграл берется за период Т.
Слайд 19Представление синусоидального тока комплексными величинами
Любое комплексное число, обозначаемое À или А,
можно изобразить на комплексной плоскости точкой с радиусом - вектором À и представить в алгебраической, тригонометрической и показательной формах.
Слайд 20
Алгебраическая, тригонометрическая и показательная формы комплексного числа
где -
модуль комплексного числа;
а – вещественная часть комплексного числа;
b — мнимая часть комплексного числа;
α = arctg b/a — аргумент комплексного числа.
а – вещественная часть комплексного числа;
b — мнимая часть комплексного числа;
α = arctg b/a — аргумент комплексного числа.
Слайд 21Представление синусоидального тока вращающимся вектором
Если аргумент α является линейной функцией времени
t, т.е. , то и графическое представление комплексной функции À(t) аналогично представлению синусоидального тока вращающимся вектором
Слайд 23Мнимая и вещественная части
Мнимая часть представляет собой синусоидальный ток.
Вещественная часть представляет
собой косинусоидальный ток.
Слайд 25Изображение синусоидального тока комплексными величинами
Синусоидальный ток
i(t) = Im1sin (ωtk
+ ψi),
имеющий амплитуду Iт, круговую частоту ω и начальную фазу ψi, однозначно изображается одной из комплексных величин: комплексным мгновенным синусоидальным током I(t), комплексной амплитудой тока I или комплексным током I.
имеющий амплитуду Iт, круговую частоту ω и начальную фазу ψi, однозначно изображается одной из комплексных величин: комплексным мгновенным синусоидальным током I(t), комплексной амплитудой тока I или комплексным током I.
Слайд 26Изображение комплексного тока синусоидальным током
Любая из комплексных величин
I m(t], Iт,
I может быть представлена синусоидальным током i(t).
Слайд 28Закон Ома для участка цепи синусоидального тока без источников ЭДС
Комплексная амплитуда
тока в цепи синусоидального тока равна
отношению комплексной амплитуды напряжения к комплексному электрическому сопротивлению цепи.
отношению комплексной амплитуды напряжения к комплексному электрическому сопротивлению цепи.
Слайд 29Закон Ома для участка цепи синусоидального тока без источников ЭДС
где Y=
1/Z - комплексная проводимость двухполюсника.
