- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Леонард Эйлер презентация
Содержание
- 1. Леонард Эйлер
- 2. Краткие биографические сведения
- 3. Прямая Эйлера Прямая Эйлера – прямая, которой
- 4. Построение Дан прямоугольный треугольник АСВ. Проведем медиану
- 5. Томас Симпсон Прямая Симпсона
- 6. Краткая биография
- 7. Прямая Симпсона
- 8. Построение Пусть дан треугольник
- 9. Эванджелиста Торричелли Точка Торричелли
- 10. Краткая биография Эванджелиста Торричелли
- 11. Точка Торричелли Точка Торричелли —это точка в плоскости треугольника, сумма расстояний от которой до вершин треугольника имеет наименьшее значение.
- 12. Построим на сторонах произвольного треугольника ABC вне
- 13. Свойства 1. Каждая сторона треугольника
Слайд 2Краткие биографические сведения
Идеальный математик 18 века -
так часто называют Эйлера. Он родился в 1707 году в маленькой тихой Швейцарии. Примерно в то же время переселилась в Базель из Голландии семья Бернулли: уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. По воле случая юный Эйлер попал в эту компанию. Но когда ребята подросли, выяснилось, что в Швейцарии не хватит места для их умов. Зато в России была учреждена в 1725 году Академия Наук. Русских ученых не хватало, и тройка друзей отправилась туда. Поначалу Эйлер расшифровывал дипломатические депеши, обучал молодых моряков высшей математике и астрономии, составлял таблицы для артиллерийской стрельбы и таблицы движения Луны.
В 26 лет Эйлер был избран российским академиком, но через 8 лет он переехал из Петербурга в Берлин. Там "король математиков" работал с 1741 по 1766 год; потом он покинул Берлин и вернулся в Россию. Удивительно: слава Эйлера не закатилась и после того, как ученого поразила слепота (вскоре после переезда в Петербург). В 1770-е годы вокруг Эйлера выросла Петербургская математическая школа, более чем наполовину состоявшая из русских ученых. Тогда же завершилась публикация главной его книги - "Основ дифференциального и интегрального исчисления".
В начале сентября 1783 Эйлер почувствовал легкое недомогание. 18 сентября 1789 года он еще занимался математическими исследованиями, но неожиданно потерял сознание и «прекратил вычислять и жить».
Эйлер похоронен на Смоленском лютеранском кладбище в Петербурге, откуда его прах перенесен осенью 1956 в Некрополь Александро-Невской лавры.
В 26 лет Эйлер был избран российским академиком, но через 8 лет он переехал из Петербурга в Берлин. Там "король математиков" работал с 1741 по 1766 год; потом он покинул Берлин и вернулся в Россию. Удивительно: слава Эйлера не закатилась и после того, как ученого поразила слепота (вскоре после переезда в Петербург). В 1770-е годы вокруг Эйлера выросла Петербургская математическая школа, более чем наполовину состоявшая из русских ученых. Тогда же завершилась публикация главной его книги - "Основ дифференциального и интегрального исчисления".
В начале сентября 1783 Эйлер почувствовал легкое недомогание. 18 сентября 1789 года он еще занимался математическими исследованиями, но неожиданно потерял сознание и «прекратил вычислять и жить».
Эйлер похоронен на Смоленском лютеранском кладбище в Петербурге, откуда его прах перенесен осенью 1956 в Некрополь Александро-Невской лавры.
Слайд 3Прямая Эйлера
Прямая Эйлера – прямая, которой принадлежат ортоцентр (точка пересечения высот)
, центроид (точка пересечения медиан) и центр описанной окружности треугольника.
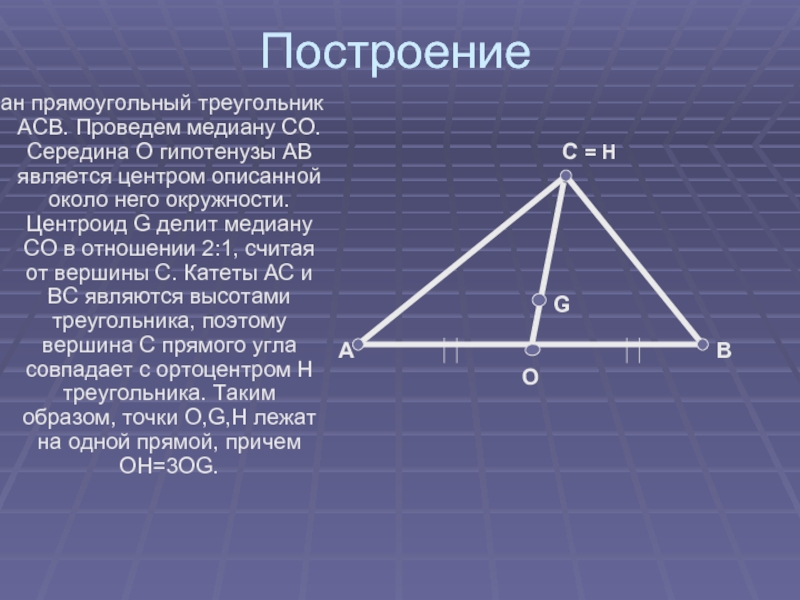
Слайд 4Построение
Дан прямоугольный треугольник АСВ. Проведем медиану СО. Середина O гипотенузы AB
является центром описанной около него окружности. Центроид G делит медиану CO в отношении 2:1, считая от вершины C. Катеты AC и BC являются высотами треугольника, поэтому вершина C прямого угла совпадает с ортоцентром H треугольника. Таким образом, точки O,G,H лежат на одной прямой, причем OH=3OG.
= Н
Слайд 6Краткая биография
Томас Симпсон(англ. Thomas Simpson) родился 20 августа 1710 года - английский математик. Занимаясь частными уроками математики и ремеслом ткача шелковых тканей, он работал над своим первым сочинением «A new treatise of fluxions» (Лондон), напечатанным в 1737 году. В 1740 году вышло в свет второе сочинение Симпсона, посвящённое теории вероятностей: «A treatise on the nature and laws of change». В 1746 году Симпсон избран в члены Лондонского королевского общества, а ранее — в члены основанного в 1717 году в Лондоне Математического общества. В 1758 избран иностранным членом Шведской королевской академии наук. Назначенный профессором в Королевскую военную академию в Вулидже, Симпсон составил учебники по элементарной математике. В особых отделах геометрии рассматриваются задачи о наибольших и наименьших величинах, решаемые с помощью элементарной геометрии, правильные многогранники, измерение поверхностей, объёмы тел и, наконец, смешанные задачи. Относительно учебника тригонометрии Симпсона следует заметить, что он отличается замечательною краткостью: он пользуется здесь, как изобретённым им новым средством доказательства, введением вспомогательного угла. Давно уже известное арабским ученым, это средство не было новостью в науке. Но в Европе до появления «Тригонометрии» Симпсона о нём не знали. Симпсон внёс упрощения в вычисление синусов и косинусов. Умер он в 1761 году.
Слайд 7Прямая Симпсона
Теорема
Основания перпендикуляров, опущенных из точки описанной окружности треугольника на его стороны или их продолжения, лежат на одной прямой. Эта прямая называется прямой Симпсона.
Основания перпендикуляров, опущенных из точки описанной окружности треугольника на его стороны или их продолжения, лежат на одной прямой. Эта прямая называется прямой Симпсона.
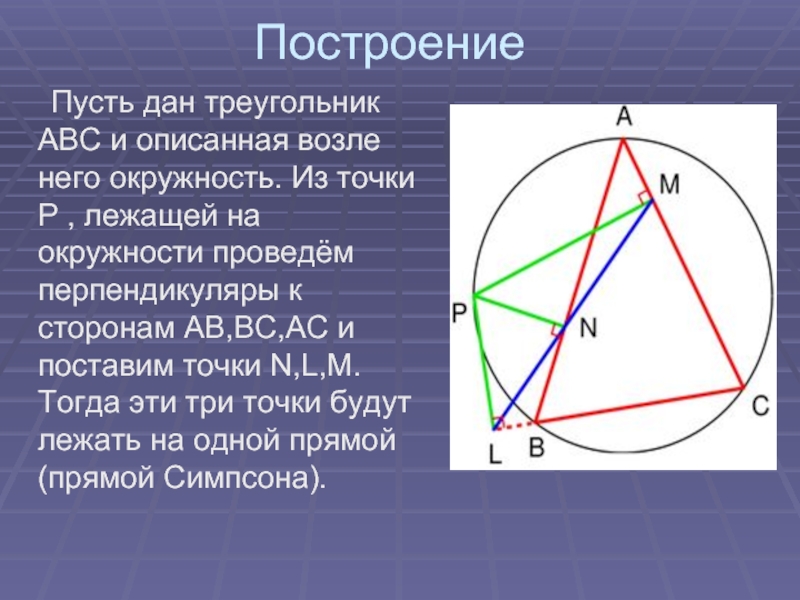
Слайд 8Построение
Пусть дан треугольник ABC и описанная возле него
окружность. Из точки P , лежащей на окружности проведём перпендикуляры к сторонам AB,BC,AC и поставим точки N,L,M. Тогда эти три точки будут лежать на одной прямой (прямой Симпсона).
Слайд 10Краткая биография
Эванджелиста Торричелли (итал. Evangelista Torricelli) родился 15 октября 1608
года в городке Фаэнца -итальянский математик и физик ученик Галилея. Известен как автор концепции атмосферного давления и продолжатель дела Галилея в области разработки новой механики. В 1627году приехал в Рим, где изучал математику под руководством Бенедетто Кастелли, друга и ученика Галилео Галилея. Под впечатлением трудов Галилея о движении написал собственное сочинение на ту же тему под названием «Трактат о движении» (1640). Торричелли препроводил своё сочинение Галилею, и последний, тогда уже слепой, пригласил его для сотрудничества при обработке своего последнего сочинения «Беседы о механике».
В 1641году Торричелли окончательно переехал к Галилею в Арчетри, где стал учеником и секретарем Галилея, а после смерти Галилея (1642) — его преемником на кафедре математики и философии Флорентийского университета.
В 1644году развил теорию атмосферного давления, доказал возможность получения так называемой «торричеллиевой пустоты» и изобрёл ртутный барометр.
Умер Торричелли во Флоренции 25 октября 1647 года.
В 1641году Торричелли окончательно переехал к Галилею в Арчетри, где стал учеником и секретарем Галилея, а после смерти Галилея (1642) — его преемником на кафедре математики и философии Флорентийского университета.
В 1644году развил теорию атмосферного давления, доказал возможность получения так называемой «торричеллиевой пустоты» и изобрёл ртутный барометр.
Умер Торричелли во Флоренции 25 октября 1647 года.
Слайд 11Точка Торричелли
Точка Торричелли —это точка в плоскости треугольника, сумма расстояний от которой до вершин треугольника имеет наименьшее значение. Если у треугольника наибольший угол
меньше 120 градусов, то это внутренняя точка треугольника, из которой все вершины треугольника видны под углом 120 градусов.
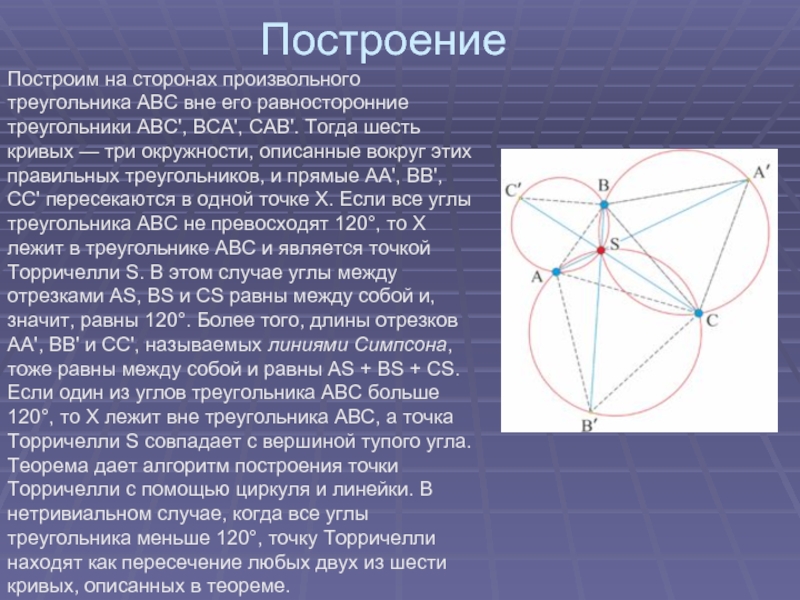
Слайд 12Построим на сторонах произвольного треугольника ABC вне его равносторонние треугольники ABC', BCA', CAB'.
Тогда шесть кривых — три окружности, описанные вокруг этих правильных треугольников, и прямые AA', BB', CC' пересекаются в одной точке X. Если все углы треугольника ABC не превосходят 120°, то X лежит в треугольнике ABC и является точкой Торричелли S. В этом случае углы между отрезками AS, BS и CS равны между собой и, значит, равны 120°. Более того, длины отрезков AA', BB' и CC', называемых линиями Симпсона, тоже равны между собой и равны AS + BS + CS. Если один из углов треугольника ABC больше 120°, то X лежит вне треугольника ABC, а точка Торричелли S совпадает с вершиной тупого угла.
Теорема дает алгоритм построения точки Торричелли с помощью циркуля и линейки. В нетривиальном случае, когда все углы треугольника меньше 120°, точку Торричелли находят как пересечение любых двух из шести кривых, описанных в теореме.
Теорема дает алгоритм построения точки Торричелли с помощью циркуля и линейки. В нетривиальном случае, когда все углы треугольника меньше 120°, точку Торричелли находят как пересечение любых двух из шести кривых, описанных в теореме.
Построение
Слайд 13Свойства
1. Каждая сторона треугольника из точки Торричелли видна под
углом 120 градусов;
2. Если один из углов треугольника равен 120 градусов, то точка Торричелли совпадет с вершиной треугольника.
3. Окружности описанные около правильных треугольников пересекаются в точке Торричелли.
4. Если внутри треугольника построить треугольник, стороны которого являются средними линиями исходного треугольника, потом аналогично построить третий, четвертый треугольник и т.д.; в каждом треугольнике построить свою точку Ферма - Торричелли, то все точки Ферма-Торричелли будут лежать на одной прямой. Это свойство будем называть коллинеарностью точек Торричелли.
2. Если один из углов треугольника равен 120 градусов, то точка Торричелли совпадет с вершиной треугольника.
3. Окружности описанные около правильных треугольников пересекаются в точке Торричелли.
4. Если внутри треугольника построить треугольник, стороны которого являются средними линиями исходного треугольника, потом аналогично построить третий, четвертый треугольник и т.д.; в каждом треугольнике построить свою точку Ферма - Торричелли, то все точки Ферма-Торричелли будут лежать на одной прямой. Это свойство будем называть коллинеарностью точек Торричелли.