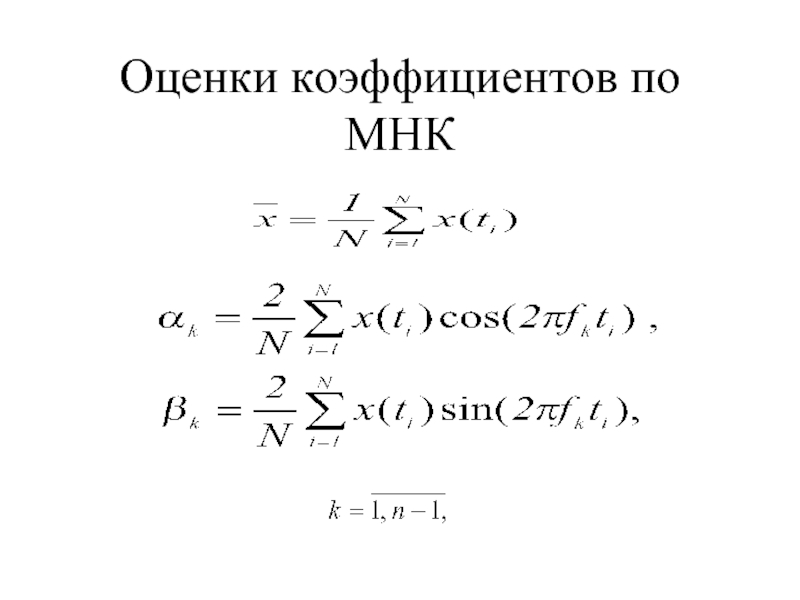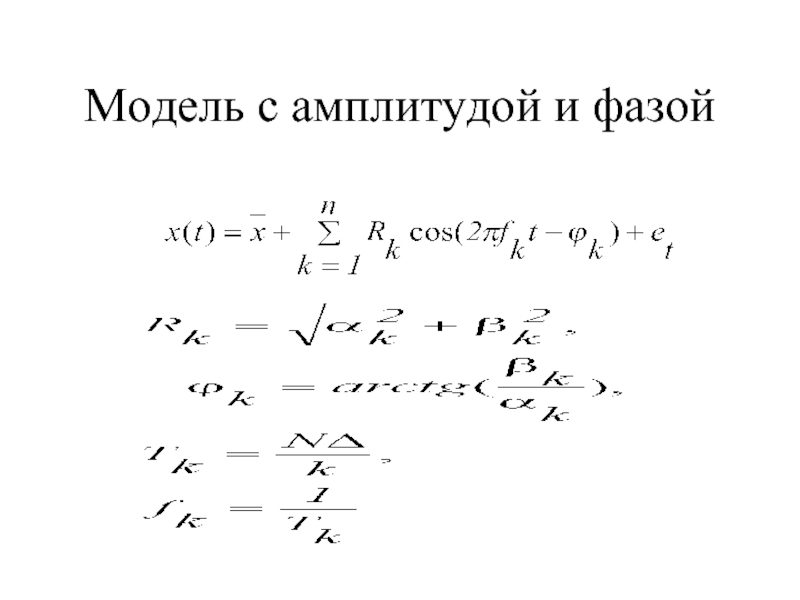- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 8 презентация
Содержание
- 1. Лекция 8
- 2. Случайная функция Это функция неслучайного аргумента, которая
- 3. Статистические характеристики случайной функции (изучает корреляционная теория)
- 4. Стационарный случайный процесс 1.Математическое ожидание постоянно (стационарность
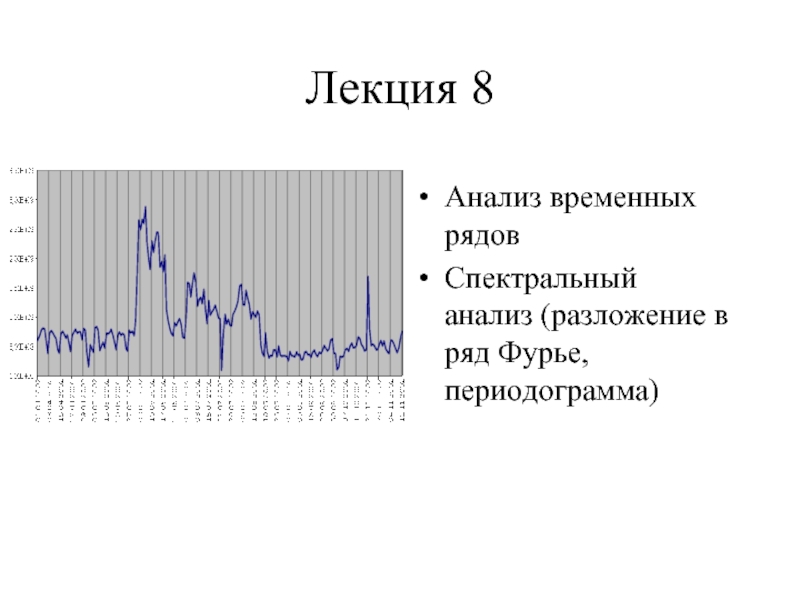
- 5. Анализ временных рядов Временной ряд - реализация
- 6. Временной ряд Реализация случайного процесса -
- 7. Визуализация временного ряда месячные международные авиаперевозки (в
- 8. Модель временного ряда Y(t) = f(t)+g(t)+ε(t) случайная составляющая периодическая (сезонная) составляющая тренд
- 9. Анализ тренда Не существует "автоматического" способа
- 10. Анализ периодической (сезонной) составляющей 1. Анализ автокорреляций
- 11. Анализ Фурье модель
- 12. Оценки коэффициентов по МНК
- 13. Оценки коэффициентов по МНК (продолжение)
- 14. Модель с амплитудой и фазой
- 15. Периодограмма или линейчатый спектр Фурье Интенсивность k-той гармоники
- 16. Оценка дисперсии величины x(ti)
- 17. 1. Выделение значимых гармоник по критерию Фишера
- 18. Выделение значимых гармоник по вкладу доминирующих гармоник в дисперсию
- 19. Модель после выделения гармоник
- 20. Алгоритм расчета коэффициентов разложения в ряд Фурье
- 21. Алгоритм расчета коэффициентов разложения в ряд Фурье
- 22. Алгоритм расчета коэффициентов разложения в ряд Фурье
- 23. Алгоритм расчета коэффициентов разложения в ряд Фурье
- 24. Литература http://education.iet.ru/files/text/econometrics/lect/
Слайд 2Случайная функция
Это функция неслучайного аргумента, которая
при каждом фиксированном значении аргумента
является случайной величиной
Случайный процесс
Неслучайный аргумент t-время
Слайд 3Статистические характеристики случайной функции (изучает корреляционная теория)
1. Математическое ожидание - неслучайная
функция -
при каждом значении t = мат. ожиданию сечения.
2. Дисперсия - неслучайная функция,
состоит из дисперсий сечений.
3. Корреляционная функция (автокорреляция)
равна коэффициенту корреляции между двумя
сечениями..
при каждом значении t = мат. ожиданию сечения.
2. Дисперсия - неслучайная функция,
состоит из дисперсий сечений.
3. Корреляционная функция (автокорреляция)
равна коэффициенту корреляции между двумя
сечениями..
Слайд 4Стационарный случайный процесс
1.Математическое ожидание постоянно (стационарность в широком смысле).
2. Автокорреляционная функция
зависит
только от разности аргумента.
только от разности аргумента.
В.Е. Гмурман. Теория вер. и мат. статистика. Стр. 386-449
Слайд 5Анализ временных рядов
Временной ряд - реализация
(траектория, выборочная функция)
случайной функции.
временным
рядом называют последовательность
наблюдений, упорядоченных по времени
наблюдений, упорядоченных по времени
Аргумент (t) дискретно меняется через равные
промежутки.
Слайд 6Временной ряд
Реализация случайного процесса -
неслучайная функция аргумента t (времени)
- результат экспериментов (опытов).
Временной ряд (случайная последовательность)
Аргумент (t) дискретно меняется через равные
промежутки.
Временной ряд (случайная последовательность)
Аргумент (t) дискретно меняется через равные
промежутки.
Слайд 7Визуализация временного ряда
месячные международные авиаперевозки (в тысячах)
в течение 12 лет.
(Бокс
и Дженкинс, 1976, стр. 531)
Слайд 8Модель временного ряда
Y(t) = f(t)+g(t)+ε(t)
случайная составляющая
периодическая (сезонная) составляющая
тренд
Слайд 9Анализ тренда
Не существует "автоматического" способа
обнаружения тренда в временном ряде.
Два
распространенных способа:
1) если тренд монотонный (возрастает или убывает), то используется регрессионный анализ;
2) если большая ошибка (разброс в значениях), то сначала делают сглаживание (окнами), потом регрессионный анализ.
1) если тренд монотонный (возрастает или убывает), то используется регрессионный анализ;
2) если большая ошибка (разброс в значениях), то сначала делают сглаживание (окнами), потом регрессионный анализ.
Слайд 10Анализ периодической (сезонной) составляющей
1. Анализ автокорреляций (процесс авторегрессии
и скользящего среднего АРПСС
- модель не
известна. Прогноз по предыдущим
значениям с осреднением)
2. Анализ Фурье. Периодограмма.
Отличие от АРПСС и
экспоненциального сглаживания -
периоды заранее неизвестны.
известна. Прогноз по предыдущим
значениям с осреднением)
2. Анализ Фурье. Периодограмма.
Отличие от АРПСС и
экспоненциального сглаживания -
периоды заранее неизвестны.