- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция презентация
Содержание
- 1. Лекция
- 2. Логика высказываний оперирует простейшими высказываниями, которые
- 3. В логике такие предложения, истинность которых
- 4. Определение предиката Формально предикат - функция, аргументами
- 5. Пример "Маша любит кашу"
- 6. Определение Предикат -
- 7. Определение Одноместным предикатом
- 8. Определение Двухместный предикат
- 9. Определение n-местный предикат -
- 10. Определение. Предикат называется
- 11. Логические операции над предикатами Замечание
- 12. Пример (Экзюпери) "Ты любишь потому,
- 13. Определение Присоединение квантора
- 14. Переменную х в предикате Р(х) называют
- 15. Переменная , на которую навешивается квантор
- 16. Пример Предикат "ВСЕ любят кашу": Возьмем отрицание
- 17. Кванторы общности и существования называют двойственными
- 18. Пример предикат "Собакам и кошкам вход воспрещен".
- 20. Пример
- 21. Свойства кванторов 1. Коммутативность одноименных кванторов 2. Перестановка кванторов общности и существования меняет смысл.
- 22. Основные законы, содержащие кванторы
- 23. Равносильные формулы логики предикатов Определение
- 24. Правила переноса кванторов через отрицание или
- 25. Правила переноса кванторов через отрицание или законы де Моргана для кванторов
- 27. «квантор можно вносить и выносить за скобки в конъюнкции»
- 28. постоянное высказывание можно вносить под знак
- 29. квантор существования можно вносить и выносить за скобки в дизъюнкции»
- 31. Нормальные формы формул логики предикатов
- 32. Среди нормальных форм формул логики предикатов
- 33. Пример Получили приведенную нормальную форму исходной формулы.
- 35. Алгоритм получения (приведения) ПНФ. Формула B
- 36. Шаг 1. Исключить связки эквивалентности (~)
- 37. Шаг 3. Удалить те квантификации, область
- 39. Скулемовские функции Приведение формулы ЛП к
- 40. Алгоритм получения сколемовской формы сопоставить каждой Ǝ-
- 41. 4) в матрице формулы заменить каждое
- 42. Клаузальная форма -сколемовская форма, матрица которой
Слайд 2
Логика высказываний оперирует простейшими высказываниями, которые могут быть или истинными, или
ложными.
В разговорном языке встречаются более сложные повествовательные предложения, истинность которых может меняться при изменении объектов, о которых идет речь.
В разговорном языке встречаются более сложные повествовательные предложения, истинность которых может меняться при изменении объектов, о которых идет речь.
Слайд 3
В логике такие предложения, истинность которых зависит от параметров, обозначают с
помощью предикатов.
"Предикат" с английского переводится как сказуемое.
"Предикат" с английского переводится как сказуемое.
Слайд 4Определение предиката
Формально предикат - функция, аргументами которой могут быть ПРОИЗВОЛЬНЫЕ ОБ'ЕКТЫ
из некоторого множества, а значения функции "истина" или "ложь".
Предикат можно рассматривать как расширение понятия высказывания.
Предикат можно рассматривать как расширение понятия высказывания.
Слайд 5Пример
"Маша любит кашу"
"Даша любит кашу"
"Саша любит
кашу«
предикат "Икс любит кашу"
и вместо неизвестного Икс могут быть либо Маша, либо Даша, либо Саша.
Подстановка вместо Икс имени конкретного ребенка превращает предикат в обычное высказывание.
предикат "Икс любит кашу"
и вместо неизвестного Икс могут быть либо Маша, либо Даша, либо Саша.
Подстановка вместо Икс имени конкретного ребенка превращает предикат в обычное высказывание.
Слайд 6
Определение
Предикат - это высказывание-функция, значение (истина/ложь) которого зависит
от параметров
Слайд 7
Определение
Одноместным предикатом Р(x) -произвольная функция переменного x, определенная
на множестве M и принимающая значение из множества {1; 0}.
"ВСЕ любят Игрека" - одноместный предикат.
Замечание
Высказывания – это 0(нуль)-местный предикат,
булева функция – n-местный предикат.
"ВСЕ любят КОЙ-КОГО [некоторого]" - нульместный предикат, то есть высказывание.
"ВСЕ любят Игрека" - одноместный предикат.
Замечание
Высказывания – это 0(нуль)-местный предикат,
булева функция – n-местный предикат.
"ВСЕ любят КОЙ-КОГО [некоторого]" - нульместный предикат, то есть высказывание.
Слайд 8
Определение
Двухместный предикат Р(x,y) - функция двух переменных
x и y, определенная на множестве М=М1хМ2 и принимающая значения из множества {1;0}.
Пример
Q(x, y) – “x=y” - предикат равенства на множестве RхR=R2
"Икс любит Игрека" -двухместный предикат.
Пример
Q(x, y) – “x=y” - предикат равенства на множестве RхR=R2
"Икс любит Игрека" -двухместный предикат.
Слайд 9
Определение
n-местный предикат - это функция определенная на наборах длины
n элементов некоторого множества M, принимающая значения в области True, False.
Множество М называется предметной областью предиката,
а x1, x2, ..xn –предметными переменными
Множество М называется предметной областью предиката,
а x1, x2, ..xn –предметными переменными
Слайд 10
Определение.
Предикат называется тождественно истинным (тождественно ложным), если на
всех наборах своих переменных принимает значение 1 (0), выполнимым, если на некотором наборе своих переменных принимает значение 1
Слайд 11
Логические операции над предикатами
Замечание
Предикаты при подстановки переменных становятся высказываниями, поэтому с
предикатами можно производить все логические операции
Для предикатов справедливы логические операции и две новые операции, специфические.
- операциями навешивания кванторов или операциями квантификации.
Эти операции соответствуют фразам
"для всех" - квантор общности и "некоторые" - квантор существования.
Выражение "существует точно одно Х такое, что..." - квантор существования и единственности
Для предикатов справедливы логические операции и две новые операции, специфические.
- операциями навешивания кванторов или операциями квантификации.
Эти операции соответствуют фразам
"для всех" - квантор общности и "некоторые" - квантор существования.
Выражение "существует точно одно Х такое, что..." - квантор существования и единственности
Слайд 12Пример (Экзюпери)
"Ты любишь потому, что ты любишь.
Не существует
причин, чтобы любить."
можно записать в виде:
можно записать в виде:
Слайд 13
Определение
Присоединение квантора с переменной к предикатной формуле называется
навешивание квантора на переменную х.
Переменная при этом называется связанной и вместо нее подставлять константы уже нельзя.
Если квантор навешивается на формулу с несколькими переменными, то он уменьшает число несвязанных переменных в этой формуле
Переменная при этом называется связанной и вместо нее подставлять константы уже нельзя.
Если квантор навешивается на формулу с несколькими переменными, то он уменьшает число несвязанных переменных в этой формуле
Слайд 14
Переменную х в предикате Р(х) называют свободной (ей можно придавать различные
значения из М),
в высказывании же х называют связанной квантором всеобщности.
в высказывании же х называют связанной квантором всеобщности.
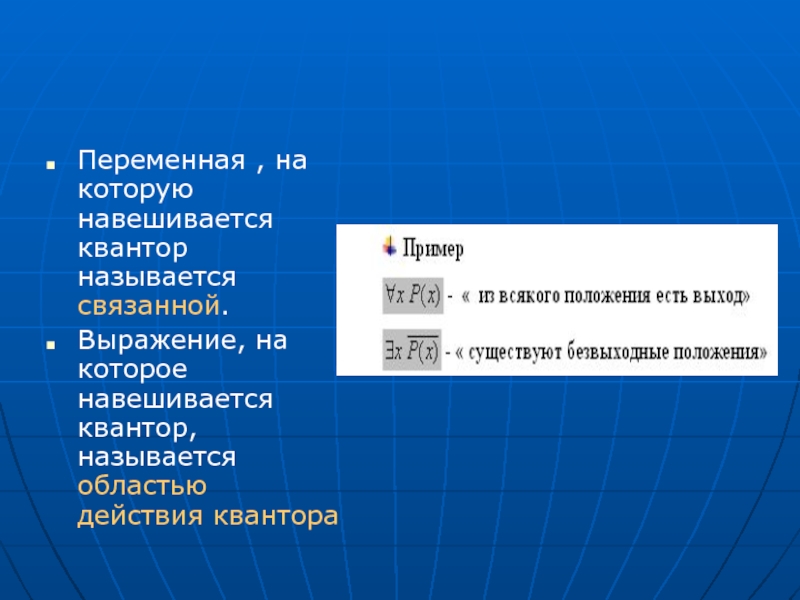
Слайд 15
Переменная , на которую навешивается квантор называется связанной.
Выражение, на которое навешивается
квантор, называется областью действия квантора
Слайд 16Пример
Предикат "ВСЕ любят кашу":
Возьмем отрицание
"НЕ ВЕРНО, что ВСЕ любят кашу".
Это равносильно (по закону Де Моргана!) заявлению:
"НЕКОТОРЫЕ НЕ любят кашу.
отрицание "задвинули" за квантор, в результате чего квантор сменился на противоположный
Слайд 17
Кванторы общности и существования называют двойственными относительно друг друга.
Вот некоторые
"классические примеры"несоответствия языка предикатов и естественного языка
Слайд 18Пример
предикат
"Собакам и кошкам вход воспрещен".
"ДЛЯ ВСЕХ иксов справедливо:
ЕСЛИ
икс - собака И икс - кошка, ТО иксу вход запрещен"
Ясно что таких иксов, которые бы были одновременно собакой и кошкой не существует! Как, впрочем, и таких игреков.
Поэтому ЕСЛИ икс - собака ИЛИ икс - кошка, ТО иксу вход запрещен"
Ясно что таких иксов, которые бы были одновременно собакой и кошкой не существует! Как, впрочем, и таких игреков.
Поэтому ЕСЛИ икс - собака ИЛИ икс - кошка, ТО иксу вход запрещен"
Слайд 21Свойства кванторов
1. Коммутативность одноименных кванторов
2.
Перестановка кванторов общности и существования меняет
смысл.
Слайд 23 Равносильные формулы логики предикатов
Определение
Две формулы логики предикатов А
и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.
Слайд 24Правила переноса кванторов через отрицание или
законы де Моргана для кванторов
Пусть
А(х) и В(х) – переменные предикаты, а С – переменное высказывание (или формула, не содержащая х).
Тогда имеют место равносильности
Тогда имеют место равносильности
Слайд 28
постоянное высказывание можно вносить под знак квантора всеобщности и выносить из
под знака в конъюнкции, дизъюнкции и импликации
Слайд 31 Нормальные формы формул логики предикатов
В логике предикатов формулы могут
иметь нормальную форму.
При этом, используя равносильности логики предикатов, каждую формулу логики предикатов можно привести к нормальной форме.
В логике предикатов различают два вида нормальных форм: приведенную и предваренную
При этом, используя равносильности логики предикатов, каждую формулу логики предикатов можно привести к нормальной форме.
В логике предикатов различают два вида нормальных форм: приведенную и предваренную
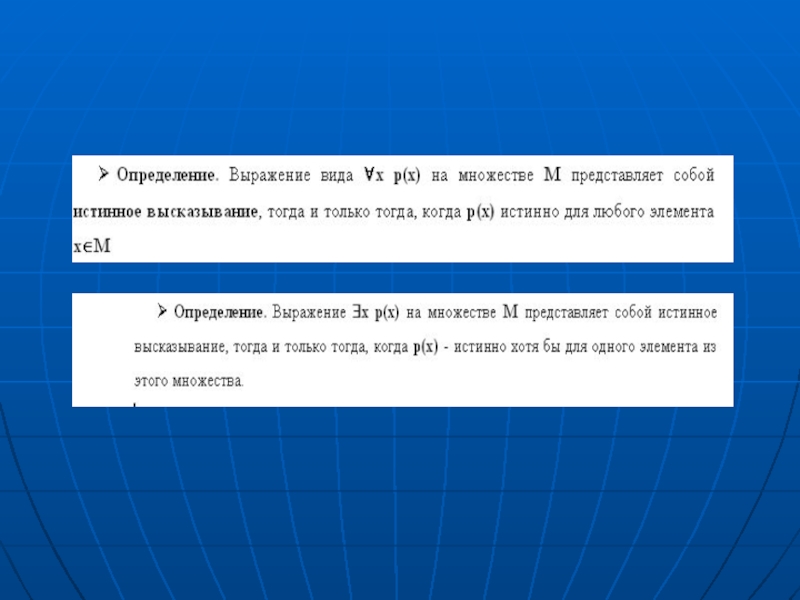
Слайд 32
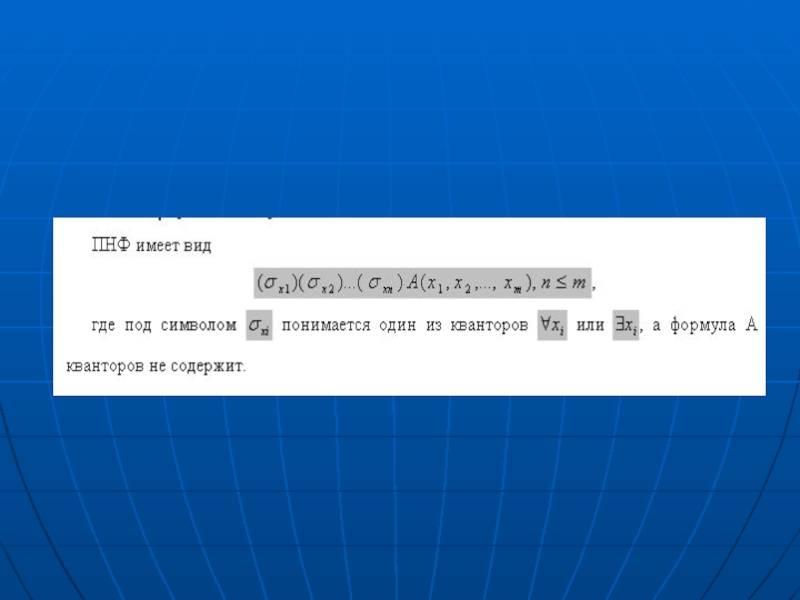
Среди нормальных форм формул логики предикатов выделяют так называемую предваренную (префиксную)
нормальную форму (ПНФ).
В ней кванторные операции
либо полностью отсутствуют,
либо они используются после всех операций алгебры логики
В ней кванторные операции
либо полностью отсутствуют,
либо они используются после всех операций алгебры логики
Слайд 35Алгоритм получения (приведения) ПНФ.
Формула B называется предваренной нормальной формой формулы
A ,
если она удовлетворяет ниже перечисленным требованиям:
1. Формулы А и B равносильны.
2. Формула B удовлетворяет следующим условиям:
а) используются логические операции ┐, v , & , при этом отрицание применяется только в атомарных формулах;
б) операции кванторов следуют за операциями алгебры ┐, v , &
если она удовлетворяет ниже перечисленным требованиям:
1. Формулы А и B равносильны.
2. Формула B удовлетворяет следующим условиям:
а) используются логические операции ┐, v , & , при этом отрицание применяется только в атомарных формулах;
б) операции кванторов следуют за операциями алгебры ┐, v , &
Слайд 36
Шаг 1. Исключить связки эквивалентности (~) и импликации (→).
Формула x
~ у заменяется на (x → у) & (x → у), а формула
A → B заменяется на (Ā v B).
Шаг 2. Переименовать, если необходимо, связанные переменные таким образом, чтобы никакая переменная не имела бы одновременно свободных и связанных вхождений. Это условие рассматривается и по отношению к подформулам.
A → B заменяется на (Ā v B).
Шаг 2. Переименовать, если необходимо, связанные переменные таким образом, чтобы никакая переменная не имела бы одновременно свободных и связанных вхождений. Это условие рассматривается и по отношению к подформулам.
Слайд 37
Шаг 3. Удалить те квантификации, область действия которых не содержит вхождений
квантифицированной переменной.
Шаг 4. Перенести отрицания внутри формулы в соответствия со следующими правилами:
Шаг 5. Перенести все квантификации в начало формулы
Шаг 4. Перенести отрицания внутри формулы в соответствия со следующими правилами:
Шаг 5. Перенести все квантификации в начало формулы
Слайд 39Скулемовские функции
Приведение формулы ЛП к сколемовской форме (сколемизация) призвано обеспечить
дальнейшее упрощение логических представлений и облегчить введение процедур машинной обработки в ЛП.
Отправной точкой сколемизации является предваренная нормальная форма, матрица которой приведена к конъюнктивной нормальной форме (КНФ).
Цель сколемизации - исключение Ǝ- квантификаций
Отправной точкой сколемизации является предваренная нормальная форма, матрица которой приведена к конъюнктивной нормальной форме (КНФ).
Цель сколемизации - исключение Ǝ- квантификаций
Слайд 40Алгоритм получения сколемовской формы
сопоставить каждой Ǝ- квантифицированной переменной список ∀- квантифицированных
переменных, предшествующих ей,
а также некоторую еще не использованную функциональную константу, число мест, у которой равно мощности списка.
Данная константа будет представлять сколемовскую функцию;
а также некоторую еще не использованную функциональную константу, число мест, у которой равно мощности списка.
Данная константа будет представлять сколемовскую функцию;
Слайд 41
4) в матрице формулы заменить каждое вхождение каждой Ǝ- квантифицированной переменной
на некоторый терм.
Этот терм является функциональной константой, соответствующей данной переменной и снабженной списком аргументов, также соответствующим той же самой переменной;
5) устранить из формулы все Ǝ - квантафикации.
Этот терм является функциональной константой, соответствующей данной переменной и снабженной списком аргументов, также соответствующим той же самой переменной;
5) устранить из формулы все Ǝ - квантафикации.
Слайд 42
Клаузальная форма -сколемовская форма, матрица которой приведена к КНФ.
Любая сколемовская
форма допускает эквивалентную клаузальную форму.