- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Lektsia_Tema_2 презентация
Содержание
- 1. Lektsia_Tema_2
- 2. Обыкновенные дифференциальные уравнения Дифференциальные уравнения в частных
- 3. Суть метода сеток заключается в покрытии расчетной
- 4. Построение разностной схемы конечно-разностная
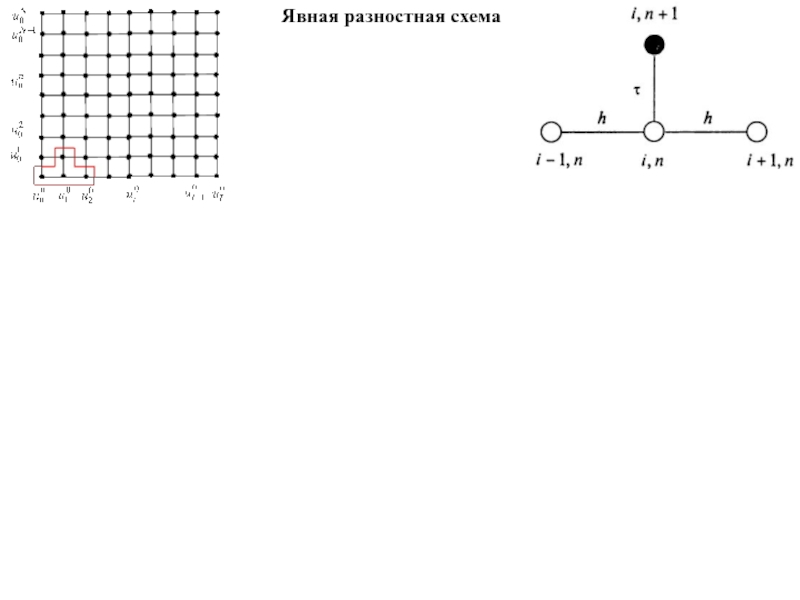
- 5. Явная разностная схема
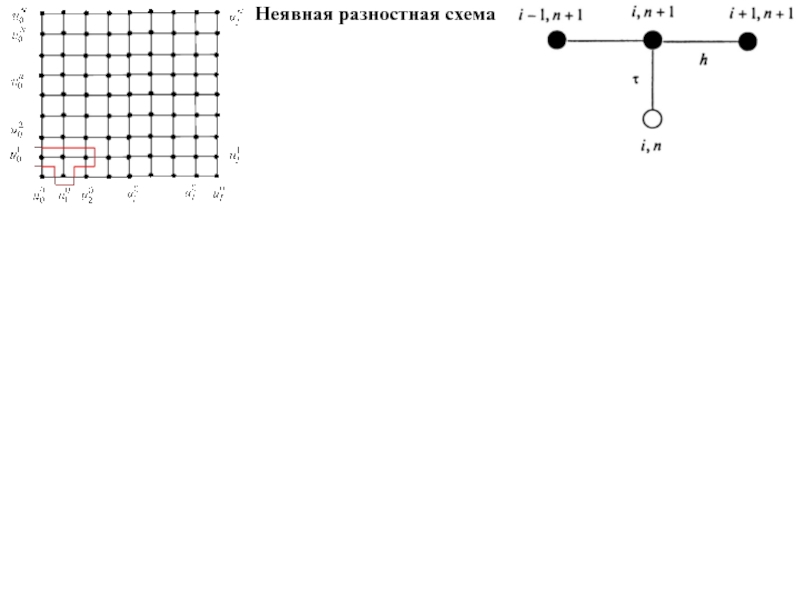
- 6. Неявная разностная схема
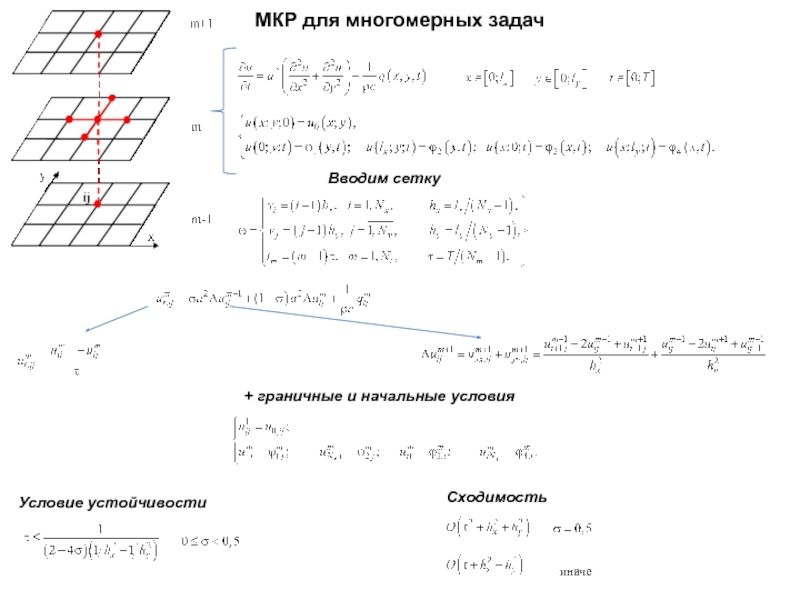
- 7. МКР для многомерных задач
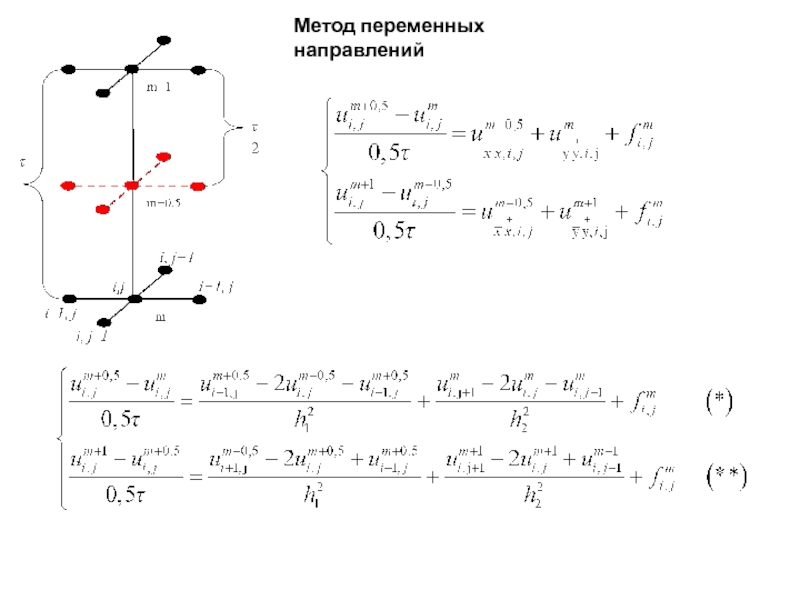
- 8. Метод переменных направлений
Слайд 1Лекция Вычислительная механика
Аппроксимация дифференциальных операторов
К.т.н., доцент каф. ВМиМ
Каменских Анна Александровна
239-15-64
Слайд 2Обыкновенные дифференциальные уравнения
Дифференциальные уравнения в частных производных
- задачи химической кинетики,
-
движение систем взаимодействующих
материальных точек
- и другие задачи физики, химии, техники
задачи математической физики,
гидродинамики,
акустики
и других областей знаний.
Решение дифференциальных уравнений
аналитические
численные
- точные – методы позволяют выразить решение дифференциальных уравнений через элементарные функции (в аналитическом виде);
- приближенные – методы, в которых решение получается как предел некоторой последовательности, члены которой выражаются через элементарные функции.
-численные методы не позволяют найти точное решение дифференциальных уравнений в аналитической форме. С их помощью получается таблица приближенных (иногда точных) значений искомого решения в некоторых точках рассматриваемой области решения, именуемых сеткой. В силу этого численные методы называют иначе разностными методами или методами сеток.
Слайд 3Суть метода сеток заключается в покрытии расчетной области (x,t) сеткой из
Сеткой определяются узлы, в которых будет осуществляться поиск решения.
Далее необходимо заменить дифференциальные уравнения в частных производных (уравнение диффузии, уравнение теплопроводности и др.) аппроксимирующими их уравнениями в конечных разностях, выписав соответствующие разностные уравнения для каждого (i,n)-гo узла сетки.
Понятие разностной схемы
Совокупность разностных уравнений, построенных на сетке и аппроксимирующих основное дифференциальное уравнение на V и краевые условия на Г, называется разностной схемой.
Таким образом, вместо поиска непрерывных зависимостей u(x) реализация разностной схемы позволяет отыскать значения функции в узлах сетки. Ее поведение в промежутках между узлами может быть получено при помощи построения какой-либо интерполяции.
конечные разности на сетке
Слайд 4Построение разностной схемы
конечно-разностная схема
Конечно-разностная схема называется устойчивой, если малым изменениям входных
Если р.с. устойчива и аппроксимирует исходную краевую задачу с порядком n, то она сходиться, причем скорость сходимости равна порядку аппроксимации.