- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КВАДРАТНЫЕ УРАВНЕНИЯ презентация
Содержание
- 1. КВАДРАТНЫЕ УРАВНЕНИЯ
- 2. ЦЕЛЬ: НАУЧИТЬСЯ РЕШАТЬ КВАДРАТНЫЕ
- 3. Определение 1 Квадратным называют уравнение вида
- 4. Определение 2. Квадратное уравнение называют приведенным, если
- 5. Задание. Распределите данные уравнения на четыре группы
- 6. 1 группа 9х2 – 6х + 10
- 7. Полное квадратное уравнение ах2 + bx +
Слайд 1КВАДРАТНЫЕ УРАВНЕНИЯ
Основные понятия, связанные с квадратными уравнениями
Лебедева Е.В., учитель математики
МБОУ
Слайд 2ЦЕЛЬ:
НАУЧИТЬСЯ РЕШАТЬ КВАДРАТНЫЕ
УРАВНЕНИЯ РАЗНЫМИ
ЗАДАЧИ:
Сформулировать определения:
квадратного уравнения;
приведенного и неприведенного квадратных
уравнений;
корня квадратного уравнения.
Ввести новые понятия:
коэффициенты квадратного уравнения;
полные и неполные квадратные уравнения.
3. Рассмотреть теорию решения неполных и полных квадратных уравнений.
Слайд 3Определение 1 Квадратным называют уравнение вида ах2 + bx + c =
Задание.
Из данных уравнений выберите квадратные:
а) х2 – 4 = 0; б) х3 +3х – 1 = 0; в)
г) 8х = 0; д) 2х2 – 5х + 6 = 0; е) 8х – х2 + 5 = 0.
Слайд 4Определение 2. Квадратное уравнение называют приведенным, если старший коэффициент равен 1;
Определение 3.
Корнем квадратного уравнения
ах2 + bx + c = 0 называют всякое значение переменной х, при котором квадратный трехчлен ах2 + bx + c обращается в нуль; такое значение переменной х также называют корнем квадратного трехчлена.
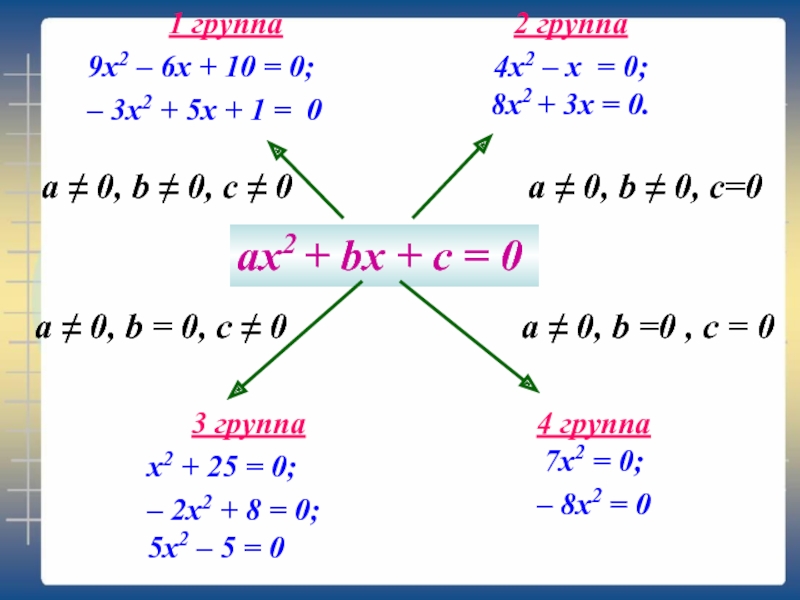
Слайд 5Задание. Распределите данные уравнения на четыре группы и объясните, по какому
вы это сделали.
а) 9х2 - 6х + 10 = 0;
б) 4х2 – х = 0;
в) 7х2 = 0;
г) х2 + 25 = 0;
в) – 3х2 + 5х + 1 = 0;
е) – 2х2 + 8 = 0;
ж) 5х2 – 5 = 0;
з) – 8x2 = 0;
и) 8х2 + 3х = 0.
Слайд 61 группа
9х2 – 6х + 10 = 0;
– 3х2 + 5х
2 группа
4х2 – х = 0;
8х2 + 3х = 0.
3 группа
х2 + 25 = 0;
– 2х2 + 8 = 0;
5х2 – 5 = 0
4 группа
7х2 = 0;
– 8x2 = 0
ах2 + bx + c = 0
a ≠ 0, b ≠ 0, c ≠ 0
a ≠ 0, b =0 , c = 0
a ≠ 0, b = 0, c ≠ 0
a ≠ 0, b ≠ 0, c=0
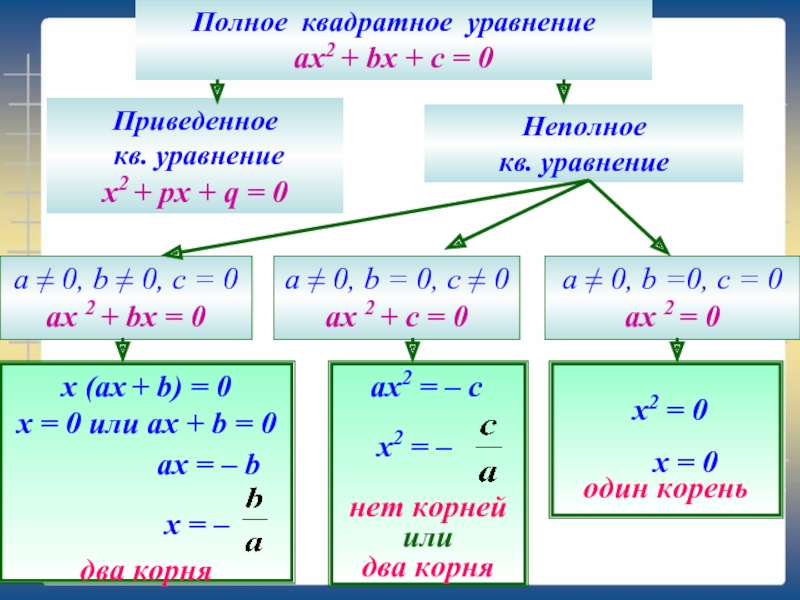
Слайд 7Полное квадратное уравнение
ах2 + bx + c = 0
Приведенное
кв. уравнение
х2
Неполное
кв. уравнение
a ≠ 0, b =0, c = 0
ах 2 = 0
a ≠ 0, b = 0, c ≠ 0
ах 2 + c = 0
a ≠ 0, b ≠ 0, c = 0
ах 2 + bx = 0
x (ах + b) = 0
х = 0 или ах + b = 0
ах = – b
x = –
два корня
ах2 = – c
x2 = –
нет корней
или
два корня
х2 = 0
x = 0
один корень