- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Квадратичная функция и её график
Содержание
- 1. Квадратичная функция и её график
- 2. Определение Квадратичной функцией называется функция, которую
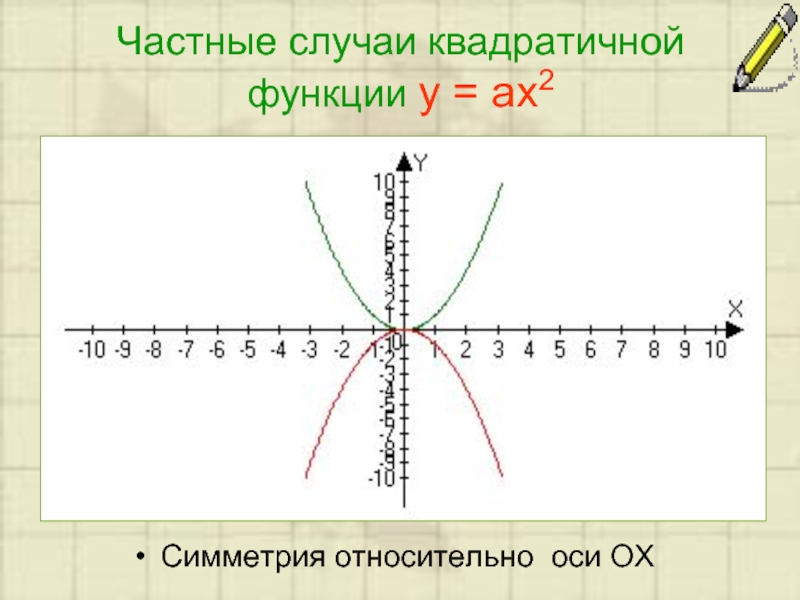
- 3. Частные случаи квадратичной функции y = ax2 Симметрия относительно оси ОХ
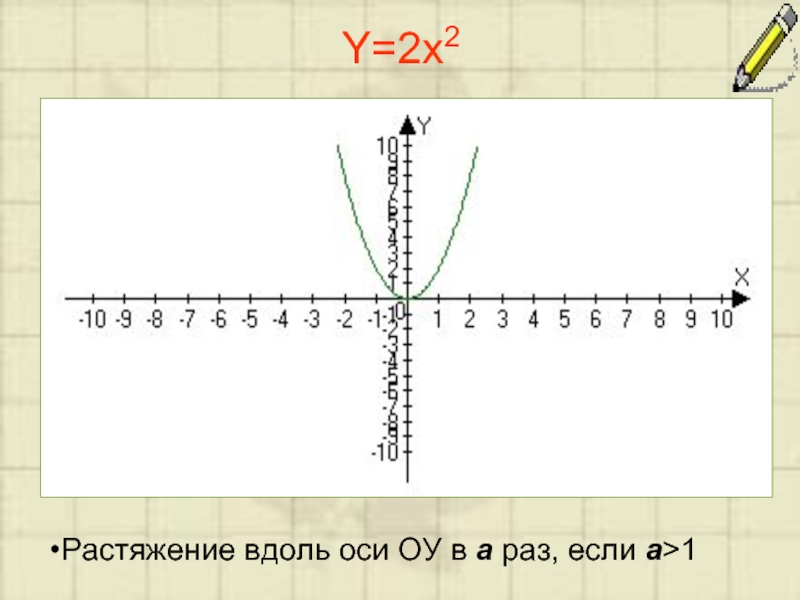
- 4. Y=2x2 Растяжение вдоль оси ОУ в a раз, если a>1
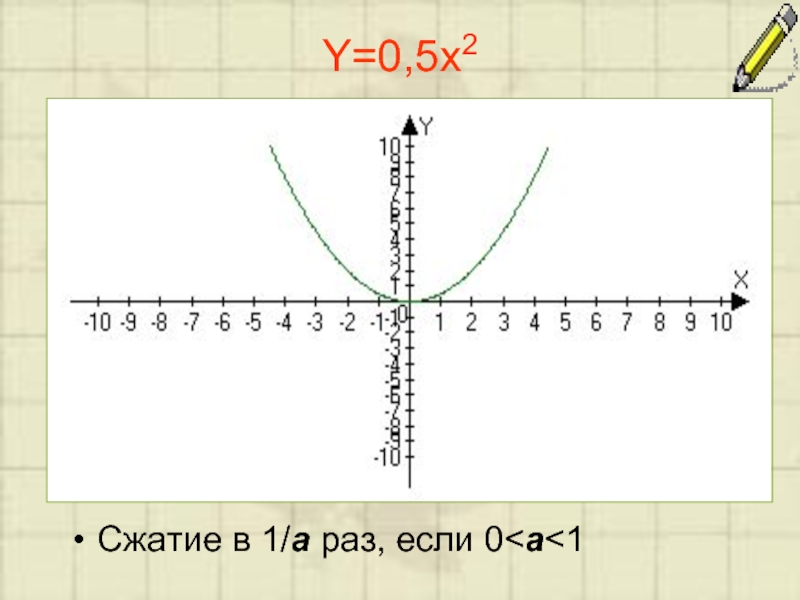
- 5. Y=0,5x2 Сжатие в 1/a раз, если 0
- 6. Графики функций у=ах2+n Сдвиг вдоль оси ОУ на
- 7. Графики функций у = а(х-m)2 Сдвиг вдоль оси
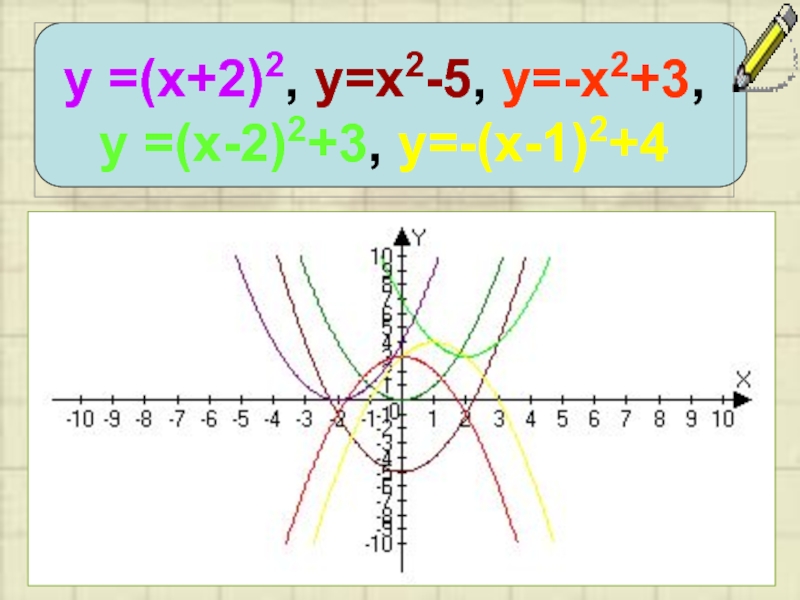
- 8. у =(х+2)2, у=х2-5, у=-х2+3, у =(х-2)2+3, у=-(х-1)2+4
- 9. Построение графика квадратичной функции у=ах2+bx+c Определить направление ветвей
- 10. Желаю успехов в изучении темы.
- 11. Скачать презентацию
Определение Квадратичной функцией называется функция, которую можно задать формулой вида y=ax2+bx+c, где x-независимая переменная, a, b и c-некоторые числа, причём a=0. Графиком является парабола.
Слайды и текст этой презентации
Слайд 2Определение
Квадратичной функцией называется функция, которую
можно задать формулой вида y=ax2+bx+c, где x-независимая
переменная, a, b и c-некоторые числа, причём a=0.Графиком является парабола.
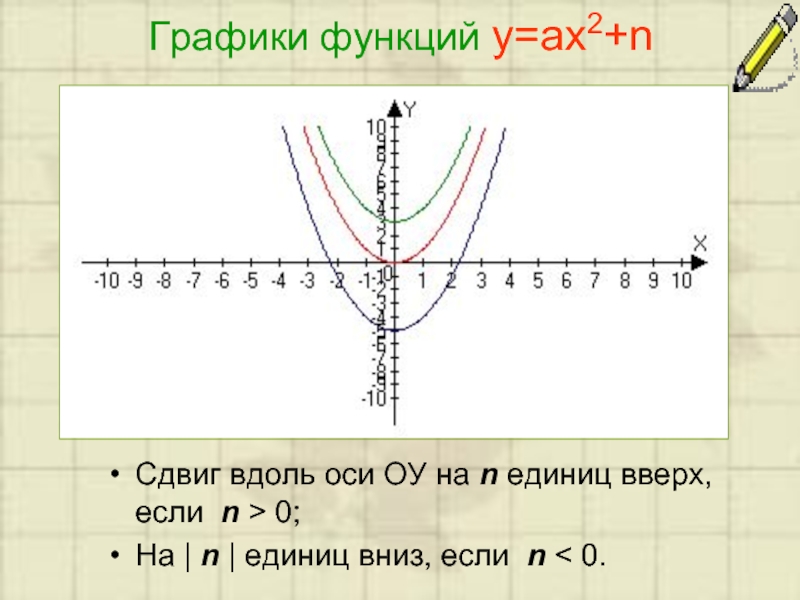
Слайд 6Графики функций у=ах2+n
Сдвиг вдоль оси ОУ на
n единиц вверх, если n > 0;
На
| n | единиц вниз, если n < 0.
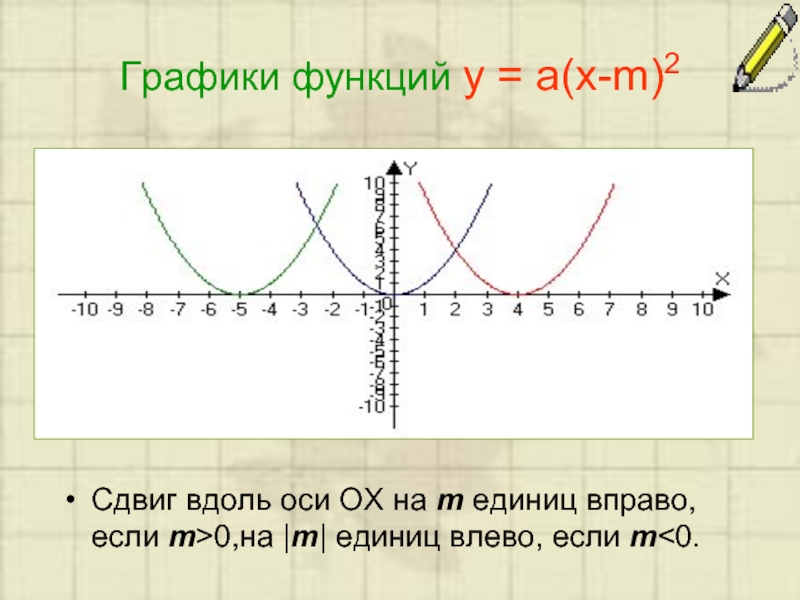
Слайд 7Графики функций у = а(х-m)2
Сдвиг вдоль оси
ОХ на m единиц вправо, если m>0,на
|m| единиц влево, если m<0.
Слайд 9Построение графика квадратичной функции у=ах2+bx+c
Определить направление ветвей
параболы.
Если а>0,ветви параболы направлены вверх.
Если а
параболы направлены вниз.2. Найти координаты вершины параболы А(m ; n).
m= -b / 2a , n= y (m)
3. Написать уравнение оси симметрии х =m.
4. Составить таблицу дополнительных значений с учётом оси симметрии.
