и спектрами сигналов
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Корреляционный анализ презентация
Содержание
- 1. Корреляционный анализ
- 2. Автокорреляционные функции сигналов Корреляционная функция
- 3. АКФ сигнала с конечной энергией
- 4. Свойства автокорреляционной функции -Т
- 5. АКФ периодического сигнала Периодический сигнал
- 6. Взаимнокорреляционные функции сигналов Отличается от
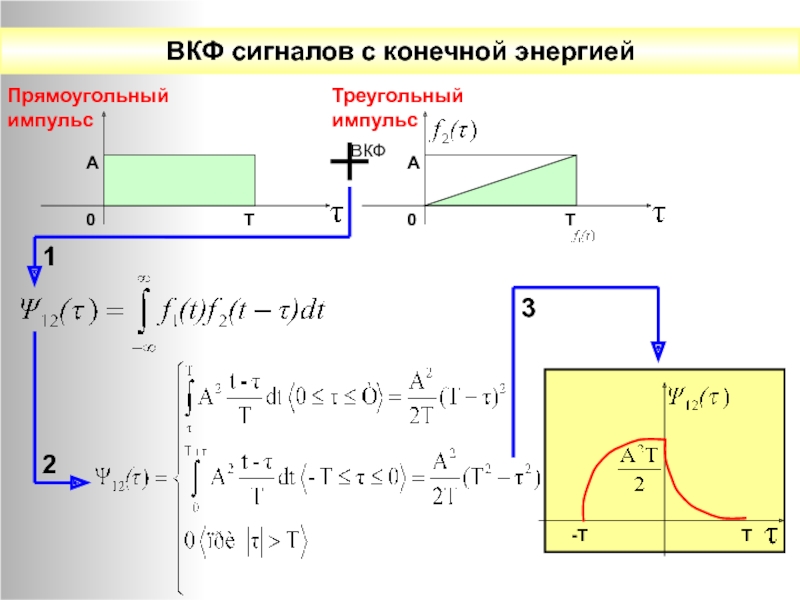
- 7. ВКФ сигналов с конечной энергией
- 8. Свойства ВКФ сигналов с конечной
- 9. Связь между КФ и спектрами
Слайд 1
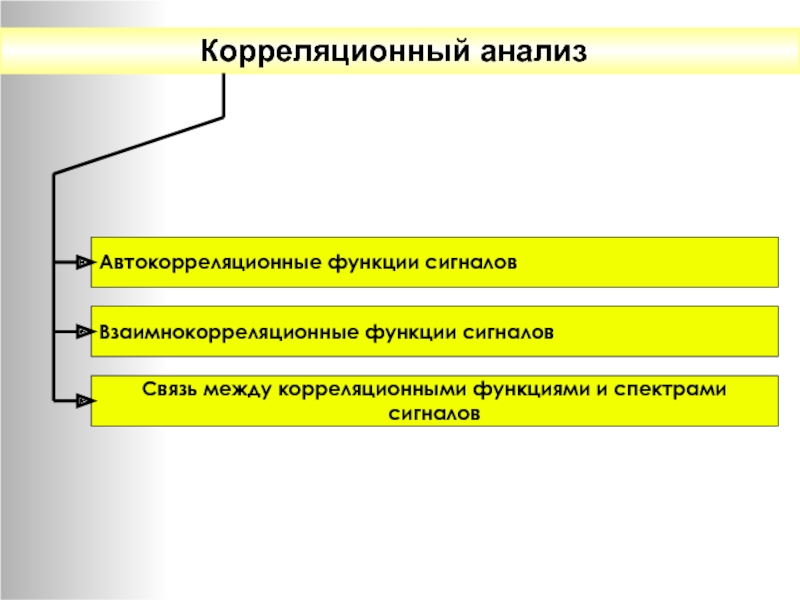
Корреляционный анализ
Автокорреляционные функции сигналов
Взаимнокорреляционные функции сигналов
Связь между корреляционными функциями
Слайд 2
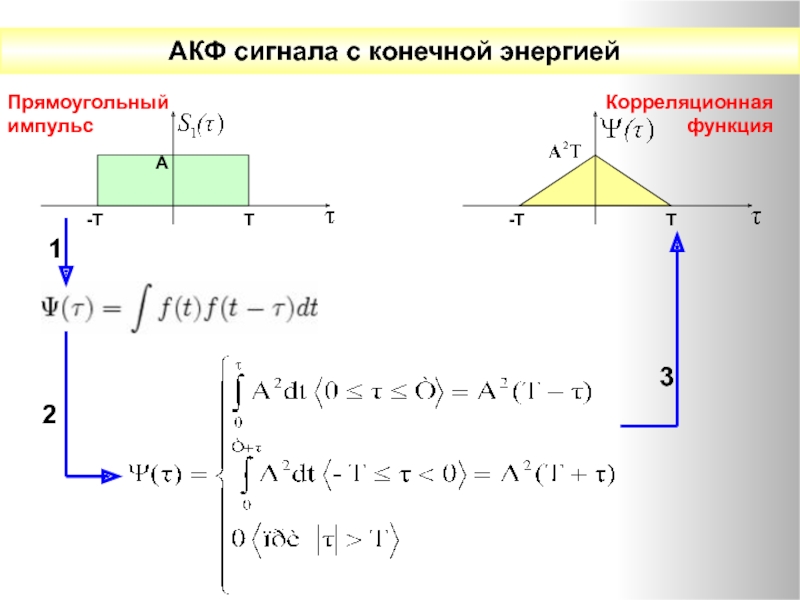
Автокорреляционные функции сигналов
Корреляционная функция детерминированного сигнала с конечной энергией есть интеграл
от произведения двух копий сигнала, сдвинутых друг относительно друга на время т
Слайд 4
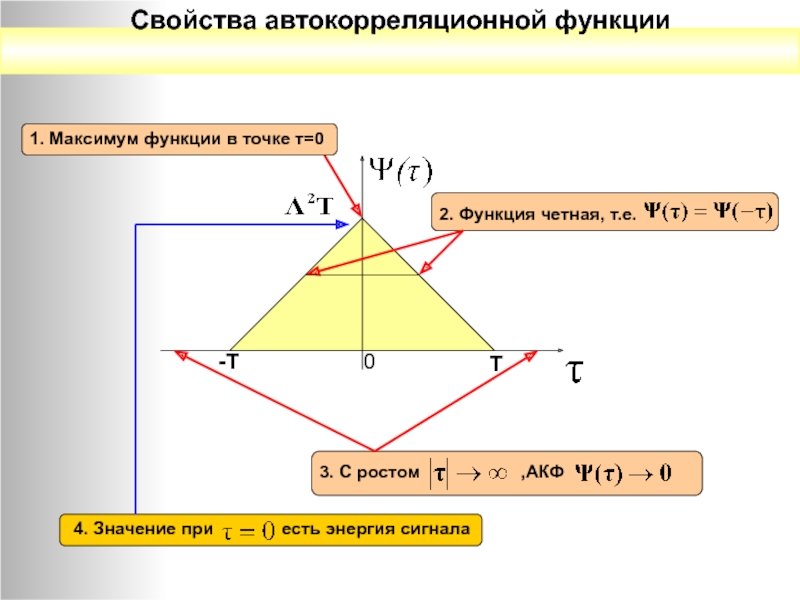
Свойства автокорреляционной функции
-Т
Т
0
1. Максимум функции в точке т=0
2. Функция четная, т.е.
3. С ростом
,АКФ
4. Значение при
есть энергия сигнала
Слайд 5
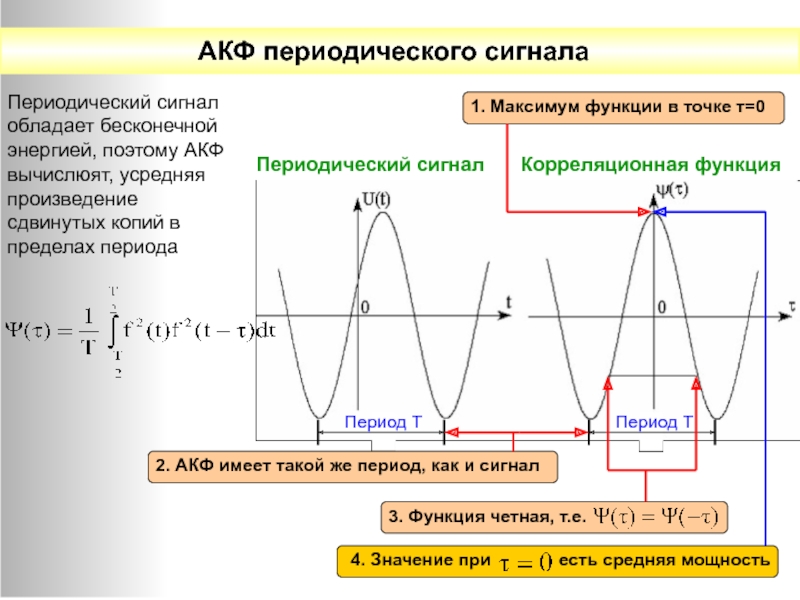
АКФ периодического сигнала
Периодический сигнал
Корреляционная функция
Период Т
Периодический сигнал обладает бесконечной энергией, поэтому
АКФ вычислюят, усредняя произведение сдвинутых копий в пределах периода
Период Т
3. Функция четная, т.е.
2. АКФ имеет такой же период, как и сигнал
1. Максимум функции в точке т=0
4. Значение при
есть средняя мощность
Слайд 6
Взаимнокорреляционные функции сигналов
Отличается от АКФ тем, что для ВКФ коррелируются
два различных
сигнала
(т.е. АКФ – частный случай ВКФ).
(т.е. АКФ – частный случай ВКФ).
Для периодических сигналов ВКФ практически не применяется.
Однако, применение ВКФ в таких случаях возможно лишь при одинаковых периодах сигналов
Слайд 8
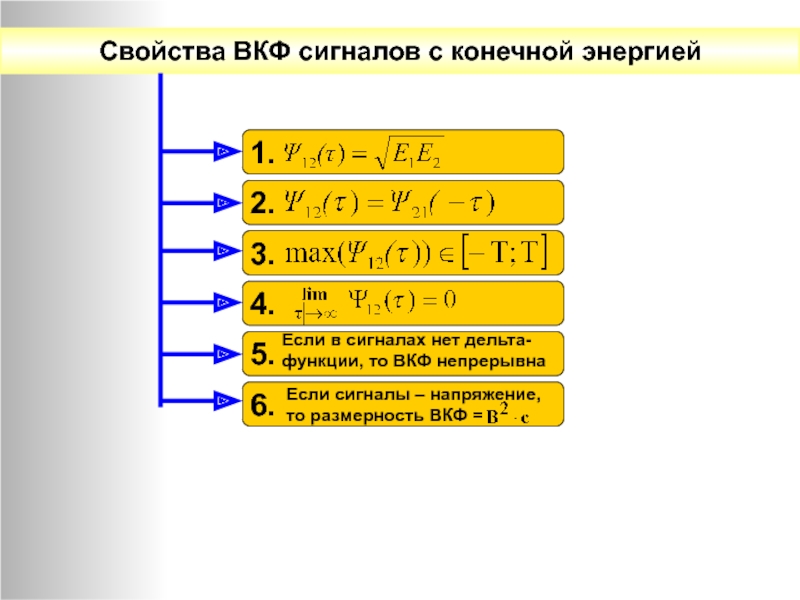
Свойства ВКФ сигналов с конечной энергией
1.
2.
3.
4.
5.
6.
Если в сигналах нет дельта-функции, то
ВКФ непрерывна
Если сигналы – напряжение,
то размерность ВКФ =
Слайд 9
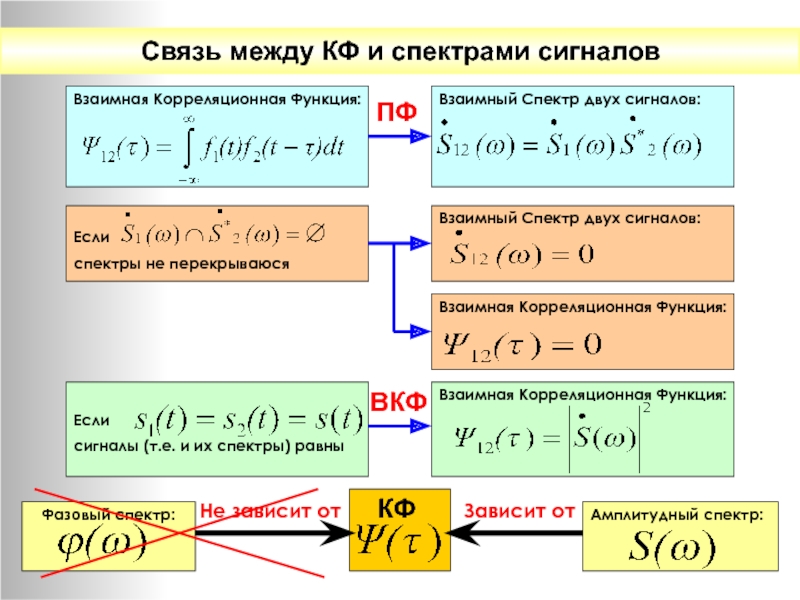
Связь между КФ и спектрами сигналов
Взаимная Корреляционная Функция:
ПФ
Взаимный Спектр двух сигналов:
Если
спектры
не перекрываюся
Взаимный Спектр двух сигналов:
Взаимная Корреляционная Функция:
ВКФ
Если
сигналы (т.е. и их спектры) равны
Взаимная Корреляционная Функция:
КФ
Фазовый спектр:
Амплитудный спектр:
Зависит от
Не зависит от
