- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Компьютерное моделирование презентация
Содержание
- 1. Компьютерное моделирование
- 2. Моделирование – замена одного объекта (процесса или
- 3. Наиболее распространенные виды классификации моделей,
- 5. Классификация моделей по способу представления Материальные
- 6. Информационная модель – модель, представляющая объект, процесс
- 7. Этапы построения информационной модели: Выделение существенных
- 8. Хорошо поставленная задача – задача, для которой
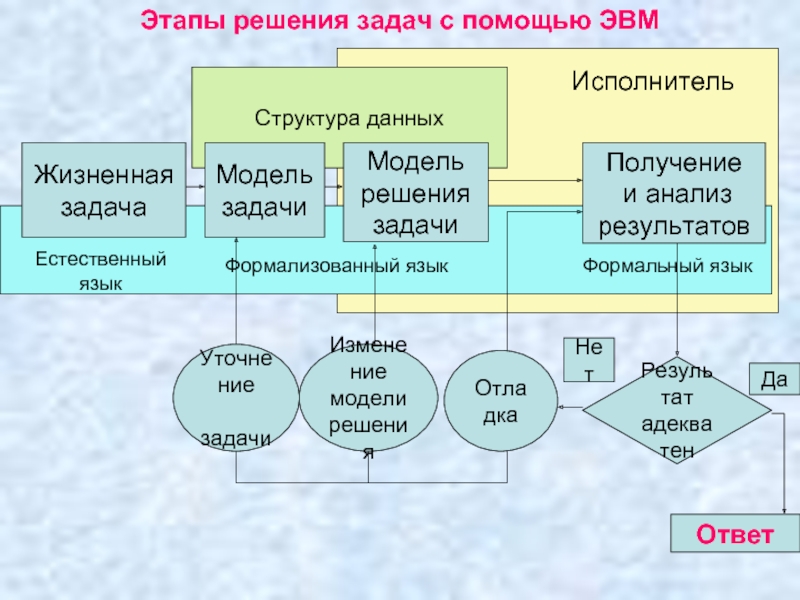
- 9. Этапы решения задач на ЭВМ: Математическая модель:
- 10. Укажите, какие модели вы обычно используете для
- 11. Какие модели являются имитационными, какие – информационными,
- 12. Системный подход и информационные модели
- 13. Назовите систему, представленную каждым графом? Ответ: Стол,
- 14. №2. Могут ли разные явления описываться одной
- 15. Классификация моделей по фактору времени Внутреннее устройство
- 16. Динамические модели и черные ящики Черный ящик
- 17. Укажите, какие модели являются статическими, а какие динамическими? + + + + + + +
- 18. Л/работа «Модель неограниченного роста (НОР)» В
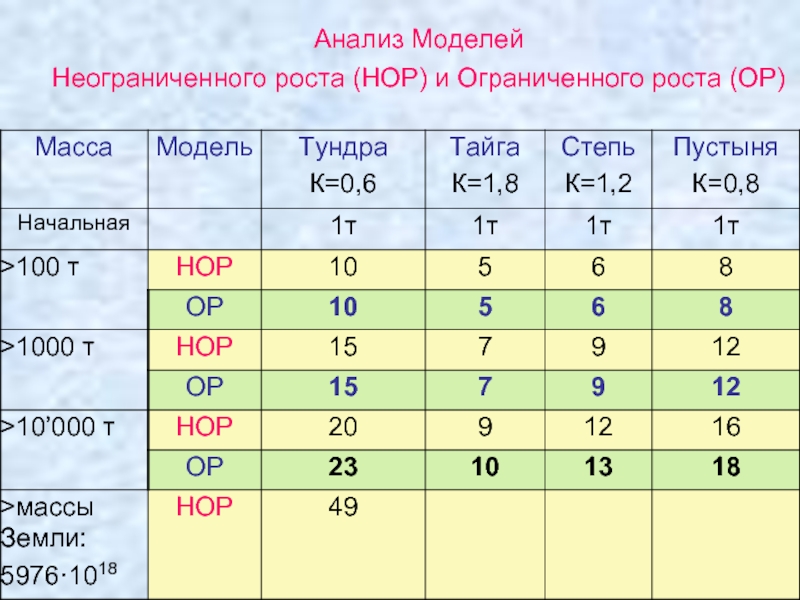
- 19. Анализ Моделей Неограниченного роста (НОР) и Ограниченного роста (ОР)
- 20. Анализ Моделей Неограниченного роста (НОР) и Ограниченного роста (ОР)
- 21. Выводы: I.Модель неограниченного роста (НОР) На увеличение
- 22. Л/работа «Модель ограниченного роста (ОР)» Построение модели
- 23. Анализ Моделей Неограниченного роста (НОР) и Ограниченного роста (ОР)
- 24. Выводы: I.Модель ограниченного роста (ОР) На начальных
- 25. Адекватность модели Если модель дает удовлетворительные результаты
- 26. Что значит найти границы адекватности данной модели?
- 27. Неадекватность модели может проявляться: В несоответствии результатов,
- 28. Л/работа «Поиск границ адекватности модели» Цель: исследовать
- 29. Модель неограниченного роста Параметры модели
- 30. Зависимость границы адекватности n от k и
- 31. Решая показательное неравенство L ≥ 8(1+k)n-1 ,
- 32. Этапы решения задач с помощью ЭВМ Результат адекватен
- 33. Компьютерные модели в задачах управления
- 34. Модель потребления возобновляемых ресурсов Целенаправленное воздействие на
- 35. Л/работа «Управление добычей возобновляемых ресурсов» Построение модели
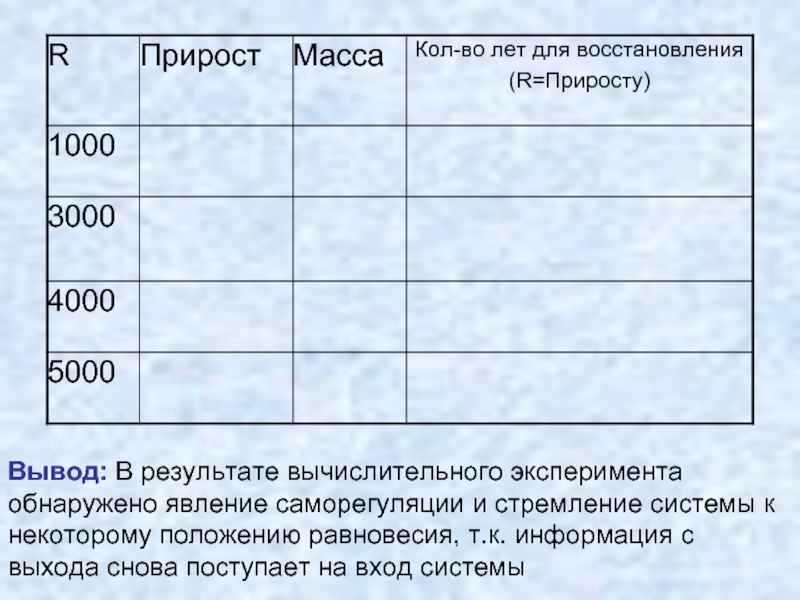
- 36. Вывод: В результате вычислительного эксперимента обнаружено явление
Слайд 2Моделирование – замена одного объекта (процесса или явления) другим, но сохраняющим
(процесса или явления)
Модель – аналог (заменитель) оригинала, отражающий некоторые его характеристики
Модельное представление – единственный способ мыслительной обработки воспринимаемой человеком окружающей действительности
Цель моделирования не в стремлении упростить изучаемый объект (процесс или явление), а в представлении его в такой форме, чтобы для исследования интересующего объекта можно было применить имеющийся у человека инструментарий.
Слайд 3
Наиболее распространенные
виды классификации моделей,
определяемых следующими признаками:
областью использования;
учетом в модели
способом представления моделей;
областью знаний (биологические, экономические социологические, исторические и т.п)
множество других факторов
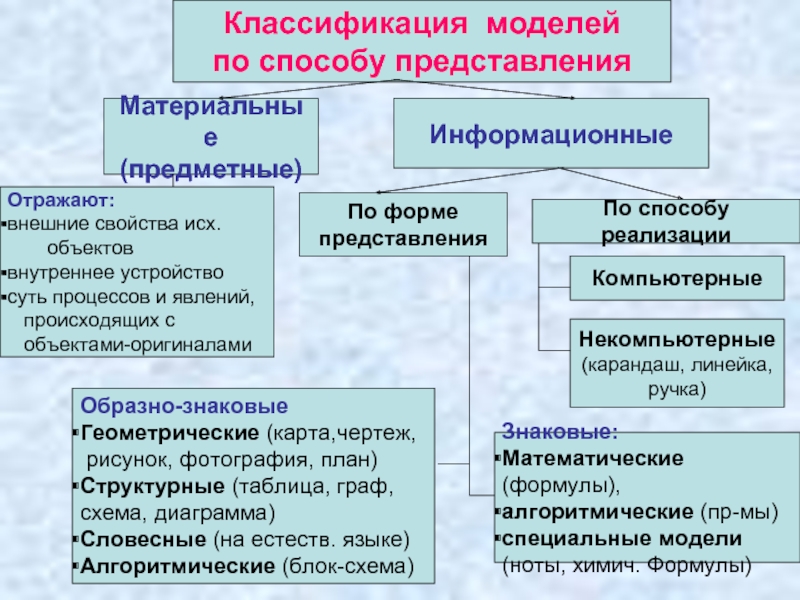
Слайд 5Классификация моделей
по способу представления
Материальные
(предметные)
Информационные
Компьютерные
Некомпьютерные
(карандаш, линейка,
ручка)
По способу реализации
По форме
представления
Образно-знаковые
Геометрические
рисунок, фотография, план)
Структурные (таблица, граф,
схема, диаграмма)
Словесные (на естеств. языке)
Алгоритмические (блок-схема)
Знаковые:
Математические (формулы),
алгоритмические (пр-мы)
специальные модели
(ноты, химич. Формулы)
Отражают:
внешние свойства исх.
объектов
внутреннее устройство
суть процессов и явлений,
происходящих с
объектами-оригиналами
Слайд 6Информационная модель – модель, представляющая объект, процесс или явление набором параметров
Математическая модель – информационная модель, в которой параметры и зависимости между ними выражены в математической форме.
Компьютер – инструмент решения задач на основе информационных моделей
Слайд 7Этапы построения
информационной модели:
Выделение существенных факторов для построения модели
Формализация - описание
Установка связей между параметрами и их описание
Слайд 8Хорошо поставленная задача – задача, для которой построена модель, учитывающая существенные
Плохо поставленная задача – для которой неизвестно заранее, какие факторы существенны, не выявлены параметры или не указаны связи между ними (т.е. не построена модель)
Слайд 9Этапы решения задач на ЭВМ:
Математическая модель:
1. предположения, на которых основана модель
2. Формализация (описание факторов с помощью параметров)
3. Математическое описание, связь (формулы, уравнения, неравенства)
II. Алгоритм
III. Программа
IV. Получение и анализ результатов:
1. ввод и отладка программы
2. Тестирование:
проверка основных частных случаев исходных данных
проверка граничных случаев
проверка недопустимых случаев исходных данных
Слайд 10Укажите, какие модели вы обычно используете для решения следующих жизненных задач
Существенно содержание фильма или место расположения кинотеатра
Купить билет в кино
2) Расписание сеансов
Существенен фактор времени
3) План расположения мест в кинотеатре и указатель цен на них.
Фактор комфорта или финансовых ограничений
Рецепт приготовления торта
(алгоритм)
Норма и порядок смешивания компонентов
1) Афиша с информацией о том, какие фильмы и в каких кинотеатрах идут
Испечь торт
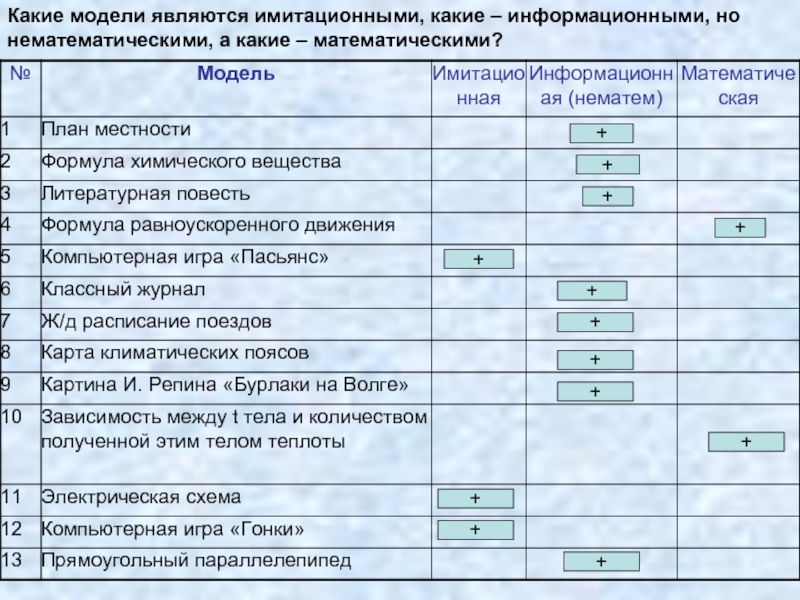
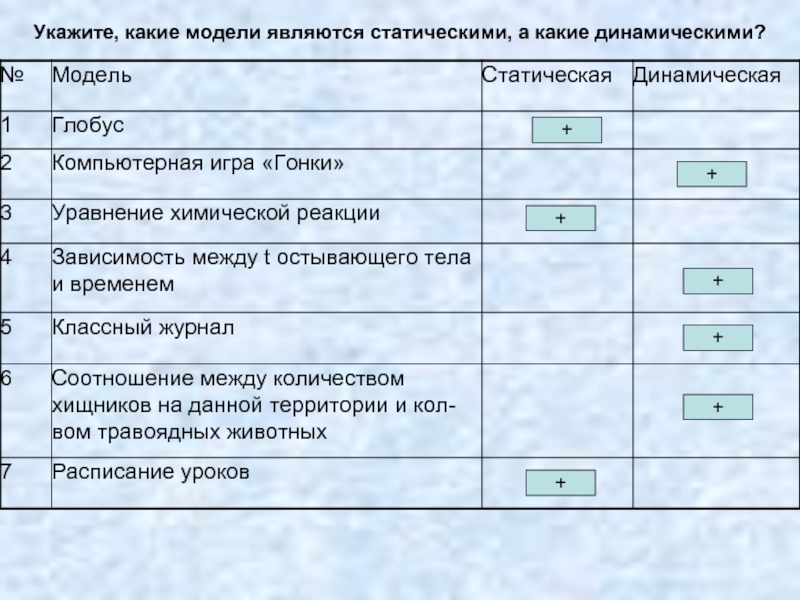
Слайд 11Какие модели являются имитационными, какие – информационными, но нематематическими, а какие
+
+
+
+
+
+
+
+
+
+
+
+
+
Слайд 12
Системный подход и информационные модели
Системный подход к построению моделей был предложен
Система – модель, представляющая собой некоторую совокупность элементов и связей между ними.
Совокупность отношений, которыми наделена система, называют структурой этой системы.
Связи элементов создают систему только тогда, когда в результате этих связей образуется новый целостный объект, обладающий такими свойствами, которые без этих связей не были присущи совокупности данных элементов. Появление таких свойств называют системным эффектом.
Системный подход – общие методы построения системных моделей
Всякая информационная модель является системной.
Не всякая системная модель является информационной (натуральные модели: скелет, самолет, авто. Т.к нет никаких параметров, описывающих действие каких-либо факторов)
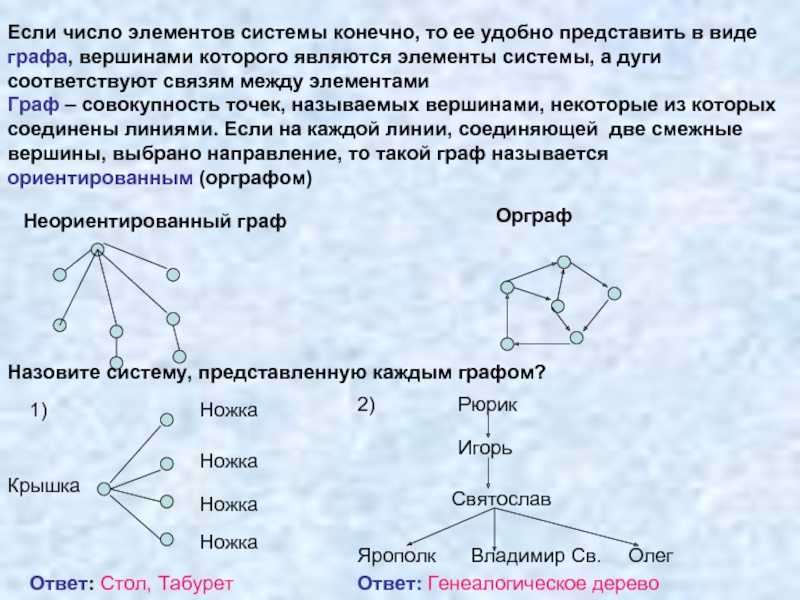
Слайд 13Назовите систему, представленную каждым графом?
Ответ: Стол, Табурет
Ответ: Генеалогическое дерево
Если число элементов
Граф – совокупность точек, называемых вершинами, некоторые из которых соединены линиями. Если на каждой линии, соединяющей две смежные вершины, выбрано направление, то такой граф называется ориентированным (орграфом)
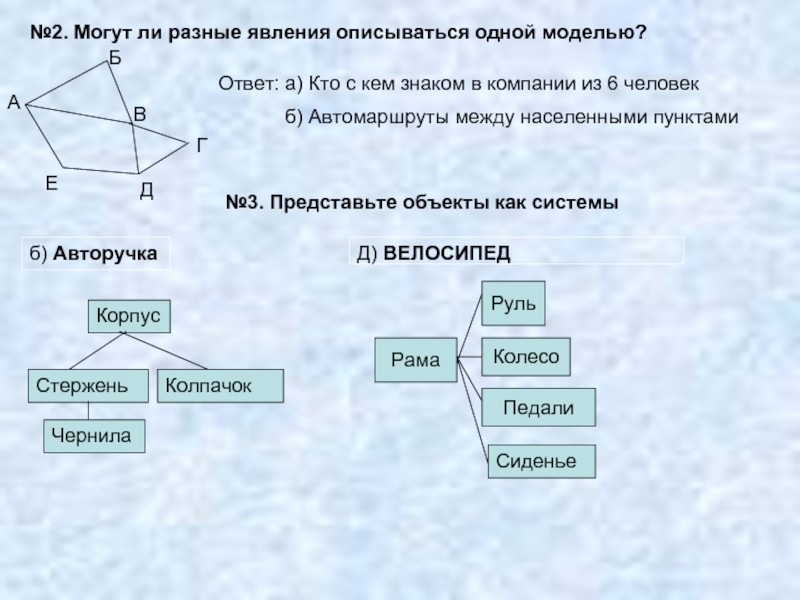
Слайд 14№2. Могут ли разные явления описываться одной моделью?
Ответ: а) Кто с
б) Автомаршруты между населенными пунктами
№3. Представьте объекты как системы
б) Авторучка
Д) ВЕЛОСИПЕД
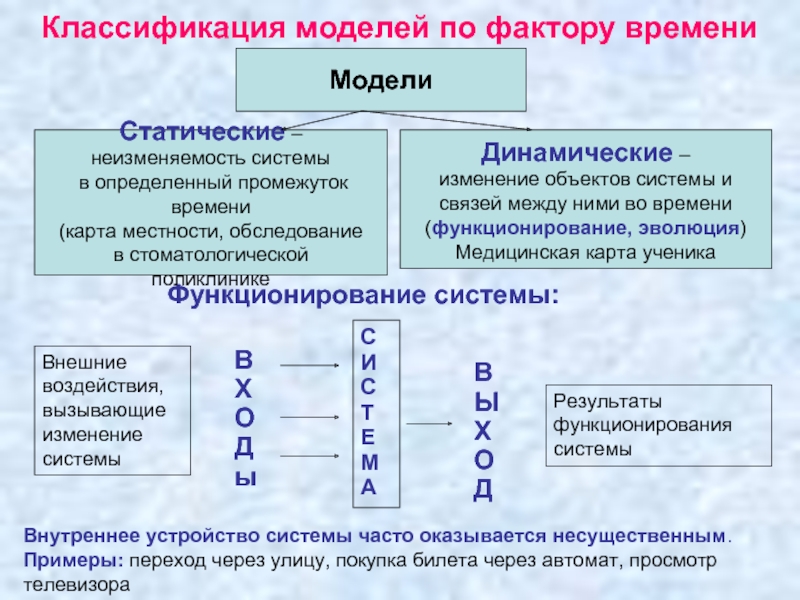
Слайд 15Классификация моделей по фактору времени
Внутреннее устройство системы часто оказывается несущественным. Примеры:
Слайд 16Динамические модели и черные ящики
Черный ящик – объект, внутренне устройство которого
Используется как средство моделирования поведения тех или иных объектов, т.к. не зная как устроен Черный ящик, мы можем лишь предполагать, какую информацию он воспримет на ВХОДАХ и какой будет его реакция на те или иные входные сигналы. Догадку можно проверить, подавая на входы ту или иную информацию и наблюдая на выходах за реакцией черного ящика на эту информацию.
Если догадка будет регулярно подтверждаться, то можно считать, что мы построили модель той динамической системы, которая представлена данным черным ящиком.
Кибернетика – наука, изучающая процессы управления в живой природе и системах, созданных человеком, а также разрабатывает методы построения эффективного управления при решении человеком тех или иных жизненных задач
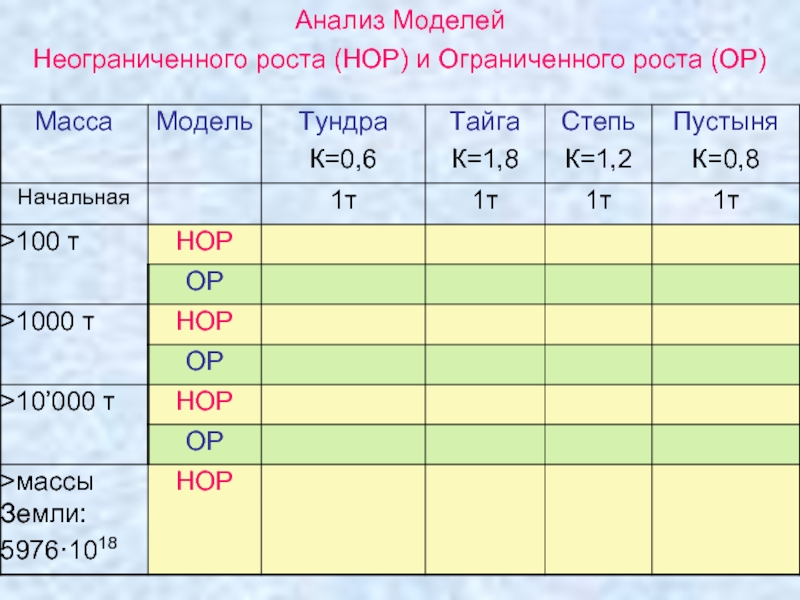
Слайд 18Л/работа «Модель неограниченного роста (НОР)»
В 1937 г. На остров Протекшен
Как меняется масса растений в различных природных зонах (тундра, тайга, степь, пустыня)?
Построение модели
Существенные факторы:
Прирост массы живых организмов за единицу времени пропорционален уже имеющейся массе.
Рассмотрим воздействие окружающей среды на численность популяции живых организмов как черный ящик.
2. Формализация. Дано:
М(0) – начальное кол-во живых организмов
K – коэффициент прироста за год
Найти: M(n) –число живых организмов через n лет
3. Связь: M(n+1) - M(n) – прирост за 1 год, тогда M(n+1) - M(n) = kM(n)
M(n+1) = M(n) + kM(n) или M(n+1) = (1 +k)·M(n)
Обнаруженную закономерность можно сформулировать так: если действие окружающей среды сказывается лишь на скорости прироста, то живые организмы размножаются в геометрической прогрессии.
Это модель неограниченного роста
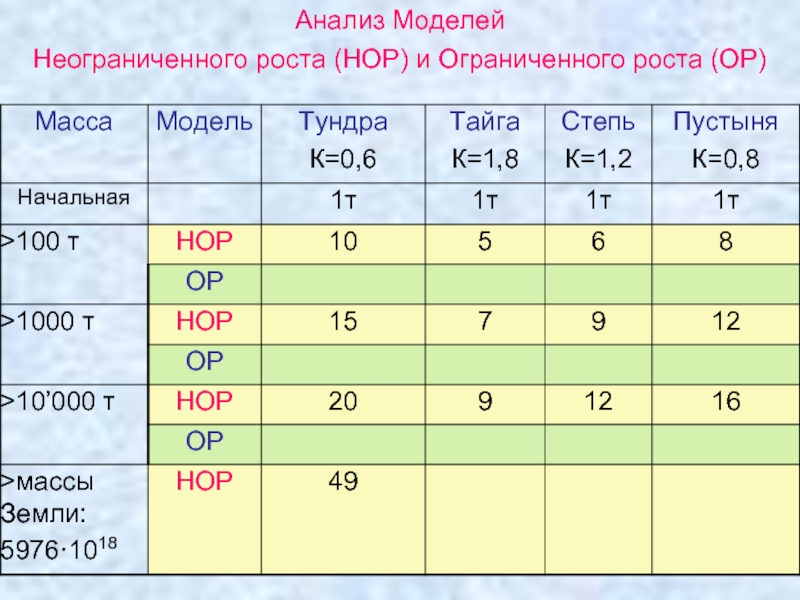
Слайд 21Выводы:
I.Модель неограниченного роста (НОР)
На увеличение массы в 10 раз потребовалось 2-3
Модель НОР не годится для решения задачи популяции, хотя и адекватна до некоторого момента.
Сл-но, для выяснения непригодности какой-либо модели она должна быть построена
Выводы:
Слайд 22Л/работа «Модель ограниченного роста (ОР)»
Построение модели
Существенные факторы:
Прирост массы живых организмов за
Существует некоторое предельное значение массы живых организмов
Коэффициент прироста массы живых организмов k за ед. времени пропорционален разности между максимально возможным значением массы и массой, имеющейся к данному моменту времени
2. Параметры модели.
Дано:
М(0) – начальная масса живых организмов
L – предельное значение массы живых организмов
a – коэффициент пропорциональности в формуле для коэффициента прироста
n – время
Найти: M(n) – массу живых организмов через n лет
3. Связь: a=k/ (L - M(0)) для n=0,1,2,3… M(n+1) =M(n) + a·M(n)·(L - M(n))
Слайд 24Выводы:
I.Модель ограниченного роста (ОР)
На начальных этапах развития популяции значение массы живых
Чем медленнее рост (меньше К), тем больше требуется время на удесятерение массы растений
Строящаяся модель зависит от того, какими будут параметры, описывающие существенные факторы
Для описания одного и того же фактора может быть взята разная система параметров, ⇒ это приводит к появлению разных моделей
Слайд 25Адекватность модели
Если модель дает удовлетворительные результаты при решении задач, то говорят,
Никакая модель не эквивалентна исходному объекту, процессу или явлению
Адекватность модели определяется ее согласованностью с практикой и общетеоретическими положениями
Область адекватности модели – совокупность всех тех ситуаций, в которых применяется данная модель
Всякая модель имеет ограниченную область адекватности, и за ее пределами она перестает удовлетворительно отражать свойства моделируемого объекта. Поэтому и применять модель для решения той или иной жизненной задачи допустимо только тогда, когда мы убедились, что не вышли за границы области адекватности.
Слайд 26Что значит найти границы адекватности данной модели?
- необходимо установить, в
Как находить границы адекватности модели?
Проведение натурного эксперимента
Проведение компьютерного эксперимента, опирающегося на общетеоретические положения
Слайд 27Неадекватность модели может проявляться:
В несоответствии результатов, полученных с помощью этой модели,
В противоречии результатов, полученных с помощью этой модели, с теорией, справедливость которой доказана
Неадекватность модели всегда является следствием того, что при ее построении не были учтены какие-то существенные факторы
Факторы, определяющие смену модели:
Возникновение противоречий с практикой в виде реальной деятельности человека
Возникновение противоречий с более общей теорией
Появление более совершенного языка описания моделей
Появление более мощных средств реализации моделей
Слайд 28Л/работа «Поиск границ адекватности модели»
Цель: исследовать модель Неограниченного роста на адекватность
Критерии
Оценка адекватности погрешностью отклонения массы, рассчитанной по НОР, от массы, рассчитанной по модели ОР. Критерий отклонения: М(n) – Mo(n) ≤ 10%
Найти функцию f(k,L), такую, что при n < f(k,L) модель НОР удовлетворяет сформулированному критерию адекватности
Попытаемся определить, насколько мала должна быть исходная масса живых организмов по отношению к предельной массе, чтобы модель неограниченного роста оставалась адекватной в течение нескольких лет
Слайд 29
Модель
неограниченного роста
Параметры модели
Дано:
М(0) – начальная масса живых организмов
К –
n – время
Найти: M(n) – массу живых организмов через n лет
Связь:
M(n+1) = (1 +k)·M(n)
Модель ограниченного роста
Параметры модели.
Дано:
Мо(0) – начальная масса живых организмов
К – коэффициет прироста
L – предельное значение массы живых организмов
a – коэффициент пропорциональности в формуле для коэффициента прироста
n – время
Найти: Mо(n) – массу живых организмов через n лет
Связь:
Mо(n) – вычисление массы в модели ограниченного роста. Т.к Mо(0) = М(0) то, Mо(1)=М(1). Но Mо(2)<М(2) и далее различие будет больше между Mо и M. ⇒ необходимо договориться какое расхождение между ними будем считать допустимым. Например, модель неограниченного роста считаем адекватной, если
М – Мо ≤10%
Слайд 30Зависимость границы адекватности n от k и L
При уменьшении K граница
При увеличении L в 2 раза граница n отодвигается на 1 год, ⇒ L образует геометрическую прогрессию относительно границы адекватности n,
⇒ L= b·2n-1, где b – коэфф-т, b=L/2n-1 Но K(n)= a(L-M(n)) для n=0,1,2,3… ⇒ L-M(n)=K(n)/a ⇒ L=K(n)/a+M(n), т.е. участвует еще и К.
При К=1 выполняется соотношение 2=1+К ⇒ можно предположить, что L=b(1+K)n-1 ⇒ b=L/(1+K)n-1 Нетрудно проверить, что b не зависит от К и при различных К значение b≈8
⇒ Вывод: моделью НОР можно пользоваться с учетом погрешности в 10% при выполнении условия L ≥ 8(1+k)n-1
8
10
12
13
14
11
Слайд 31Решая показательное неравенство L ≥ 8(1+k)n-1 , получим выражение для n,
⇒ существует функция f(k,L), определяющая границу адекватности модели
Итак, с помощью ИТ:
Исследован характер зависимости между различными переменными
Выдвигаются и проверяются в компьютерном эксперименте гипотезы о формуле для этой зависимости
Слайд 34Модель потребления возобновляемых ресурсов
Целенаправленное воздействие на факторы динамической системы называется управлением
Виды природных ресурсов:
Возобновляемые (леса)
Невозобновляемые (руда)
Задача управления: Сколько леса можно рубить ежегодно, чтобы обеспечить его нормальное воспроизводство?
Модель ограниченного роста – модель прироста растительной массы без вмешательства человека
Модель потребления возобновляемых ресурсов
Слайд 35Л/работа «Управление добычей возобновляемых ресурсов»
Построение модели
Существенные факторы:
Прирост массы живых организмов за
Существует некоторое предельное значение массы живых организмов
Коэффициент прироста массы живых организмов k за ед. времени пропорционален разности между максимально возможным значением массы и массой, имеющейся к данному моменту времени
Величина ежегодно изымаемого ресурса постоянна
2. Параметры модели. Дано:
М(0) – начальная масса живых организмов
L – предельное значение массы живых организмов
a – коэффициент пропорциональности в формуле для коэффициента прироста
n – время
R – величина ежегодного потребления возобновляемого ресурса
Найти: M(n) – количество ресурса через n лет
3. Связь: