Кибернетики
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Коллизии хеш-функций презентация
Содержание
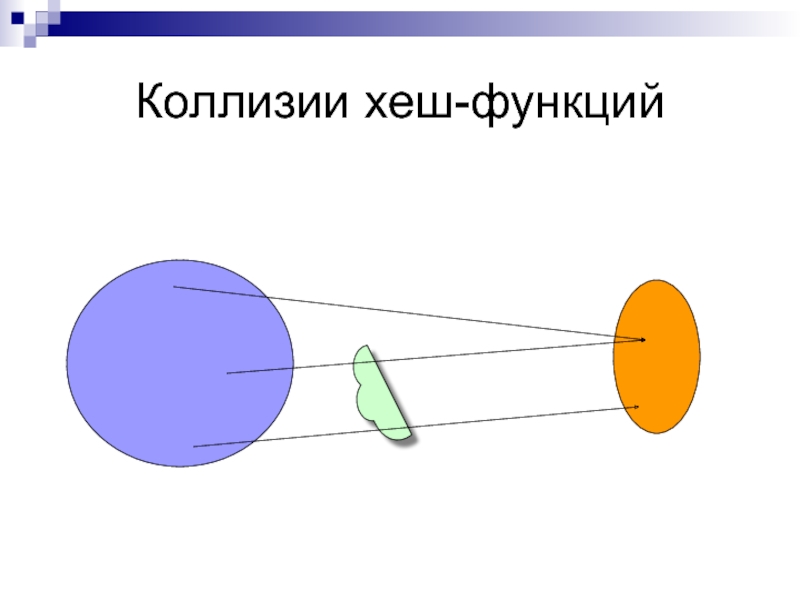
- 1. Коллизии хеш-функций
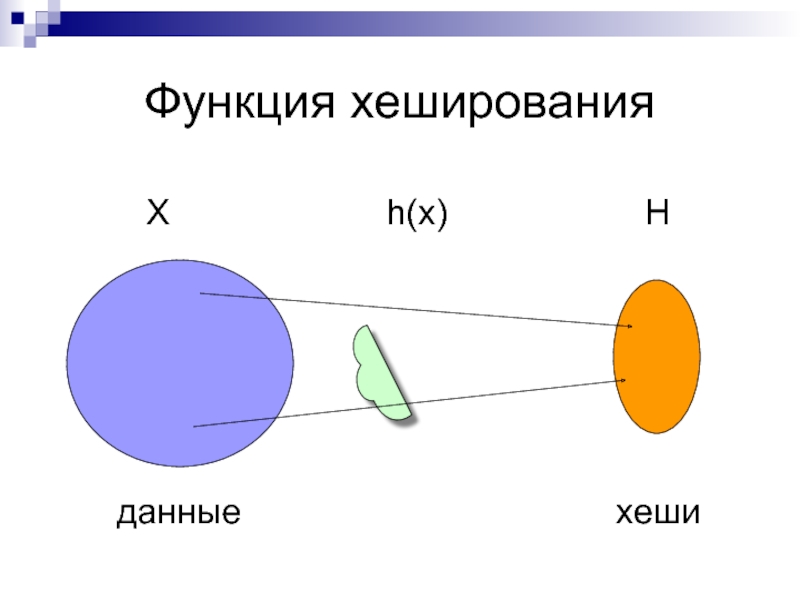
- 2. Функция хеширования
- 3. Функция хеширования Свойства: Необратимость
- 5. Коллизии хеш-функций Практически любая хеш-функция имеет коллизии
- 6. Коллизии хеш-функций
- 7. Типы атак на хеш-функции
- 8. MD5 Доббертин (1996г) Псевдоколлизия – использовал свои
- 9. SHA-0 Ванг Атака методом дифференциальных путей
- 10. SHA-1 Ванг, Йинг, Ю Расширимые сообщения –
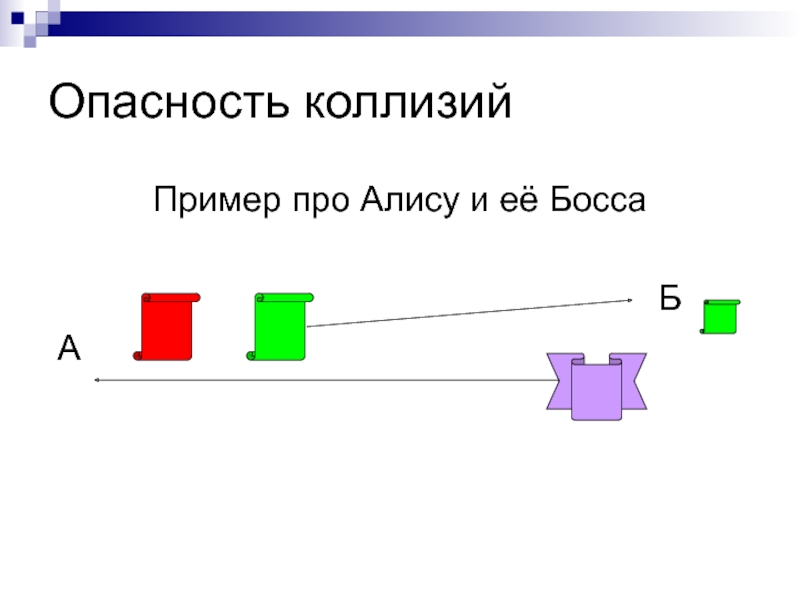
- 11. Опасность коллизий Пример про Алису и её
- 12. Опасность коллизий Пример про Алису и
- 13. Спасибо за внимание
Слайд 1Коллизии
хеш-функций
MD5, SHA-0, SHA-1
Московский физико-технический институт (ГУ МФТИ)
Факультет Радиотехники и
Слайд 3Функция хеширования
Свойства:
Необратимость
Стойкость к коллизиям
Слабая
Сильная
Применение в криптографии
ЭЦП, пароли и т.д.
Слайд 4
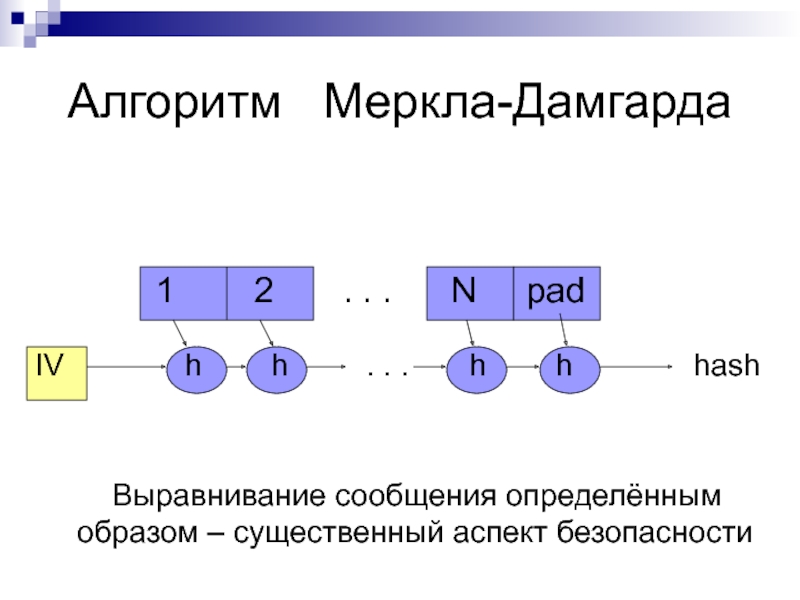
Алгоритм Меркла-Дамгарда
1
2 . . . N pad
IV h h . . . h h hash
Выравнивание сообщения определённым образом – существенный аспект безопасности
IV h h . . . h h hash
Выравнивание сообщения определённым образом – существенный аспект безопасности
Слайд 5Коллизии хеш-функций
Практически любая хеш-функция имеет коллизии
В хороших х.ф. коллизии крайне редки
«Идеальная
х.ф.» - если заранее известны все значения входных данных
Слайд 7Типы атак на хеш-функции
Для n-битной
хеш-функции
Атака на обнаружение коллизий
Требует ~ 2n/2 операций (парадокс дней рождения)
Атака на нахождение прообраза
Требует ~ 2n операций
Атака на обнаружение коллизий
Требует ~ 2n/2 операций (парадокс дней рождения)
Атака на нахождение прообраза
Требует ~ 2n операций
Слайд 8MD5
Доббертин (1996г)
Псевдоколлизия – использовал свои IV
Если MD5(x) = MD5(y), то MD5(x||S)
= MD5(y||S)
Ванг и Ю
Мощный метод нахождения коллизий, основанный на дифференциальной атаке. ~ 240 операций
Были приведены некоторые коллизии и написана программа для генерирования архивов и документов PDF с одинаковыми хешами
Ванг и Ю
Мощный метод нахождения коллизий, основанный на дифференциальной атаке. ~ 240 операций
Были приведены некоторые коллизии и написана программа для генерирования архивов и документов PDF с одинаковыми хешами
Слайд 9SHA-0
Ванг
Атака методом дифференциальных путей
Используется возможность создания локальных коллизий в
SHA-0
Сложность «прямой» реализации ~ 242 операций
Можно заранее составить таблицу подходящих сообщений, тогда сложность составляет ~ 239 операций
Сложность «прямой» реализации ~ 242 операций
Можно заранее составить таблицу подходящих сообщений, тогда сложность составляет ~ 239 операций
Слайд 10SHA-1
Ванг, Йинг, Ю
Расширимые сообщения – разновидность множественной коллизии.
Атака с использованием очень
длинных сообщений
Находят все промежуточные хеши для очень длинного сообщения и перебирают около 2106 блоков до совпадения с одним из исходных. Находят расширимое сообщение и расширяют его до длины исходного. Получают второй прообраз.
Находят все промежуточные хеши для очень длинного сообщения и перебирают около 2106 блоков до совпадения с одним из исходных. Находят расширимое сообщение и расширяют его до длины исходного. Получают второй прообраз.