- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Категорические высказывания презентация
Содержание
- 1. Категорические высказывания
- 2. Простое высказывание состоит из субъекта, предиката и связки. Альберт Великий искал философский камень
- 3. Субъект и предикат – термины, а
- 4. Платон – грек S – Платон, единичный
- 5. Предикат обозначает свойства предметов. Поскольку главным
- 6. Но существуют категорические высказывания, которые образуются
- 7. Классификация высказываний по количеству и качеству
- 8. В зависимости от того, обо всем ли
- 9. Объединенная классификация высказываний по количеству и
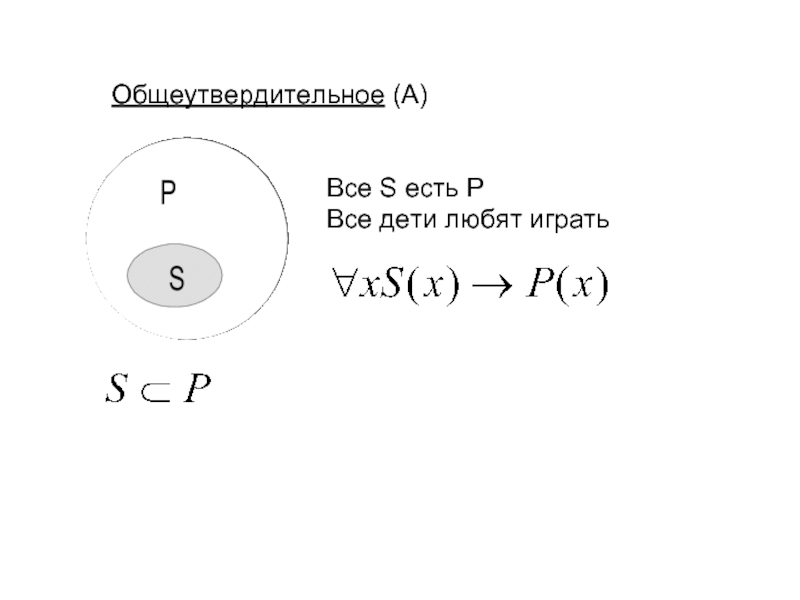
- 10. Общеутвердительное (А) Все S есть Р Все дети любят играть
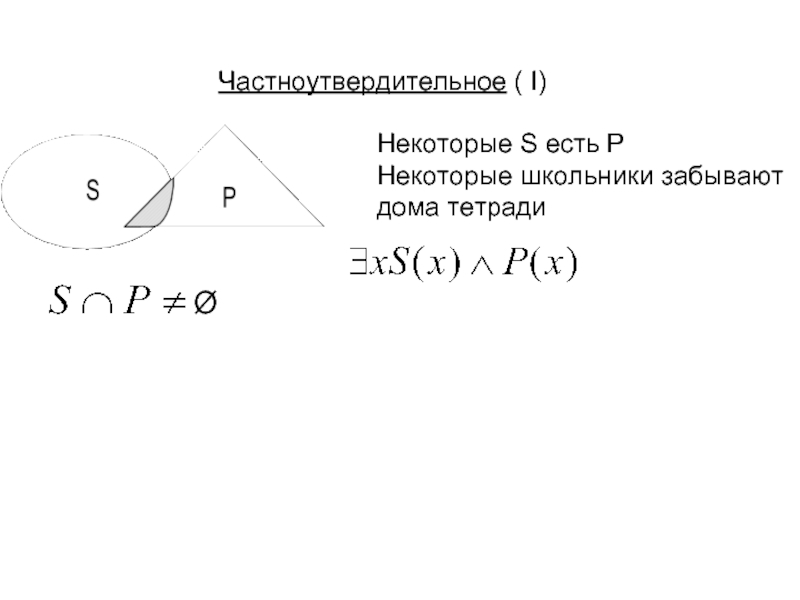
- 11. Частноутвердительное ( I) Некоторые S
- 12. . Ø Общеотрицательные (E) Ни
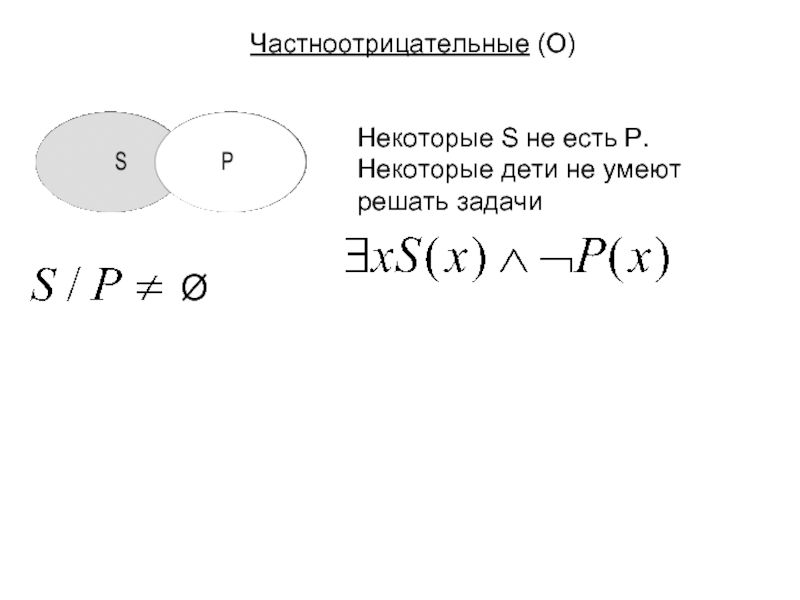
- 13. . Ø Частноотрицательные (О) Некоторые
- 14. Буквы А и I взяты из латинского
- 15. СР-1
Слайд 2Простое высказывание состоит из субъекта, предиката и связки.
Альберт Великий искал философский
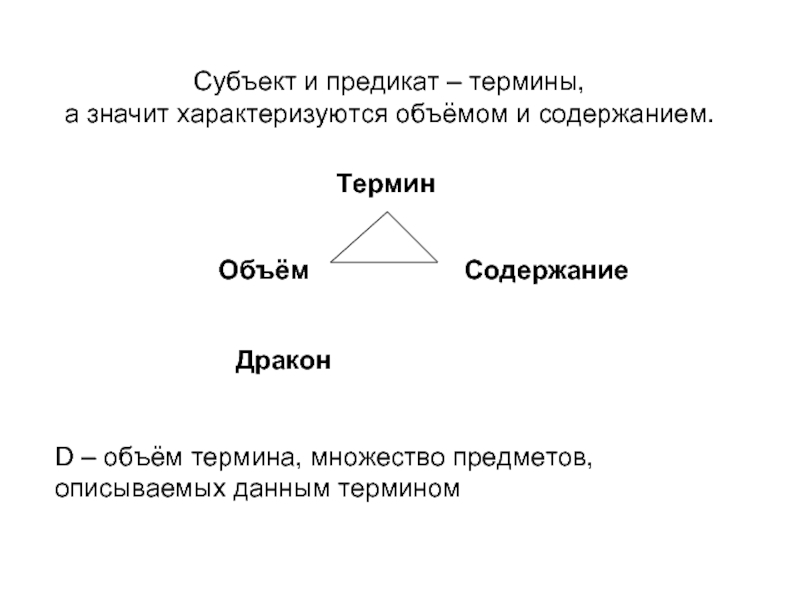
Слайд 3Субъект и предикат – термины,
а значит характеризуются объёмом и содержанием.
Термин
Объём
Содержание
Дракон
D – объём термина, множество предметов,
описываемых данным термином
Слайд 4Платон – грек
S – Платон, единичный термин
Обобщением его является
х есть
Для некоторых х оно истинно: Гр(х)=Аристотель
Слайд 5Предикат обозначает свойства предметов.
Поскольку главным здесь являются свойства,
то такая
Выражения вида «х есть грек» называют предикатами.
Предикат – это выражение с переменной,
оно иногда истинно, а иногда ложно
Слайд 6Но существуют категорические высказывания,
которые образуются из предикатов добавлением
слов «все,
Эти слова называются кванторами.
Слайд 7Классификация высказываний
по количеству и качеству
Категорические высказывания делятся по качеству связки
(«есть» или «не есть»)
на утвердительные или отрицательные.
«Ни один попугай не живёт в Сибири» – отрицательное,
«Все львы едят мясо» – положительное
Слайд 8В зависимости от того, обо всем ли объеме субъекта
идет речь
высказывания подразделяются на общие и частные.
Это деление высказываний по количеству.
Для общих высказываний кванторы : все, каждый,
ни один и другие.
Для частных высказываний – многие, некоторые , …
Иногда квантор только подразумевается.
Если субъектом является единичный термин,
то высказывание относят к общим
Слайд 9Объединенная классификация высказываний
по количеству и качеству
Объединенная классификация высказываний
по количеству
4-х типов:
Слайд 14Буквы А и I взяты из латинского слова affirmo ( утверждаю,),
а Е и О – из латинского слова nego (отрицаю).
.
Установите количество и качество следующих суждений и
дайте им стандартную форму одного из четырех типов
А, Е, I, О, запишите его в символическом виде и укажите
отношение между объёмами S и Р.
а) рыбы дышат жабрами.
б)Некоторые выдающиеся математики не приняли
неевклидовой геометрии.