Как вы думаете, в каком классе учится Алена, и что нового она узнала в школе?
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Как вы думаете, в каком классе учится Алена, и что нового она узнала в школе? презентация
Содержание
- 1. Как вы думаете, в каком классе учится Алена, и что нового она узнала в школе?
- 3. Закончился 20 -ый век. Куда стремится человек?
- 4. Слово прогрессия имеет латинское происхождение и означает “движение вперед”. Любая работа в
- 5. Цели урока: Отрабатывать навыки работы с формулами
- 6. Ход урока Организационный момент. Устная работа
- 7. Устная работа Определите, какая последовательность является
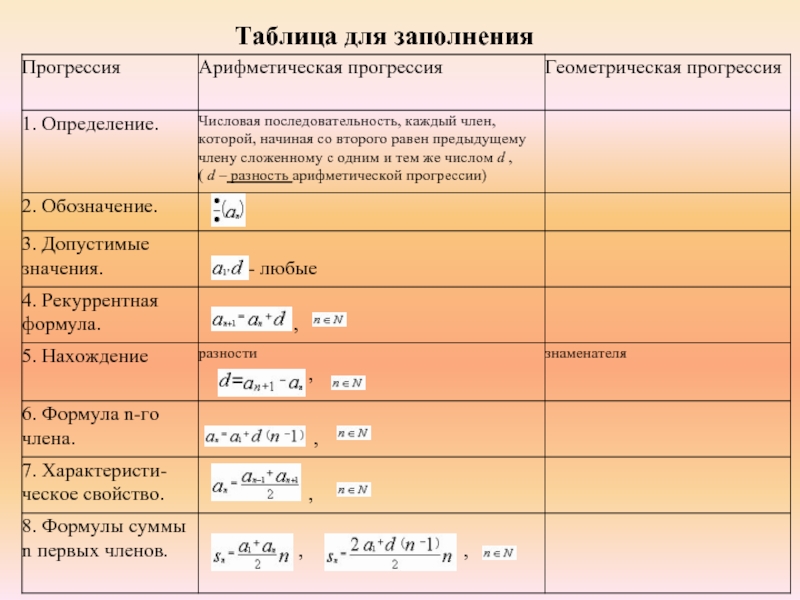
- 8. Таблица для заполнения
- 9. Герберт Спенсер, английский философ, когда-то сказал: "Дороги
- 10. Формулы
- 11. Код ответа 813 426 795
- 12. Древняя индийская легенда Сколько зёрен должен
- 13. 18 446 744 073 704 551 615
- 14. Современники сказали бы так:
- 15. Если бы царю удалось засеять
- 16. Если считать, что 1 пуд зерна
- 17. Немного истории Понятие числовой последовательности возникло и
- 18. В XVIII в. в английских учебниках
- 19. Древняя Греция Сведения, связанные
- 20. Древний Египет Задача из египетского папируса Ахмеса:
- 21. Германия Нашел моментально сумму всех натуральных чисел
- 22. «Умение решать задачи – практическое искусство, подобное
- 23. Все организмы обладают интенсивностью размножения в
- 24. Задача Бактерия, попав в живой организм, к
- 25. Решение. S72=272-1= 4 722
- 26. Способность к размножению у бактерий настолько
- 27. ТЕСТ и Г И А
- 28. Задачи на прогрессии есть и в книгах Я.И. Перельмана
- 29. "Прогрессия - движение вперёд!" Урок сегодня
- 30. Домашнее задание: 1)
Слайд 1Алена довольная пришла из школы и предложила папе заключить сделку: в
Слайд 3Закончился 20 -ый век. Куда стремится человек? Изучен космос и моря,
"Прогрессия - движение вперёд!"
Слайд 4Слово прогрессия имеет латинское происхождение и означает “движение вперед”. Любая работа в математике начинается с правил,
Слайд 5Цели урока:
Отрабатывать навыки работы с формулами геометрической прогрессии;
Показать практическую значимость формулы
Убедиться в том, что алгебра является частью общечеловеческой культуры.
Слайд 6Ход урока
Организационный момент.
Устная работа
Проверка теоретического материала
Работа с формулами
Задача-легенда
Историческая
Задача на применение темы
Задания ГИА
Интерактивный тест
Итог урока
Слайд 7Устная работа
Определите, какая последовательность является геометрической прогрессией
2; 5;
2; 1; 0,5; 0,25
-2; -8; -32; -128 …
-2; -4; -6; -8; …
3) 21 ; 22 ; 23 ; 24 ; …; 210
2) Найдите знаменатель
геометрической прогрессии
b2 = 4; b3 = 16
b3 = 16; b4 = 4
b8 = 9; b9 = -27
b9 = -27; b10 = 9
4) ½ - 1; ⅓ - 1 ; ⅔ - 1.
Слайд 9Герберт Спенсер, английский философ, когда-то сказал: "Дороги не те знания, которые
Слайд 12Древняя индийская легенда
Сколько зёрен должен был получить изобретатель шахмат?
S 64 = 2 - 1=
=18 446 744 073 704 551 615
64
Слайд 1318 446 744 073 704 551 615 18 квинтиллионов 446 квадриллионов 744 триллиона 73 миллиарда(биллиона) 709
Слайд 15 Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая
Слайд 16 Если считать, что 1 пуд зерна содержит 40000 зерен, то для
Слайд 17Немного истории
Понятие числовой последовательности возникло и развивалось задолго до создания учения
На связь между прогрессиями первым обратил внимание великий АРХИМЕД (ок. 287–212 гг. до н.э)
Термин “прогрессия” был введен римским автором Боэцием (в 6 веке) и понимался в более широком смысле, как бесконечная числовая последовательность. Названия “арифметическая” и “геометрическая” были перенесены из теории непрерывных пропорций, которыми занимались древние греки.
Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (в 3 веке). Формула суммы
членов геометрической прогрессии дана в книге Евклида “Начала”
(3 век до н.э.).
Правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении «Книги абака» в 1202г. (Леонардо Пизанский)
Слайд 18
В XVIII в. в английских учебниках появились обозначения арифметической и геометрической
Арифметическая
Геометрическая
А общее правило для суммирования любой конечной геометрической прогрессии встречается в книге Н. Шюке «Наука о числах», увидевшей свет в 1484 году.
Наука о числах
Англия XVIII век
Слайд 19Древняя Греция
Сведения, связанные с прогрессиями, впервые встречаются в дошедших
Слайд 20Древний Египет
Задача из египетского папируса Ахмеса: «Пусть тебе сказано: раздели 10
Формула, которой пользовались египтяне:
Слайд 21Германия
Нашел моментально сумму всех натуральных чисел от 1 до 40, будучи
1 + 2 + 3 + 4 + ….. + 39 + 40 = (1 + 40) + (2 + 39) + …… + (20 + 21) = 41 ∙ 20 = 820
КАРЛ ГАУСС
(1777 – 1855)
Слайд 22«Умение решать задачи – практическое искусство, подобное плаванию или катанию на
Слайд 23Все организмы обладают интенсивностью
размножения в геометрической прогрессии
Известно, что бактерии
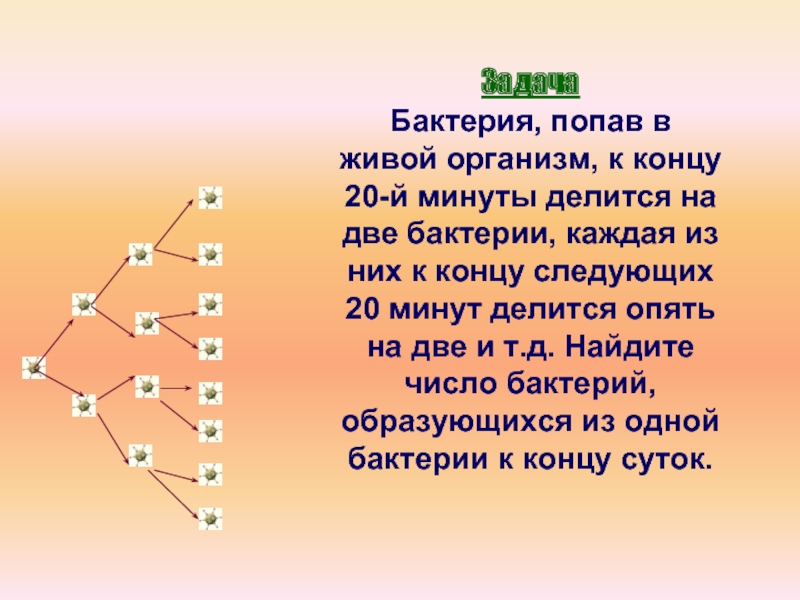
Слайд 24Задача
Бактерия, попав в живой организм, к концу 20-й минуты делится на
Слайд 25Решение. S72=272-1= 4 722 366 482 869 645 709
Всего бактерий
4 септиллиона
722 сектиллиона
366 квинтиллионов
482 квадриллиона
869 триллионов
645 миллиардов
709 миллионов
213 тысяч 695
Слайд 26 Способность к размножению у бактерий настолько велика, что если бы
Слайд 29"Прогрессия - движение вперёд!"
Урок сегодня завершён,
Но каждый должен знать:
Познание, упорство,
Слайд 30Домашнее задание:
1) Алена должна получить
234-1=
171 798 691,83руб
2)
Удивительно, как быстро разлетаются по деревне слухи! Иной раз не пройдет и двух часов со времени какого– нибудь происшествия, которое видели всего несколько человек, а новость уже облетела всё село: все о ней знают, все слышали.
Итак, задача:
В селе 1 000 жителей. Приезжий в 8.00 рассказывает новость трем соседям; каждый из них рассказывает новость уже трем своим соседям и т. д. Во сколько эта новость станет известна всему селу?