- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
к о н у с презентация
Содержание
- 1. к о н у с
- 2. Содержание определение конуса построение сечений виды площадь
- 3. Конусом называется тело, которое состоит
- 4. Кругом называется фигура, которая состоит из всех
- 5. в s ОБРАЗУЮЩИЕ -
- 6. Сечения конуса
- 7. сечения конуса сечение конуса плоскостью,
- 8. Сечения конуса сечение конуса плоскостью параллельной основанию круг
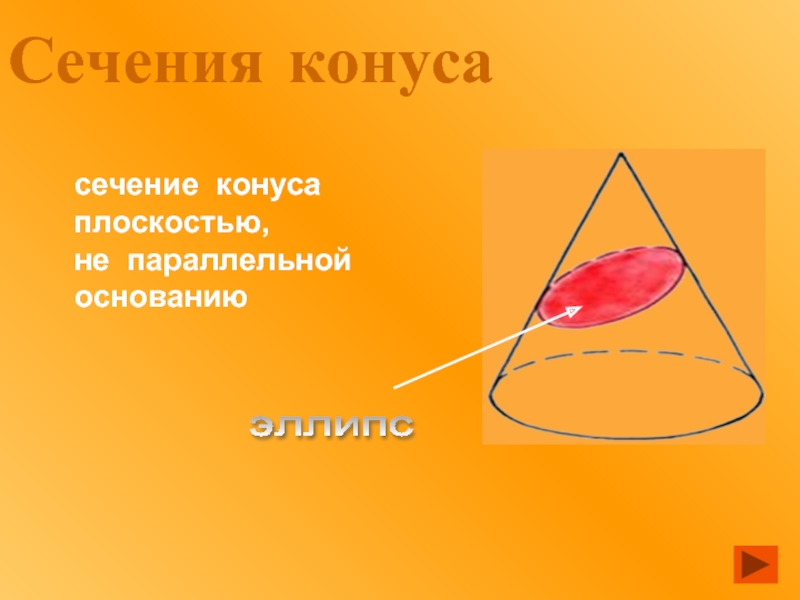
- 9. Сечения конуса эллипс сечение конуса плоскостью, не параллельной основанию
- 10. Сечения конуса о о S А
- 11. Прямой конус Конус называется прямым,
- 12. Площадь поверхности объем
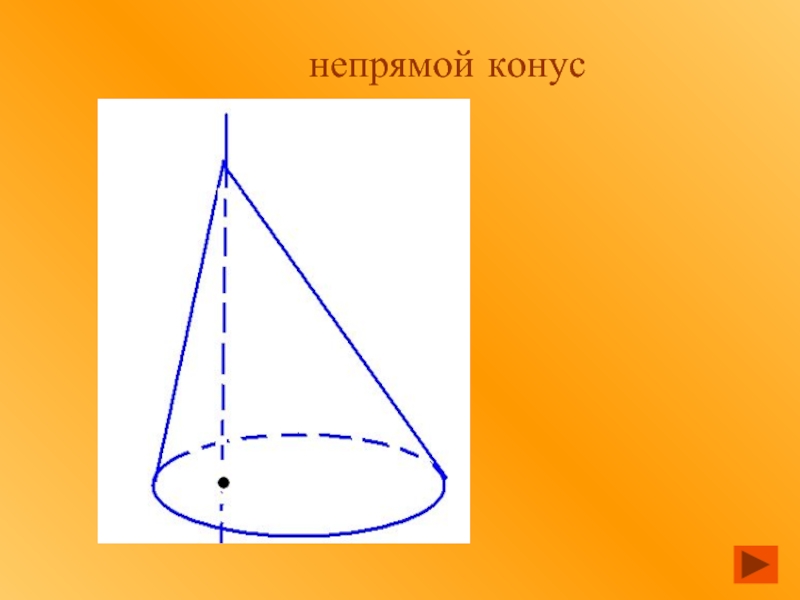
- 13. непрямой конус
- 14. Усеченный конус Тело, полученное при
- 15. Площадь поверхности объем
- 16. пирамида, вписанная в конус Пирамидой,
- 17. пирамида,описанная около конуса Пирамидой, описанной около
- 18. У пирамиды все боковые ребра равны. Докажите,
- 19. Т Е С Т 1. Выберите неверное
- 20. 2. Длина образующей конуса – 10
- 21. 3. Объём конуса равен 18π дм3. Осевое
- 22. молодец! Перейти к домашнему заданию
- 23. Подумай еще
- 24. неверно
- 25. домашнее задание Найти объем цилиндра, вписанного
Слайд 2Содержание
определение конуса
построение сечений
виды
площадь поверхности, объем
вписанная и описанная пирамида
решение задач
Слайд 3Конусом называется тело, которое состоит
из круга - основания конуса,
точки,
всех отрезков, соединяющих вершину конуса с
точками основания
Слайд 4Кругом называется фигура, которая состоит из всех точек плоскости, расстояние от
Слайд 5
в
s
ОБРАЗУЮЩИЕ -
А
с
д
о
SA, SC,SD,SB…
SO
ОТРЕЗКИ, СОЕДИНЯЮЩИЕ ВЕРШИНУ КОНУСА С ТОЧКАМИ ОКРУЖНОСТИ
перпендикуляр,
ось-
ПРЯМАЯ, СОДЕРЖАЩАЯ ЕГО ВЫСОТУ
высота -
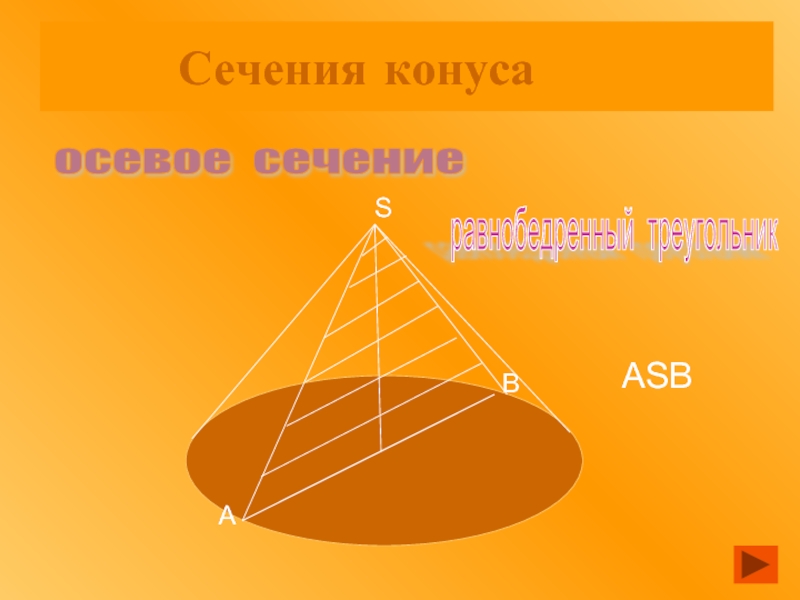
Слайд 7сечения конуса
сечение конуса плоскостью, проходящей через ось конуса, называется осевым
осевое сечение
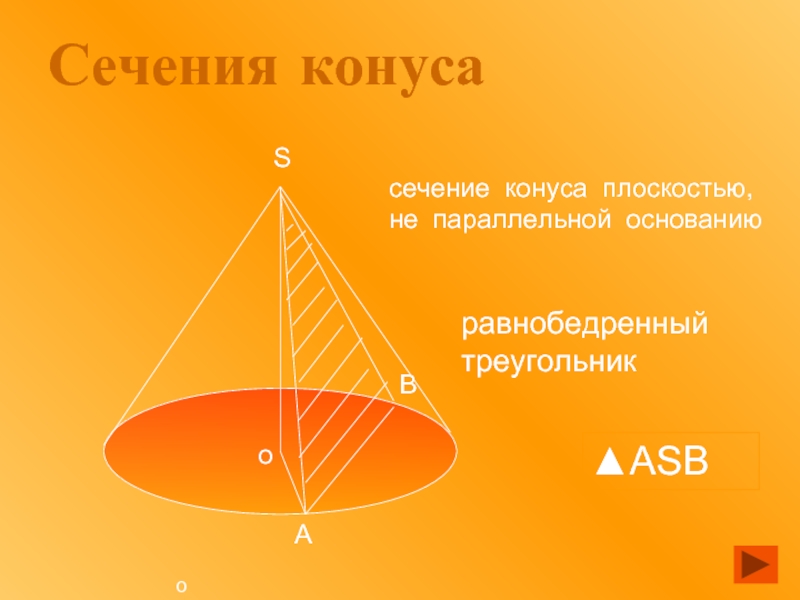
Слайд 10Сечения конуса
о
о
S
А
В
▲АSВ
равнобедренный треугольник
сечение конуса плоскостью,
не параллельной основанию
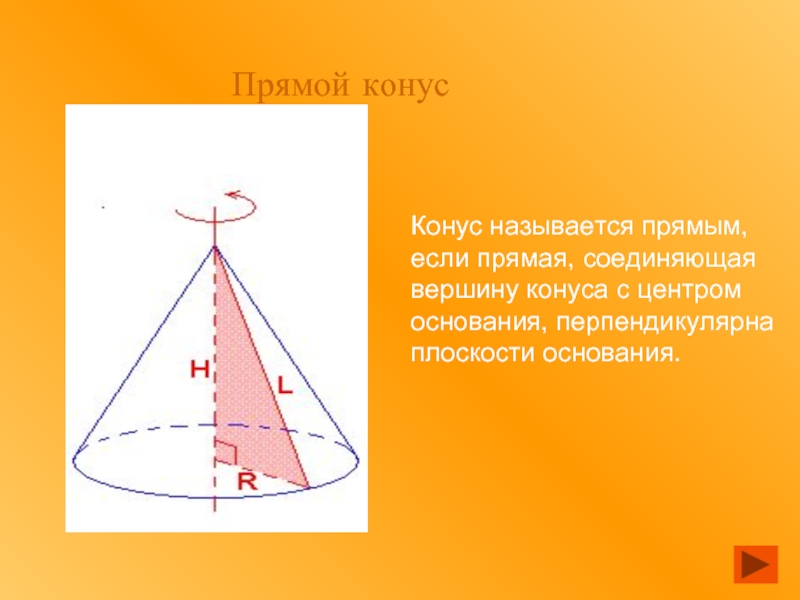
Слайд 11Прямой конус
Конус называется прямым, если прямая, соединяющая вершину конуса с
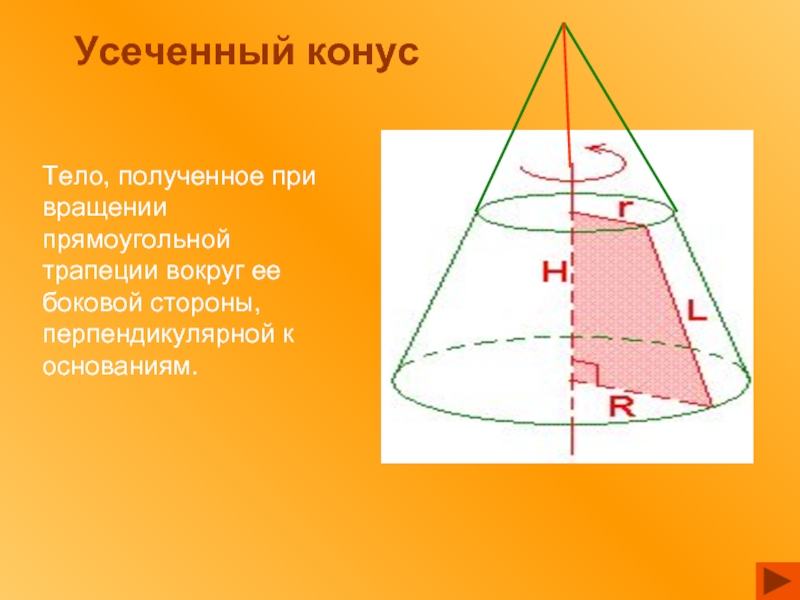
Слайд 14Усеченный конус
Тело, полученное при вращении прямоугольной трапеции вокруг ее боковой
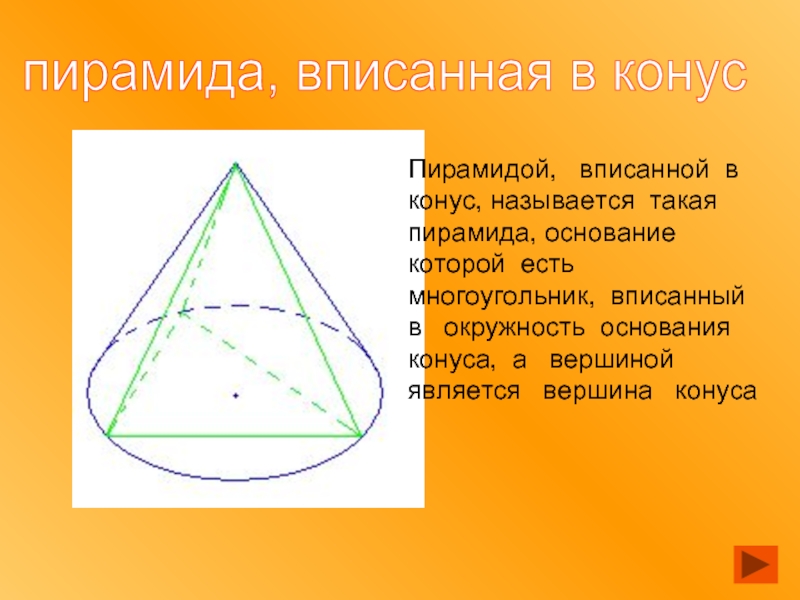
Слайд 16пирамида, вписанная в конус
Пирамидой, вписанной в конус, называется такая
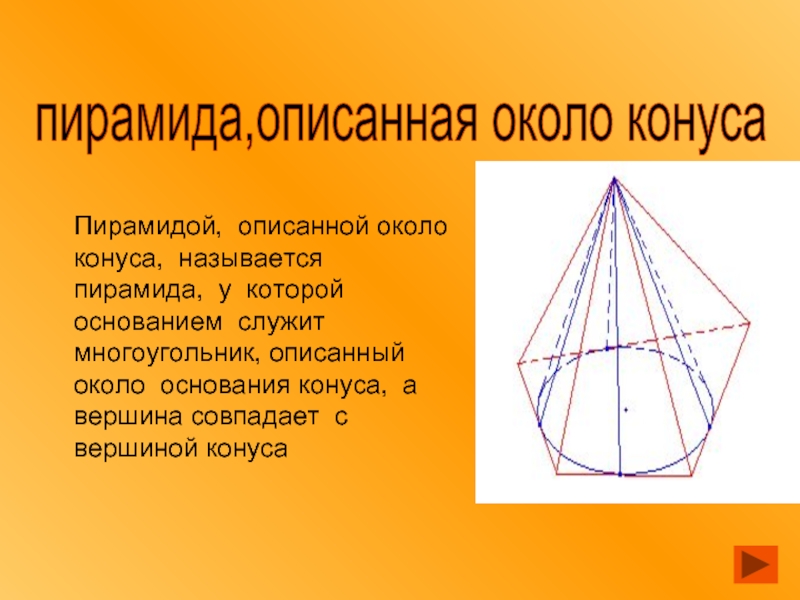
Слайд 17пирамида,описанная около конуса
Пирамидой, описанной около
конуса, называется пирамида, у которой
многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса
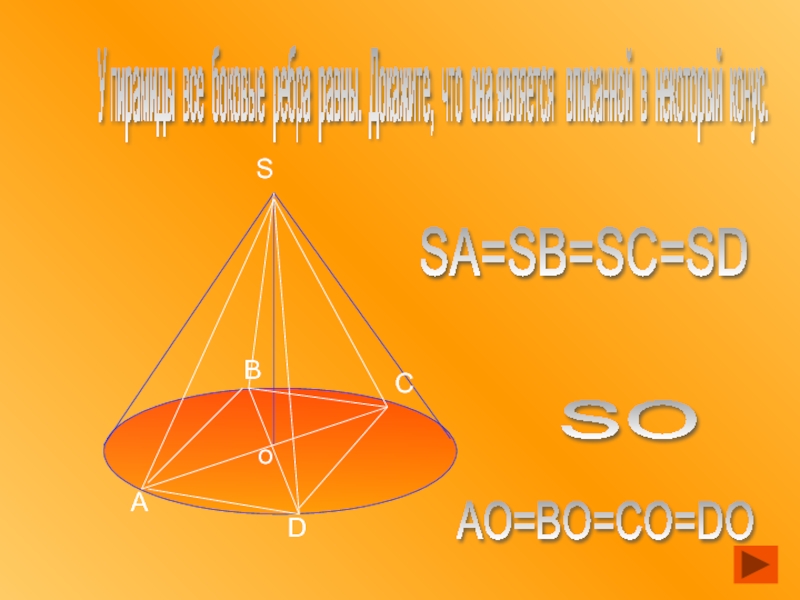
Слайд 18У пирамиды все боковые ребра равны. Докажите, что она является
о
А
В
S
C
D
SA=SB=SC=SD
AO=BO=CO=DO
SO
Слайд 19Т Е С Т
1. Выберите неверное утверждение:
аа). а). Конус может быть
бб). Прямая, проходящая через вершину конуса и центр его основания, называется осью конуса.
в). Площадь боковой поверхности конуса может быть вычислена по формуле Sб = Пr(r+l)
г). г). Осевым сечением усеченного конуса является равнобедренная трапеция
д). д). Конус называется равносторонним, если его осевое сечение правильный треугольник
Слайд 20
2. Длина образующей конуса – 10 см,
диаметр его основания -
Найти высоту конуса.
Т Е С Т
Слайд 213. Объём конуса равен 18π дм3. Осевое сечение конуса – прямоугольный
Т Е С Т