- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ИНФОРМАЦИЯ презентация
Содержание
- 1. ИНФОРМАЦИЯ
- 2. Неопределённость знаний и единица информации.
- 3. Что такое «неопределённость знаний»?
- 4. Задача 1: студент на экзамене может получить
- 5. Метод поиска, на каждом шаге которого
- 6. Получим формулу, по которой вычисляется количество
- 8. КОЛИЧЕСТВО
- 9. ИНФОРМАЦИЯ Тема 4.
- 10. Алфавитный подход является объективным способом измерения
- 11. Правило, как измерить информацию,
- 12. Например:
- 13. Примеры: Для передачи секретного сообщения используется код,
Слайд 2
Неопределённость знаний и единица информации.
Пока мы рассматривали лишь две ситуации: «нет
Единица измерения информации была определена в науке, которая называется теорией информации. Эта единица называется «бит». Её определение звучит так:
Сообщение, уменьшающее неопределённость знаний в два раза, несёт 1 бит информации.
Слайд 3Что такое «неопределённость знаний»?
Допустим, вы бросаете монету, загадывая,
В этом случае перед подбрасыванием монеты неопределённость знаний о результате равна двум.
Игральный кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределённость знаний о результате бросания кубика равна шести.
Следовательно, можно сказать так: неопределённость знаний о некотором событии — это количество возможных результатов события (бросания монеты, кубика; вытаскивания жребия).
Пример с монетой. После того, как вы бросили монету и посмотрели на неё, вы получили зрительное сообщение, что выпал, например, орёл. Произошла одно из двух возможных событий. Неопределённость знаний уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили 1 бит информации
Сообщение о том, что произошло одно событие из двух равновероятных, несёт 1 бит информации.
Слайд 4Задача 1: студент на экзамене может получить одну из четырёх оценок:
Вопрос. Сколько бит информации содержится в его ответе?
Подойдём к ответу постепенно. Будем отгадывать оценку, задавая вопросы, на которые можно ответить только «да» или «нет». Вопросы будем ставить так, чтобы каждый ответ уменьшал количество вариантов в два раза и, следовательно, приносил 1 бит информации. Первый вопрос: Оценка выше тройки? - Да!
После этого ответа число вариантов уменьшилось в два раза. Остались только «4» и «5». Получен 1 бит информации Второй вопрос: Ты получил пятёрку? - Нет! Выбран один вариант из двух оставшихся: оценка – «четвёрка». Получен еще 1 бит информации. В сумме имеем 2 бита. Сообщение о том, что произошло одно из четырёх равновероятных событий, несёт 2 бита информации.
Слайд 5
Метод поиска, на каждом шаге которого отбрасывается половина вариантов, называется
методом
Задача 2: На книжном стеллаже восемь полок. Книга может быть поставлена на любую из них. Сколько информации содержит сообщение о том, где находится книга Задаём вопросы: Книга лежит выше четвёртой полки? - Нет.
Книга лежит ниже третьей полки? - Да.
Книга – на второй полке? - Нет.
Ну теперь всё ясно! Книга лежит на первой полке!
Каждый ответ уменьшал неопределённость в два раза. Всего было задано три вопроса. Значит, набрано 3 бита информации. И если бы сразу было сказано, что книга лежит на первой полке, то этим сообщением были бы переданы те же 3 бита информации.
Слайд 6 Получим формулу, по которой вычисляется количество
Обозначим буквой K количество возможных событий, или, это - неопределённость знаний.
Буквой i обозначим количество информации в сообщении о том, что произошло одно из N событий.
В примере с монетой K = 2, i = 1.
В примере с оценками K = 4, i = 2.
В примере со стеллажом K = 8, i = 3.
Связь между этими величинами выражается формулой: 2i = K
Слайд 7
Если значение K равно целой степени
А чему равно количество информации в сообщении о результате бросания игральной кости, у которой имеется шесть граней и, следовательно, K = 6?
Решение уравнения 2i = 6
будет дробным числом, лежащим между числами 2 и 3, поскольку 22 = 4, а 23 = 8. С точностью до пяти знаков после запятой решение такое: 2,58496.
Количество информации i, содержащееся в
сообщении о том, что произошло одно из K
равновероятных событий, определяется из
решения показательного уравнения:
2i = K.
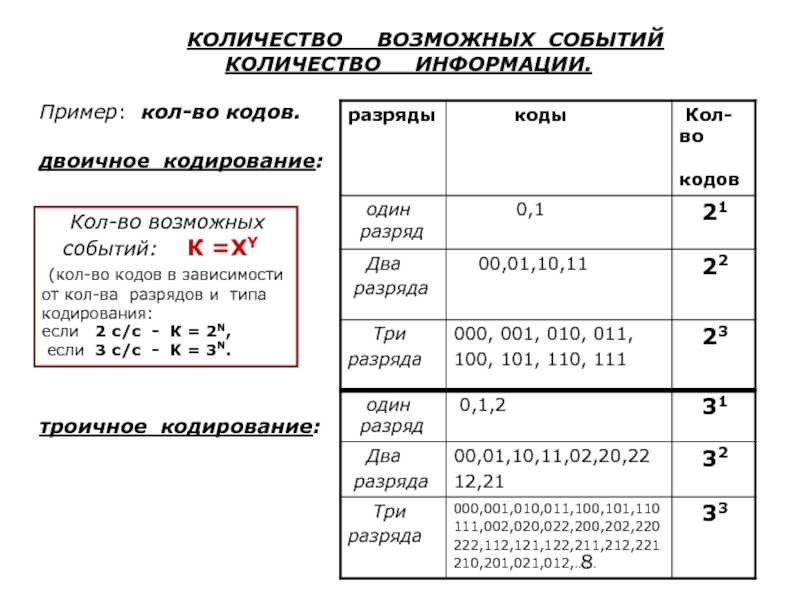
Слайд 8 КОЛИЧЕСТВО ВОЗМОЖНЫХ СОБЫТИЙ
Пример: кол-во кодов.
двоичное кодирование:
троичное кодирование:
Кол-во возможных
событий: К =XY
(кол-во кодов в зависимости от кол-ва разрядов и типа кодирования:
если 2 с/с - К = 2N,
если 3 с/с - K = 3N.
Слайд 10 Алфавитный подход является объективным способом измерения информации в отличие от
Способ, не связывающий количество информации с содержанием сообщения, называется алфавитным подходом.
При алфавитном подходе к измерению информации количество информации зависит от объёма текста и от мощности, а не от содержания.
Мощность алфавита — полное число символов алфавита (N). Каждый символ несёт i бит информации; число i можно определить из уравнения: 2I = N.
Например, мощность алфавита из русских букв и дополнительных символов = 54;
мощность латинского алфавита = 26;
мощность русского алфавита = 33.
Слайд 11
Правило, как измерить информацию, используя для этого
Количество информации, содержащееся в символьном сообщении, равно К · i, где К – число символов в тексте сообщения, а i – информационный вес символа, который находится из уравнения 2I = N, где N – мощность используемого алфавита.
Применение алфавитного подхода удобно при использовании технических средств работы с информацией.
Слайд 12
Например: Каждый символ несёт i бит
Для N = 54 получаем: i = 5,755 бит.
Чтобы найти количество информации во всём тексте, нужно посчитать число символов в нём и умножить на i.
Отсюда следует, что нельзя сравнивать информационные объёмы текстов, написанных на разных языках, только по объёму. У них отличаются информационные веса одного символа так как мощности алфавитов разных языков – различные.
Слайд 13Примеры:
Для передачи секретного сообщения используется код, состоящий из строчных букв латинского
1) 208 бит 2) 750 бит 3) 8 бит 4) 150 байт
2. Для передачи секретного сообщения используется код, состоящий из строчных и прописных букв латинского алфавита. При этом все цифры кодируются одним и тем же (минимально возможным) количеством бит. Определите информационный объем сообщения длиной в 100 символов.
1) 600 бит 2) 500 бит 3) 182 бита 4) 100 байт