- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графики линейных функций презентация
Содержание
- 1. Графики линейных функций
- 2. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Этапы рассмотрения Простейшие примеры
- 3. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Частный случай: прямая пропорциональная
- 4. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Частный случай: меняется свободный член Что происходит с графиком?
- 5. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Первые гипотезы Связь
- 6. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Скорость роста – «крутизна»
- 7. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Взаимное расположение двух графиков
- 8. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Взаимное расположение двух графиков
- 9. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Построить семейство графиков линейных
- 10. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Построить семейство графиков линейных
- 11. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Эксперимент: Более сложные семейства
- 12. ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ Эксперимент: Более сложные семейства
Слайд 2ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
Этапы рассмотрения
Простейшие примеры
Свойства графиков линейных функций
Графики и коэффициенты
Пересечения графиков и системы
Динамические демонстрации
Слайд 3ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
Частный случай: прямая пропорциональная зависимость
Как форма графика связана со
Слайд 5ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
Первые гипотезы
Связь формы графика с коэффициентами:
График линейной функции –
При изменении коэффициента при х меняется «крутизна» графика.
При изменении свободного члена происходит параллельный перенос графика.
Слайд 6ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
Скорость роста – «крутизна» графика
у = 2х + 1 Таблица
Вывод: постоянному приращению аргумента Δх
соответствует постоянное приращение функции Δу
Слайд 7ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
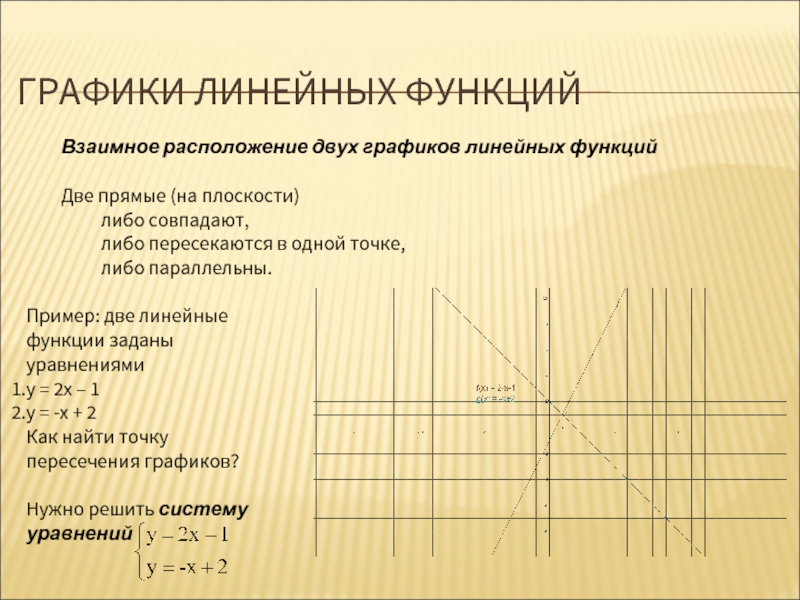
Взаимное расположение двух графиков линейных функций
Две прямые (на плоскости)
Пример: две линейные функции заданы уравнениями
у = 2х – 1
у = -х + 2
Как найти точку пересечения графиков?
Нужно решить систему уравнений
Слайд 8ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
Взаимное расположение двух графиков линейных функций – случай параллельных
Решим соответствующую систему:
Вычтем из первого уравнения второе.
Мы снова приходим к трем случаям:
Если k1 = k2 и b1 = b2, тогда уравнение имеет бесконечно много решений (функции одинаковы, графики совпадают).
Если k1 = k2 и b1 ≠ b2, тогда уравнение не имеет решений (графики параллельны).
Если k1 ≠ k2 и b1 ≠ b2, тогда уравнение имеет единственное решение (графики пересекаются в одной точке).
Слайд 9ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
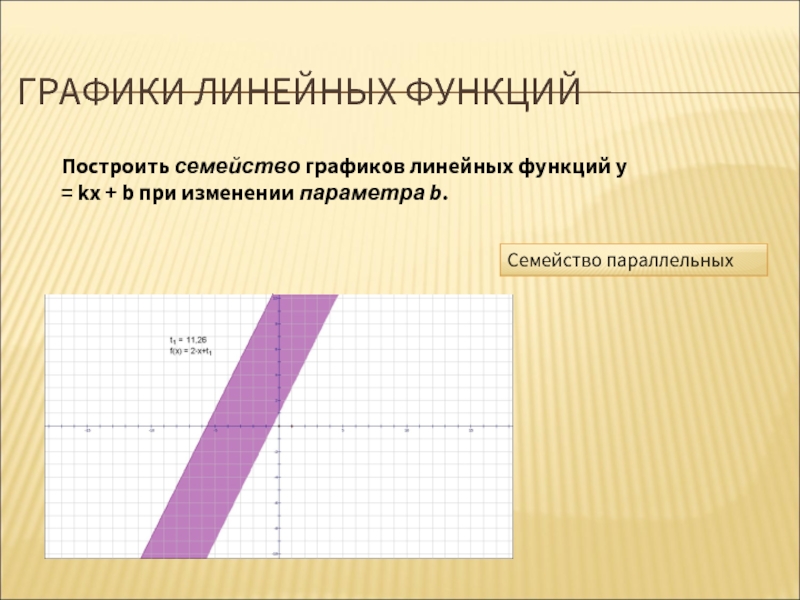
Построить семейство графиков линейных функций у = kх +
Семейство параллельных
Слайд 10ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
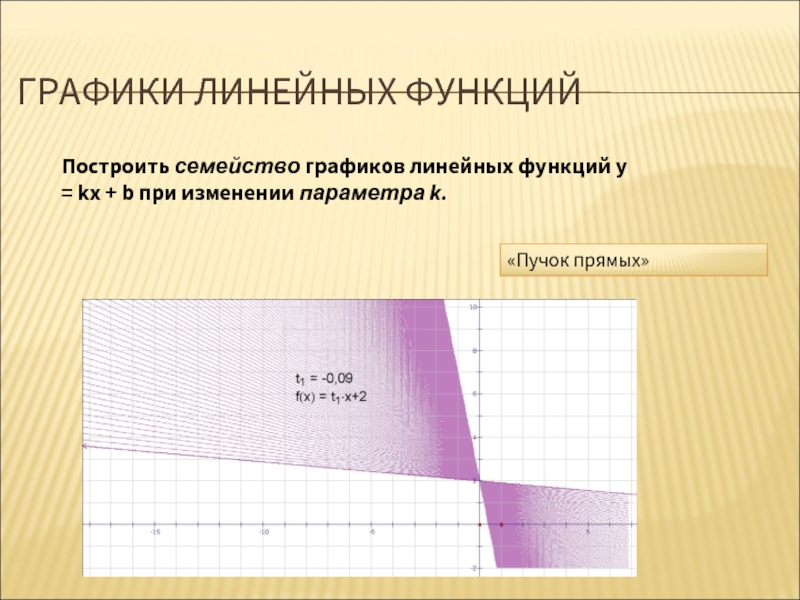
Построить семейство графиков линейных функций у = kх +
«Пучок прямых»
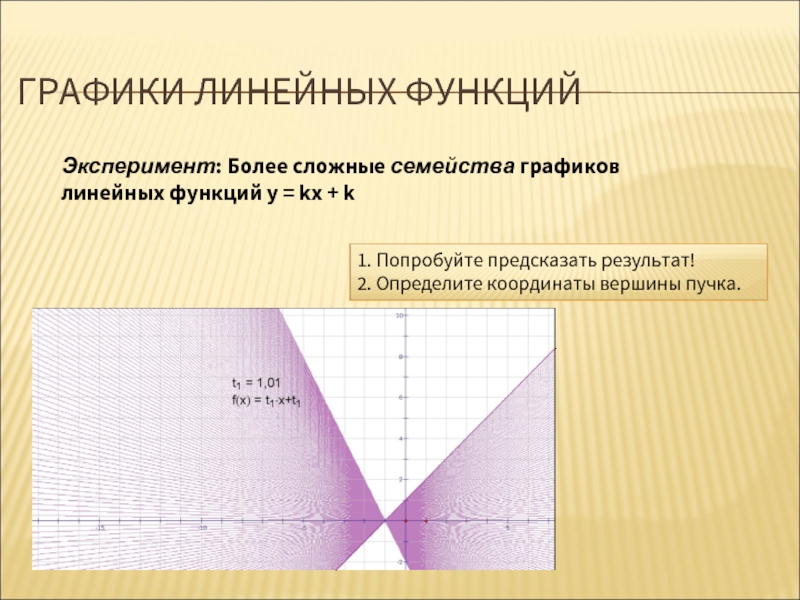
Слайд 11ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
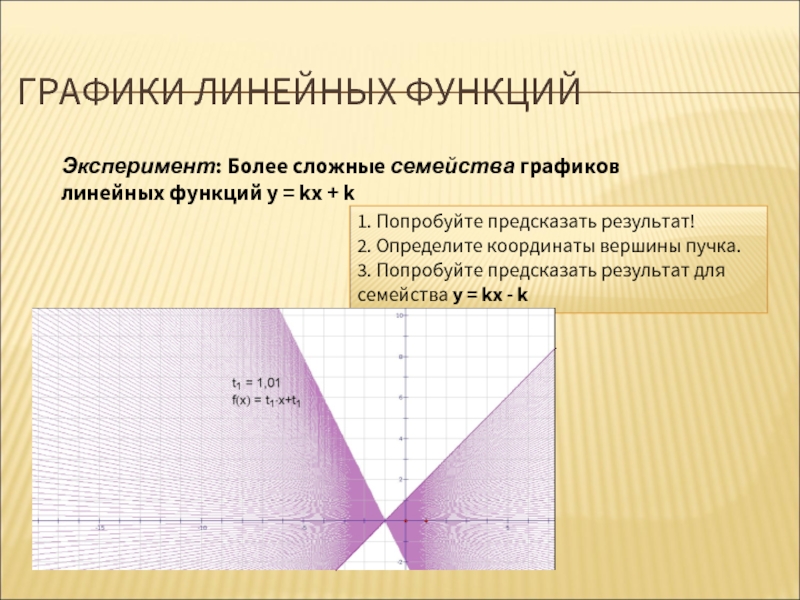
Эксперимент: Более сложные семейства графиков линейных функций у =
1. Попробуйте предсказать результат!
2. Определите координаты вершины пучка.
3. Попробуйте предсказать результат для семейства у = kх - k
Слайд 12ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ
Эксперимент: Более сложные семейства графиков линейных функций у =
1. Попробуйте предсказать результат!
2. Определите координаты вершины пучка.