- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические построенияциркулем и линейкой презентация
Содержание
- 1. Геометрические построенияциркулем и линейкой
- 2. Выполнил: Цун Иосиф Менделевич, профессор кафедры алгебры
- 3. Основное построение № 1 Отложить на данном
- 4. Основное построение № 2 Отложить от данного
- 5. Основное построение № 3 Построить треугольник по
- 6. Основное построение № 4 Построить треугольник по
- 7. Основное построение № 5 Построить треугольник по
- 8. Основное построение № 6 Построить биссектрису данного
- 9. Основное построение № 7 Построить серединный перпендикуляр
- 10. Основное построение № 8 Построить прямую, проходящую
- 11. Основное построение № 8 Построить прямую, проходящую
- 12. Основное построение № 9 Построить прямую, проходящую
- 13. Основное построение № 9 Построить прямую, проходящую
- 14. Основное построение № 10 Построить прямоугольный треугольник
- 15. Основное построение № 11 Построить прямоугольный треугольник
- 16. Основное построение № 12 Для окружности построить
- 17. Основное построение № 12 Для окружности построить
- 18. Основное построение № 13 Построение четвертого пропорционального
- 19. Благодарю за внимание
Слайд 2Выполнил:
Цун Иосиф Менделевич,
профессор кафедры
алгебры и геометрии МаГУ,
кандидат технических наук
E-mail: tsoun@masu.ru
http://im-ts.narod.ru
Слайд 3Основное построение № 1
Отложить на данном луче от его начала отрезок,
a
S
A
F
Построение:
Циркулем измеряем отрезок a.
Дано:
С центром в точке S проводим дугу радиуса SA = a.
SA – искомый отрезок.
а
Слайд 4Основное построение № 2
Отложить от данного луча в данную полуплоскость угол,
Построение:
Дано:
С центром в точке О проводим дугу произвольного радиуса, пересекающую стороны угла в точках М и N.
A
B
N
M
α
F
N′
α
M′
O
S
С центром в точке S тем же радиусом проводим дугу в заданной полуплоскости. Пусть она пересекает SF в точке N′.
Циркулем измеряем MN и откладываем от N′ на построенной ранее дуге с центром в точке S. Получаем M′.
Проводим луч SM′. Угол M′SN′ – искомый.
Слайд 5Основное построение № 3
Построить треугольник по трём сторонам.
На произвольной прямой откладываем
Построение:
Дано:
a
b
c
A
B
C
c
b
a
С центром в точке А строим дугу радиусом b.
С центром в точке В – дугу радиусом а.
Пересечение дуг дает точку С – вершину искомого треугольника.
Проводим отрезки b = AC и a = BC. Треугольник ABC – искомый.
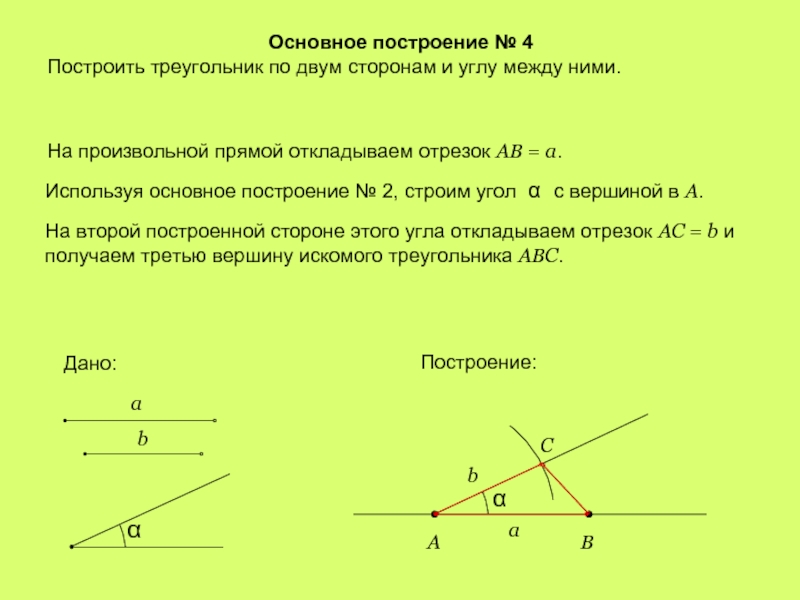
Слайд 6Основное построение № 4
Построить треугольник по двум сторонам и углу между
На произвольной прямой откладываем отрезок АВ = a.
Построение:
Дано:
a
b
α
A
B
C
b
a
α
Используя основное построение № 2, строим угол α с вершиной в А.
На второй построенной стороне этого угла откладываем отрезок АC = b и получаем третью вершину искомого треугольника ABC.
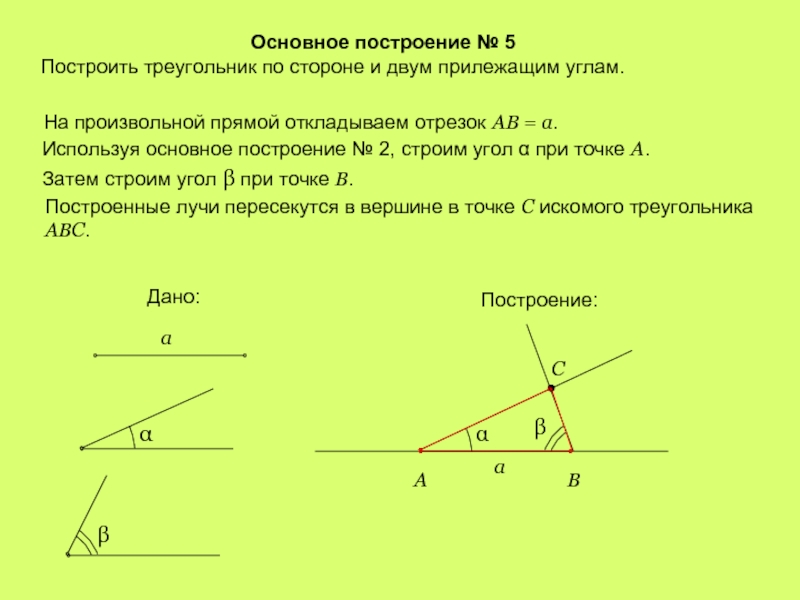
Слайд 7Основное построение № 5
Построить треугольник по стороне и двум прилежащим углам.
На
Дано:
a
α
β
α
A
B
C
a
β
Построение:
Используя основное построение № 2, строим угол α при точке A.
Затем строим угол β при точке В.
Построенные лучи пересекутся в вершине в точке С искомого треугольника АВС.
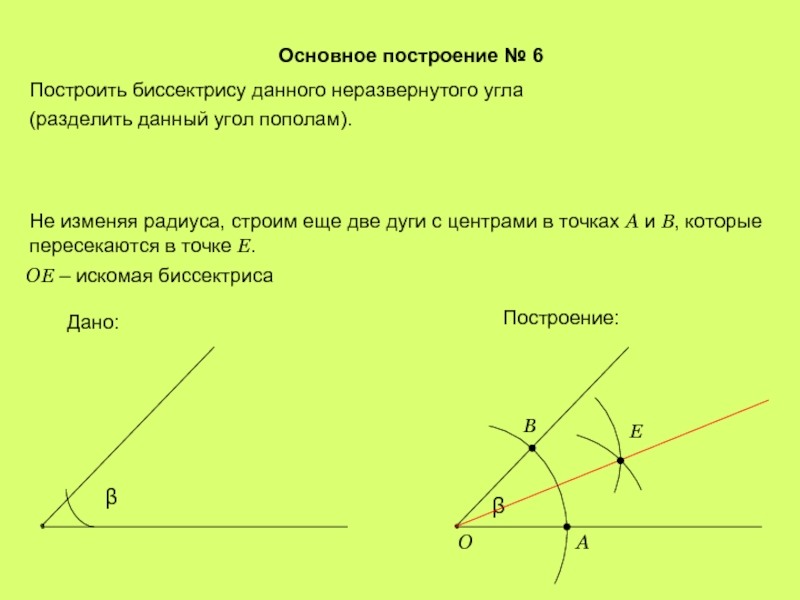
Слайд 8Основное построение № 6
Построить биссектрису данного неразвернутого угла
(разделить данный угол пополам).
Построение:
β
B
A
E
Дано:
β
Не
О
ОЕ – искомая биссектриса
Слайд 9Основное построение № 7
Построить серединный перпендикуляр данного отрезка
(аналогично выполняется построение середины
С центрами в точках А и В и радиусом, большим половины отрезка АВ, строим две дуги, пересекающиеся в точках С и D.
Построение:
A
B
C
D
O
Дано:
A
B
CD – искомый серединный перпендикуляр.
О – середина данного отрезка АВ.
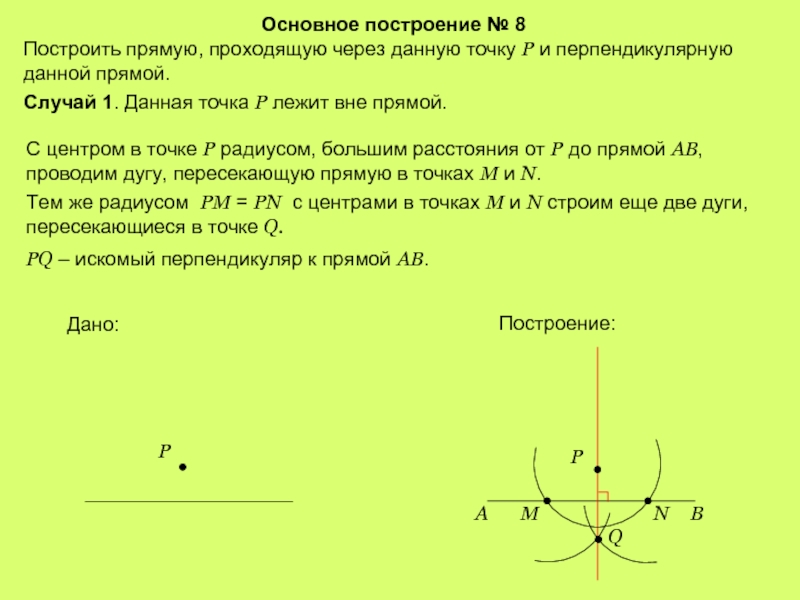
Слайд 10Основное построение № 8
Построить прямую, проходящую через данную точку Р и
Случай 1. Данная точка P лежит вне прямой.
С центром в точке Р радиусом, большим расстояния от Р до прямой АВ, проводим дугу, пересекающую прямую в точках М и N.
A
B
M
N
P
Q
Построение:
P
Дано:
Тем же радиусом PM = PN с центрами в точках М и N строим еще две дуги, пересекающиеся в точке Q.
PQ – искомый перпендикуляр к прямой АВ.
Слайд 11Основное построение № 8
Построить прямую, проходящую через данную точку Р и
Случай 2. Данная точка P лежит на прямой.
С центром в точке Р произвольным радиусом проводим дугу, пересекающую прямую в точках М и N.
N
M
C
D
P
A
B
Построение:
Дано:
С центрами в точках М и N строим ещё две дуги равного радиуса и большего, чем расстояние до точки P.
Через точки C и D пересечения этих дуг проводим прямую. CD – искомый перпендикуляр к прямой АВ в точке Р.
P
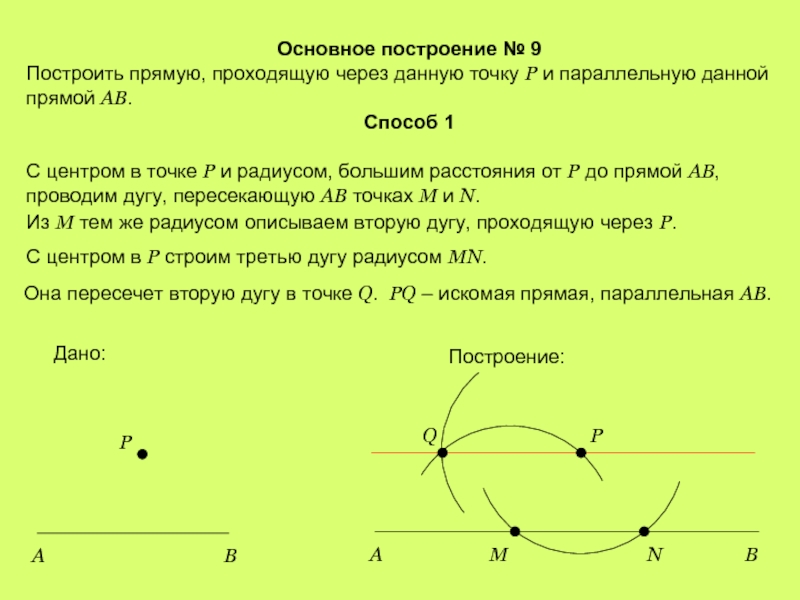
Слайд 12Основное построение № 9
Построить прямую, проходящую через данную точку Р и
Способ 1
Построение:
С центром в точке Р и радиусом, большим расстояния от Р до прямой АВ, проводим дугу, пересекающую АВ точках М и N.
P
M
N
Q
P
А
В
Дано:
Из M тем же радиусом описываем вторую дугу, проходящую через Р.
Она пересечет вторую дугу в точке Q. PQ – искомая прямая, параллельная AB.
A
B
С центром в Р строим третью дугу радиусом МN.
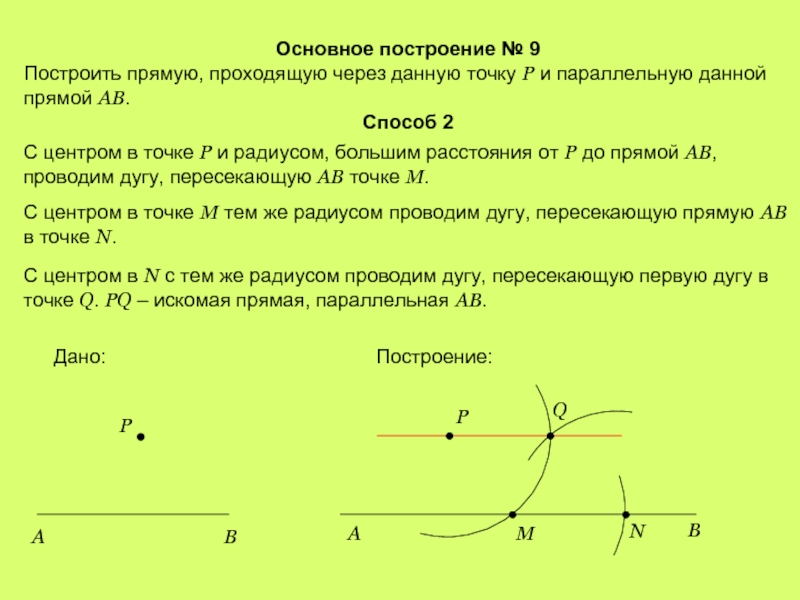
Слайд 13Основное построение № 9
Построить прямую, проходящую через данную точку Р и
Способ 2
С центром в точке Р и радиусом, большим расстояния от Р до прямой АВ, проводим дугу, пересекающую АВ точке М.
Построение:
P
M
N
Q
P
А
В
Дано:
А
В
С центром в точке М тем же радиусом проводим дугу, пересекающую прямую АВ в точке N.
С центром в N с тем же радиусом проводим дугу, пересекающую первую дугу в точке Q. PQ – искомая прямая, параллельная AB.
Слайд 14Основное построение № 10
Построить прямоугольный треугольник по гипотенузе и острому углу.
На
Дано:
a
α
Построение:
α
A
B
C
a
Далее строим угол, равный данному углу α, с вершиной в А.
На другую сторону угла опускаем перпендикуляр из второго конца гипотенузы – точки В.
Получаем вершину С прямого угла искомого треугольника АВС.
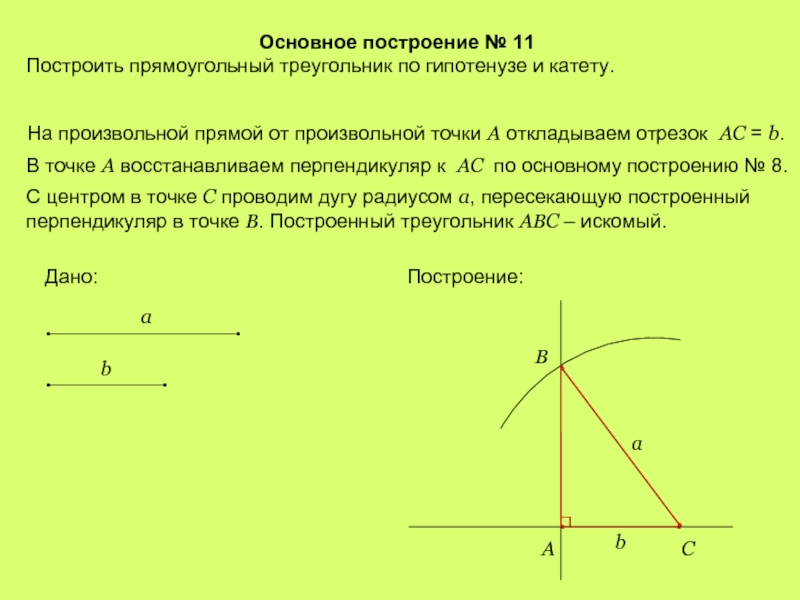
Слайд 15Основное построение № 11
Построить прямоугольный треугольник по гипотенузе и катету.
На произвольной
Дано:
a
b
Построение:
A
b
C
B
a
В точке А восстанавливаем перпендикуляр к АС по основному построению № 8.
С центром в точке С проводим дугу радиусом а, пересекающую построенный перпендикуляр в точке В. Построенный треугольник АВС – искомый.
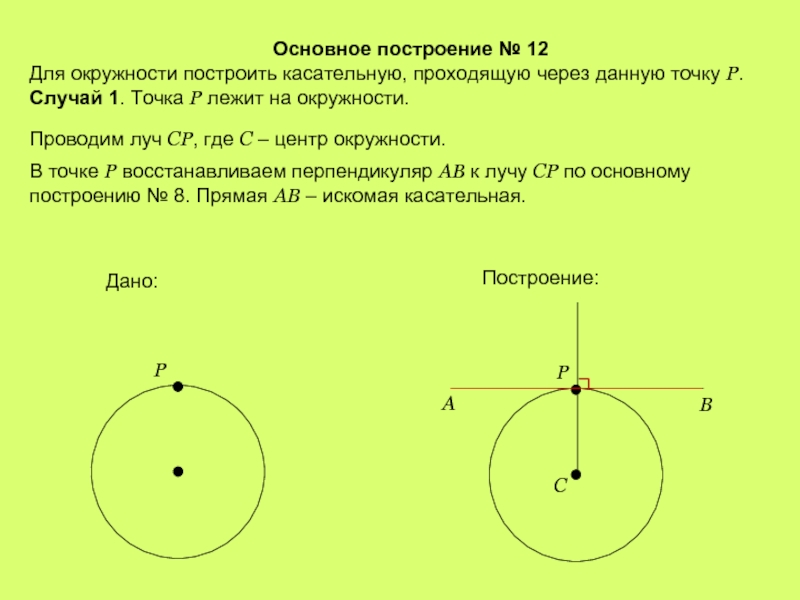
Слайд 16Основное построение № 12
Для окружности построить касательную, проходящую через данную точку
Случай 1. Точка Р лежит на окружности.
Проводим луч СР, где С – центр окружности.
С
P
A
B
Построение:
P
Дано:
В точке Р восстанавливаем перпендикуляр АВ к лучу СР по основному построению № 8. Прямая АВ – искомая касательная.
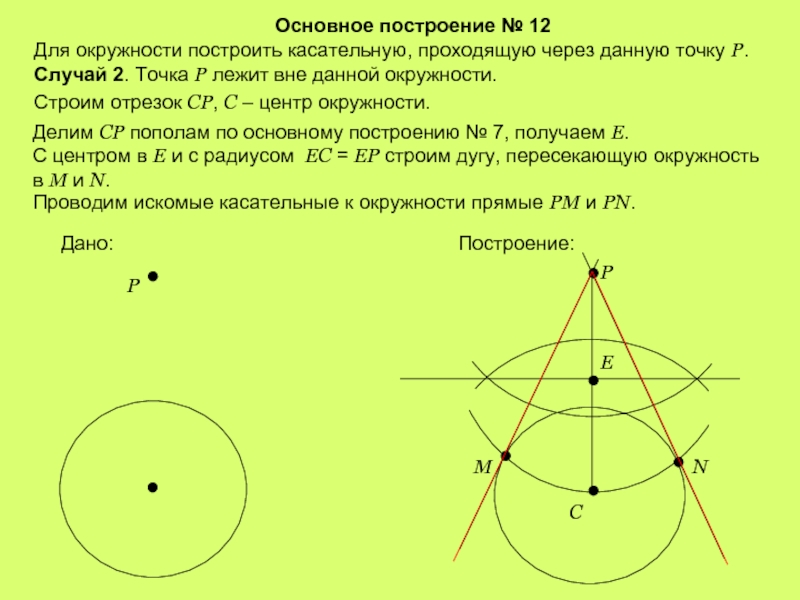
Слайд 17Основное построение № 12
Для окружности построить касательную, проходящую через данную точку
Случай 2. Точка Р лежит вне данной окружности.
С
P
Строим отрезок СР, С – центр окружности.
Построение:
M
N
E
Делим СР пополам по основному построению № 7, получаем Е.
Проводим искомые касательные к окружности прямые PM и PN.
Дано:
P
С центром в Е и с радиусом ЕС = ЕР строим дугу, пересекающую окружность в М и N.
Слайд 18Основное построение № 13
Построение четвертого пропорционального отрезка x.
Строим произвольный угол, на
O
B
A
C
X
Дано:
a
b
c
Построение:
c
a
b
x
На той же стороне угла, что и a, откладываем AС = с.
Через точку C проводим прямую, параллельную АB, которая пересекает на луче ОB искомый отрезок х. Отрезок BХ = х – искомый.