- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Генетические алгоритмы презентация
Содержание
- 1. Генетические алгоритмы
- 2. Формальное определение Генетический алгоритм — это
- 3. Зачем нужны ГА? Генетические алгоритмы применяются
- 4. Ключевые работы Родителем современной теории генетических
- 5. Принцип работы ГА Популяция –
- 6. Схема работы любого ГА Шаг алгоритма
- 7. Применение генетических алгоритмов в задачах оптимизации – поиска минимума функции Швефеля
- 8. Были разработаны специальные функции для тестирования различных
- 10. На плоскости XY под трёхмерным графиком находится
- 12. По графикам видно, что почти всё поле
Слайд 2
Формальное определение
Генетический алгоритм — это алгоритм, который позволяет найти удовлетворительное решение
к аналитически неразрешимым проблемам через последовательный подбор и комбинирование искомых параметров с использованием механизмов, напоминающих биологическую эволюцию.
Слайд 3
Зачем нужны ГА?
Генетические алгоритмы применяются для решения следующих задач:
Оптимизация функций
Разнообразные
задачи на графах (задача коммивояжера, раскраска, нахождение паросочетаний)
Настройка и обучение искусственной нейронной сети
Составление расписаний
Игровые стратегии
Аппроксимация функций
Искусственная жизнь
Биоинформатика
Настройка и обучение искусственной нейронной сети
Составление расписаний
Игровые стратегии
Аппроксимация функций
Искусственная жизнь
Биоинформатика
Слайд 4
Ключевые работы
Родителем современной теории генетических алгоритмов считается Д.Х. Холланд (J. Holland). Однако
сначала его интересовала, прежде всего, способность природных систем к адаптации, а его мечтой было создание такой системы, которая могла бы приспосабливаться к любым условиям окружающей среды.
В 1975 году Холланд публикует свою самую знаменитую работу «Adaptation in Natural and Artificial Systems».В ней он впервые ввёл термин «генетический алгоритм» и предложил схему классического генетического алгоритма (canonical GA). В дальнейшем понятие «генетические алгоритмы» стало очень широким, и зачастую к ним относятся алгоритмы, сильно отличающиеся от классического ГА.
Ученики Холланда - Кеннет Де Йонг (Kenneth De Jong) и Дэвид Голдберг (David E. Goldberg) - внесли огромный вклад в развитие ГА. Наиболее известная работа Голдберга - «Genetic algorithms in search optimization and machine learning» (1989).
В 1975 году Холланд публикует свою самую знаменитую работу «Adaptation in Natural and Artificial Systems».В ней он впервые ввёл термин «генетический алгоритм» и предложил схему классического генетического алгоритма (canonical GA). В дальнейшем понятие «генетические алгоритмы» стало очень широким, и зачастую к ним относятся алгоритмы, сильно отличающиеся от классического ГА.
Ученики Холланда - Кеннет Де Йонг (Kenneth De Jong) и Дэвид Голдберг (David E. Goldberg) - внесли огромный вклад в развитие ГА. Наиболее известная работа Голдберга - «Genetic algorithms in search optimization and machine learning» (1989).
Слайд 5
Принцип работы ГА
Популяция – совокупностью всех «особей», представляющих собой строки, кодирующие
одно из решений задачи.
С помощью функции приспособленности:
наиболее приспособленные (более подходящие решения) получают возможность скрещиваться и давать потомство
наихудшие (плохие решения) удаляются из популяции и не дают потомства
Таким образом, приспособленность нового поколения в среднем выше предыдущего.
В классическом ГА:
начальная популяция формируется случайным образом
размер популяции (количество особей N) фиксируется и не изменяется в течение работы всего алгоритма
каждая особь генерируется как случайная L-битная строка, где L — длина кодировки особи
длина кодировки для всех особей одинакова
С помощью функции приспособленности:
наиболее приспособленные (более подходящие решения) получают возможность скрещиваться и давать потомство
наихудшие (плохие решения) удаляются из популяции и не дают потомства
Таким образом, приспособленность нового поколения в среднем выше предыдущего.
В классическом ГА:
начальная популяция формируется случайным образом
размер популяции (количество особей N) фиксируется и не изменяется в течение работы всего алгоритма
каждая особь генерируется как случайная L-битная строка, где L — длина кодировки особи
длина кодировки для всех особей одинакова
Слайд 6
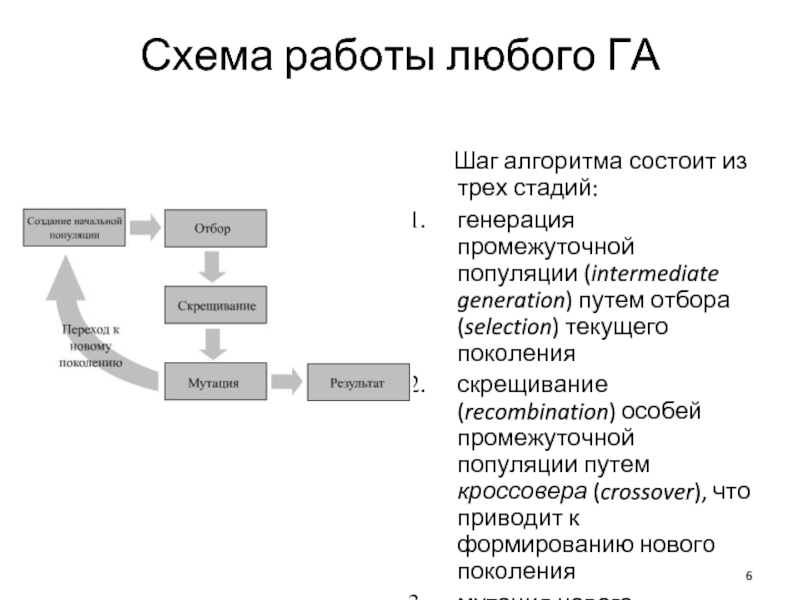
Схема работы любого ГА
Шаг алгоритма состоит из трех стадий:
генерация промежуточной популяции
(intermediate generation) путем отбора (selection) текущего поколения
скрещивание (recombination) особей промежуточной популяции путем кроссовера (crossover), что приводит к формированию нового поколения
мутация нового поколения
скрещивание (recombination) особей промежуточной популяции путем кроссовера (crossover), что приводит к формированию нового поколения
мутация нового поколения
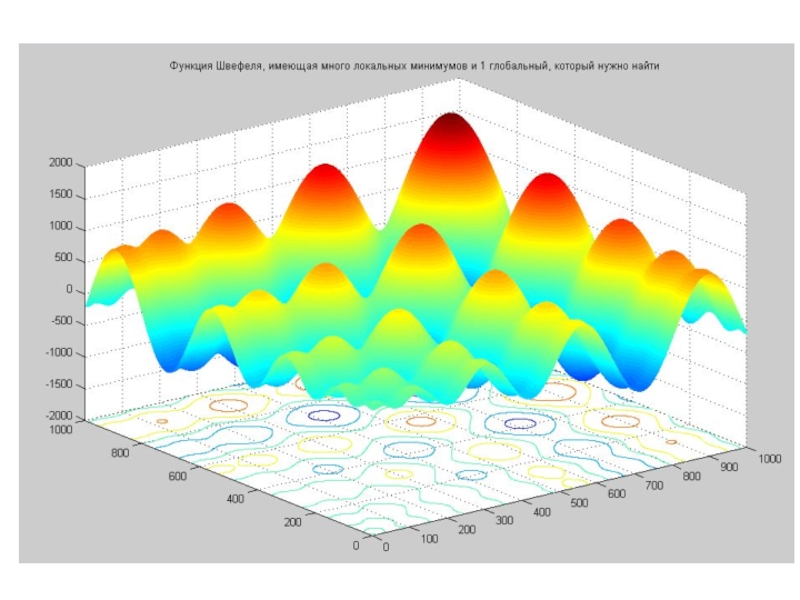
Слайд 8Были разработаны специальные функции для тестирования различных оптимизационных алгоритмов. Такие функции
характеризуются множеством локальных минимумов и одним глобальным. Задача состоит в том, чтобы найти этот глобальный минимум и при этом не застрять в одном из локальных минимумов.
В качестве такой функции примем функцию Ханс-Пауля Швефеля, предложенную им в своей работе 1977 года.
В оригинальной работе она выражена так:
Здесь аргументов функции может быть множество – это многокритериальная оптимизация. Для геометрической интерпретации поиска примем эту функцию от двух аргументов, так как большее количество аргументов уже не представимо графически в нашем трёхмерном пространстве.
Трёхмерная поверхность этой функции имеет следующий вид:
В качестве такой функции примем функцию Ханс-Пауля Швефеля, предложенную им в своей работе 1977 года.
В оригинальной работе она выражена так:
Здесь аргументов функции может быть множество – это многокритериальная оптимизация. Для геометрической интерпретации поиска примем эту функцию от двух аргументов, так как большее количество аргументов уже не представимо графически в нашем трёхмерном пространстве.
Трёхмерная поверхность этой функции имеет следующий вид:
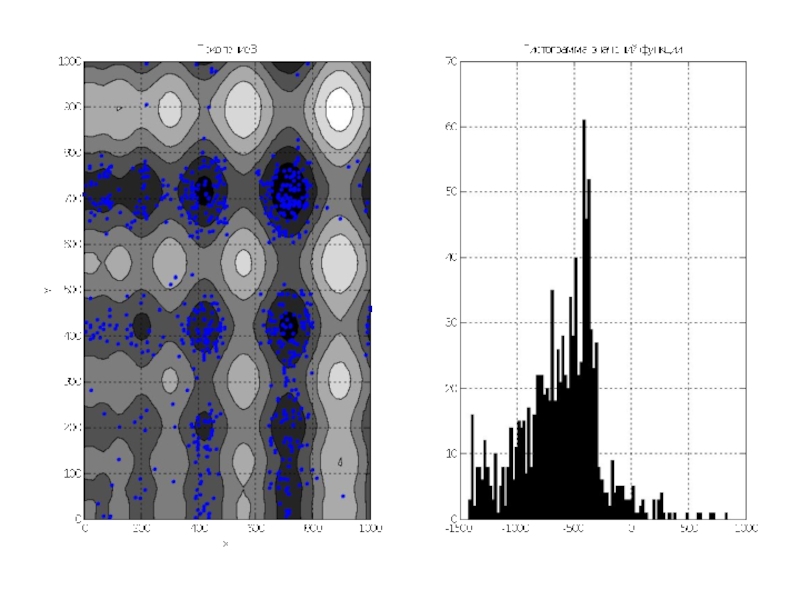
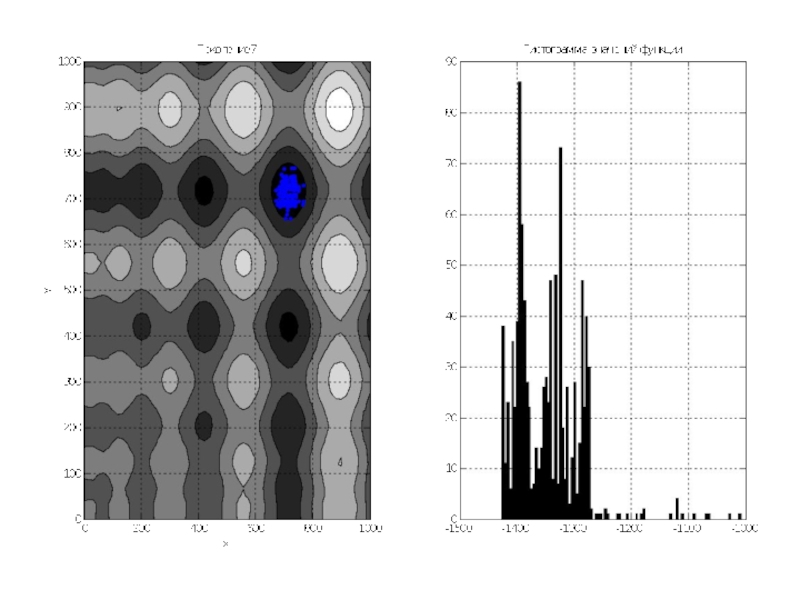
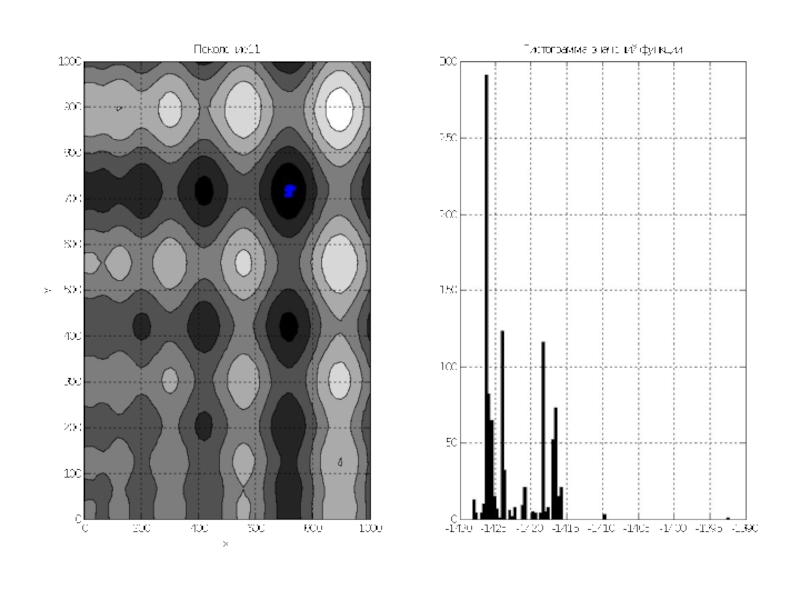
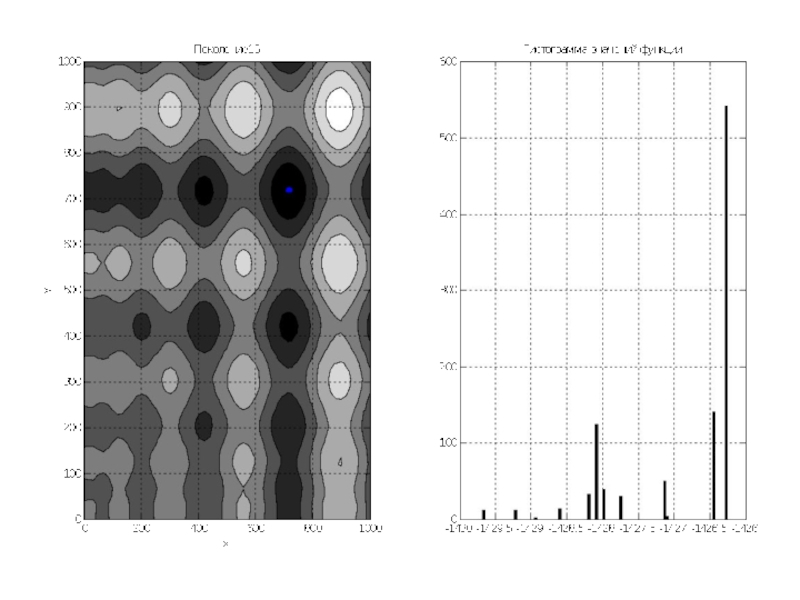
Слайд 10На плоскости XY под трёхмерным графиком находится контурный график с изображёнными
линиями одинакового уровня.
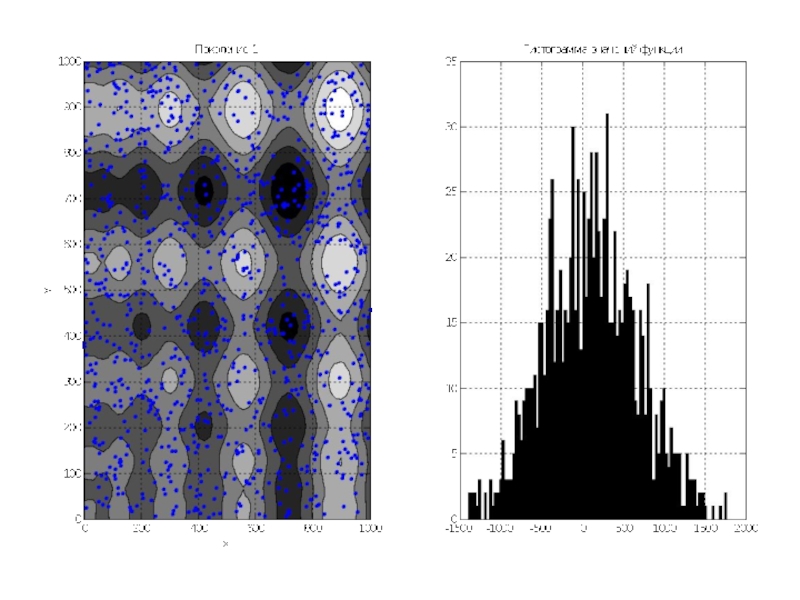
Для дальнейшей работы строим плоский график этих уровней, причём раскрашиваем его в серые тона, где более тёмные места означают меньшие значения функции.
Затем на этот график накладываются точки особей популяции в количестве 1000 особей. Это начальная популяция – поколение №1.
Рядом с этим графиком строится гистограмма распределения значений функции по популяции.
Затем для каждой особи популяции вычисляется целевая функция – это значение функции. По величине целевой функции сортируется популяция. Верхние 500 особей с меньшими значениями будут родителями, а 500 нижних не выживут и не перейдут в следующее поколение. Их места займут дети верхних особей.
Затем кроссовер между родителями, и родители вместе с детьми составляют поколение №2.
После этого к каждой особи нового поколения применяется оператор мутации с вероятностью 3%.
Затем также осуществляется отбор и далее аналогично.
Для дальнейшей работы строим плоский график этих уровней, причём раскрашиваем его в серые тона, где более тёмные места означают меньшие значения функции.
Затем на этот график накладываются точки особей популяции в количестве 1000 особей. Это начальная популяция – поколение №1.
Рядом с этим графиком строится гистограмма распределения значений функции по популяции.
Затем для каждой особи популяции вычисляется целевая функция – это значение функции. По величине целевой функции сортируется популяция. Верхние 500 особей с меньшими значениями будут родителями, а 500 нижних не выживут и не перейдут в следующее поколение. Их места займут дети верхних особей.
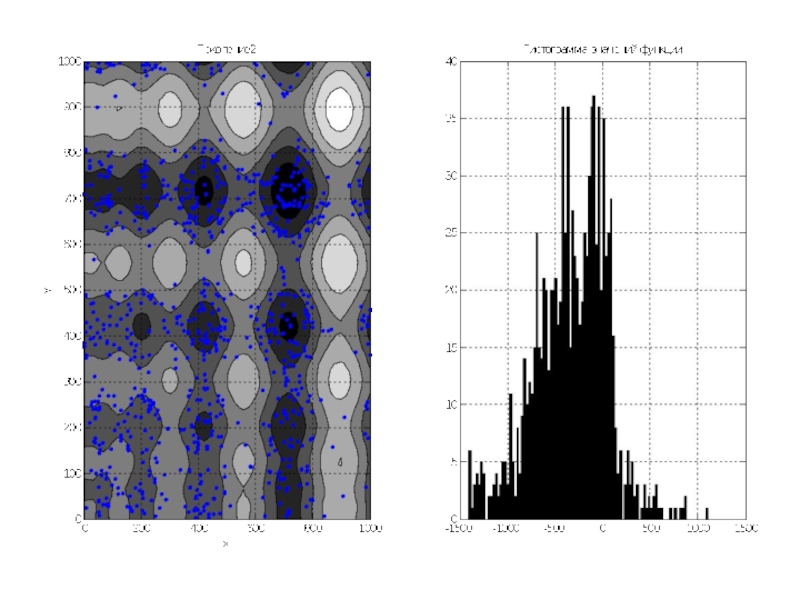
Затем кроссовер между родителями, и родители вместе с детьми составляют поколение №2.
После этого к каждой особи нового поколения применяется оператор мутации с вероятностью 3%.
Затем также осуществляется отбор и далее аналогично.
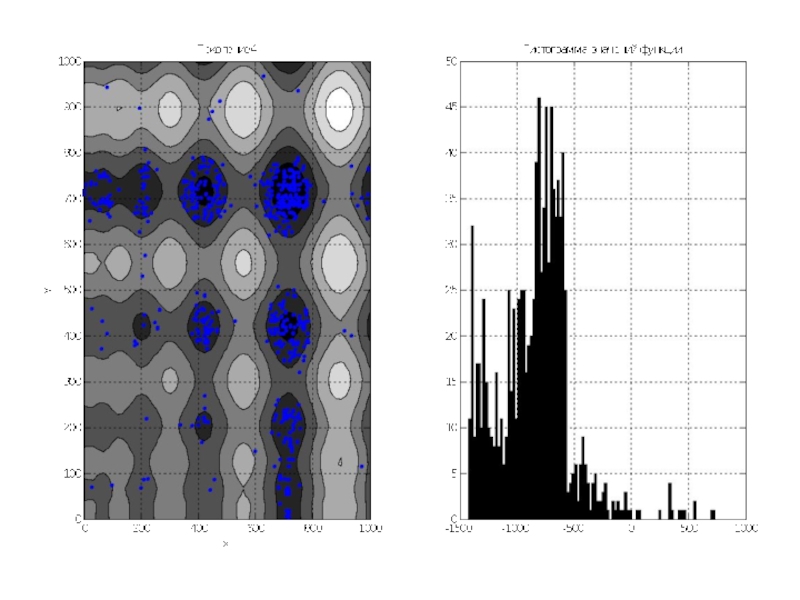
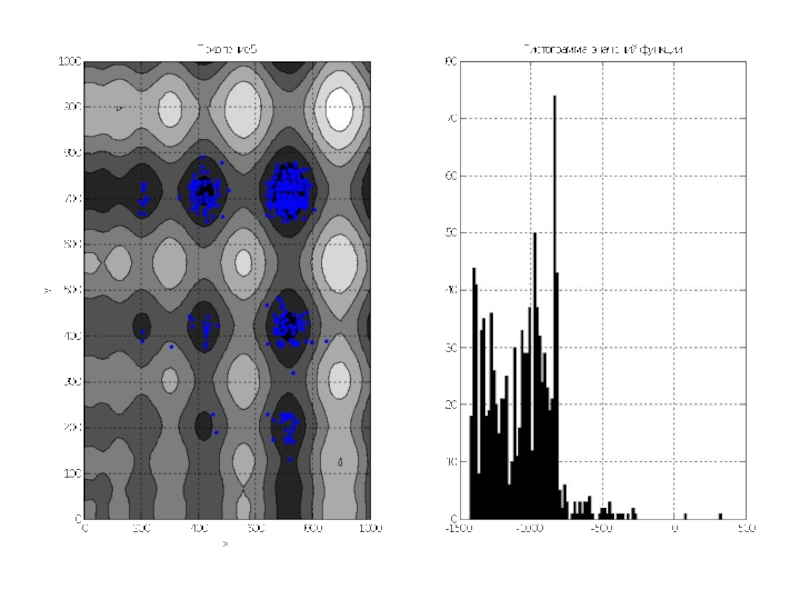
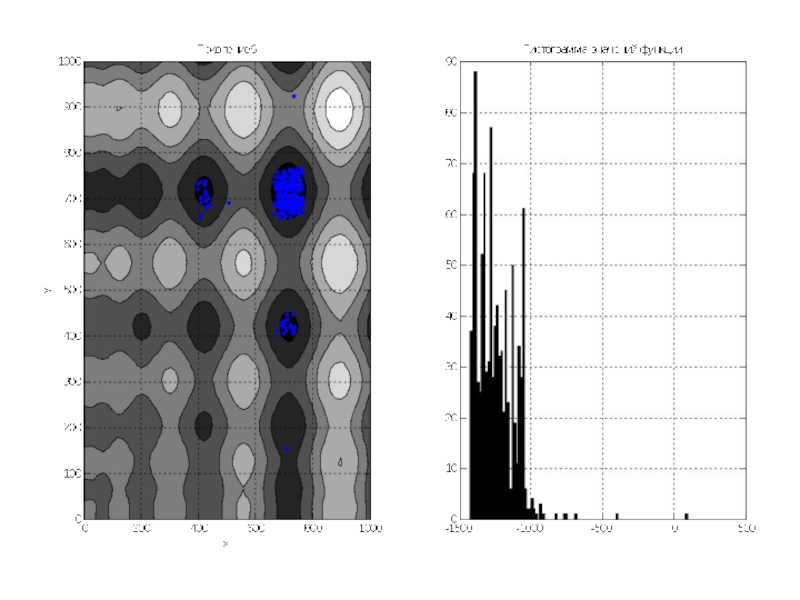
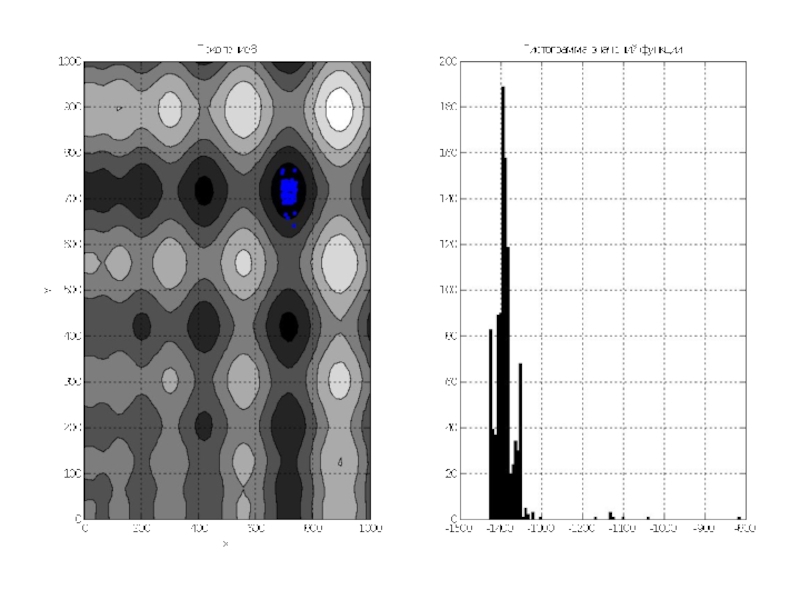
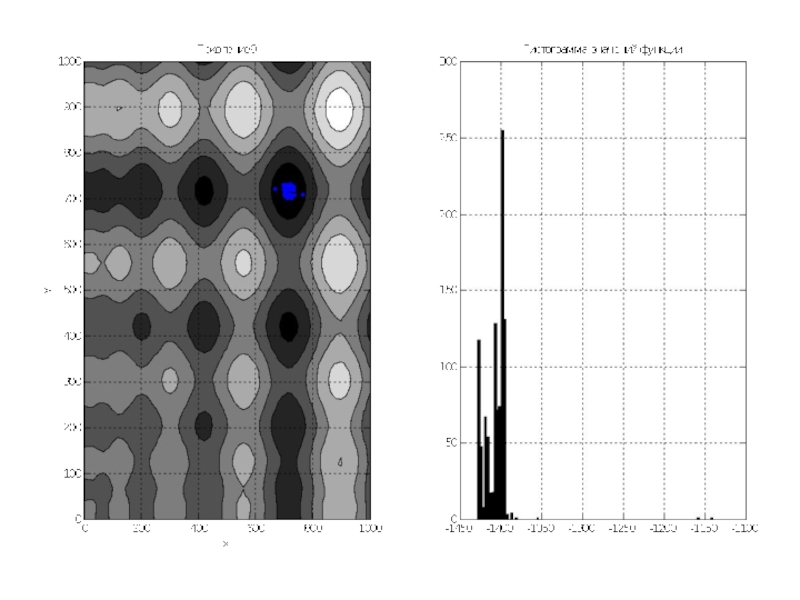
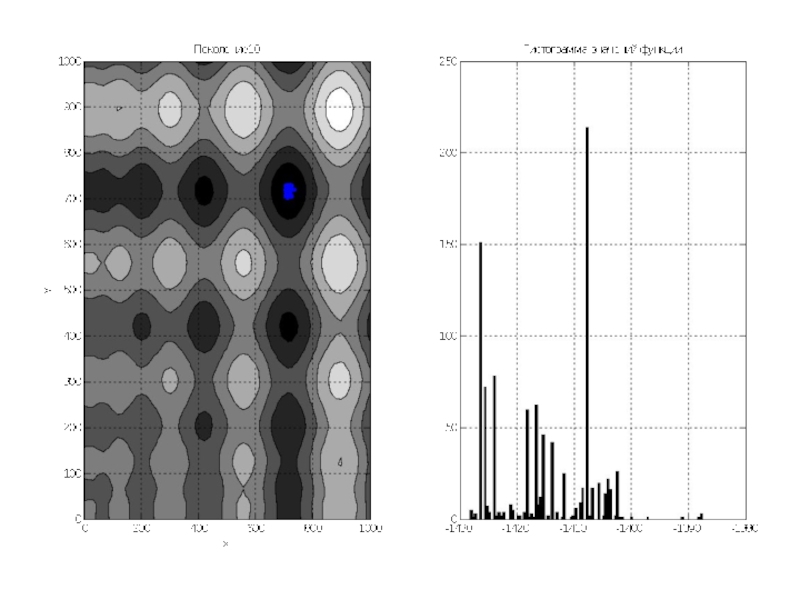
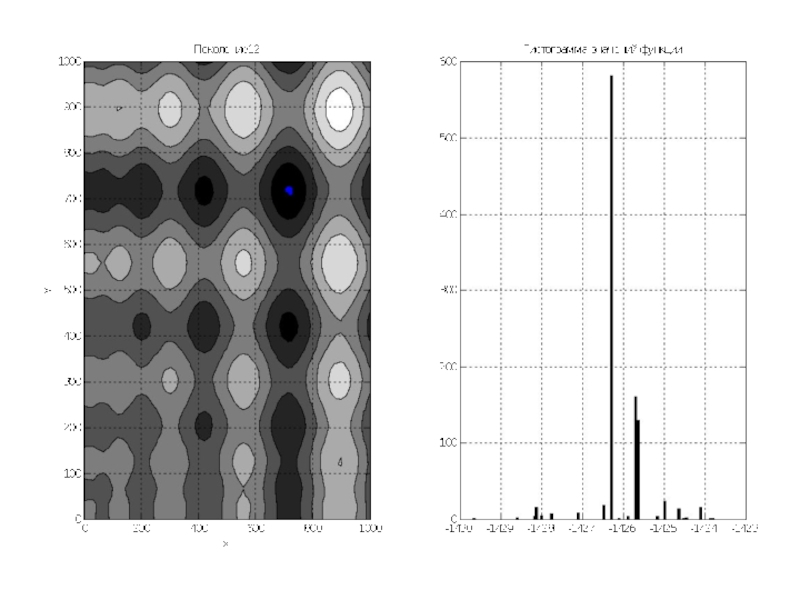
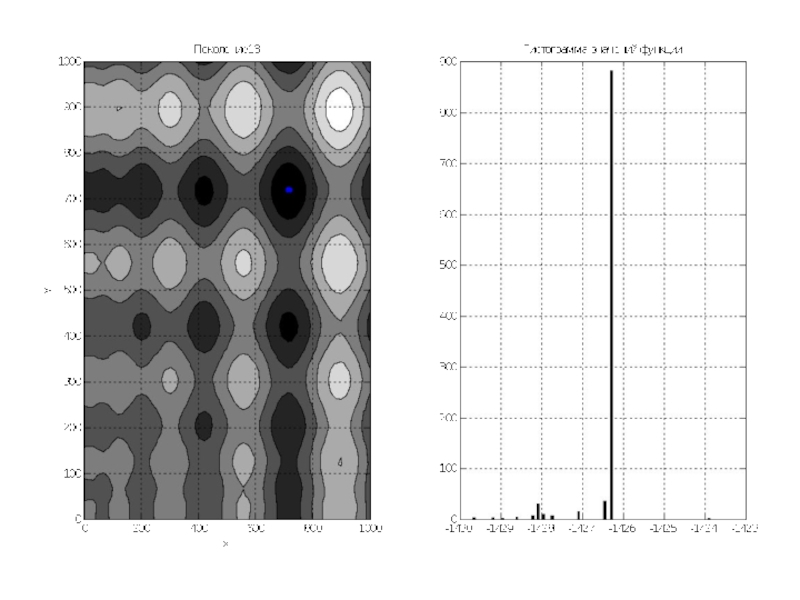
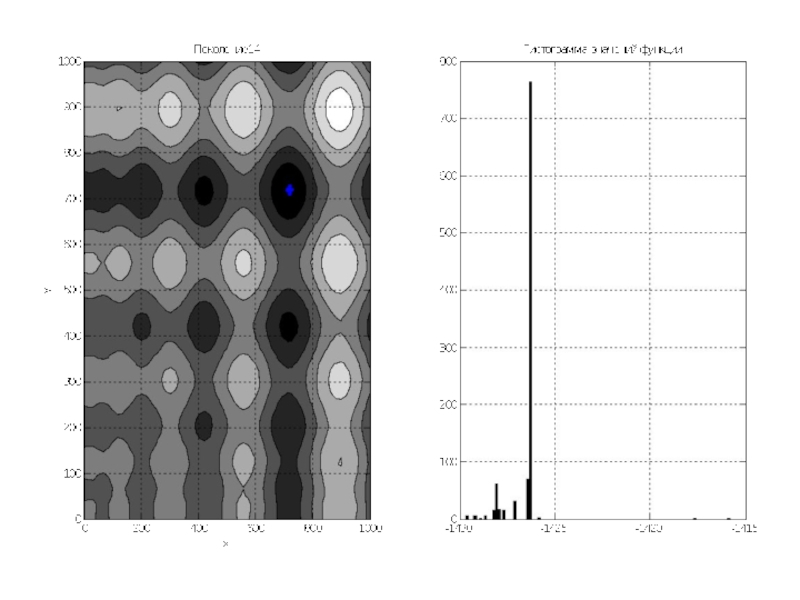
Слайд 12По графикам видно, что почти всё поле покрыто точками особей. Гистограмма
показывает, что математическое ожидание около 0, так как функция симметрична относительно 0, и значения её простираются примерно от -1500 до 1500.
Переходим к последующим поколениям.
Переходим к последующим поколениям.