- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физические основы технологических процессов презентация
Содержание
- 1. Физические основы технологических процессов
- 2. Лекция №1 Основными задачами дисциплины «Физические основы
- 3. Физические процессы разнообразных металлургических и машиностроительных технологий
- 4. Следуя традициям, заложенным в теоретической механике, основными
- 5. Влияние условий деформирования на сопротивление материалов
- 6. для свинца, имеющего температуру плавления Тпл=600 К
- 7. Гипотеза о постоянстве удельных касательных сил при резании
- 8. Простое нагружение, теория течения Пластические деформации вызывают
- 9. по Н.Н.Зореву по М.Ф.Полетике и
- 10. Влияние температуры на предел прочности стали
- 11. . Влияние температуры на средний предел
- 12. Влияние скорости деформации при растяжении
- 13. резание сталей 00, 10, 20Х,
- 14. Сопротивление материалов большим пластическим деформациям в адиабатических условиях деформирования
- 15. Удельная работа деформации Гипотеза
- 16. Влияние локализации деформаций в узкой зоне на
- 17. Кривая течения для
- 18. Действительные характеристики сопротивления материала пластическим деформациям
- 19. Влияние локализации деформаций на кривую течения
- 20. СИЛЫ РЕЗАНИЯ Схема технологических осей
- 21. Зависимости удельных сил резания от удельных
- 22. Удельные силы резания на передней поверхности
- 23. Теоретическое определение усадки при постоянных касательных напряжениях
- 24. схема технологических составляющих силы при свободном прямоугольном точении
- 25. Влияние ширины фаски износа на силы
- 26. Расчет сил при свободном прямоугольном точении
- 27. Напряжения в клине под действием сосредоточенной силы,
- 28. Силы на передней поверхности
- 29. В системе координат ξ1,ν1, повернутой на угол
- 30. Силы на задней поверхности в координатах ξ,ν:
- 31. Наибольшие касательные напряжения на поверхности
- 32. радиальное напряжение при θ=π/2,
- 33. Наиболее благоприятными значениями ширины фаски износа и
- 34. ВЛИЯНИЕ толщины среза и радиальной силы Р2 на округление режущей кромки при :
- 35. ТЕПЛОФИЗИКА ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ три основных
- 36. Совокупность значений температур всех точек тела в
- 37. Градиент температуры. Интенсивность изменения температуры T характеризуется
- 38. Основной закон теплопроводности (Закон Фурье): Основной закон
- 39. Основной закон теплоотдачи (Ньютона-Рихмана) ,
- 40. V – в м/с Например, при
- 41. Коэффициент теплопроводности λ равен количеству тепла,
- 42. Дж/(кг*К) Теплоёмкость тела - отношение бесконечно малого количества теплоты
- 43. Теплоемкости различных металлов (Fe, Co, Cu, Ni) в зависимости от температуры.
- 45. Теплофизические характеристики песчаной формовочной смеси и некоторых литейных сплавов
- 46. Удельная теплота плавления металлов Удельная теплота плавления
- 47. 1.4. Уравнение теплопроводности Количество тепла, поступившего
- 48. Изменение энтальпии (теплосодержания) равно: При передаче тепла
- 49. Т.о. уравнение теплопроводности для одномерного нестационарного температурного
- 50. 1.5. Начальные и граничные условия Для
- 51. Граничные условия второго рода задают в виде
- 52. Температура стержня от мгновенного точечного источника тепла
- 53. При бесконечном удалении от вспыхнувшего источника
- 54. Для трехмерного нестационарного температурного поля
- 55. 1.7. Температурное поле в неограниченном теле
- 56. записанное в виде интеграла выражение
- 57. Поскольку функция θ(x, τ) удовлетворяет уравнению
- 58. По аналогии для плоской задачи : а для пространственной задачи :
- 59. 1.8. Температура полуограниченного стержня при постоянной температуре
- 60. Найти решение уравнения при краевых
- 61. Для этого продолжим стержень в область отрицательных
- 62. решение для температуры полуограниченного стержня с
- 63. 1.9. Температура полуограниченного стержня при постоянной температуре
- 64. Поскольку подынтегральная функция - четная, то в
- 65. Распределения температуры по длине стержня при различных значениях времени нагрева τ при
- 66. Плотность теплового потока на торце стержня на
- 67. Количество тепла Q , поступившего через торец стержня
- 68. 1.11. Температурное поле в полуограниченном или в
- 69. Математическая формулировка задачи: найти решение уравнения
- 70. Изменим порядок дифференцирования Перейдем к
- 71. запишем С учетом
- 72. Интегрируя , найдем решение для температуры полуограниченного
- 73. Для неограниченного стержня плотность теплового потока следует
- 74. еще один способ решения этой задачи
- 75. 1.12. Температурное поле в полуограниченном или в
- 76. Изменение температуры в интервале нагрева (0
- 77. Л. №4. 1.13. Численный
- 78. . . . .
- 79. Приращение безразмерной (гомологической) температуры в конце первого
- 80. 1.14. Свободное охлаждение равномерно нагретого тела,
- 81. При постоянной по всему объему температуре и
- 82. 1.15. Температурное поле двух соприкасающихся полуограниченных стержней
- 83. необходимо найти решение системы уравнений При краевых условиях:
- 84. Решение этой задачи имеет вид
- 85. 2. ДВИЖУЩИЕСЯ И НЕПОДВИЖНЫЕ НЕПРЕРЫВНО ДЕЙСТВУЮЩИЕ ТОЧЕЧНЫЕ
- 86. Результатом действия элементарного точечного источника
- 87. Неограниченное теплопроводящее тело находится при нулевой начальной
- 88. Принимая во внимание, что
- 89. 2.3. Непрерывно действующий
- 90. Элемент тепла от точечного источника
- 91. В подвижной системе координат X, Y, Z,
- 92. Интеграл (1) в пределах от 0 до
- 93. 2.5. Предельное состояние нагрева полубесконечного тела неподвижным
- 94. Ток короткого замыкания I= 250 А,
- 95. 2.6. Влияние скорости источника на распределение
- 96. Влияние скорости перемещения точечного источника на распределение
- 97. Распределение температуры от движущегося источника в
- 98. 2.7. Непрерывно действующий точечный источник тепла постоянной
- 99. Множитель учитывает теплоотдачу поверхн. в окружающую среду
- 100. С учетом выражения интеграла через бесселеву
- 101. Распределение температуры в стальной пластине δ= 3 мм 1,2 кВт
- 102. Распределение температуры в алюминиевой пластине δ= 3
- 103. Значения функции K(u) могут быть определены по
- 104. В пластине тепловой поток больше стеснен,
- 105. 2.8. Метод быстродвижущихся источников тепла Н.Н.Рыкалиным было
- 106. На каждой изотерме температурного поля быстродвижущегося источника
- 107. Температура от непрерывно действующего источника тепла, движущегося
- 108. Приращение количества тепла от точечного источника:
- 109. 2.9. Температурное поле в полуплоскости от движущегося
- 110. температура торца стержня Нестационарное температурное поле стержня
- 111. Схема к расчету температуры на укороченной передней
- 112. при определении приращения температуры в полуплоскости мощность
- 113. 2.10. Оценка погрешностей и области применения метода
- 114. Сопоставление изотерм температурного поля в с учетом масштабных коэффициентов
- 115. Воспользовавшись формулой вычислим угол ϕБ
- 116. Зависимость погрешности вычисления градиента температурного поля методом
- 117. При
- 118. При Z>1,45 тепловые потоки и
- 119. 2.11. Одномерное температурное поле от движущегося
- 120. при τ → ∞ и, соответственно, при
- 121. 3.1. Закономерности кристаллизации и затвердевания отливки в
- 122. Изменение плотности теплового потока и
- 123. 3.2. Закономерности отвода теплоты в литейную форму
- 124. Для первого интервала примем температуру на торце
- 126. Рис. Зависимость средней температуры расплава (отливки)
- 127. Закономерности отвода теплоты от заливки
- 128. а) Закономерности отвода теплоты
- 129. Охлаждение отливок в литейных формах после заливки
- 130. 3.3. Влияние теплофизических характеристик материалов песчаных и
- 131. Закономерности остывания стальной (а) и алюминиевой (б)
- 132. Теплофизические характеристики песчаной формовочной смеси и некоторых
- 133. Для регулирования теплообмена в литейную форму встраивают
- 134. Температуропроводность стальной формы в 40 раз больше,
- 135. литье алюминиевого кубика размерами 100 мм*100 мм*100 мм
- 136. 3.4. Теплообмен при литье под давлением
- 137. отливки из алюминиевого сплава размерами 10
- 138. 3.5. Теплообмен и температура при горячей прокатке
- 139. Время τ нагрева «стержня» В
- 140. Количество тепла Q1, поступившее в валки при
- 141. Температуру за пределами участка вычислим путем наложения
- 142. Еще через оборот валка остаточная поверхностная температура,
- 143. При непрерывной прокатке заготовки контактная температура увеличивается.
- 144. При полном выравнивании этой теплоты по всей
- 145. 3.6. Нагрев и охлаждение штампов при горячей
- 146. Распределение температуры в глубине штампа
- 147. Плотность теплового потока При
- 148. 3.7. Анализ теплового баланса при ручной
- 149. сварочные токи до 200 А, мощности
- 150. Примерный тепловой баланс при ручной дуговой сварке (по Н.Н.Рыкалину)
- 151. Пусть длина шва Lш , шов разделан
- 152. 2.Тепловой поток, поступающий в сварочный электрод Электрод
- 153. Т.к. Израсходованная длина
- 154. Баланс тепловых потоков при ручной
- 155. Схема автоматической дуговой сварки сварочные токи
- 156. Баланс тепловых потоков при автоматической
- 157. Схема сварки в защитных газах неплавящимся электродом
- 158. Баланс тепловых потоков при сварке алюминиевых
- 159. Схемы получения плазменной струи, выделенной из дуги
- 160. Баланс тепловых потоков при плазменной сварке стальная
- 161. Схема электрошлаковой сварки 1-трубы ползуна, 2
- 162. Баланс тепловых потоков при электрошлаковой сварке Стальная
- 163. 3.9. Температура при электрической контактной стыковой сварке
- 164. Температура в плоскости контакта (т.е. при
- 165. Зависимости тока I и усилия Р от
- 166. 3.10. Температура и количество теплоты при
- 167. Зависимости температуры от времени разряда при конденсаторной
- 168. Температура стыка свариваемых заготовок рассчитывается по формулам
- 169. при уменьшении времени действия источника тепла от
- 170. 3.11. Температура при сварке трением . Принципиальные
- 171. Плотность теплового потока (или удельная мощность
- 172. Зависимости температуры от времени нагрева при диаметрах
- 173. Решение может быть применено,
- 174. Зависимости температуры от расстояния от источника тепла
- 175. Стремление температуры от точечного источника к предельным
- 176. Зависимости температуры от расстояния от источника тепла
- 177. 3.13. Температура при электрической контактной шовной
- 178. Температура в окрестности движущегося точечного источника может
- 179. Распределение температуры в стальной пластине δ= 3 мм при шовной сварке N=1,2 кВт
- 180. Распределение температуры в алюминиевой пластине δ= 3 мм при шовной сварке N=1 кВт
- 181. 3. 14. Температура при ультразвуковой сварке
- 182. Установившееся распределение температуры в стальной
- 183. Источники теплоты: 1. зона стружкообразования,
- 184. Распределения температуры и тепловые потоки рассматривают в плоскости стружкообразования
- 185. Для расчета температуры деформации необходимо оценить мощность
- 186. 4.2. Анализ тепловых потоков, поступающих в стружку
- 187. Время нагрева стержня , выделенного в стружке,
- 188. Теплофизические характеристики обрабатываемого и инструментального материалов оказывают
- 189. . Схема к определению теплообмена между
- 190. 4.3. Тепловые потоки в инструмент и в
- 191. Схема к определению максимального угла контакта
- 192. 4.4. Тепловой поток от условной плоскости сдвига
- 193. Примет вид: где
- 194. Тепловой поток в
- 195. 4.6. Калориметрический метод измерения тепловых потоков, поступающих
- 196. Схема резания лопаточным резцом с обратными срезами
- 197. По истечении некоторого времени Δτ температуры ядра
- 198. Теплосодержание Q детали (втулки) определяется по формуле:
- 199. Для оценки теплоотдачи калориметра в окружающую среду
- 200. Средняя температура главного периода измерения
- 201. 4.7. Результаты измерения тепловых потоков, поступающих в
- 202. Экспериментальные результаты (рис.) подтверждают предположения о том,
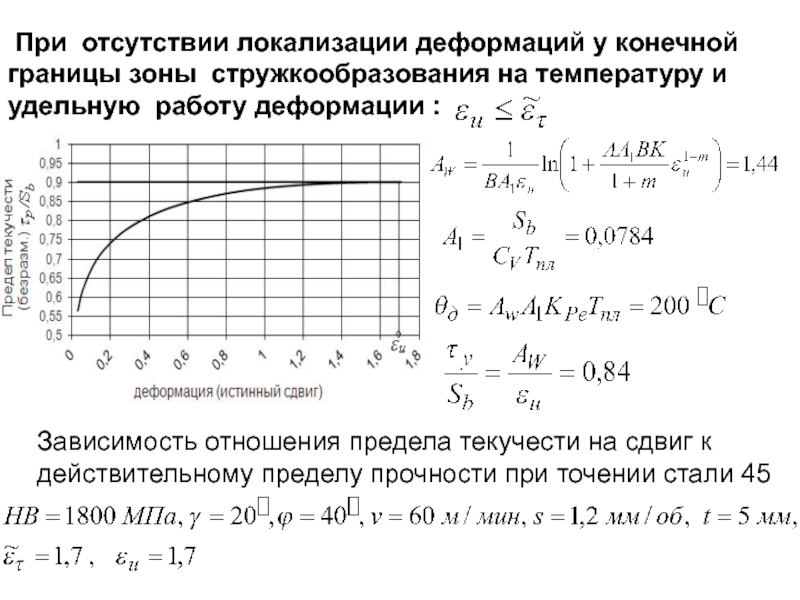
- 203. Опыты по определению тепловых потоков от застойной
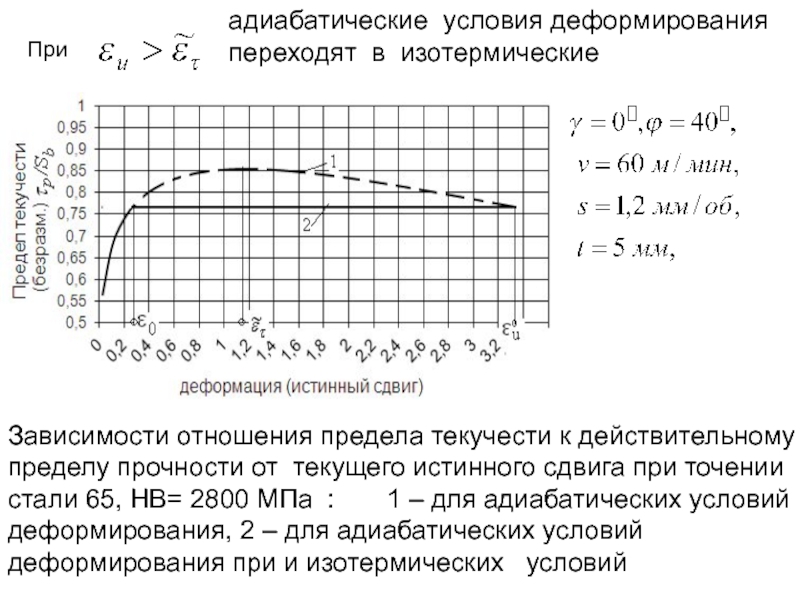
- 204. Опыты по определению тепловых потоков от фаски
- 205. Плотности тепловых потоков qФ вычислялись графическим дифференцированием
- 206. Зависимости плотности теплового потока q от
- 207. 4.8. Температура быстродвижущейся полуплоскости от равномерно
- 208. расчет температуры на участке пластического контакта стружки
- 209. температурное поле в полуплоскости описывается решением
- 210. Температуру торца стержня определим по формуле
- 211. Наибольшая температура будет иметь место при y=f
- 212. . Распределение температуры по укороченной передней поверхности
- 213. 4.9. Температура на границе быстродвижущейся полуплоскости от
- 214. Формулу (…..) преобразуем к виду: Участок
- 215. Схема замены линейно убывающего источника теплоты равномерно
- 216. значения гомологических температур :
- 217. Таблица к расчету температуры на участке упругого
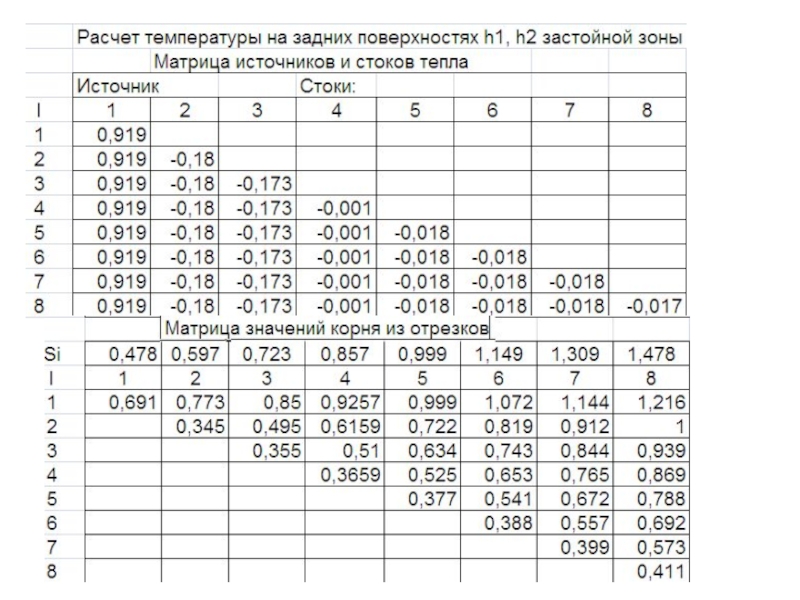
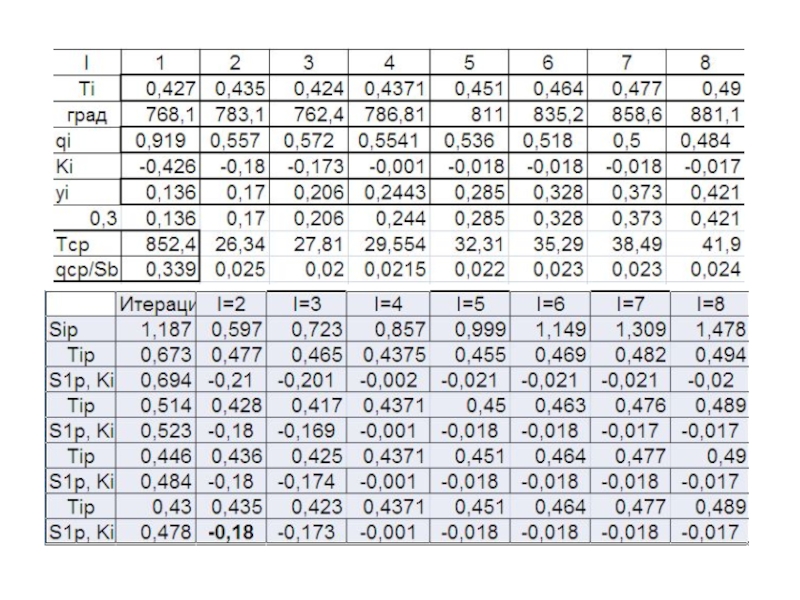
- 218. 4.10. Температура задней поверхности от равномерно распределенных
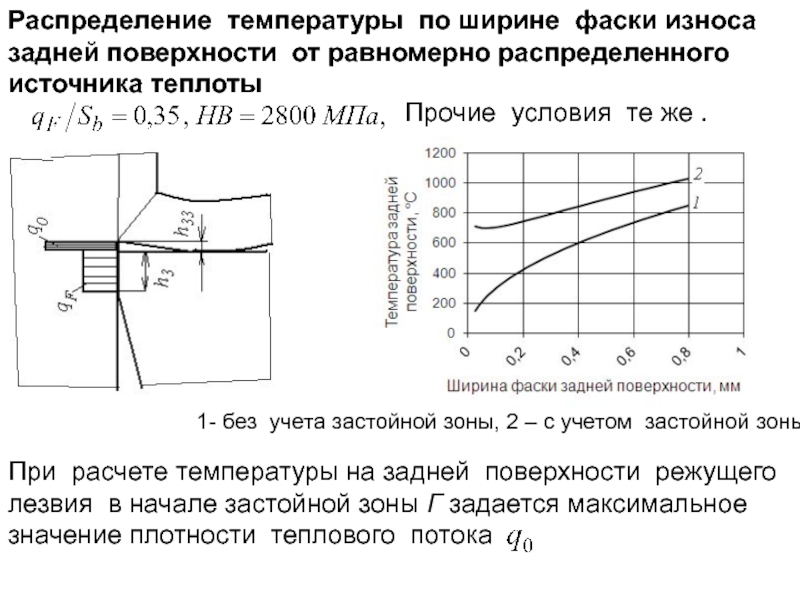
- 219. Температура на участке застойной зоны рассчитана
- 220. температуру на фаске износа определим суммируя приращения
- 221. Зависимость температуры задней поверхности от ширины фаски
- 222. 5. СОВЕРШЕНСТВОВАНИЕ РАСЧЕТА ТЕМПЕРАТУРЫ ПРИ РЕЗАНИИ НА
- 223. На основании данных Н.Н.Зорева [ ] о силах резания и усадке стружки
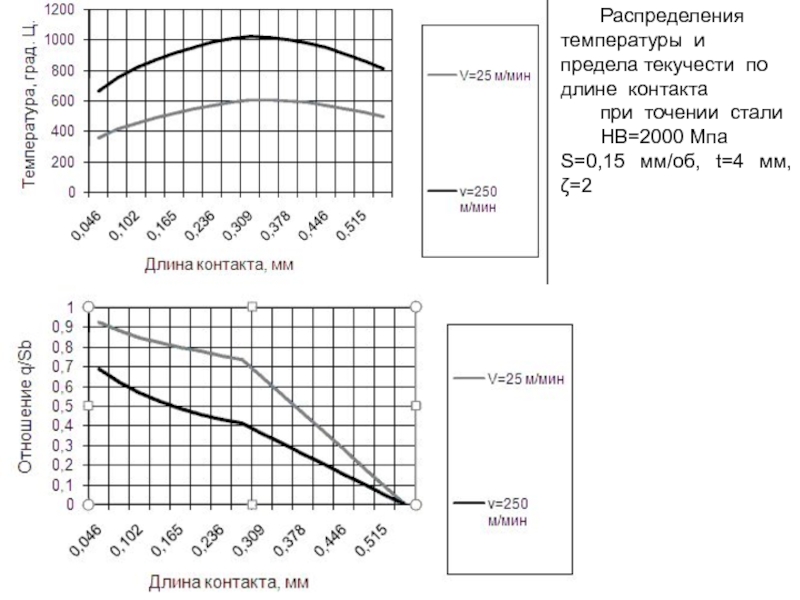
- 224. Распределение расчетной температуры по укороченной передней поверхности
- 225. Распределение отношения предела текучести на сдвиг к
- 226. Расчетные распределения температуры и плотностей тепловых потоков
- 227. 5.2. Сопротивление материалов большим пластическим деформациям в
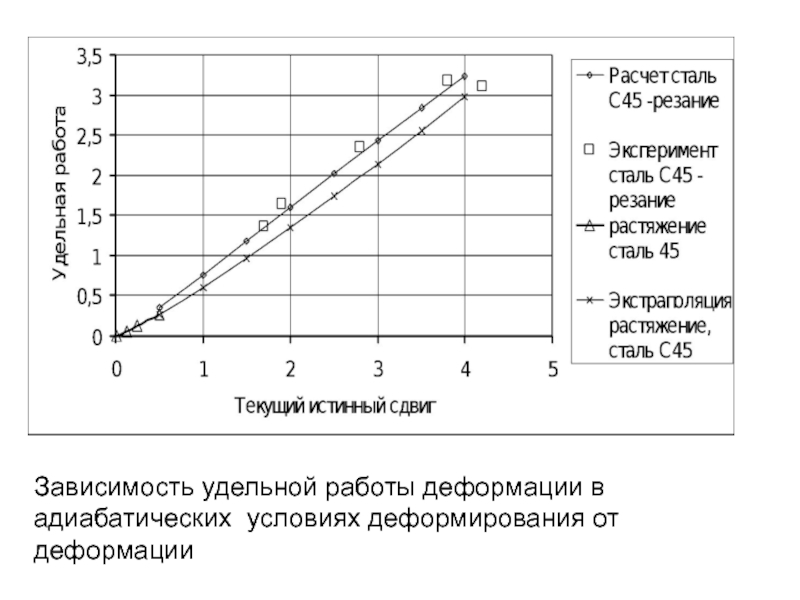
- 228. Зависимость удельной работы деформации в адиабатических условиях деформирования от деформации
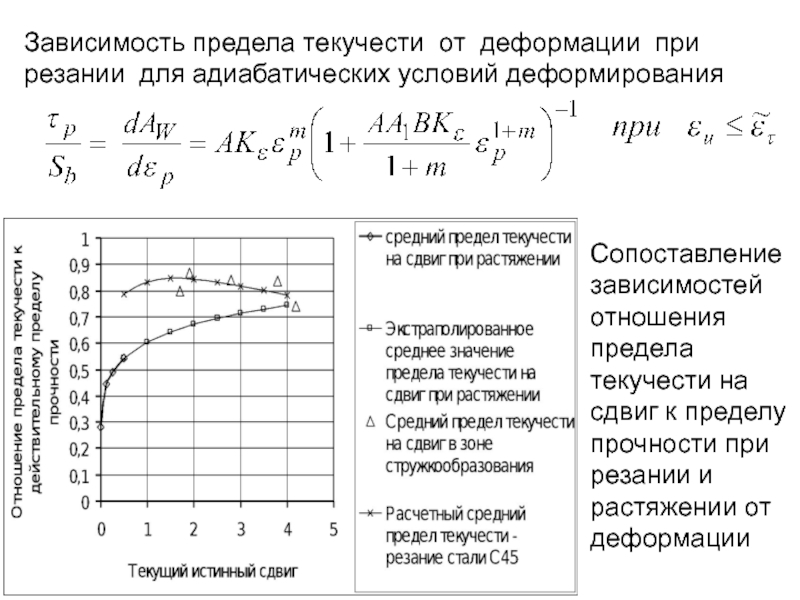
- 229. Зависимость предела текучести от деформации при резании
- 230. зависимость предела текучести на сдвиг от деформации
- 231. 5.3. Влияние локализации деформаций у конечной границы
- 232. температура деформации:
- 233. При этом дальнейшее увеличение деформации может происходить
- 234. При достижении условий локализации деформаций зависимость предела текучести от текущего истинного сдвига имеет вид:
- 235. Влияние локализации деформаций в узкой зоне на
- 236. Деформацию вычислим, аппроксимируя кривую течения параболой
- 237. 5. СОВЕРШЕНСТВОВАНИЕ РАСЧЕТА ТЕМПЕРАТУРЫ ПРИ РЕЗАНИИ НА
- 238. Удельные касательные силы в зоне стружкообразования и
- 239. На основании данных Н.Н.Зорева [ ] о силах резания и усадке стружки
- 240. , γ=10°, ϕ=70°, s=1,2 мм/об, t=
- 241. Схема к заданию плотностей тепловых потоков на
- 242. Результаты расчета температуры существенно завышены, так
- 243. Расчетные распределения температуры и плотностей тепловых потоков
- 244. . Резание стали с наростом на режущем лезвии при невысоких температурах [ ]
- 245. 5.2. Сопротивление материалов большим пластическим деформациям в
- 246. Зависимость удельной работы деформации в адиабатических условиях деформирования от деформации
- 247. Зависимость предела текучести от деформации при резании
- 248. зависимость предела текучести на сдвиг от деформации
- 249. При отсутствии локализации деформаций у конечной
- 250. При адиабатические условия деформирования
- 251. Влияние локализации деформаций в узкой зоне на
- 252. безразмерная удельная работа будет: температура
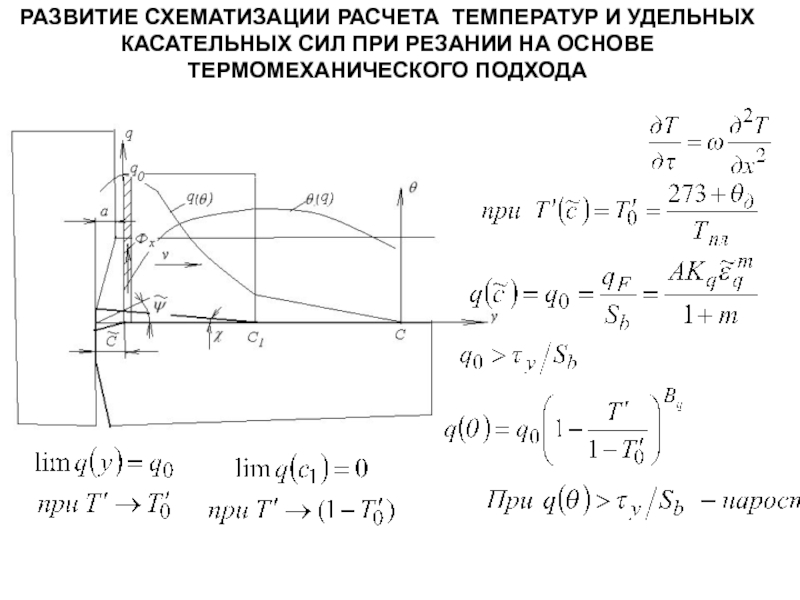
- 254. 5.4. Схематизация расчета температур на основе термомеханического
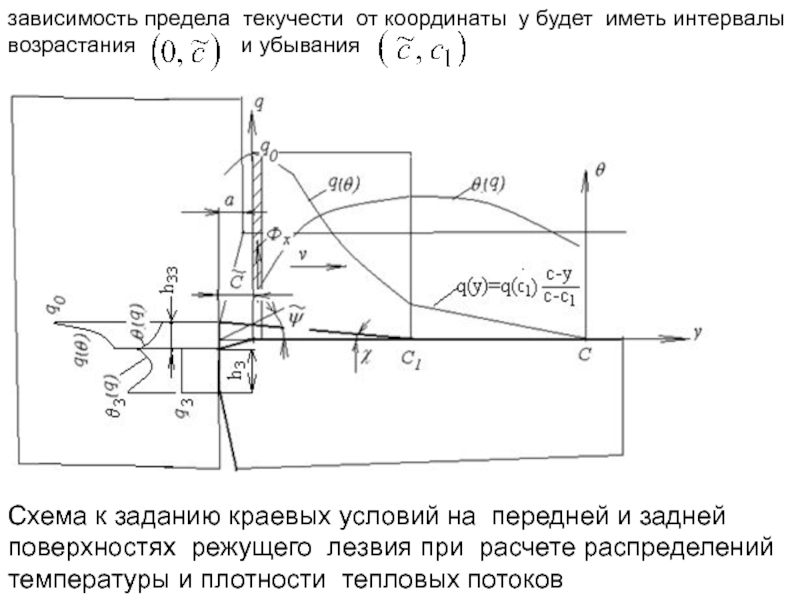
- 255. Схема к заданию краевых условий на передней
- 256. где Максимальное значение
- 257. В интервале разупрочнения для любой координаты
- 258. Распределение температуры по ширине фаски износа задней
- 259. РАЗВИТИЕ СХЕМАТИЗАЦИИ РАСЧЕТА ТЕМПЕРАТУР И УДЕЛЬНЫХ КАСАТЕЛЬНЫХ СИЛ ПРИ РЕЗАНИИ НА ОСНОВЕ ТЕРМОМЕХАНИЧЕСКОГО ПОДХОДА
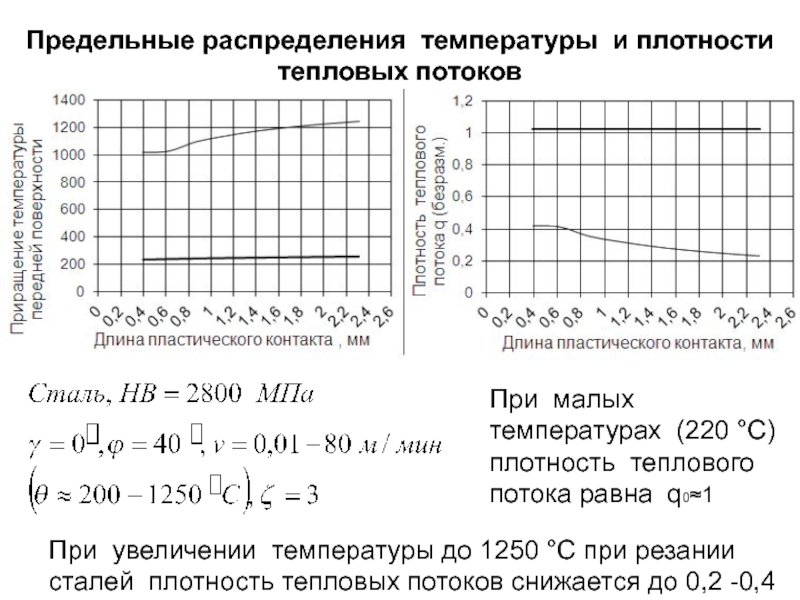
- 260. Предельные распределения температуры и плотности тепловых потоков
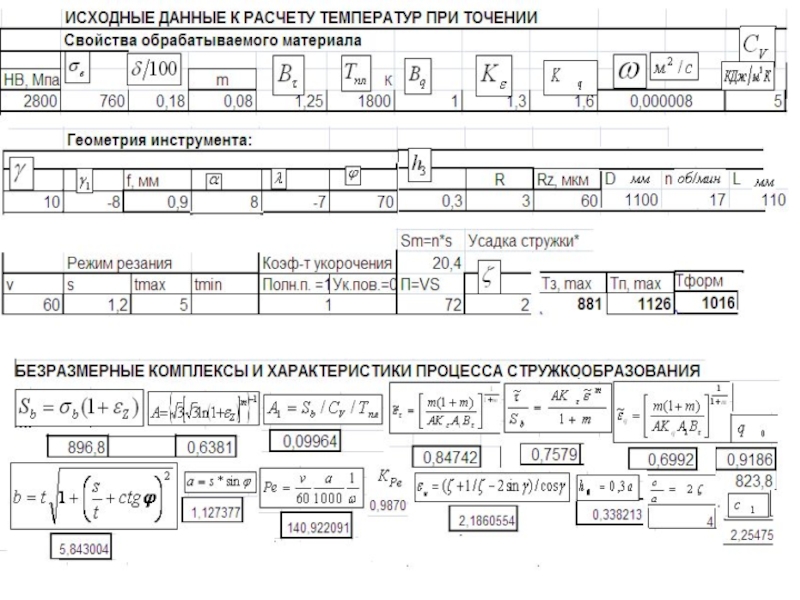
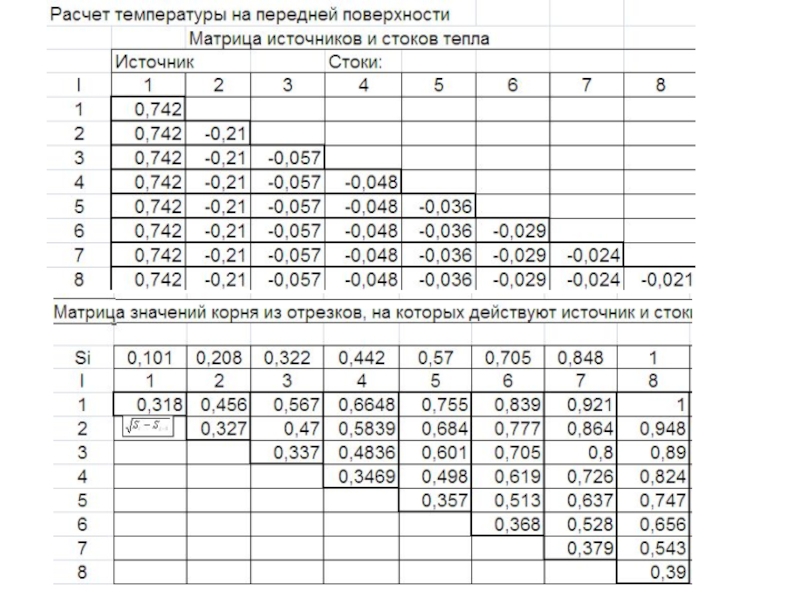
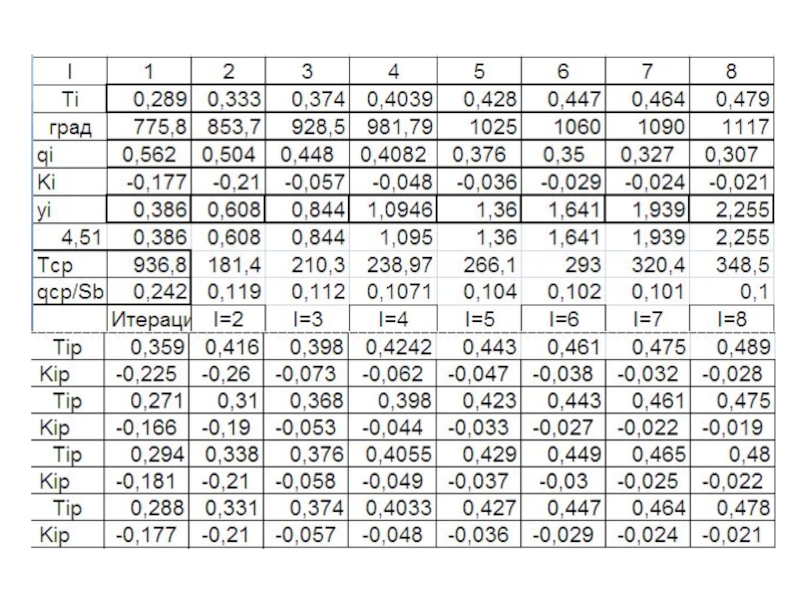
- 261. Схема итераций при расчете температуры и предела
- 263. 1,22815 0,6721
- 266. Распределения температуры и предела текучести по длине
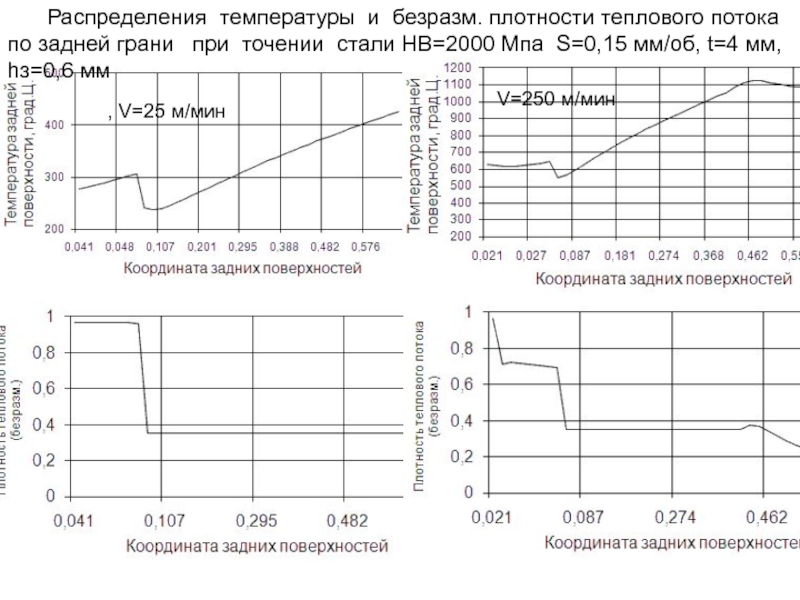
- 269. Распределения температуры и безразм. плотности теплового потока
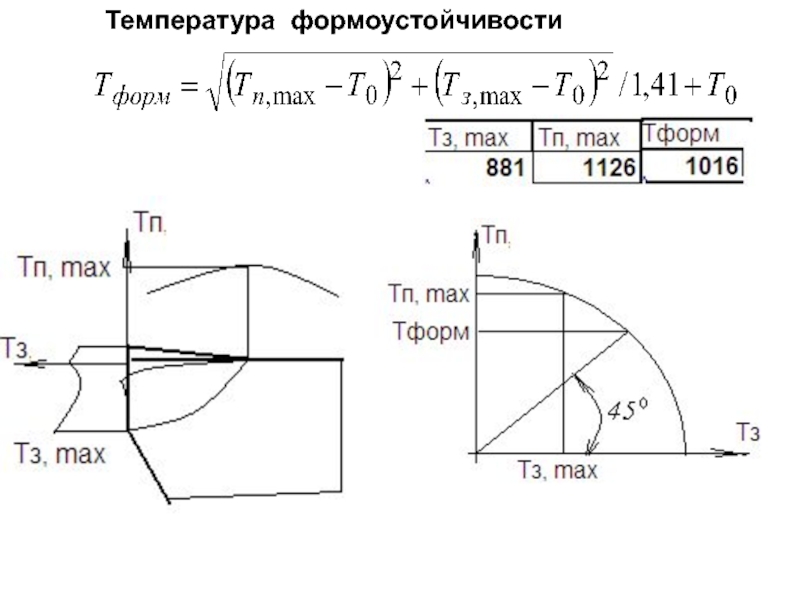
- 270. Температура формоустойчивости
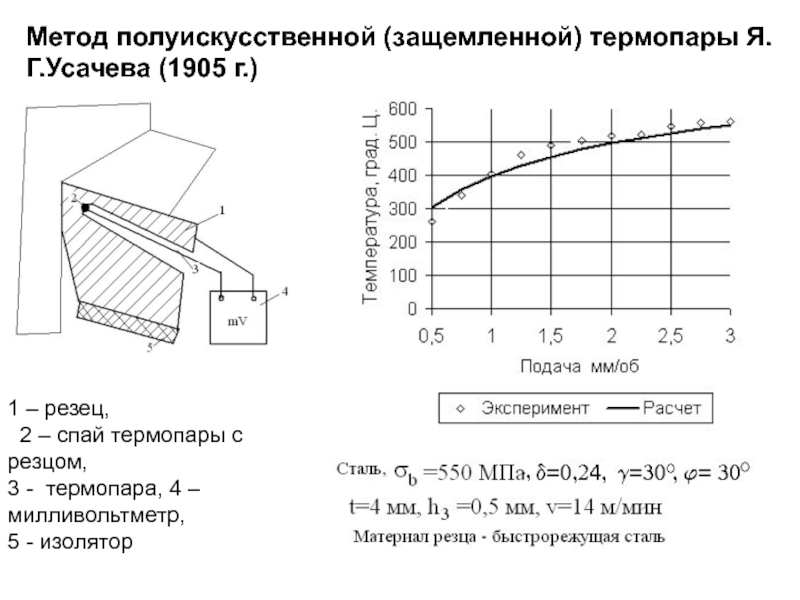
- 271. Метод полуискусственной (защемленной) термопары Я.Г.Усачева (1905 г.)
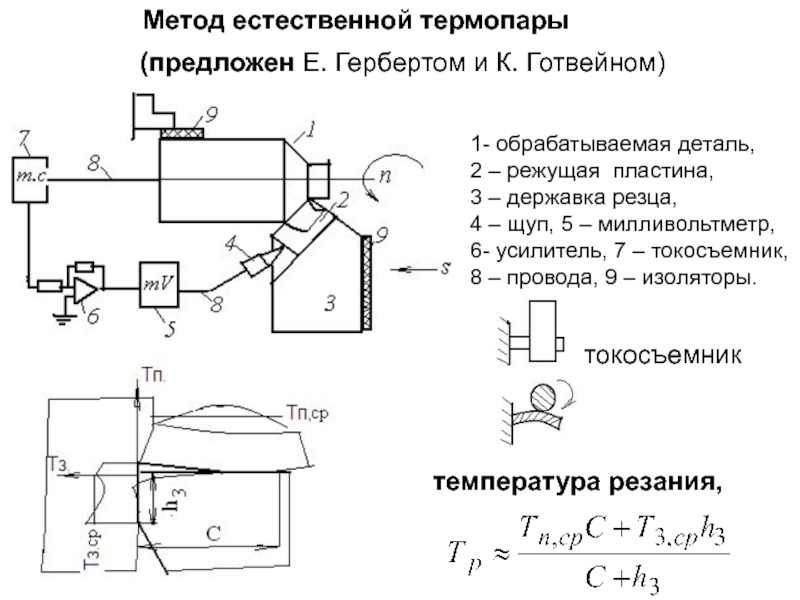
- 272. Метод естественной термопары 1- обрабатываемая деталь, 2
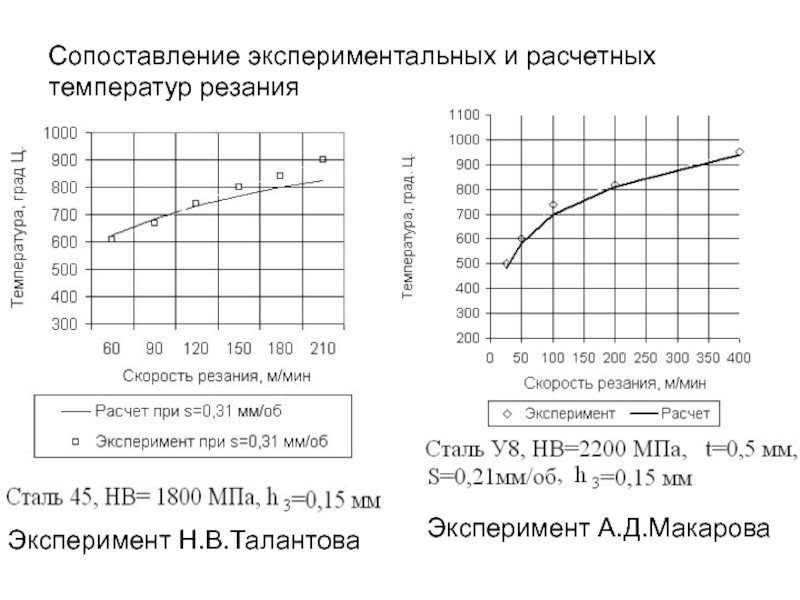
- 273. Сопоставление экспериментальных и расчетных температур резания Эксперимент Н.В.Талантова Эксперимент А.Д.Макарова
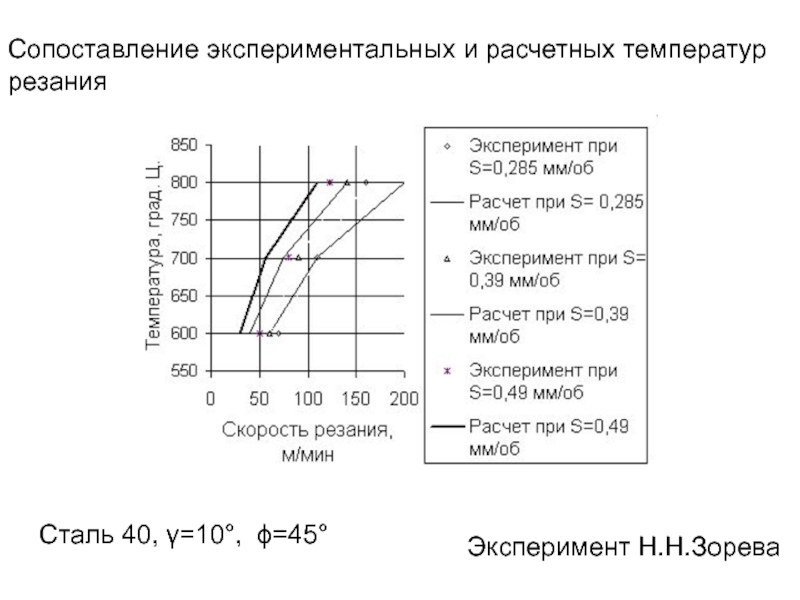
- 274. Сталь 40, γ=10°, ϕ=45° Эксперимент Н.Н.Зорева Сопоставление экспериментальных и расчетных температур резания
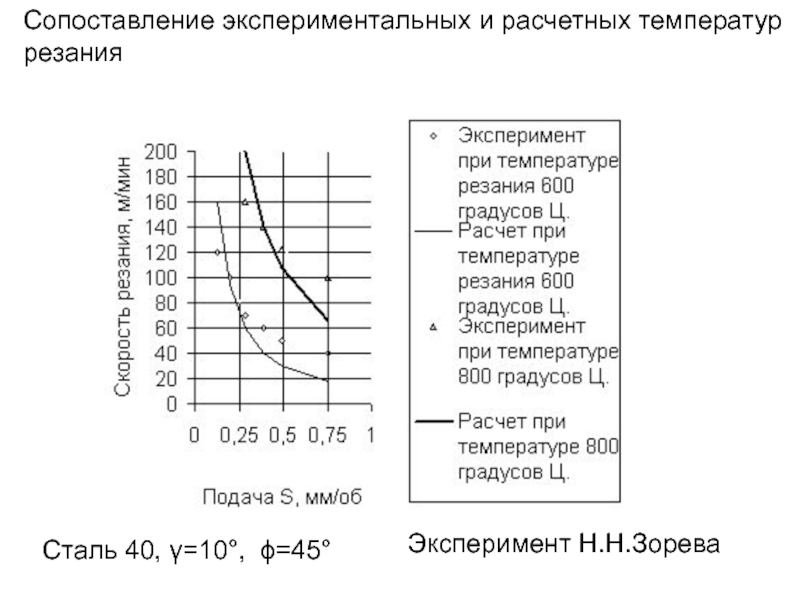
- 275. Сталь 40, γ=10°, ϕ=45° Эксперимент Н.Н.Зорева Сопоставление экспериментальных и расчетных температур резания
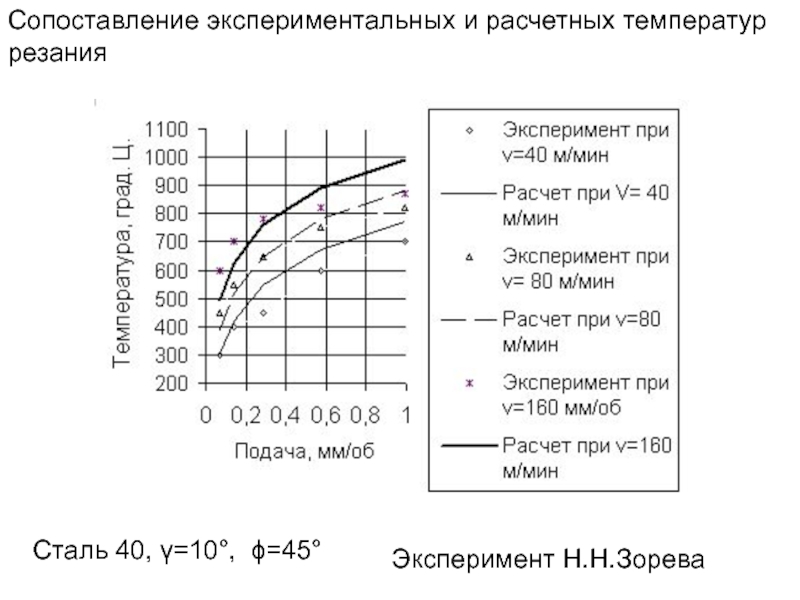
- 276. Сталь 40, γ=10°, ϕ=45° Эксперимент Н.Н.Зорева Сопоставление экспериментальных и расчетных температур резания
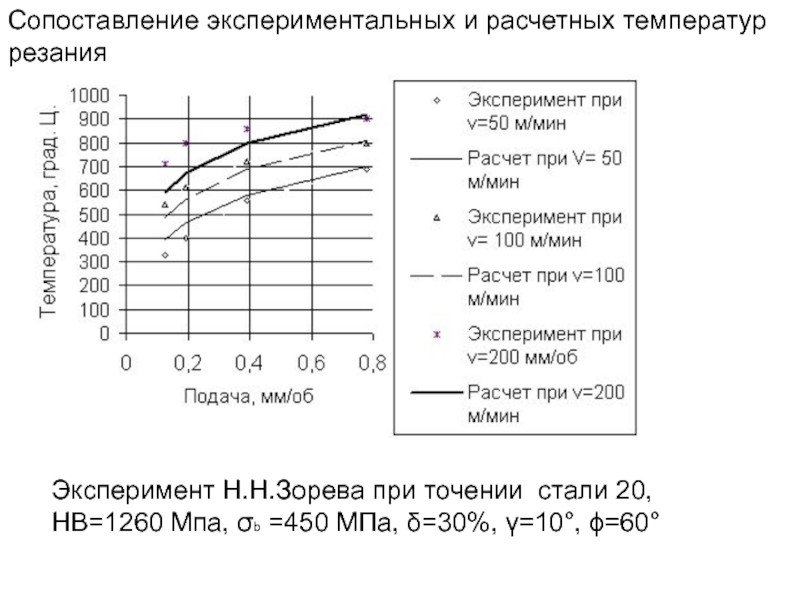
- 277. Эксперимент Н.Н.Зорева при точении стали 20, HB=1260
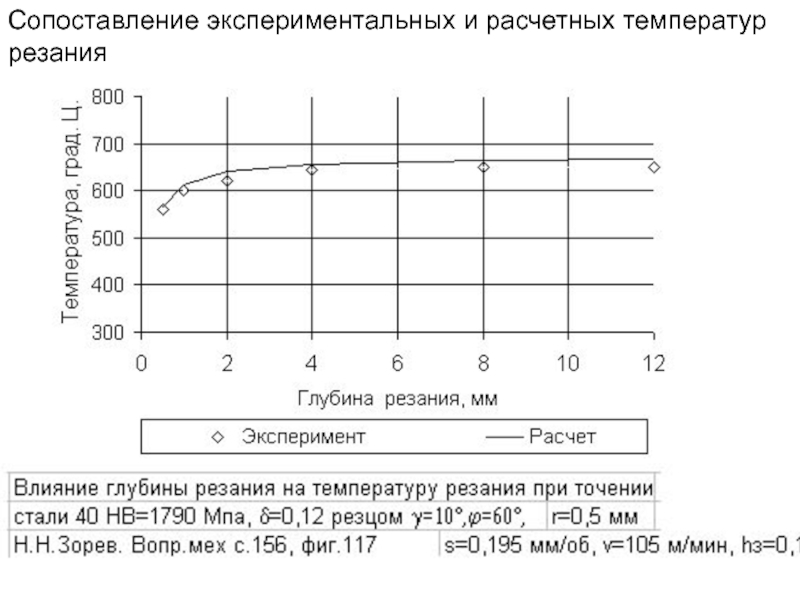
- 278. Сопоставление экспериментальных и расчетных температур резания
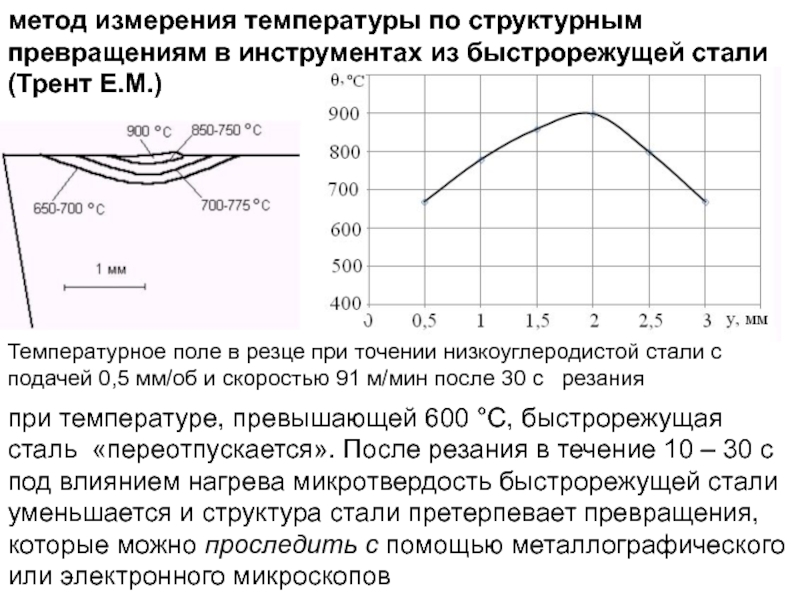
- 279. метод измерения температуры по структурным превращениям в
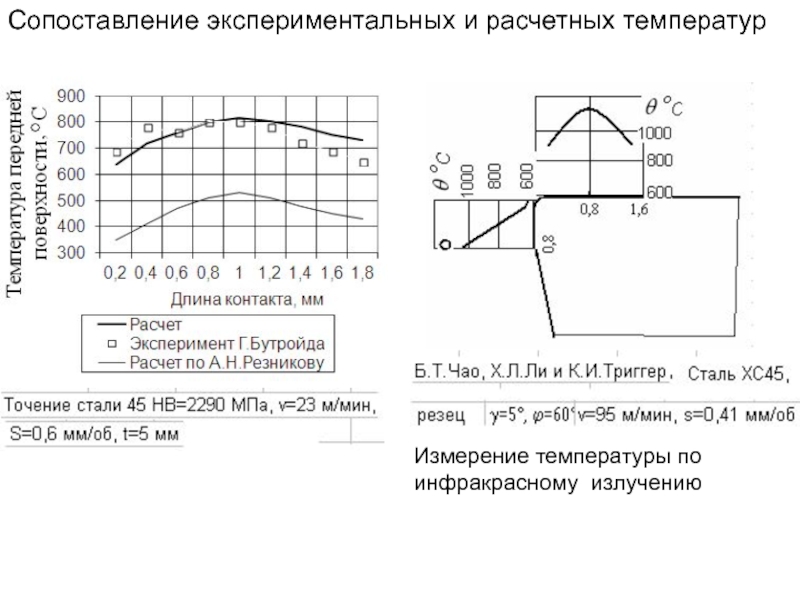
- 280. Измерение температуры по инфракрасному излучению Сопоставление экспериментальных и расчетных температур
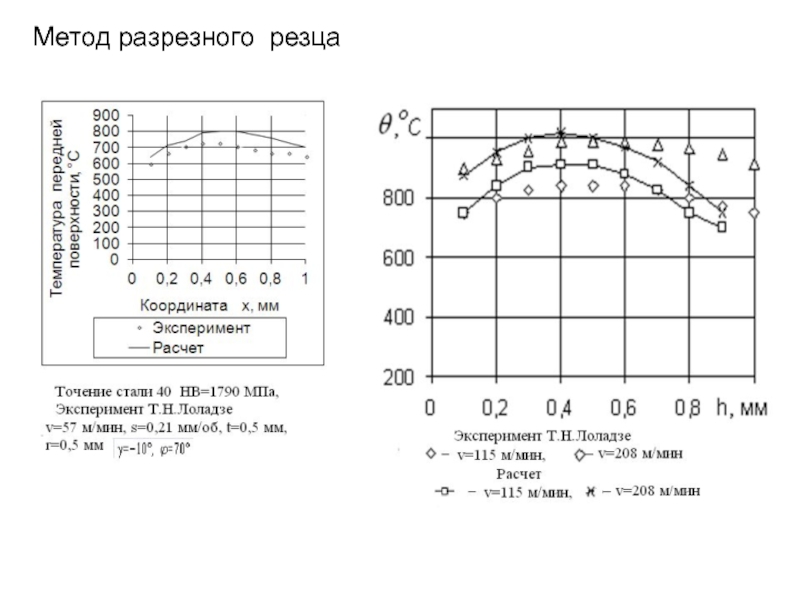
- 281. Метод разрезного резца
Слайд 1Литература:
1.Кушнер В.С. Технологические процессы в машиностроении: учебник для студ.высш.учеб.заведений/ В.С.Кушнер,
2. Кушнер В.С. Технологические процессы в машиностроении. Часть1:Металлургия, литейное производство и обработка резанием: Учеб для машиностроительных направлений и специальностей технических университетов /В.С.Кушнер, А.С.Верещака, А.Г.Схиртладзе, Д.А.Негров, -Омск, Изд-во ОмГТУ,2005.- 200 с.
3. Кушнер В.С. Технологические процессы в машиностроении. Часть2:Обработка давлением и сварочное производство Учеб для машиностроительных направлений и специальностей технических университетов /В.С.Кушнер, А.С.Верещака, А.Г.Схиртладзе, Д.А.Негров, -Омск, Изд-во ОмГТУ,2005.-200 с.
4. Кушнер В.С. Технологические процессы в машиностроении. Часть3: Тесты для контроля остаточных знаний и текущего контроля знаний: Учеб.для вузов /В.С.Кушнер, А.С.Верещака, А.Г.Схиртладзе, Д.А.Негров, -Омск, Изд-во ОмГТУ,2006.-172 с.
4. Способы обработки конструкционных материалов: -обработка резанием:Кушнер В.С. и др. Метод.указ.к лабор.работам- Омск, Изд-во ОмГТУ,2011
5. Способы обработки конструкционных материалов: -обработка литьем Кушнер В.С. и др. Метод.указ.к лабор.работам- Омск, Изд-во ОмГТУ, . Способы обработки конструкционных материалов: -обработка давлением Кушнер В.С. и др. Метод.указ.к лабор.работам- Омск, Изд-во ОмГТУ,
Слайд 2Лекция №1
Основными задачами дисциплины «Физические основы
технологических процессов» являются :
научиться
характеристики технологического оборудования при
применении металлургических и машиностроительных
технологий, основанных на изменении агрегатного
состояния материала , а также на формоизменении
заготовок и деталей путем механической обработки
назначать рациональные технологические режимы обработки
материалов и получения заготовок и деталей в различных
металлургических и машиностроительных производствах
научиться анализировать и моделировать механические,
тепловые и термомеханические физические явления ,
составляющие суть разнообразных технологических
процессов , на основе общих фундаментальных физических
законов
Введение
Слайд 3Физические процессы разнообразных металлургических и машиностроительных технологий в значительной мере основаны
Изучение физических основ технологических процессов
и способов производства и обработки важно для более
глубокого понимания изучаемых процессов и технологий.
По особенностям формообразования различают литейные технологии, основанные на изменении агрегатного состояния, технологии обработки материалов давлением , резанием , сварочные технологии и др.
Слайд 4Следуя традициям, заложенным в теоретической механике,
основными разделами механики считают кинематику (твердого
С позиций кинематики обычно классифицируют и схематизируют различные технологические процессы (способы).
Иллюстрацией этого является классификация и схематизация способов лезвийной обработки материалов резанием.
Слайд 5Влияние условий деформирования на сопротивление
материалов пластическим деформациям
Идеально пластическое тело
Повышение температуры
Абсолютная температура, при которой отдых и рекристаллизация происходят более интенсивно, чем искажение кристаллической решетки и упрочнение пропорциональна абсолютной температуре плавления
Для металлов обычной технической чистоты
Отношение абсолютной температуры к абсолютной температуре плавления называют гомологической температурой
Горячей называют деформацию при температуре, равной или выше температуры рекристаллизации. при горячей деформации при постоянной температуре и постоянной скорости деформации имеют вид прямой, параллельной оси деформации
Слайд 6
для свинца, имеющего температуру плавления Тпл=600 К при комнатной
температуре гомологическая температура равна:
для стали , имеющей температуру плавления 1800 К, идеальная пластичность может быть при температуре около 700 - 900 К
(400 - 600 град. Цельсия)
Схема к определению удельных касательных сил при резании
Слайд 8Простое нагружение, теория течения
Пластические деформации вызывают повышение плотности дислокаций, искажение кристаллической
Холодной называют деформацию при температуре ниже температуры
рекристаллизации.
Слайд 9
по Н.Н.Зореву
по М.Ф.Полетике и Н.Н.Зореву
Модель идеально-пластического тела или
теория течения
Слайд 10
Влияние температуры на предел прочности стали 45
Влияние температуры деформации при растяжении
Слайд 11
. Влияние температуры на средний предел текучести при точении сталей: при
Влияние температуры при резании
Слайд 12
Влияние скорости деформации при растяжении
Влияние скорости деформации и температуры на
при относительном удлинении δ = 20 %
Коэффициент динамичности
Слайд 13
резание сталей 00, 10, 20Х, Х18Н9Т
Со скоростью резания v = 0,2 м/мин a = 0,22 мм
Влияние скорости деформации при резании
обобщенное определяющее уравнение :
Слайд 14Сопротивление материалов большим пластическим деформациям в адиабатических условиях деформирования
Слайд 15
Удельная работа деформации
Гипотеза о равенстве удельных работ при сжатии и резании
А.М.Розенберга
Слайд 16Влияние локализации деформаций в узкой зоне на зависимости удельной работы от
Слайд 17
Кривая течения для адиабатических условия деформирования
Гипотеза о единой кривой
Слайд 18Действительные характеристики сопротивления материала
пластическим деформациям в адиабатических условиях
условие локализации
Слайд 20СИЛЫ РЕЗАНИЯ
Схема технологических осей x, y, z и физических составляющих
Слайд 23Теоретическое определение усадки при постоянных касательных напряжениях
Точение стали 65Г:
1-v=0,4 м/с,
3-v=0,8 м/с, 4-v=1,25 м/с,
5 – теория по формуле (1)
(1)
Слайд 25Влияние ширины фаски износа
на силы Pxy и Pz
Сталь 40ХНМА,
Удельные силы на задней поверхности
Слайд 27Напряжения в клине под действием сосредоточенной силы, действующей на острие клина
касательные напряжения на поверхности режущего клина
Радиальные (сжимающие) напряжения
Слайд 29В системе координат ξ1,ν1, повернутой на угол (γ+β/2) относительно координат ξ,ν,
Слайд 30Силы на задней поверхности в координатах ξ,ν:
в новых координатах ξ1,ν1
для тангенциальной
Слайд 31
Наибольшие касательные напряжения на поверхности клина
при
, учитывая, что
где
Радиальные (сжимающие) напряжения
Слайд 32
радиальное напряжение
при θ=π/2,
Т.о. уменьшение угла заострения β (увеличение γ)
касательные и особенно нормальные напряжения. С увеличением
ρ нормальные напряжения уменьшаются.
Слайд 33Наиболее благоприятными значениями ширины фаски износа
и толщины среза следует считать такие,
минимальные или допускаемые
касательные напряжения.
Т.о. критерий затупления -
ширину фаски износа h*
следует назначать с учетом
уровня касательных напряжений
Слайд 35ТЕПЛОФИЗИКА ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
три основных вида теплообмена: теплопроводность, конвекция и
Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).
Конвекция осуществляется путем перемещения в пространстве неравномерно нагретых объемов среды. При этом перенос теплоты неразрывно связан с переносом самой среды.
Тепловое излучение характеризуется переносом энергии от одного тела к другому электромагнитными волнами.
Передача теплоты теплопроводностью связана с наличием разности температур тела.
1.1.Виды теплообмена. Температурное поле. Градиент температуры.
Л.3.
Слайд 36Совокупность значений температур всех точек тела в данный момент времени называется
Если температура тела не изменяется с течением времени, то температурное поле называется стационарным.
- нестационарное объемное температурное поле
Температурное поле может быть также плоским или одномерным
Точки тела с одинаковой температурой образуют изотермическую поверхность (для объемного температурного поля) или изотермическую линию (изотерму) (для двухмерного температурного поля .
Слайд 37Градиент температуры.
Интенсивность изменения температуры T характеризуется производной по направлению s, принимающей
Вектор, направленный по нормали к изотермической поверхности в сторону
возрастания температуры, модуль которого равен производной температуры
по этому направлению, называется градиентом температурного поля.
для одномерного температурного поля T(x,τ)
Для двухмерного нестационарного температурного поля
а для трехмерного поля:
Слайд 38Основной закон теплопроводности (Закон Фурье):
Основной закон теплопроводности, коэффициент теплопроводности
плотность теплового потока
температуры
Количество тепла, поступившее через изотермическую поверхность площадью F за единицу времени, называют тепловым потоком Ф:
Тепловой поток, отнесенный к единице площади изотермической поверхности, называют плотностью теплового потока
1.2. Основные законы теплопроводности (Фурье) и теплоотдачи.(Ньютона – Рихмана)
Слайд 39Основной закон теплоотдачи (Ньютона-Рихмана) , коэффициент теплоотдачи
Основной
Q = α · (Тп - Тс )·F ,
или
q = α · (Тп - Тс ) ,
где: коэффициент теплоотдачи α [Вт/(м2К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.
Слайд 40V – в м/с
Например, при
Влияние охлаждения путем теплоотдачи в воздух
Слайд 41Коэффициент теплопроводности λ равен количеству тепла,
протекающему за единицу времени через
при перепаде температуры на единицу длины, равном одному градусу.
1.3. Теплофизические характеристики материалов
коэффициент пропорциональности плотности теплового потока градиенту
температуры, называется коэффициентом теплопроводности.
Размерность коэффициента теплопроводности определяется отношением размерностей плотности теплового потока и градиента температуры:
ватт на метр-кельвин (Вт/(м К)).
Слайд 42Дж/(кг*К)
Теплоёмкость тела - отношение бесконечно малого количества теплоты
полученного телом, к соответствующему
Уде́льная теплоёмкость —
отношение теплоемкости
к массе
Объемная теплоемкость — это количество теплоты, которое необходимо подвести к единице объема вещества, чтобы нагреть его на единицу температуры.
Теплоёмкость
Единица измерения теплоёмкости в —Дж/К.
Слайд 46Удельная теплота плавления металлов
Удельная теплота плавления количество теплоты , которое необходимо сообщить
Слайд 471.4. Уравнение теплопроводности
Количество тепла, поступившего за время Δτ
Здесь линейная часть приращения плотности теплового потока :
С учетом основного закона теплопроводности приращение количества тепла равно:
Слайд 48Изменение энтальпии (теплосодержания) равно:
При передаче тепла теплопроводностью количество тепла, поступившее в
Приравнивая , получим:
Слайд 49Т.о. уравнение теплопроводности для одномерного нестационарного температурного поля
Уравнение теплопроводности для
Уравнение теплопроводности для трехмерного нестационарного температурного поля
Коэффициент температу-
ропроводности
Слайд 501.5. Начальные и граничные условия
Для получения частного решения дифференциального уравнения
теплопроводности задают начальные и граничные условия.
Начальное условие задает распределение температуры внутри тела
(для одномерного поля - в стержне) в начальный момент времени:
где f(x) - известная функция.
Важным частным случаем является равномерное распределение температуры
в начальный момент времени:
Граничные условия задают различными способами:
Граничные условия первого рода задают в виде распределения температуры
на поверхности тела (на торце стержня) в любой момент времени :
Важным частным случаем является задание постоянной температуры:
Слайд 51Граничные условия второго рода задают в виде распределения плотности
теплового потока
и, в частности, - постоянную во времени плотность теплового потока :
граничные условия третьего рода характеризуют конвективный теплообмен между поверхностью тела и движущейся окружающей средой при постоянном потоке тепла
Плотность теплового потока qn, уносящегося средой, считают пропорциональной разности температур поверхности тела и среды:
qn =α(Tп - T с ), где α - коэффициент теплообмена, Вт/(м2К):
При этом условия теплообмена на поверхности:
граничные условия четвертого рода для двух твердых тел в контакте
Слайд 52Температура стержня от мгновенного точечного источника тепла
Распределения температуры
вдоль стержня
=5 К/м, ω=0,000008
1.6. Температура от точечного мгновенного источника тепла для трехмерного, двухмерного и одномерного нестационарных полей
Слайд 53
При бесконечном удалении от вспыхнувшего источника
теплоты приращение температуры стремится к
2. функция G(x,ξ ,τ) имеет максимум в точке x=ξ,
3. количество тепла Q в любой момент времени остается неизменным
Свойства функции точечного источника:
4. Величина
представляет собой площадь,
ограниченную функцией θ(x,τ) и осью x.
5. Функция G(x, ξ, τ) интерпретируется как частное решение для распределения температуры в неограниченном однородном и изотропном стержне от мгновенного точечного источника теплоты
Слайд 54
Для трехмерного нестационарного температурного поля
температура от точечного источника, вспыхнувшего
в
Температурное поле от точечного источника на плоскости
описывается функцией :
С учетом теплоотдачи граничных плоскостей:
где
Слайд 55 1.7. Температурное поле в неограниченном теле при граничных условиях первого
площадь под графиком распределения
температуры на элементарном участке dξ
равна отношению теплосодержания ΔQ
к удельной объемной теплоемкости
Приращение температуры dθ на этом интервале представим в виде:
а начальные условия, заданные известной функцией
в виде:
С помощью линейной суперпозиции решений для точечного источника можно сконструировать частное решение уравнения теплопроводности для граничных условий первого рода.
Слайд 56записанное в виде интеграла выражение
при τ→0 стремится к f(x).
Для
новой переменной u :
Слайд 57
Поскольку функция θ(x, τ) удовлетворяет уравнению
теплопроводности и начальным условиям,
в неограниченном стержне от заданного распределения
температуры в начальный момент времени.
Из этого следует, что функция
удовлетворяет начальному условию:
Слайд 591.8. Температура полуограниченного стержня при постоянной температуре торца стержня
Пусть в
а торец стержня имеет температуру , постоянную в течение всего периода теплообмена.
Рассмотрим задачу охлаждения стержня, поскольку задача нагревания может быть описана этим же решением с помощью замены переменной.
Для упрощения расчета примем .
Поставленная задача математически формулируется следующим образом:
Слайд 60Найти решение уравнения
при краевых условиях:
Решение этой задачи может быть получено как
Слайд 61Для этого продолжим стержень в область отрицательных значений x , т.е.
При этом при x=0 температуры
, т.е. граничное условие на поверхности выполняется
Слайд 62решение для температуры полуограниченного стержня
с нулевой температурой на торце примет
Слайд 631.9. Температура полуограниченного стержня при постоянной температуре торца стержня и постоянной
При постоянной начальной температуре полуограниченного стержня
Решение можно упростить, подставив в первую часть подынтегральной функции
а во вторую:
Слайд 64Поскольку подынтегральная функция - четная, то в силу симметрии
- функция ошибок
Практически
Если торец стержня поддерживается не при нулевой температуре, а при постоянной температуре , то решение получим с помощью замены переменной
Слайд 66Плотность теплового потока на торце стержня
на основании закона Фурье найдем плотность
Зависимость плотности теплового потока на торце стержня от времени поддержания на торце температуры 1000 °С при
Коэффициент
аккумуляции тепла,
Слайд 67Количество тепла Q , поступившего через торец стержня площадью F при его
Зависимость теплоты, отведенной в стержень поперечного сечения
при
и
1.10. Тепловой поток и количество теплоты поступившей в стержень при нагреве (или отведенное при охлаждении)
Слайд 681.11. Температурное поле в полуограниченном или в неограниченном стержне при граничных
эта задача (рис.) может быть сведена к задаче об одномерном нестационарном температурном поле при граничных условиях первого рода
Зависимость температуры в точке действия точечного источника (а), схемы действия точечного источника для полуограниченного стержня (б) и для неограниченного стержня (в)
Слайд 69Математическая формулировка задачи:
найти решение уравнения
удовлетворяющее краевым условиям:
Продифференцируем (1) по x:
(1)
Слайд 70Изменим порядок дифференцирования
Перейдем к новой переменной - плотности теплового потока:
Начальные
Воспользовавшись известным решением
Слайд 72Интегрируя , найдем решение для температуры полуограниченного стержня, на торце которого
Из (1) , в частности, следует, что на торце стержня, т.е. при x=0 температура описывается простой формулой
(1)
Слайд 73Для неограниченного стержня плотность теплового потока следует принять вдвое меньшей, поскольку
Слайд 74еще один способ решения этой задачи
В частности при x=ξ=0 получим формулу
Для полуограниченного стержня плотность теплового потока необходимо удвоить
Слайд 751.12. Температурное поле в полуограниченном или в неограниченном стержне после прекращения
Для расчета температуры после прекращения действия источника продлим источник тепла и добавим сток той же плотности теплового потока
Слайд 76Изменение температуры в интервале нагрева (0
Слайд 77Л. №4. 1.13. Численный метод расчета температуры неограниченного
Схема замены убывающей зависимости плотности теплового потока от времени суперпозицией источника и стоков
Слайд 79Приращение безразмерной (гомологической) температуры в конце первого интервала времени
На следующих интервалах,
. . . . . . . . . . . . . . . .
Слайд 801.14. Свободное охлаждение равномерно нагретого тела,
пластины, стержня (граничные условия третьего
Элементарный объем стержня Fdx, нагретый до температуры
T, отдает за время dτ через боковую поверхность pdx (где p-
периметр) в окружающую среду с нулевой температурой
количество тепла dQ = αTp dx dτ.
С учетом теплоотдачи уравнение теплового баланса
элементарного объема Fdx примет вид:
Или:
Соответственно, для пластины толщиной δ:
Слайд 81При постоянной по всему объему температуре
и уравнение теплопроводности примет вид:
Начальные
при τ= 0 T=T0
Следовательно:
или
Слайд 821.15. Температурное поле двух соприкасающихся полуограниченных стержней (граничные условия четвертого рода)
Два
в начальный момент времени приведены в соприкосновение, причем начало координат находится в месте соприкосновения
Слайд 84Решение этой задачи имеет вид
коэффициент тепловой активности .
При
и τ→∞
Т.е. на границе
Слайд 852. ДВИЖУЩИЕСЯ И НЕПОДВИЖНЫЕ НЕПРЕРЫВНО ДЕЙСТВУЮЩИЕ ТОЧЕЧНЫЕ ИСТОЧНИКИ ТЕПЛА
2.1. Схематизация
движущегося точечного источника
Для движущихся источников тепла координату источника задают в виде функции:
отрезок времени действия источника разбивают на элементарные интервалы
и считают, что в каждом из этих интервалов в точке с абсциссой
вспыхнул точечный мгновенный источник тепла
Слайд 86
Результатом действия элементарного точечного источника является приращения температуры
температура от движущегося
Изменение температуры в какой-либо точке может быть представлено суммой изменений температуры при распространении тепла от отдельных элементарных воздействий источника с учетом времени и места их приложения
Слайд 87Неограниченное теплопроводящее тело находится при нулевой начальной температуре. В момент времени
Подстановкой
выразим интеграл через функцию интеграла вероятности
2.2. Непрерывно действующий точечный источник в неограниченном теле
Слайд 88Принимая во внимание, что
получим:
Температуры всех точек тела
Тогда
и
Т.е., в предельном состоянии температуры тела более не меняются.Такое состояние процесса распространения тепла называется стационарным: тепло, вводимое источником, распространяется в неограниченном теле, не изменяя его температуры
Слайд 89 2.3. Непрерывно действующий точечный источник тепла постоянной
В момент времени
в точке О` находится
точечный источник,
действовавший
Слайд 90Элемент тепла
от точечного источника тепла, вспыхнувшего в момент времени
за
вызовет к моменту времени τ
приращение температуры
Температуру найдем, интегрируя :
(Чтобы учесть полупространство, мощность удваиваем)
Слайд 91В подвижной системе координат X, Y, Z,
связанной с источником,
Здесь
- длительность процесса распространения тепла элементарного источника, введенного в точке
С течением времени область повышенных температур достигает предельных размеров и только перемещается с источником. Такое состояние процесса называется предельным или установившимся, а температурное поле – квазистационарным.
(1)
Слайд 92Интеграл (1) в пределах от 0 до ∞ подстановкой
приводится к
(2)
После преобразований с учетом (2) уравнение предельного состояния процесса распространения тепла точечного источника постоянной мощности, движущегося с постоянной скоростью по поверхности полубесконечного тела принимает вид [Н.Н.Рыкалин]:
2.4. Уравнение предельного состояния процесса распространения тепла точечного источника постоянной мощности, движущегося с постоянной скоростью по поверхности полубесконечного тела
Слайд 932.5. Предельное состояние нагрева полубесконечного тела неподвижным непрерывно действующим источником тепла
При длительном нагреве полуограниченного тела непрерывно действующим источником теплоты процесс распространения тепла стремится к предельному состоянию. При этом решение для температуры в полубесконечном теле от неподвижного источника теплоты постоянной мощности q получим из ( ) при v=0
Т.е. температура в полуограниченном теле пропорциональна мощности источника q и обратно пропорциональна коэффициенту теплопроводности λ . При постоянных мощности и коэффициенте теплопроводности температура обратно пропорциональна расстоянию R от неподвижного источника теплоты. При этом изотермические поверхности представляют собой полусферы, а зависимости температуры от радиуса R – гиперболы.
Слайд 94
Ток короткого замыкания I= 250 А, а напряжение U=1 В. Мощность
λ= 360 Вт/(мК), Стальной плиты - 40 Вт/(м*К):
Неподвижный точечный источник на поверхности полубесконечного тела . Температура при коротком замыкании или точечной сварке.
Для неподвижного точечного источника (при v=0):
Слайд 952.6. Влияние скорости источника на распределение
температуры
температуры на поверхности полуограниченного тела
Согласно формуле
Для x<0, т.е. при x=-R , получим:
Для x>0, т.е. при x=R из уравнения следует :
Т.е. , с увеличением скорости температура убывает
быстрее
Слайд 96Влияние скорости перемещения точечного источника на распределение температуры предельного состояния по
При N=250 Вт, λ=40 Вт/(м*К), ω=0,000008 м*м/с
Слайд 97Распределение температуры от движущегося источника
в направлении оси OY , перпендикулярном
получим при x=0:
Т.е. в боковом направлении температура убывает медленнее,
чем перед источником в направлении его движения, но
быстрее, чем за источником.
1- сварочная ванна, 2 – изотермы, 3 – столбчатые кристаллиты.
Слайд 982.7. Непрерывно действующий точечный источник тепла постоянной мощности, неподвижный или движущийся
В неподвижной системе
координат
температурное поле имеет вид:
Граничные плоскости пластины
отдают тепло в окружающую
среду с нулевой температурой
при коэффициенте теплоотдачи
Слайд 99Множитель
учитывает теплоотдачу поверхн. в окружающую среду с нулевой температурой
Вводя время
и
координат, получим:
Для предельного состояния подстановкой
и обозначением
получим:
Бесселева функция от мнимого аргумента второго рода нулевого порядка
Слайд 100
С учетом выражения интеграла через бесселеву функцию
Здесь
расстояние от точки А до
положения О источника тепла
- аргумент функции
- коэффициент, учитывающий понижение
температуры пластины в окружающую среду в 1/с
α- коэффициент теплоотдачи
Слайд 103Значения функции K(u) могут быть определены по таблицам [8]
или графикам
Для неподвижного источника уравнение при v=0 примет вид
Слайд 104
В пластине тепловой поток больше стеснен, чем в полубесконечном теле .
Зависимость температуры от непрерывно действующего источника
в стальном полуограниченном теле и в стальной пластине, q=330 Вт.
Слайд 1052.8. Метод быстродвижущихся источников тепла
Н.Н.Рыкалиным было замечено, что при перемещении источника
При этом теплота распространяется в основном в направлении, перпендикулярном оси перемещения источника, что позволяет существенно упростить расчетные схемы, описывающие процесс распространения тепла.
В предельном случае v→∞ тепло источника распределено равномерно по оси перемещения и будет распространяться только перпендикулярно этой оси
Слайд 106На каждой изотерме температурного поля быстродвижущегося источника можно выделить участок, очертание
Слайд 107Температура от непрерывно действующего источника тепла, движущегося по поверхности пластины.
Поведем в
Для неподвижного точечного (линейного) мгновенного источника температура описывалась уравнением:
Так как тепло распространяется в направлении оси OY, заменим x на
Слайд 108Приращение количества тепла от точечного источника:
При этом интенсивность источника тепла
С учетом множителя
,учитывающего теплоотдачу
поверхности пластины, где
Уравнение процесса распространения тепла в пластине от быстродвижущегося линейного источника будет:
Слайд 1092.9. Температурное поле в полуплоскости от движущегося равномерно распределенного источника тепла
Схема к расчету температуры в полуплоскости от быстродвижущегося равномерно распределенного источника тепла
Слайд 111Схема к расчету температуры на укороченной передней поверхности от быстродвижущегося
Для условий резания (f=1 мм,
время нагрева стержня
τ=0,001 с
)
все тепло от источника поступает только в стержень (в стружку)
Слайд 112при определении приращения температуры в полуплоскости мощность источника тепла необходимо удвоить:
на
температуры
Слайд 1132.10. Оценка погрешностей и области применения метода быстродвижущихся источников
Поле относительных температур
Слайд 116Зависимость погрешности вычисления градиента температурного поля методом быстродвижущихся источников тепла от
Глубина проникновения тепла
при X>3
U(X,Y) < 0,02
Слайд 117
При
потоки вдоль оси y будут иметь место и
Воспользовавшись формулой
вычислим угол
Слайд 1192.11. Одномерное температурное поле от движущегося
источника тепла
τ″ = τ−τ′.
ξ
время τ″ выравнивания тепла:
τ′ -время после начала нагрева
Приращение температуры
Температура в точке x0 в момент времени τ
Слайд 120при τ → ∞ и, соответственно, при τ″ = τ−τ′ →
Зависимости температуры стержня от расстояния от движущегося источника тепла с плотностью теплового потока
Слайд 1213.1. Закономерности кристаллизации и затвердевания отливки в литейной форме
Схема распределения
3. ЗАКОНОМЕРНОСТИ ТЕПЛООБМЕНА ПРИ ЛИТЬЕ,
ОБРАБОТКЕ МЕТАЛЛОВ ДАВЛЕНИЕМ И СВАРКЕ
Слайд 122
Изменение плотности теплового потока и толщины затвердевшего слоя отливки с
Слайд 1233.2. Закономерности отвода теплоты в литейную форму
время остывания разобьем на три
Слайд 124Для первого интервала примем температуру на торце стержня постоянной,
равной средней
Количество теплоты, которое необходимо отвести для остывания расплава
до температуры плавления равно:
Зависимость отводимого количества теплоты от времени :
Приравнивая два выражения для количества теплоты ,
найдем время остывания до начала кристаллизации:
Слайд 126
Рис. Зависимость средней температуры расплава (отливки) от времени при толщине стенки
, литейный сплав – сталь:
Слайд 127
Закономерности отвода теплоты от заливки расплава до начала остывания отливки
при толщине стенки
отливки 10 мм,
формовочная смесь
– сырая с добавлением
опилок:
литейный сплав
– сталь:
Слайд 128
а)
Закономерности отвода теплоты от заливки расплава до начала остывания отливки
Слайд 129Охлаждение отливок в литейных формах после заливки происходит
от температуры заливки
Продолжительность выдержки в форме определяется толщиной стенки отливки, свойствами залитого сплава и литейной формы, температурой выбивки.
Закономерности остывания стальной (а) и алюминиевой (б) отливок пластин размерами 100*100*10 мм
Слайд 1303.3. Влияние теплофизических характеристик материалов песчаных и металлических литейных форм на
. Схематизация отвода тепла в литейную песчаную форму: 1, 2 - верхняя и нижняя половины литейной формы, 3 - стержень, 4 – полость (рабочая часть), 5,6 –верхняя и нижняя опоки.
Слайд 131Закономерности остывания стальной (а) и алюминиевой (б) отливок пластин размерами в
2 – количество теплоты до полного затвердения,
3 – количество теплоты до выбивки отливки,
4 – количество теплоты до температуры плавления
Слайд 132Теплофизические характеристики песчаной
формовочной смеси и некоторых литейных сплавов
Теплопроводность песчаной формовочной смеси
Теплофизические характеристики формовочной смеси снижаются при
добавлении опилок.
Слайд 133Для регулирования теплообмена в литейную форму встраивают обладающие высокой теплопроводностью элементы,
Влияние теплофизических характеристик смеси
Слайд 134Температуропроводность стальной формы в 40 раз больше, чем формы из сухой
время остывания при переходе от песчаной формы
к кокилю сокращается более, чем в 600 раз
Слайд 135литье алюминиевого кубика размерами 100 мм*100 мм*100 мм
Зависимости толщины затвердевшего слоя от
Литье в подогретый кокиль и в песчаные формы
Слайд 136 3.4. Теплообмен при литье под давлением
способ получения отливок из
сталей, максимально приближающий размеры и форму
отливки к размерам и форме готовой детали за счет нагнетания расплава в камеру прессования под давлением
Схема процесса изготовления отливок на машинах
с горизонтальной холодной камерой прессования
Слайд 137отливки из алюминиевого сплава размерами
10 мм*10мм*1 мм под давлением
Зависимости
литье под давлением
Слайд 1383.5. Теплообмен и температура при горячей прокатке
При соприкосновении холодного прокатного валка,
с нагретой до температуры
заготовкой тепло из заготовки интенсивно поступает в валок
- температура на поверхности контакта валка с заготовкой
- плотность теплового потока на торце стержня
Слайд 139Время τ нагрева «стержня»
В частности, при D=0,6 м, α=30°, v=1 м/с
При
средняя плотность теплового потока на участке контакта валка с заготовкой равна:
При b=2,3 м площадь контакта валка с заготовкой:
тепловой поток Ф, поступающий в валок:
Слайд 140Количество тепла Q1, поступившее в валки при прокате одной заготовки
Пусть масса
ширина b=2,3 м. Соответственно, длина полосы будет:
Время прокатки заготовки при скорости v=1 м/с:
Количество тепла Q1
в каждый из двух валков при прокате одной заготовки массой 50 тн поступит примерно по 7 МДж теплоты
Слайд 141Температуру за пределами участка вычислим путем наложения (суперпозиции) решений от равномерного
в конце первого оборота температура поверхности валка снизится с 500 до до 73,5 °С
Это вызовет дополнительное повышение контактной температуры примерно на 37 °С.
Слайд 142Еще через оборот валка остаточная поверхностная температура, вызванная первым контактом, снизится
однако появится повышение температуры от следующего контакта и суммарное повышение температуры от подогрева валка на втором обороте будет:
Колебания контактной температуры в рассматриваемом примере происходят с амплитудой около 400 °С и с частотой около 0,6 Гц.
Слайд 143При непрерывной прокатке заготовки контактная температура увеличивается. Так, например, за 4
Примерное изменение начальной температуры валка и контактной температуры с ростом числа оборотов валка при прокате одной заготовки
после проката заготовки и нескольких следующих друг за другом оборотов валка в контакте с заготовкой необходимо делать небольшой перерыв для выравнивания температуры.
Слайд 144При полном выравнивании этой теплоты по всей массе валка его начальная
Зависимость контактной температуры от числа прокатанных заготовок
С ростом количества прокатанных заготовок суммарное увеличение температуры валка, вызванное тепловыми потоками от нагретых заготовок, существенно увеличивается
Слайд 1453.6. Нагрев и охлаждение штампов при горячей штамповке
Пусть начальная температура
а начальная температура заготовки θз= 1000 °С.
При соприкосновении штампа с нагретой заготовкой контактная температура равна полусумме температур заготовки и штампа:
Схема к определению контактной температуры и тепловых потоков в штамп при горячей штамповке
штамповых сталей умеренной теплостойкости при температуре 600 -700 °С составляет около 350-250 МПа при достаточно высокой ударной вязкости
800 кДж/м2
Слайд 146Распределение температуры в глубине штампа
три группы штампов : 1- для
3- для скоростных молотов и гидровинтовых прессов
Средняя температура поверхностного слоя толщиной около 1 мм ниже, чем контактная температура (порядка 300 – 500 °С)
Слайд 147Плотность теплового потока
При
Влияние времени контакта на среднюю плотность теплового потока:
1
3- при штамповке на прессах и ГКМ
Слайд 148
3.7. Анализ теплового баланса при ручной дуговой сварке
Схема дуговой сварки. 1-деталь,
На электрод и заготовку подается напряжение, между ними зажигается устойчивый разряд электрического тока – электрическая дуга, обеспечивающая плавление электрода и заполнение сварного шва.
Слайд 149
сварочные токи до 200 А, мощности источника ( ≈до 3-4 кВт)
Схематизация
Слайд 151Пусть длина шва Lш , шов разделан фасками под 45° шириной
Количество тепла, необходимое для нагрева этого объема металла
до температуры плавления:
Количество тепла, необходимое для плавления этого объема металла
Время сварки τ
тепловой поток Фпл, необходимый для плавления металла:
1. Тепловой поток Фпл, необходимый для плавления металла
Слайд 1522.Тепловой поток, поступающий в сварочный электрод
Электрод - полуограниченный изолированный с поверхности
торец которого находится при температуре плавления электрода.
Количество теплоты :
Тепловой поток в электрод:
3. Тепловой поток, поступающий в деталь
длина источника тепла :
Слайд 153
Т.к.
Израсходованная длина электрода:
скорость перемещения электрода вдоль него, необходимая для сохранения
Слайд 154Баланс тепловых
потоков при
ручной дуговой
сварке
Соотношение
скоростей
перемещения
и подачи
Слайд 155Схема автоматической дуговой сварки
сварочные токи до 2000 А, мощности источника
3.8. Тепловые балансы при различных термических способах сварки
Слайд 156Баланс тепловых
потоков при
автоматической
дуговой сварке.
(Основная
мощность - на
плавление)
Соотношение
скоростей
перемещения
и подачи электрода
Слайд 157Схема сварки в защитных газах неплавящимся электродом при прямой полярности с
1 – присадочный пруток, 2- сопло, 3 – токопроводящий мундштук, 4 – корпус горелки, 5-неплавящийся вольфрамовый электрод, 6 – рукоять горелки, 7- атмосфера защитного газа, 8 – сварочная дуга, 9 –ванна расплавленного металла.
Слайд 158 Баланс тепловых потоков при сварке алюминиевых заготовок в защитных газах
соотношение скоростей перемещения и подачи электрода
Напряжение U=10 В, ток I= 400 А, η=0,6, N=2,4 кВт.
(Основная мощность –
в деталь)
Слайд 159Схемы получения плазменной струи, выделенной из дуги (а), и плазменной дуги,
1 – дуга,
2 –вольфрамовый
электрод,
3 – керамическая
прокладка,
4 - корпус горелки,
5 – сопло,
6 – плазменная струя,
7 - заготовка
Слайд 160Баланс тепловых потоков при плазменной сварке
стальная заготовка, ток I= 10A, U=20
почти вся мощность отводится в виде теплового потока в деталь (из-за градиентов)
Слайд 161Схема электрошлаковой сварки
1-трубы ползуна,
2 – сварочная ванна расплавленного металла,
3
4 – сварочная проволока,
5 – мундштук,
6 – основной металл заготовок,
7 – ползуны
8 – затвердевший сварной шов,
9 – вводная планка,
10 - выходная планка
Слайд 162Баланс тепловых потоков при электрошлаковой сварке
Стальная заготовка
при токе I= 1000
Соотношения между скоростями подачи электродной проволоки (диаметром 3 мм пучком из 3 шт.) и перемещения ползунов
Слайд 1633.9. Температура при электрической контактной стыковой сварке
1 – неподвижная плита,
2,
4 – подвижная плита,
5 – сварочный трансформатор,
6, 7 – свариваемые заготовки
Схема контактной стыковой сварки
Электрическое напряжение подается на зажимы 2 и 3 через сварочный трансформатор 5.
Подвижная плита 4 перемещается в направлении неподвижной плиты 1 до осуществления контакта заготовок 6 и 7 и сжимает заготовки с усилием Р
Слайд 164
Температура в плоскости контакта (т.е. при x=0) согласно формуле (1.64):
Зависимость контактной
Слайд 165Зависимости тока I и усилия Р от времени нагрева
При одном импульсе
при трех импульсах тока:
Мощность в 2,2 раз больше, чем при одном импульсе
Слайд 1663.10. Температура и количество теплоты
при конденсаторной сварке
Схема конденсаторной сварки: 1
Конденсаторная сварка осуществляется за счет энергии,
накопленной в батарее конденсаторов при
их зарядке от источника постоянного тока:
Слайд 167Зависимости температуры от времени разряда при конденсаторной сварке стальных, медных и
время разрядки конденсаторной батареи очень мало и измеряется тысячными или десятитысячными долями секунды
Слайд 168Температура стыка свариваемых заготовок рассчитывается по формулам
при небольшой энергии (Q=0,02-0,05
Слайд 169при уменьшении времени действия источника тепла от 1 с до 0,001
Зависимость количества тепла от времени действия источника, необходимого для нагрева торцов стальной проволоки диаметром 0,2 мм до температуры плавления
Слайд 1703.11. Температура при сварке трением
. Принципиальные схемы сварки трением: а)-вращение одной
Сварка трением осуществляется за счет адгезии (схватывания) контактируемых поверхностей
Слайд 171 Плотность теплового потока (или удельная мощность трения q) на поверхности
Схема распределения температуры по торцу заготовки при сварке трением
При постоянном радиусе температура рассчитывается по формулам:
Слайд 172Зависимости температуры от времени нагрева при диаметрах трущихся заготовок от 5
Сила Р определится по формуле:
где μ - коэффициент трения, v – скорость трения (в средней части заготовки или на ее периферии, P – осевая сила сдавливания заготовок.
Слайд 173
Решение
может быть применено, для оценки температурного поля при точечной сварке
Схемы контактной точечной сварки:
а) двусторонней,
б) односторонней
3.12. Температура при электрической контактной точечной сварке
Слайд 174Зависимости температуры от расстояния от источника тепла в различные моменты времени.
В некоторой окрестности точки, в которой действует точечный источник тепла, температура превышает температуру плавления и излишнее тепло идет не на повышение температуры, а на расплавление металла
Слайд 175Стремление температуры от точечного источника к предельным значениям . Условия те
1) - при меньшей мощности источника осуществлять прогрев и расплавление металла, ориентируясь на предельное температурное состояние.
2) -при большей мощности сварку производить, на более жестком режиме, но отключать подачу тока, не доводя температуры до предельных значений.
При
Для полупространства мощность удваиваем
Слайд 176Зависимости температуры от расстояния от источника тепла в различные моменты времени.
Слайд 1773.13. Температура при электрической контактной шовной
сварке
а) – двусторонней,
1- заготовки, 2 – электроды, 3 – медная подкладка
Слайд 178Температура в окрестности движущегося точечного источника может быть вычислена по формуле:
или
Слайд 1813. 14. Температура при ультразвуковой сварке
1 – магнитострикционный преобразователь,
продольных упругих колебаний, 3 – рабочий инструмент,
4 – наконечник рабочего инструмента, 5 – свариваемые
заготовки, 6 – опора
Слайд 182
Установившееся распределение температуры в стальной
пластине δ=1 мм, b=0,0028 1/с, ω=8 мм2/с,
Температура от неподвижного
точечного источника на поверхности пластины:
Слайд 183Источники теплоты:
1. зона стружкообразования,
2. участок контакта стружки и режущего
на передней поверхности,
3. участок контакта застойной зоны и фаски износа режущего лезвия по задней поверхности с деталью.
4. ЭЛЕМЕНТЫ ТЕПЛОФИЗИКИ РЕЗАНИЯ
Вся работа, затрачиваемая при резании на деформацию и трение, превращается в теплоту.
Это было доказано еще в начале двадцатого века (в 1905 г) опытами Н.Н.Савина.
Он сверлил деталь, помещенную в калориметр, измеряя крутящий момент (и мощность резания) с помощью динамометра и количество образованной при сверлении теплоты с помощью калориметра. Работа резания, измеренная с помощью динамометра, оказалась эквивалентной теплоте, измеренной калориметром.
4.1.Схематизация теплообмена в зоне резания
Слайд 185Для расчета температуры деформации необходимо оценить мощность (удельную работу) тепловыделения и
Наибольшее количество теплоты при резании образуется в зоне стружкообразования. Эта теплота равномерно выделяется внутри материала, почти вся уносится нагретым материалом в стружку.
В результате повышения теплосодержания (энтальпии) и с учетом удельной объемной теплоемкости обрабатываемого материала стружка равномерно прогревается до температуры деформации θд.
При этом используются сведения об угле наклона зоны стружкообразования (или усадке стружки), а также эмпирические или теоретические сведения об удельных касательных силах в зоне стружкообразования
Слайд 1864.2. Анализ тепловых потоков, поступающих в стружку и в инструмент при
Для анализа соотношения тепловых потоков стружку и в режущее лезвие будем считать температуру на передней поверхности равномерно распределенной и известной.
Плотность теплового потока, поступающего в стержень через его торец при постоянной температуре торца , обратно пропорциональна времени нагрева
Слайд 187Время нагрева стержня , выделенного в стружке, выразим через усадку стружки
Отношение плотностей тепловых потоков, поступающих в резец и в стружку:
Слайд 188Теплофизические характеристики обрабатываемого и инструментального материалов оказывают относительно небольшое влияние на
Зависимость отношения тепловых оттоков в резец и в стружку от времени резания при
Слайд 189
. Схема к определению теплообмена между полуограниченным стержнем и быстродвижущейся полуплоскостью
Принимая для типичных условий обработки сталей твердосплавными инструментами =1, v = 1 м/с, l = 1 мм, τ = 10 с, находим, что
Слайд 1904.3. Тепловые потоки в инструмент и в стружку при торцовом
. Схема торцового фрезерования:
а) – в основной плоскости,
б) – в рабочей плоскости, в) - в плоскости стружкообразования
Слайд 191
Схема к определению максимального угла контакта зуба фрезы с заготовкой
для D=60
Или поправочный коэффициент Ки=0,82
Слайд 1924.4. Тепловой поток от условной плоскости сдвига в обрабатываемую заготовку и
Схема к расчету теплового потока от условной плоскости сдвига в обрабатываемую заготовку
источник тепла плотностью
движется в направлении оси х, перпендикулярном условной плоскости сдвига со скоростью
Пи этом формула для установившейся температуры стержня от движущегося источника:
Слайд 194
Тепловой поток в деталь от плоскости сдвига
при ctgϕy ≈ 1,74
Pe = 40 – 140
Фд/Ф0= 0,044….0,012
Слайд 1954.6. Калориметрический метод измерения тепловых потоков, поступающих в обрабатываемую заготовку
Схема калориметра:
1 - внешний сосуд; 2 - термометр;
3 - калориметрический стакан;
4 - мешалка;
5 – трансформаторное масло;
6 – втулка после обработки резанием
После обработки лопаточным резцом деталь помещают в ядро калориметра.
Слайд 196Схема резания лопаточным резцом с обратными срезами для измерения тепловых потоков,
Работа сил на задних поверхностях может быть определена измерением количества тепла,
поступившего в деталь.
Тепловой поток Ф, поступивший в деталь, определяется по теплосодержанию детали Q и времени резания τр:
Слайд 197По истечении некоторого времени Δτ температуры ядра калориметра и детали выравниваются
Типичные кривые измерения температуры ядра калориметра при помещении в него детали после опыта (а) и при охлаждении (б)
Слайд 198Теплосодержание Q детали (втулки) определяется по формуле:
где K - теплоемкость калориметра,
Температурная поправка Δθ в ряде случаев может достигать 10 - 15 % от θ1 - θ0 и поэтому для повышения точности калориметрических измерений ее необходимо обязательно учитывать. Это особенно важно при проведении нескольких, следующих друг за другом измерений.
Слайд 199Для оценки теплоотдачи калориметра в окружающую среду в ядро калориметра вводится
Экспериментально в течение 8-10 часов определяется кривая охлаждения ядра ″θ0* −τ″ (рис. … б), кривая аппроксимируется экспоненциальной функцией вида :
Снижение температуры Δθ за время Δτ (см. рис. ):
Слайд 200Средняя температура главного периода измерения
где χ- константа, определяемая из экспериментальной
Если время опыта не менее 0.5 с, погрешностями теплообмена можно пренебречь
Слайд 2014.7. Результаты измерения тепловых потоков, поступающих в обрабатываемую заготовку
Схема потоков
Слайд 202Экспериментальные результаты (рис.) подтверждают предположения о том, что тепловой поток Ф0,
. Влияние скорости резания на тепловые потоки в деталь при точении стали 45: МПа, резец - Т15К6, а=0,35 мм, b=1 мм, 1- h=0,1 мм, 2 - h=0,2 мм, 3 - h = 0,35 мм
Слайд 203Опыты по определению тепловых потоков от застойной зоны проводились острыми резцами
Зависимости теплового потока Ф от высоты застойной зоны при точении с толщиной среза a=0,35 мм :а) - сталь 45, резец Т15К6, v: 1 - 50 м/мин, 2 - 100 м/мин, 3 - 200 м/мин, б) - ХН67МВТЮ-ВД, резец ВК8,: 1 - 2,0 м/мин, 2 - 5,0 м/мин, 3 - 10 м/мин, 4 - 20 м/мин
Слайд 204Опыты по определению тепловых потоков от фаски износа h3 (рис. )
Зависимости теплового потока Ф от ширины фаски износа при точении с толщиной среза a=0,35 мм :а) - сталь 45, резец Т15К6, v: 1 - 50 м/мин, 2 - 100 м/мин, 3 - 200 м/мин, б) - ХН67МВТЮ-ВД, резец ВК8, v : 1 - 2,0 м/мин, 2 - 5.0 м/мин, 3 - 10 м/мин, 4 - 20 м/мин
Слайд 205Плотности тепловых потоков qФ вычислялись графическим дифференцированием потока Ф по площади
или в безразмерном виде:
Зависимости плотности теплового потока q от высоты застойной зоны при точении с толщиной среза a=0,35 мм: а) - Сталь 45, резец Т15К6, v: 50 - 200 м/мин, б) - ХН67МВТЮ-ВД, резец ВК8, v: 1 - 5,0 м/мин, 2 - 10 м/мин, 3 - 20 м/мин
Слайд 206 Зависимости плотности теплового потока q от ширины фаски износа при
Слайд 2074.8. Температура быстродвижущейся полуплоскости от равномерно распределенного источника тепла
Ранее было широко распространено предположение о равномерном распределении удельных касательных сил (и плотностей тепловых потоков) по ширине фаски износа резца с обрабатываемой заготовкой, и на участке пластического контакта стружки с резцом
Слайд 208расчет температуры на участке пластического контакта стружки с резцом и на
Схема к расчету температуры в полуплоскости,
быстродвижущейся относительно равномерно распределенного
источника тепла постоянной плотности теплового потока
Слайд 209температурное поле в полуплоскости описывается решением
Или более простым решением :
плотность теплового
Слайд 210Температуру торца стержня определим по формуле
схема к расчету приращения температуры
Слайд 211Наибольшая температура будет иметь место при y=f в точке (0,f). С
при точении отожженных сталей, имеющих относительно невысокую твердость:
Слайд 212. Распределение температуры по укороченной передней поверхности при точении стали 12ХН3А
Слайд 2134.9. Температура на границе быстродвижущейся полуплоскости от неравномерно распределенного источника тепла
Схема
Слайд 214Формулу (…..) преобразуем к виду:
Участок упругого контакта стружки с резцом разобьем
значения плотности теплового потока q
Равномерно распределенный по длине участка пластического контакта (0, 1) источник теплоты продлим на участок упругого контакта (1, 2) и аппроксимируем линейно убывающий источник тепла равномерно распределенными источником и стоками
Слайд 215Схема замены линейно убывающего источника теплоты равномерно распределенными источником и стоками
При этом :
или
Слайд 216значения гомологических температур :
Температуру θ передней поверхности вычислим по формуле:
при
Слайд 217Таблица к расчету температуры на участке упругого контакта
На участке пластического
Точение стали 45 HB=1800 МПа, δ=0,2 , m=0,15, резцом Т5К10 γ=10°, ϕ=70°, со скоростью резания v= 65 м/мин, глубиной t=5 мм, подачей s=0,4 мм/об.
Слайд 2184.10. Температура задней поверхности от равномерно распределенных на участке застойной
Схема тепловых потоков на задних поверхностях застойной зоны и фаски износа
Для резца без упрочняющей фаски длина участка застойной зоны по данным [ Н.Н.Зорев ] при рациональных режимах резания (порядка 800 – 900 °С) высота застойной зоны приблизительно равна 0,3a.
что безразмерная плотность теплового потока определяется соотношением:
Слайд 219Температура на участке застойной зоны рассчитана по формуле :
Наибольшая
Зависимость температуры режущей кромки от толщины срезаемого слоя при точении стали HB=1800 МПа, δ=0,2 , m=0,15, резцом Т5К10 γ=10°, ϕ=70°, , со скоростью резания v= 65 м/мин (кривая 1) и v=130 м/мин (кривая 2) , глубиной t=5 мм, подачей s=0,4 мм/об.
Слайд 220температуру на фаске износа определим суммируя приращения температуры от источника и
Распределение температуры по фаске износа задней поверхности при точении стали HB=1800 МПа, δ=0,2 , m=0,15, резцом Т5К10 γ=10°, ϕ=70°, со скоростью резания v= 65 м/мин , глубиной t=5 мм, подачей s=0,4 мм/об.
Слайд 221Зависимость температуры задней поверхности от ширины фаски износа при точении стали
2- без учета застойной зоны.
Большие расхождения в расчетных температурах с учетом и без учета источника теплоты на участке застойной зоны имеют место вблизи режущей кромки, т.е. для «острого» резца
Слайд 2225. СОВЕРШЕНСТВОВАНИЕ РАСЧЕТА ТЕМПЕРАТУРЫ ПРИ РЕЗАНИИ НА ОСНОВЕ ТЕРМОМЕХАНИЧЕСКОГО ПОДХОДА
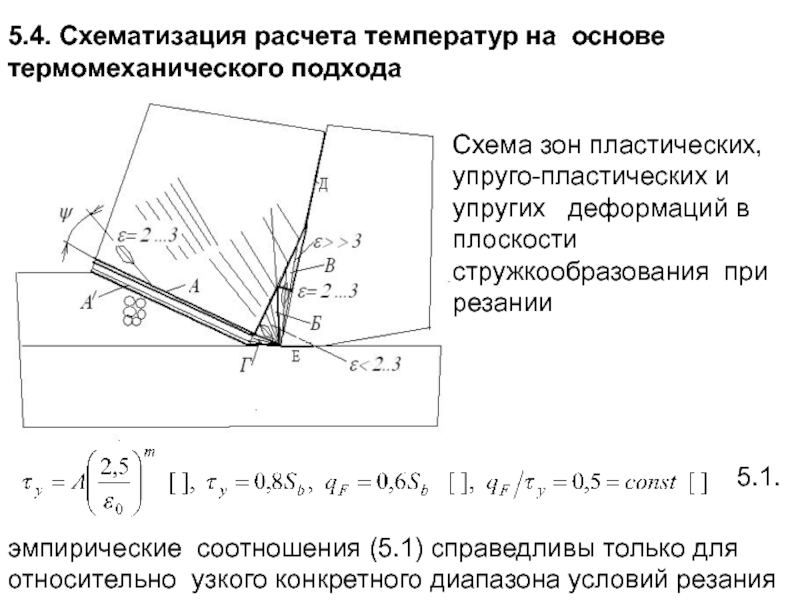
5.1.
Схема зон пластических, упругопластических и упругих деформаций в плоскости стружкообразования при резании
Слайд 224Распределение расчетной температуры по укороченной передней поверхности при точении стали 60
Резание стали с наростом на режущем лезвии при невысоких температурах
Слайд 225Распределение отношения предела текучести на сдвиг к действительному пределу прочности при
Распределение расчетной температуры по укороченной передней поверхности при точении стали 60 резцом Т5К10 , γ=10°, ϕ=70°, s=1,2 мм/об, t= 10 мм, при ζ=2 с учетом влияния температуры на удельные касательные силы при скорости резания v=60 м/мин (Ре=140).
Слайд 226Расчетные распределения температуры и плотностей тепловых потоков при точении стали 1-
Слайд 228Зависимость удельной работы деформации в адиабатических условиях деформирования от деформации
Слайд 229Зависимость предела текучести от деформации при резании для адиабатических условий деформирования
Сопоставление
отношения предела текучести на сдвиг к пределу прочности при резании и растяжении от деформации
Слайд 230зависимость предела текучести на сдвиг от деформации описывается выпуклой кривой, имеющей
В зонах Б и Г (рис….) деформации более однородны (более равномерно распределены), вследствие чего влияние скорости деформации будет несколько более высоким:
Максимальных значений пределы текучести в зоне А стружкообразования и в зонах Б и Г достигают в стационарных точках
Слайд 2315.3. Влияние локализации деформаций у конечной границы зоны стружкообразования на температуру
Зависимость отношения предела текучести на сдвиг к действительному пределу прочности при точении стали 45
Слайд 232
температура деформации:
При этом отношение среднего предела текучести к действительному пределу прочности
После достижения стабилизации предела текучести, т.е. при часть деформации локализуется в узкой области вблизи конечной границы зоны стружкообразования
Слайд 233При этом дальнейшее увеличение деформации может происходить в узкой зоне (в
Таким образом, закономерности упрочнения и разупрочнения связаны с изменением схемы зоны стружкообразования
При увеличении деформации температура деформации возрастает, а интенсивность упрочнения деформируемого материала уменьшается.
Стабилизации зависимости предела текучести от деформации способствуют уменьшение показателя деформационного упрочнения m , повышение прочности материала (A1) .
При достижении максимума предела текучести деформируемый материал не упрочняется с ростом деформации, т.е. обладает свойствами идеально пластического тела.
Слайд 234 При достижении условий локализации деформаций зависимость предела текучести от текущего
Слайд 235Влияние локализации деформаций в узкой зоне на зависимости удельной работы от
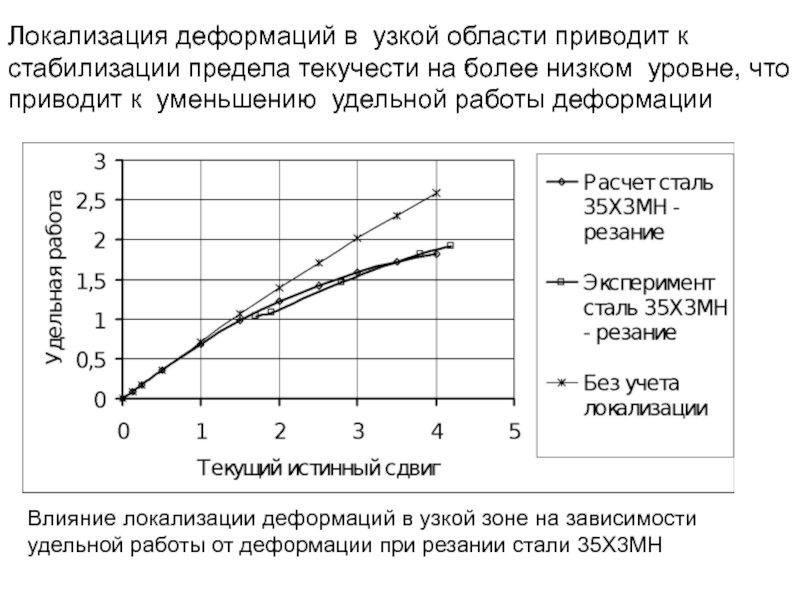
Локализация деформаций в узкой области приводит к стабилизации предела текучести на более низком уровне, что приводит к уменьшению удельной работы деформации
Слайд 236Деформацию
вычислим, аппроксимируя кривую
течения параболой при пересечении ее с прямой
Если
, то локализация деформаций начинается уже при
Удельная работа с учетом локализации будет:
Слайд 2375. СОВЕРШЕНСТВОВАНИЕ РАСЧЕТА ТЕМПЕРАТУРЫ ПРИ РЕЗАНИИ НА ОСНОВЕ ТЕРМОМЕХАНИЧЕСКОГО ПОДХОДА
5.1.
Схема зон пластических, упруго-пластических и упругих деформаций в плоскости стружкообразования при резании
Слайд 238Удельные касательные силы в зоне стружкообразования и на передней поверхности режущего
Схема зоны деформации и сил резания в плоскости стружкообразования
Слайд 240, γ=10°, ϕ=70°, s=1,2 мм/об, t= 10 мм, при ζ=2,
Распределение расчетной температуры по укороченной передней
поверхности при точении стали 60 резцом Т5К10
Расчетная температура для условий точения закаленной стали 60 после отпуска до твердости HB=2800 МПа с подачей s=1,2 мм/об, с глубиной резания t=10 мм
Слайд 241Схема к заданию плотностей тепловых потоков на передней и задней поверхностях
Слайд 242 Результаты расчета температуры существенно завышены, так как температура не может
Ошибки расчета связаны, главным образом, с завышенной оценкой отношения предела текучести к действительному пределу прочности q F /Sb.
С повышением температуры это отношение должно снижаться .
При этом вследствие разупрочнения материала температура на участке пластического контакта будет увеличиваться значительно медленнее, т.е. ее рост почти стабилизируется
Слайд 243Расчетные распределения температуры и плотностей тепловых потоков при точении стали 1-
Слайд 246Зависимость удельной работы деформации в адиабатических условиях деформирования от деформации
Слайд 247Зависимость предела текучести от деформации при резании для адиабатических условий деформирования
Сопоставление
отношения предела текучести на сдвиг к пределу прочности при резании и растяжении от деформации
Слайд 248зависимость предела текучести на сдвиг от деформации описывается выпуклой кривой, имеющей
В зонах Б и Г (рис….) деформации более однородны (более равномерно распределены), вследствие чего влияние скорости деформации будет несколько более высоким:
Максимальных значений пределы текучести в зоне А стружкообразования и в зонах Б и Г достигают в стационарных точках
Слайд 249 При отсутствии локализации деформаций у конечной границы зоны стружкообразования на
Зависимость отношения предела текучести на сдвиг к действительному пределу прочности при точении стали 45
Слайд 250При
адиабатические условия деформирования переходят в изотермические
Зависимости отношения предела текучести
Слайд 251Влияние локализации деформаций в узкой зоне на зависимости удельной работы от
Локализация деформаций в узкой области приводит к стабилизации предела текучести на более низком уровне, что приводит к уменьшению удельной работы деформации
Слайд 252безразмерная удельная работа будет:
температура деформации
отношение среднего значения предела текучести
Т. о. вследствие перехода к изотермическим условиям деформации произошло разупрочнение деформируемого материала, выразившееся в уменьшении отношения удельных касательных сил к действительному пределу прочности в рассмотренном примере примерно на 10%.
Слайд 2545.4. Схематизация расчета температур на основе термомеханического подхода
Схема зон пластических,
эмпирические соотношения (5.1) справедливы только для относительно узкого конкретного диапазона условий резания
5.1.
Слайд 255Схема к заданию краевых условий на передней и задней поверхностях режущего
зависимость предела текучести от координаты y будет иметь интервалы
возрастания и убывания
,
Слайд 256
где
Максимальное значение безразмерного предела текучести :
Температуру в начале интервала разупрочнения примем
Определяющее уравнение для интервала разупрочнения обрабатываемого материала на передней поверхности представим в виде:
эмпирический показатель степени отражает и непосредственное разупрочняющее влияние температуры и косвенное упрочняющее влияние температуры через скорость деформации
Слайд 257В интервале разупрочнения для любой координаты y=vτ температуру
быстродвижущегося «стержня»,
плотность теплового потока при температуре деформации равна максимальному пределу текучести , а при стремлении температуры к температуре плавления стремится к нулю:
Показатель степени B q j,обычно находится в пределах от 1 до 1,5 и должен быть уточнен по имеющимся экспериментальным данным о температуре или об удельных касательных силах.
Слайд 258Распределение температуры по ширине фаски износа задней поверхности от равномерно распределенного
Прочие условия те же .
1- без учета застойной зоны, 2 – с учетом застойной зоны
При расчете температуры на задней поверхности режущего лезвия в начале застойной зоны Г задается максимальное значение плотности теплового потока
Слайд 259РАЗВИТИЕ СХЕМАТИЗАЦИИ РАСЧЕТА ТЕМПЕРАТУР И УДЕЛЬНЫХ КАСАТЕЛЬНЫХ СИЛ ПРИ РЕЗАНИИ НА
Слайд 260Предельные распределения температуры и плотности тепловых потоков
При малых температурах (220 °С)
При увеличении температуры до 1250 °С при резании сталей плотность тепловых потоков снижается до 0,2 -0,4
Слайд 261Схема итераций при расчете температуры и предела текучести на передней поверхности
Слайд 266Распределения температуры и предела текучести по длине контакта
при точении стали
HB=2000 Мпа
S=0,15 мм/об, t=4 мм, ζ=2
Слайд 269Распределения температуры и безразм. плотности теплового потока по задней грани
, V=25 м/мин
V=250 м/мин
Слайд 271Метод полуискусственной (защемленной) термопары Я.Г.Усачева (1905 г.)
1 – резец,
2
3 - термопара, 4 – милливольтметр,
5 - изолятор
Слайд 272Метод естественной термопары
1- обрабатываемая деталь,
2 – режущая пластина,
3 – державка резца,
4
6- усилитель, 7 – токосъемник,
8 – провода, 9 – изоляторы.
токосъемник
(предложен Е. Гербертом и К. Готвейном)
температура резания,
Слайд 273Сопоставление экспериментальных и расчетных температур резания
Эксперимент Н.В.Талантова
Эксперимент А.Д.Макарова
Слайд 274Сталь 40, γ=10°, ϕ=45°
Эксперимент Н.Н.Зорева
Сопоставление экспериментальных и расчетных температур
Слайд 275Сталь 40, γ=10°, ϕ=45°
Эксперимент Н.Н.Зорева
Сопоставление экспериментальных и расчетных температур
Слайд 276Сталь 40, γ=10°, ϕ=45°
Эксперимент Н.Н.Зорева
Сопоставление экспериментальных и расчетных температур
Слайд 277Эксперимент Н.Н.Зорева при точении стали 20,
HB=1260 Мпа, σb =450 МПа, δ=30%,
Сопоставление экспериментальных и расчетных температур резания
Слайд 279метод измерения температуры по структурным превращениям в инструментах из быстрорежущей стали
Температурное поле в резце при точении низкоуглеродистой стали с подачей 0,5 мм/об и скоростью 91 м/мин после 30 с резания
при температуре, превышающей 600 °С, быстрорежущая сталь «переотпускается». После резания в течение 10 – 30 с под влиянием нагрева микротвердость быстрорежущей стали уменьшается и структура стали претерпевает превращения, которые можно проследить с помощью металлографического или электронного микроскопов





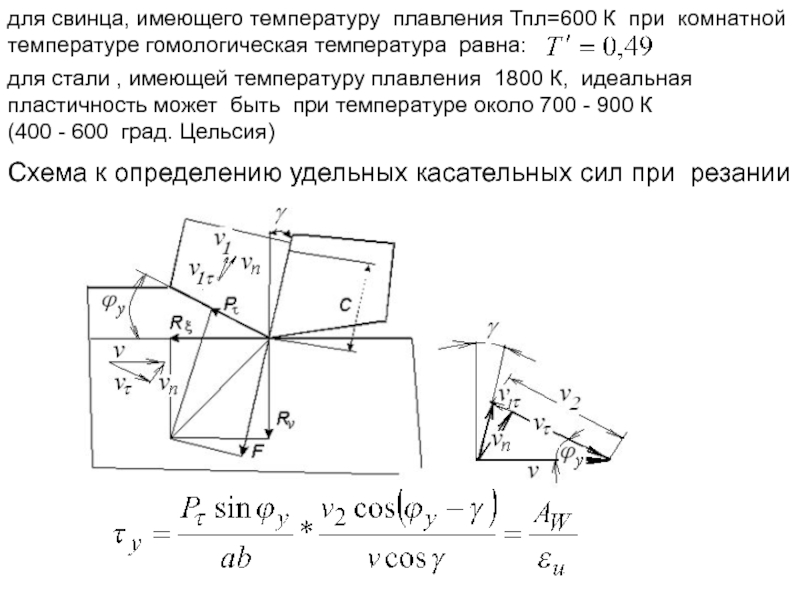
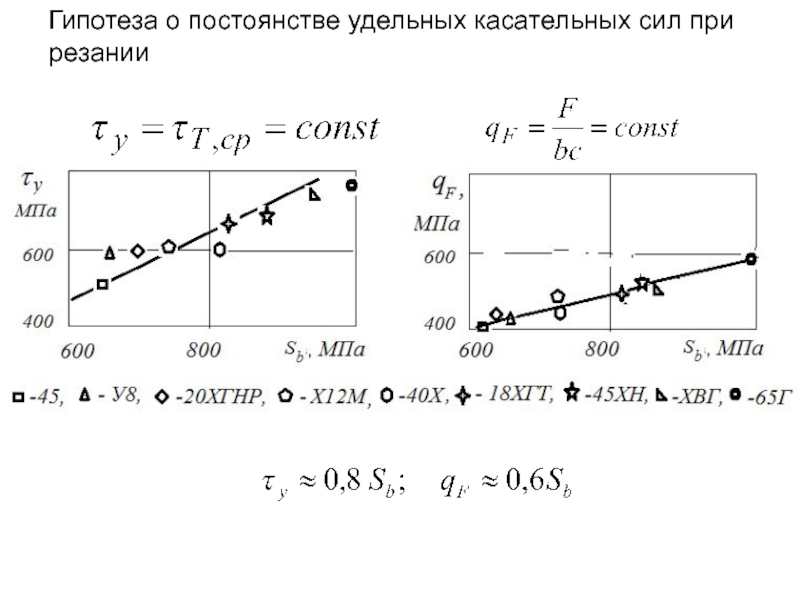
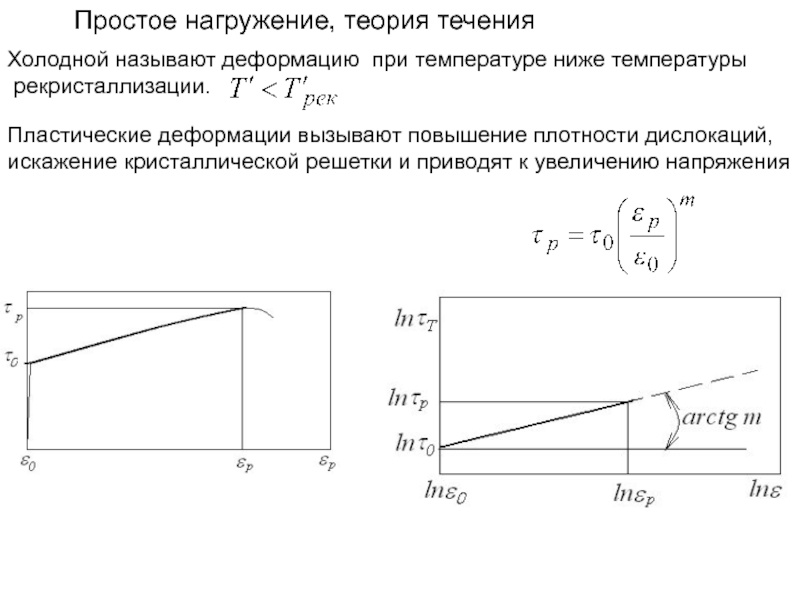
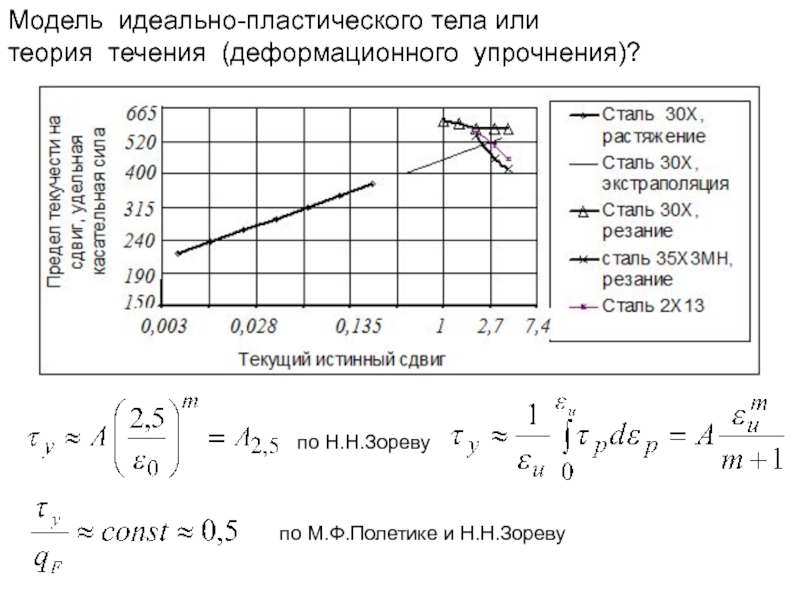
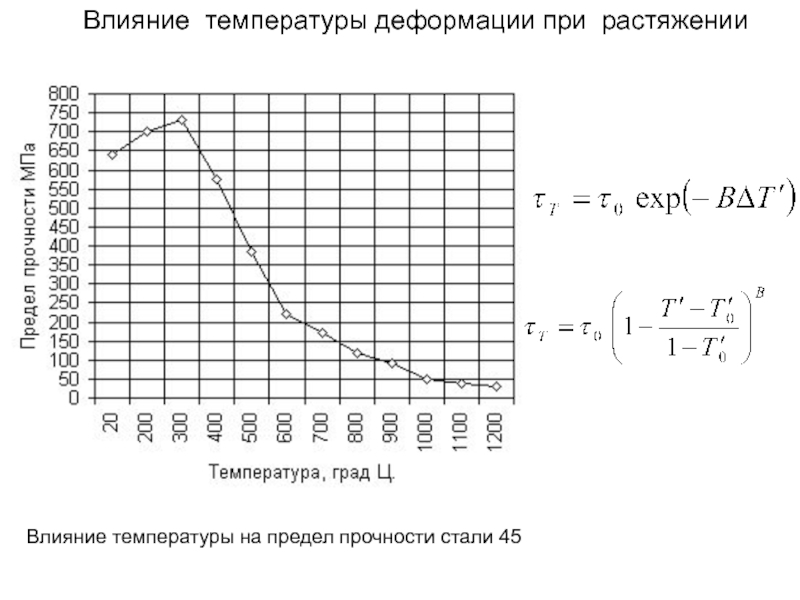
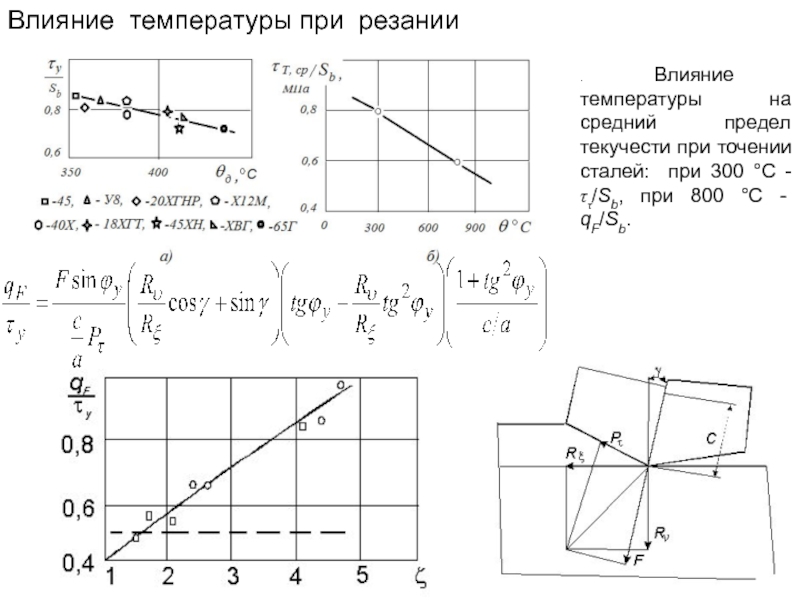
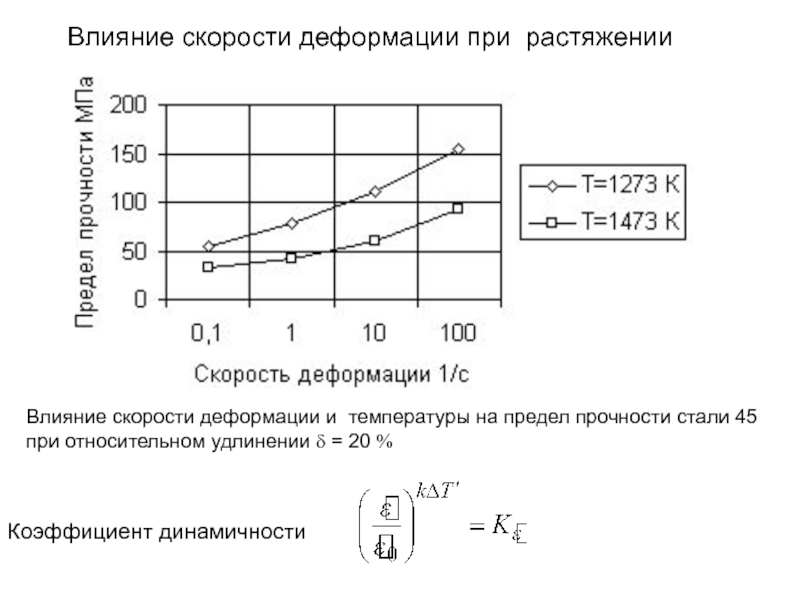
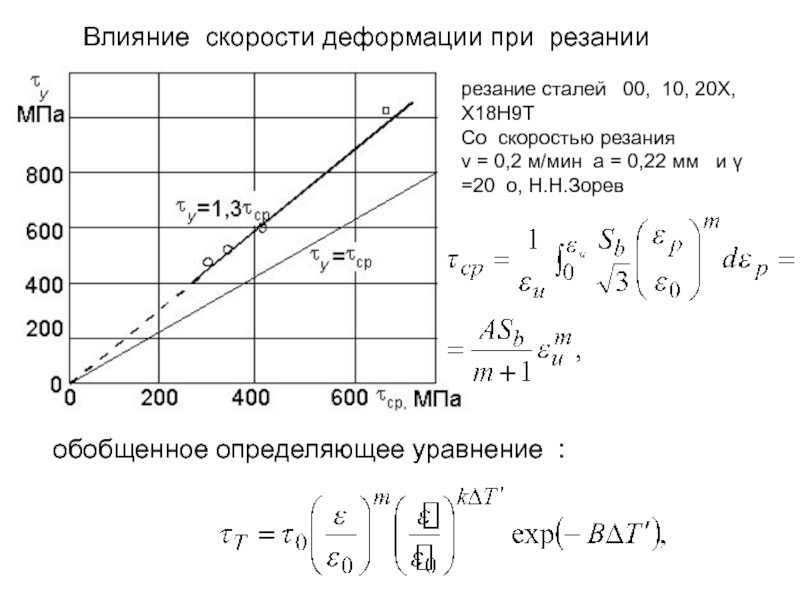
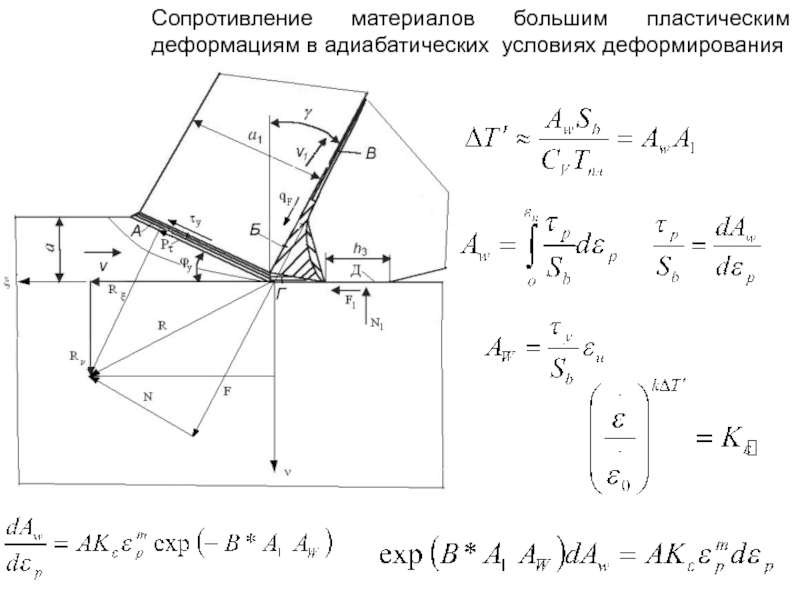
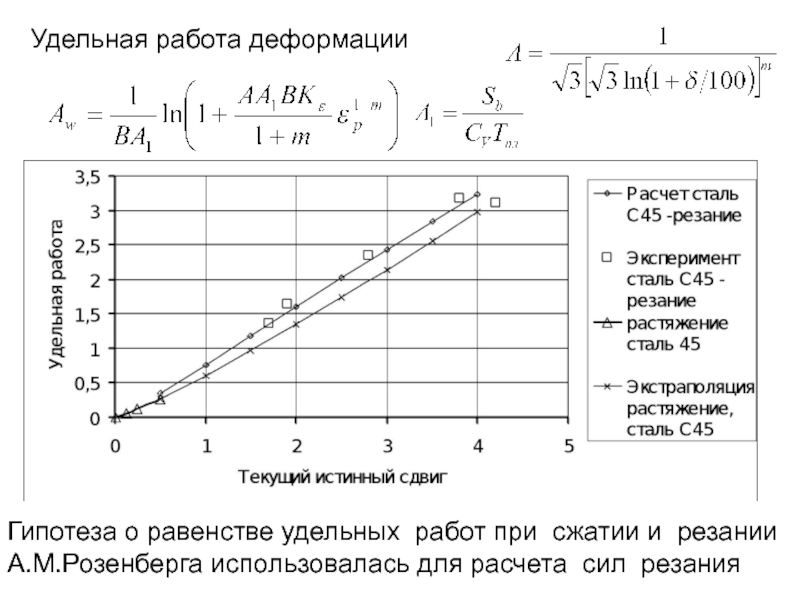
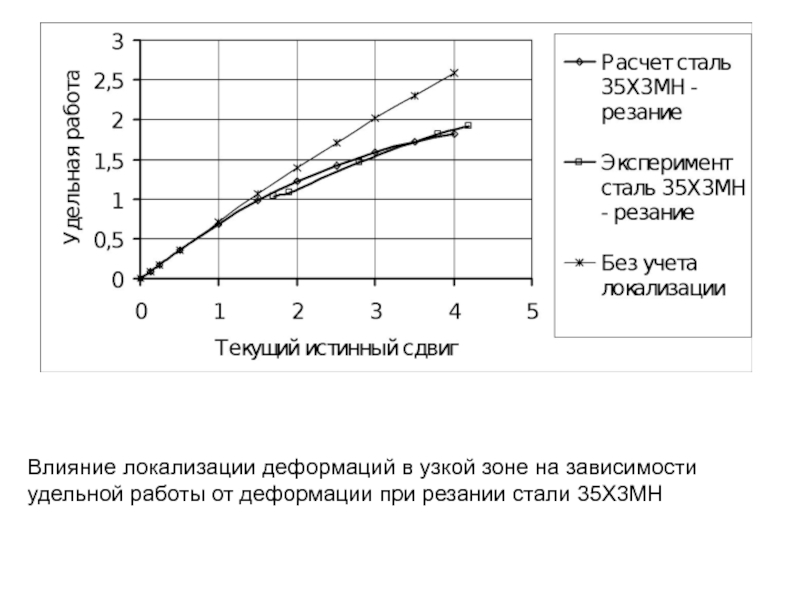
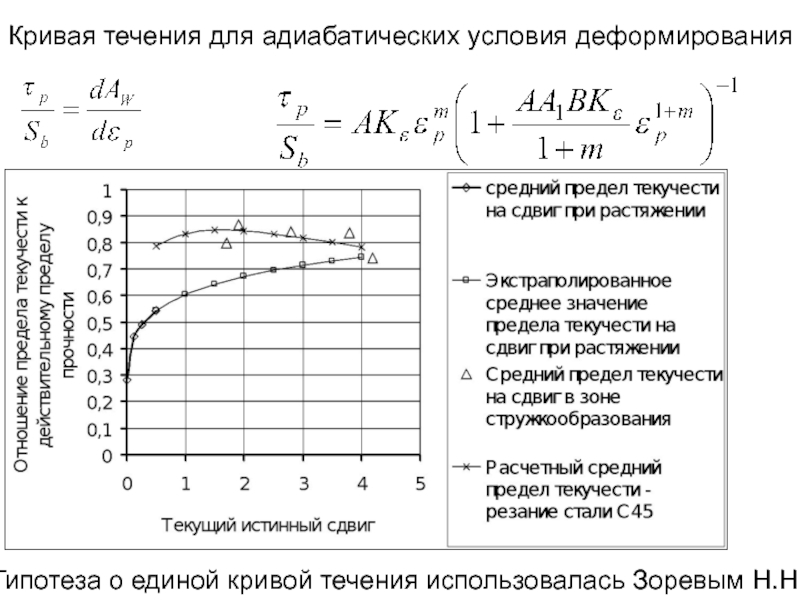
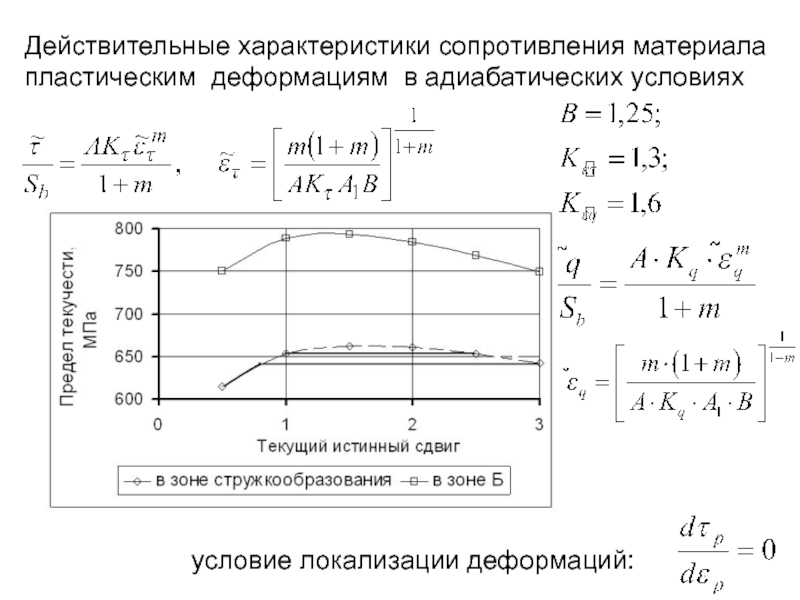
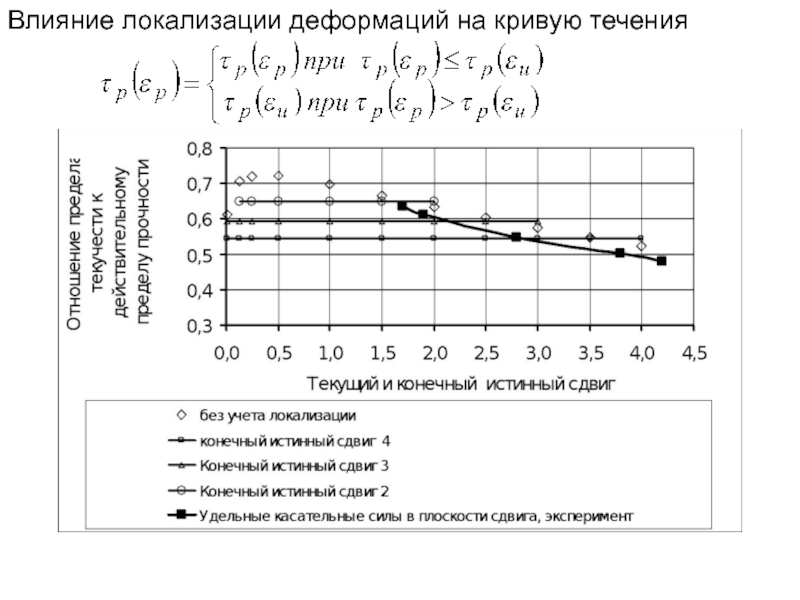
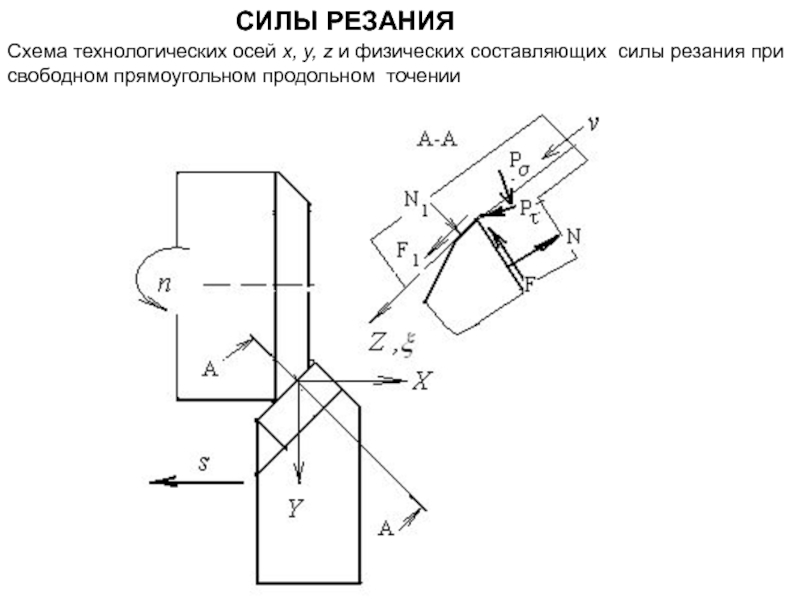
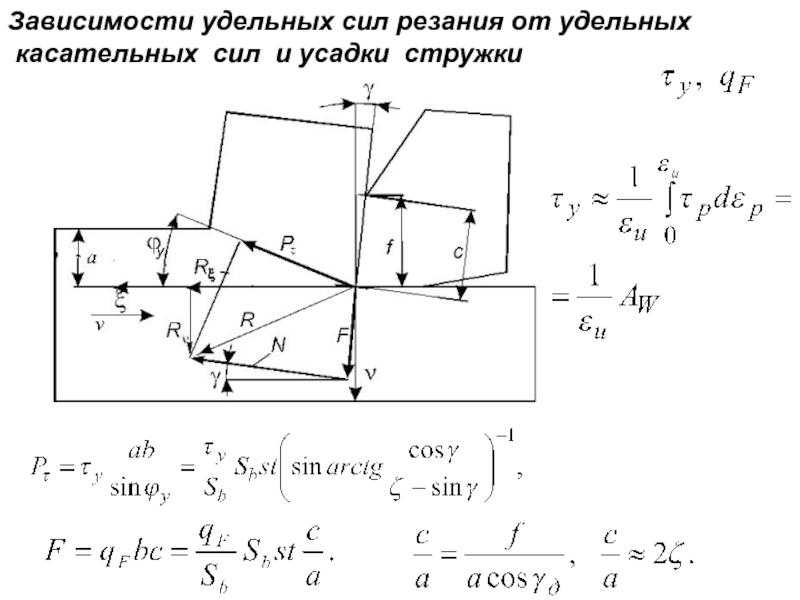

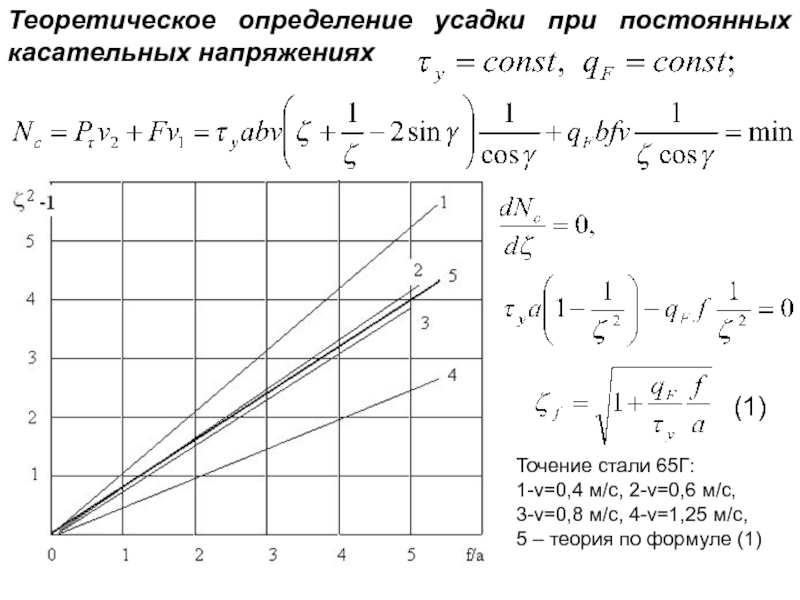
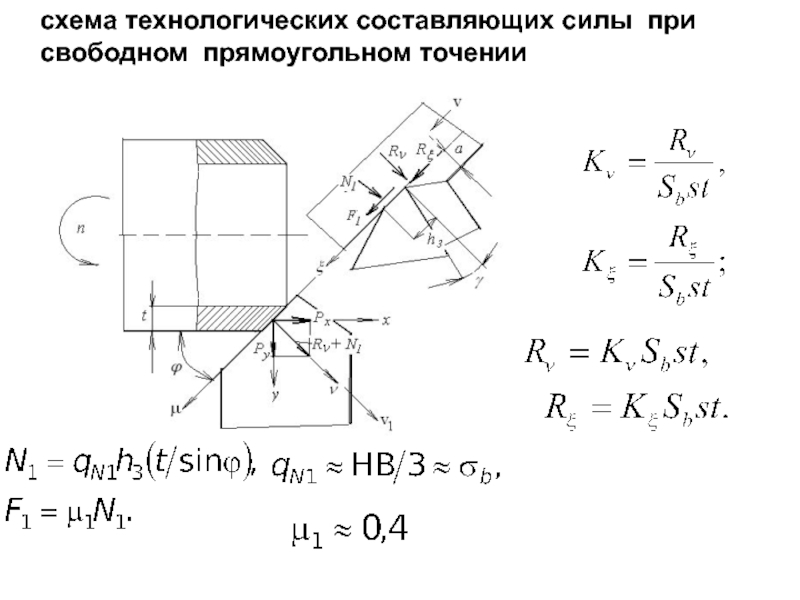
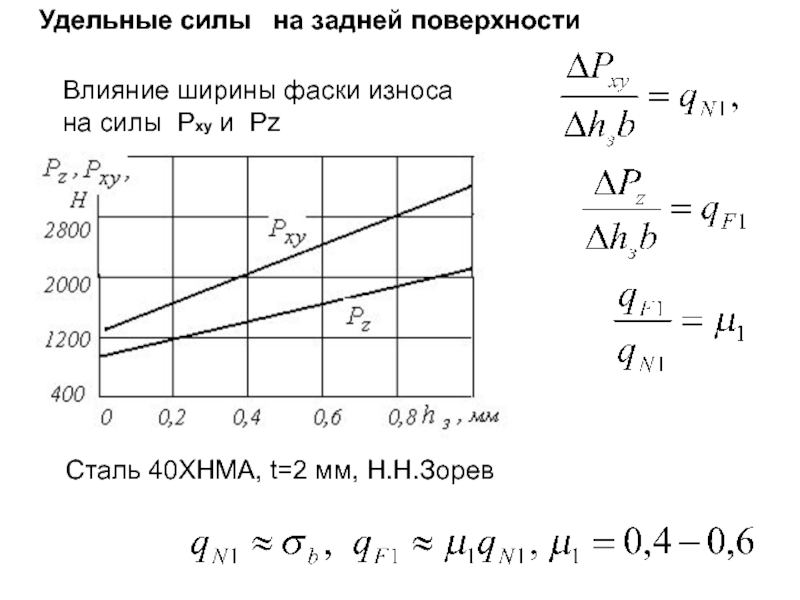

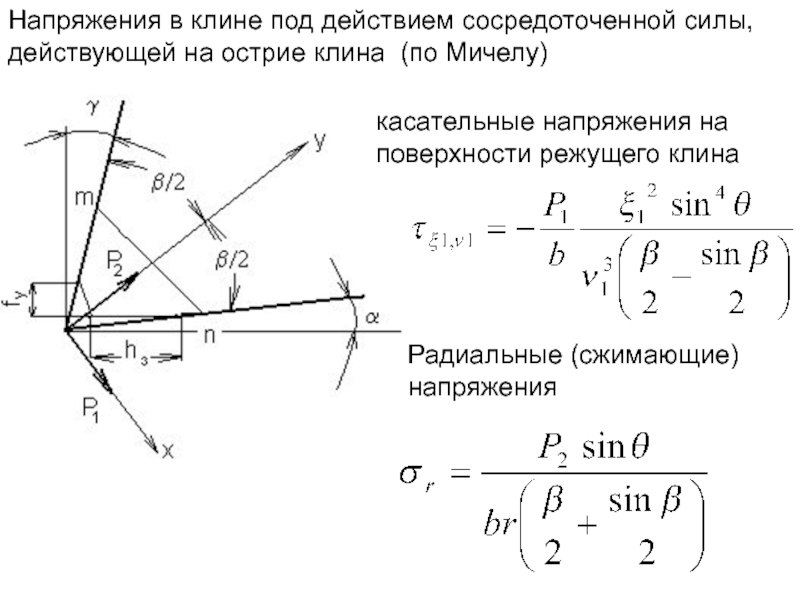
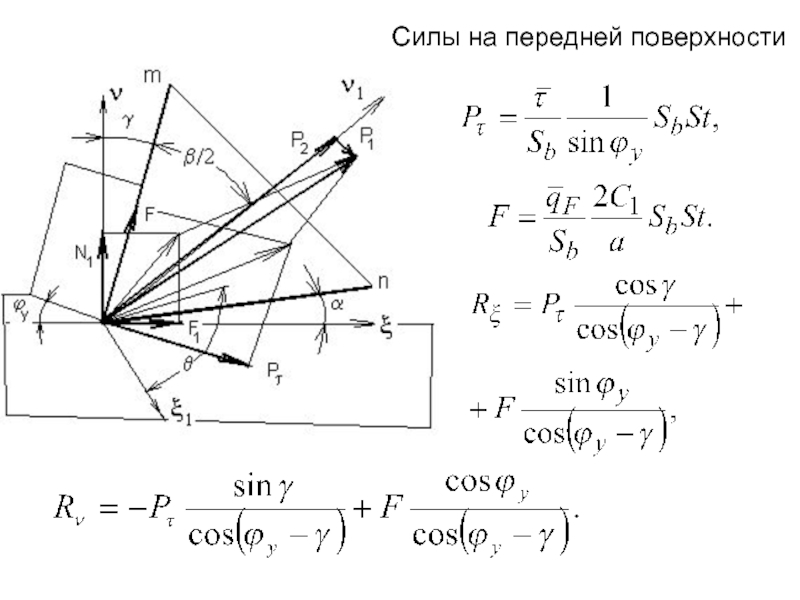
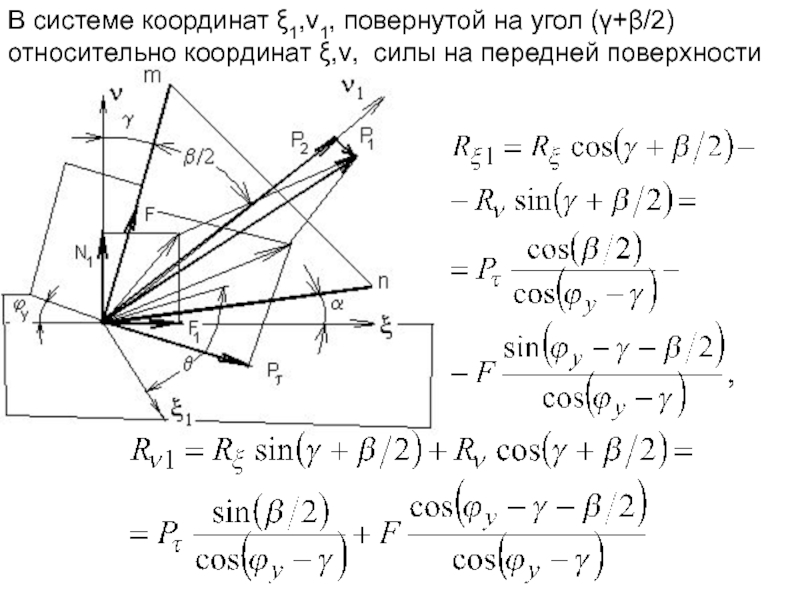



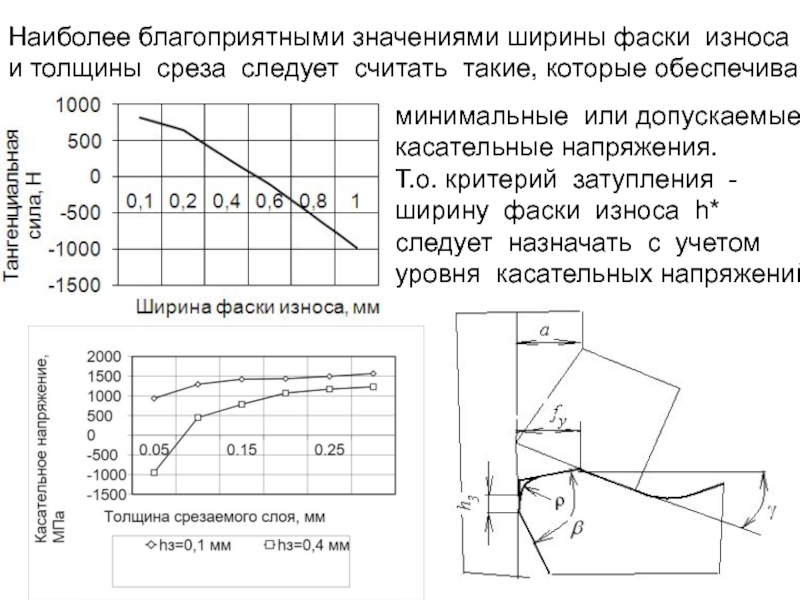
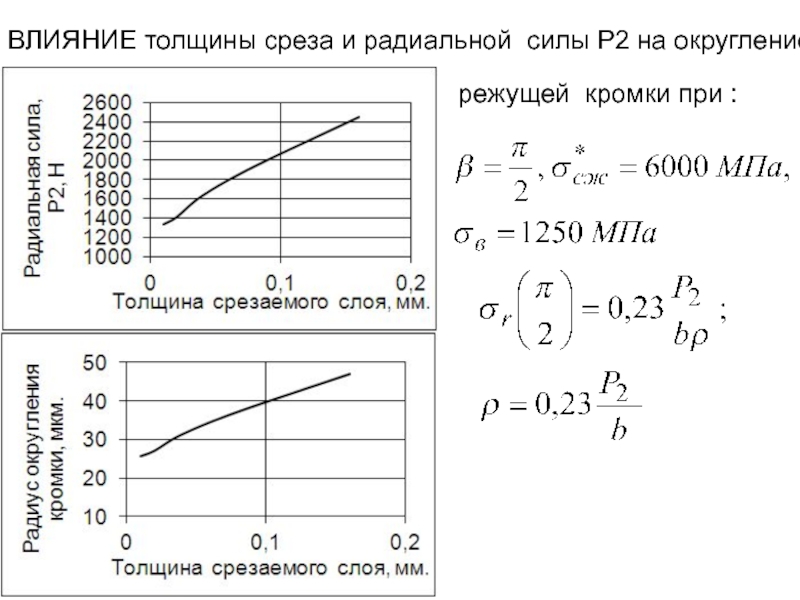






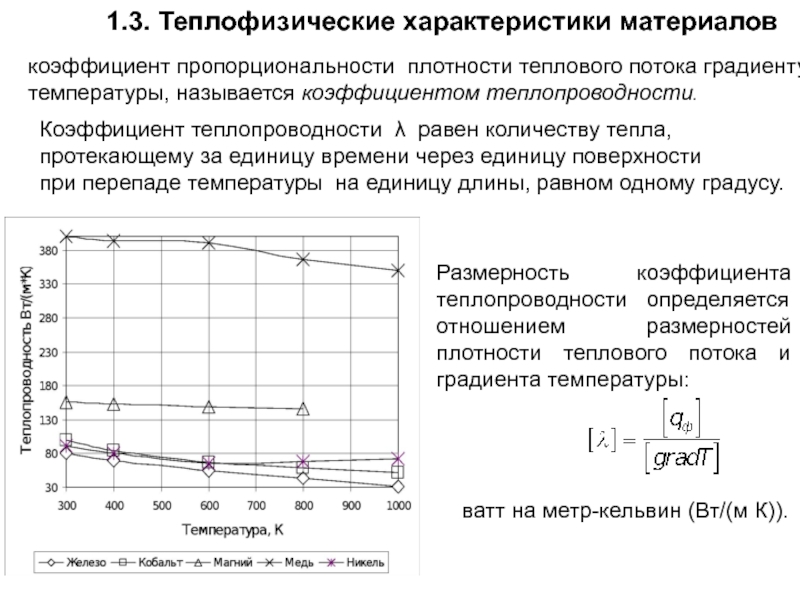

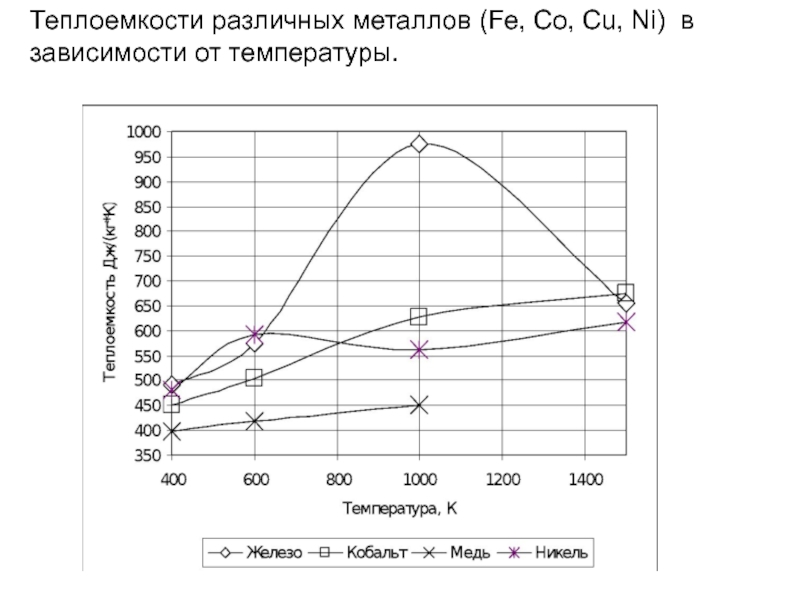
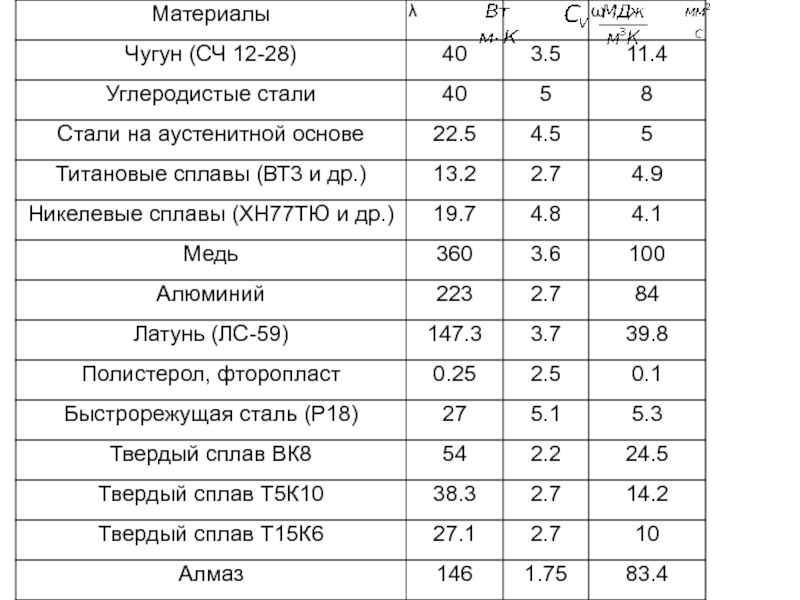
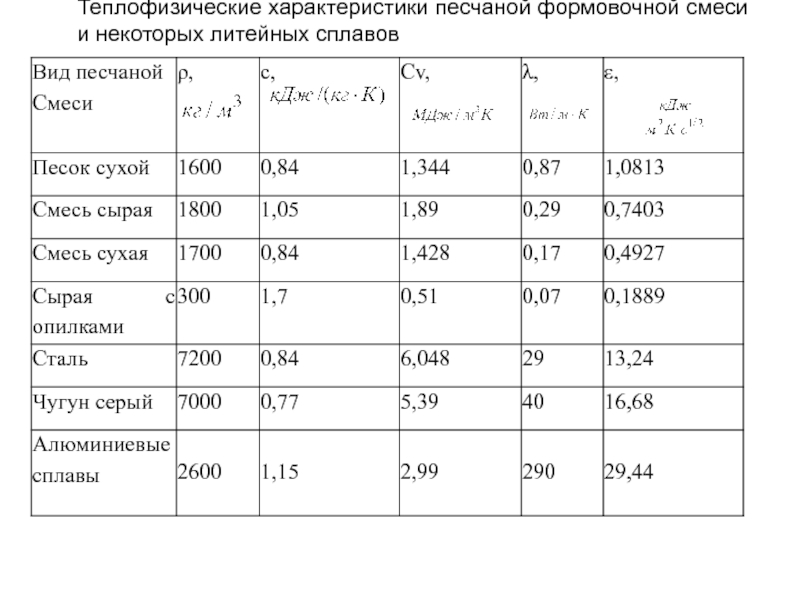

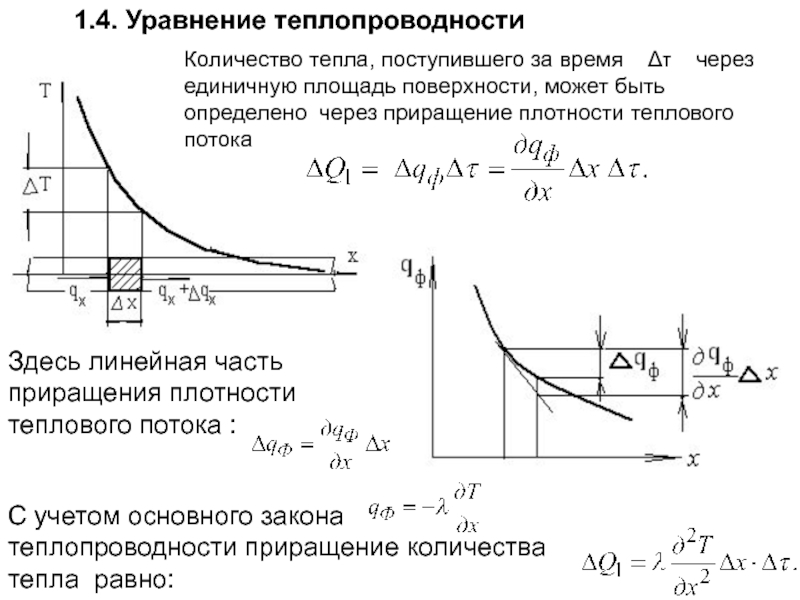




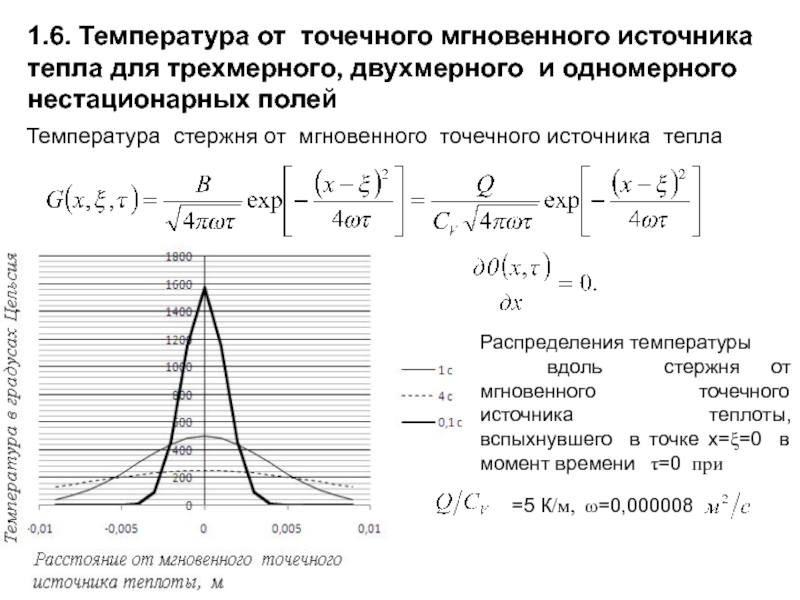








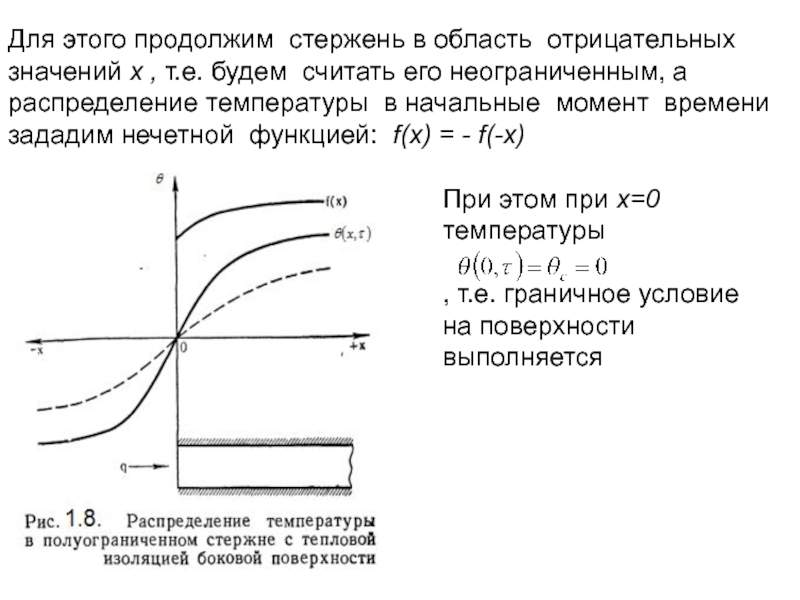



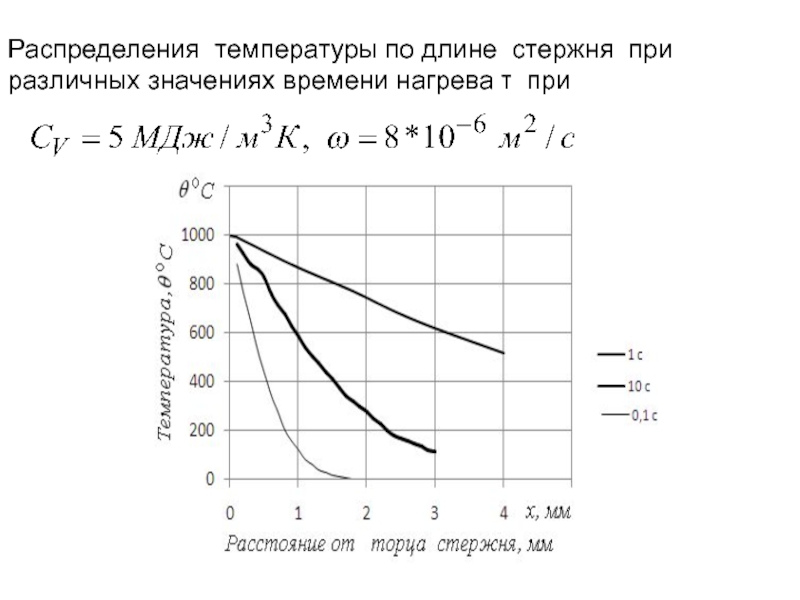
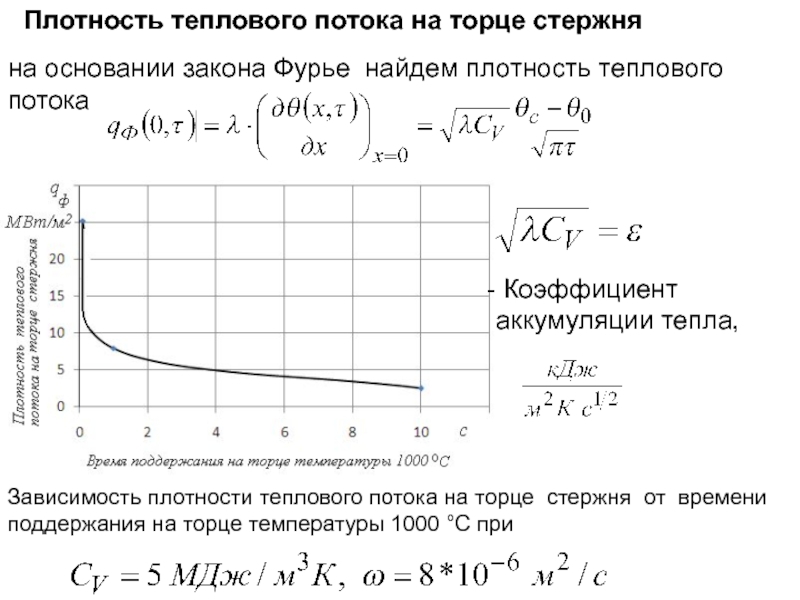
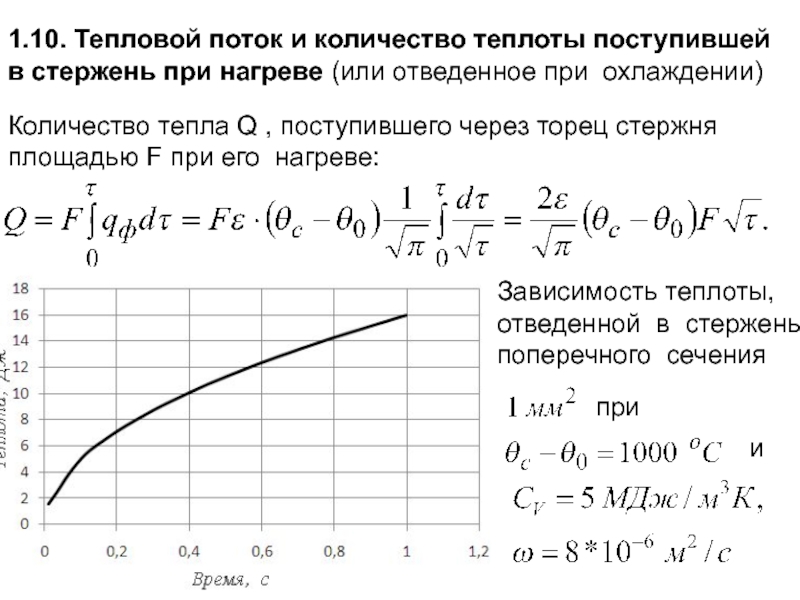
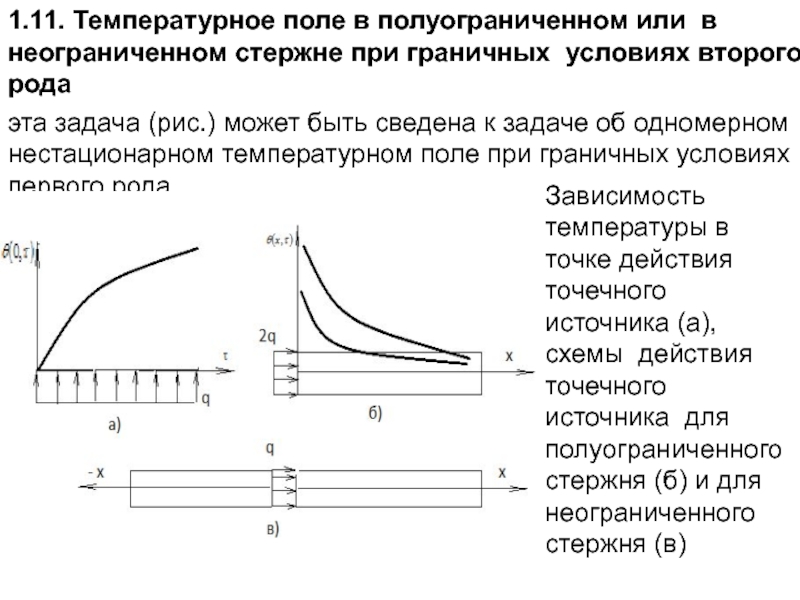






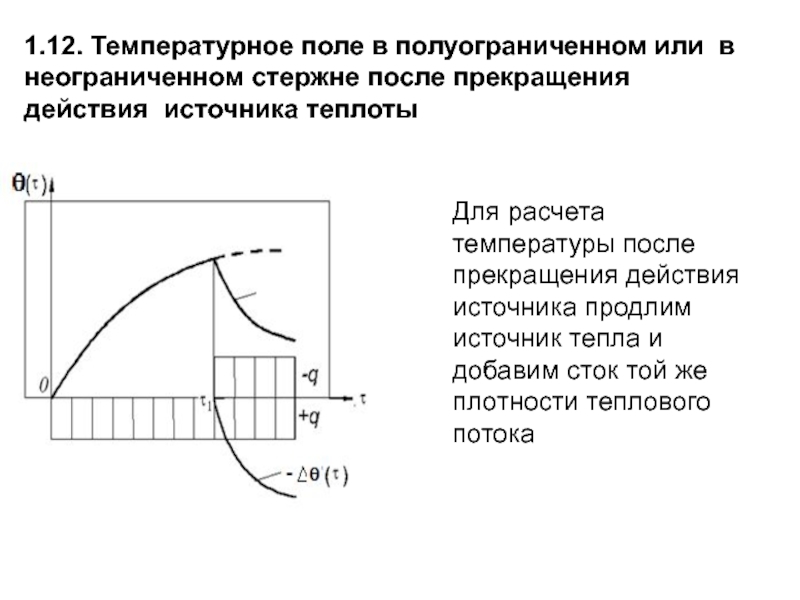

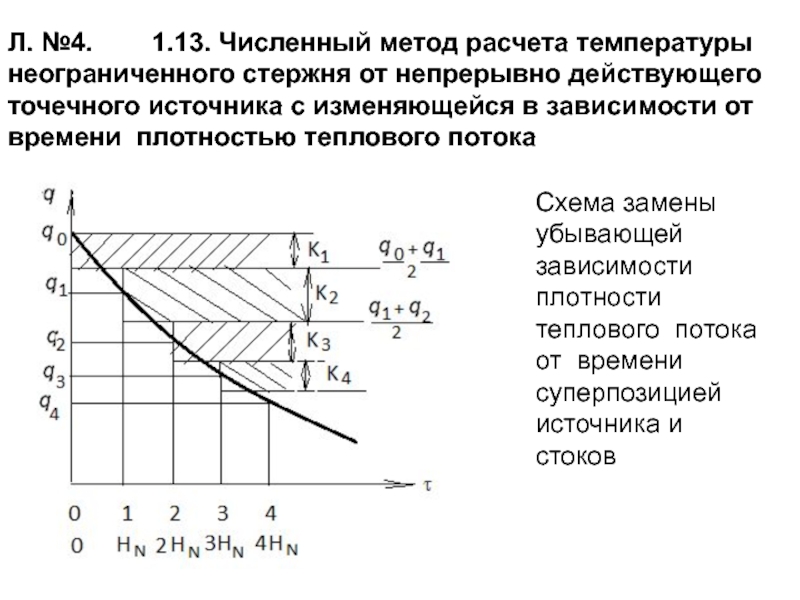
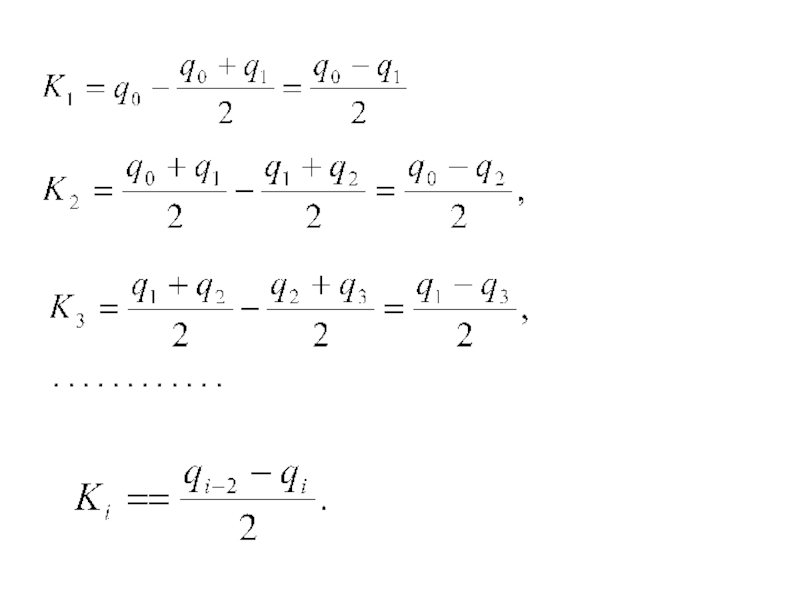


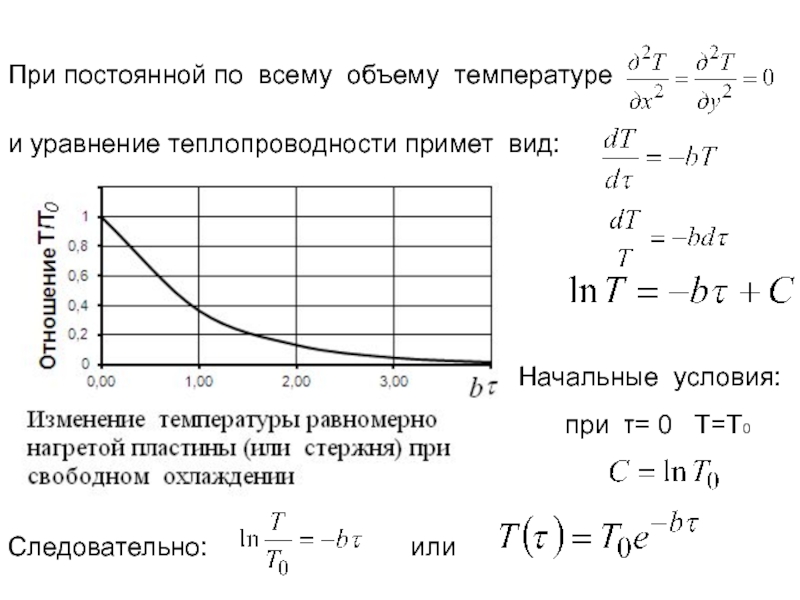
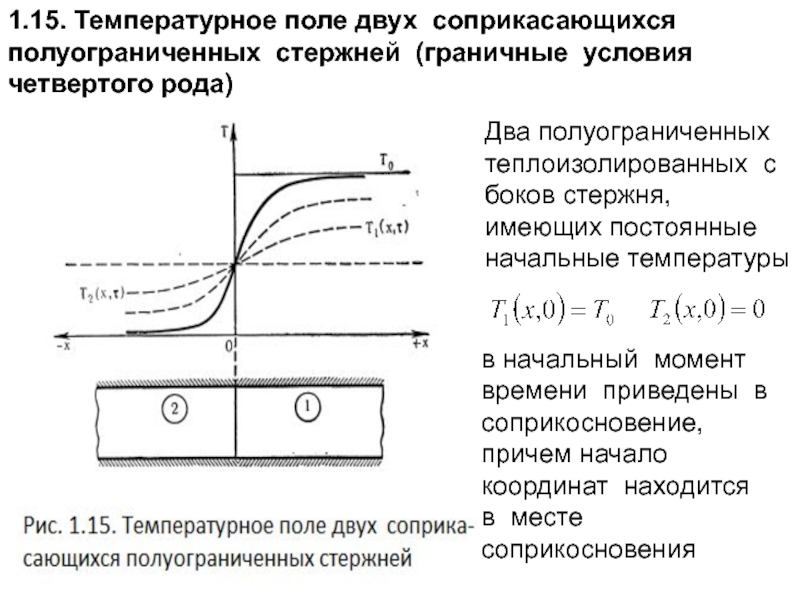






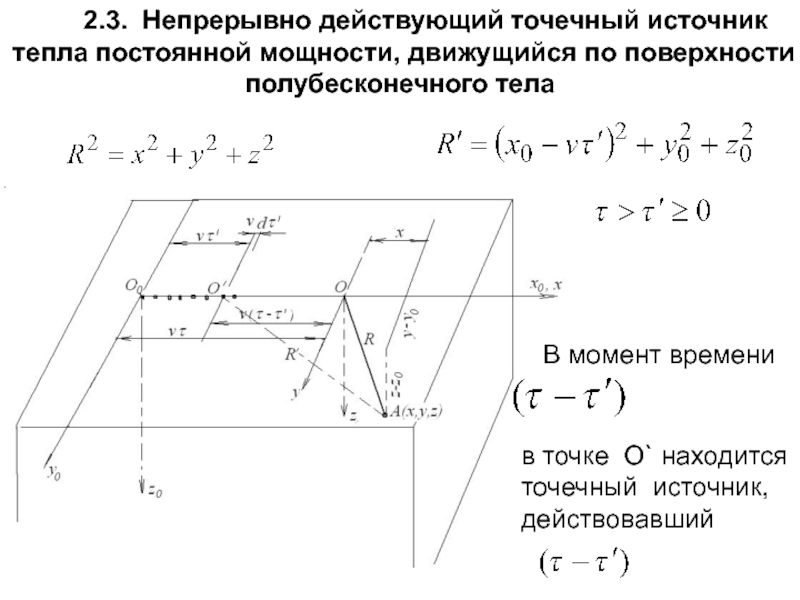




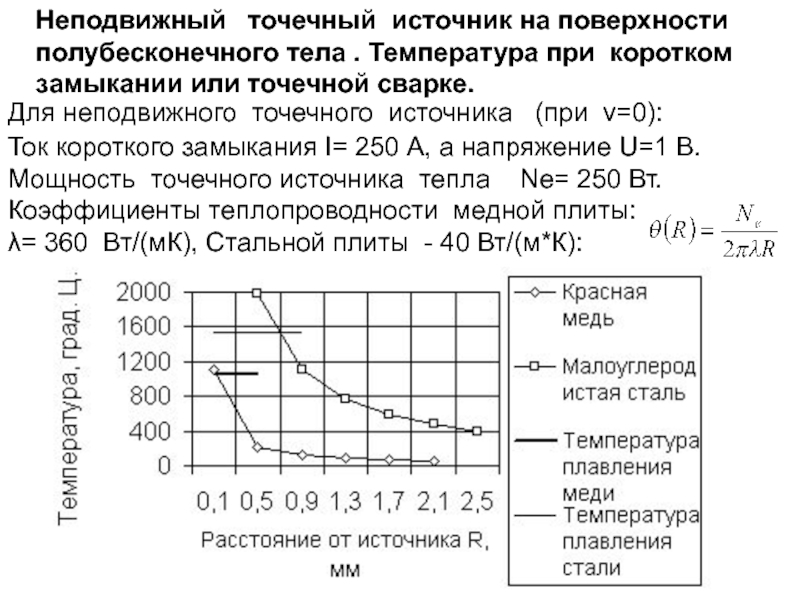

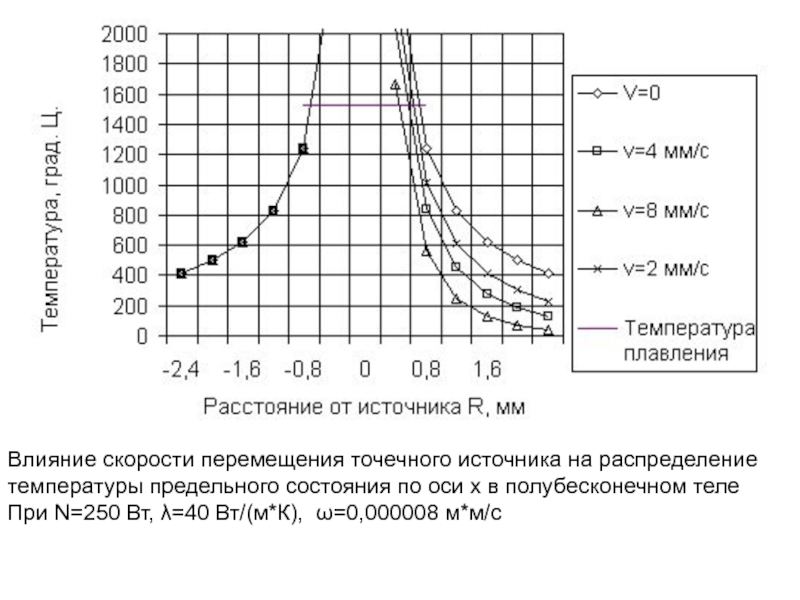
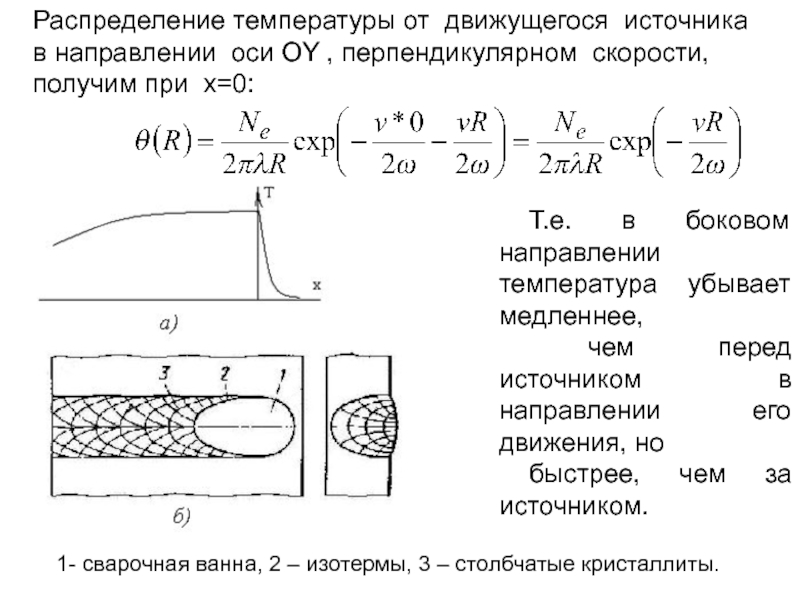



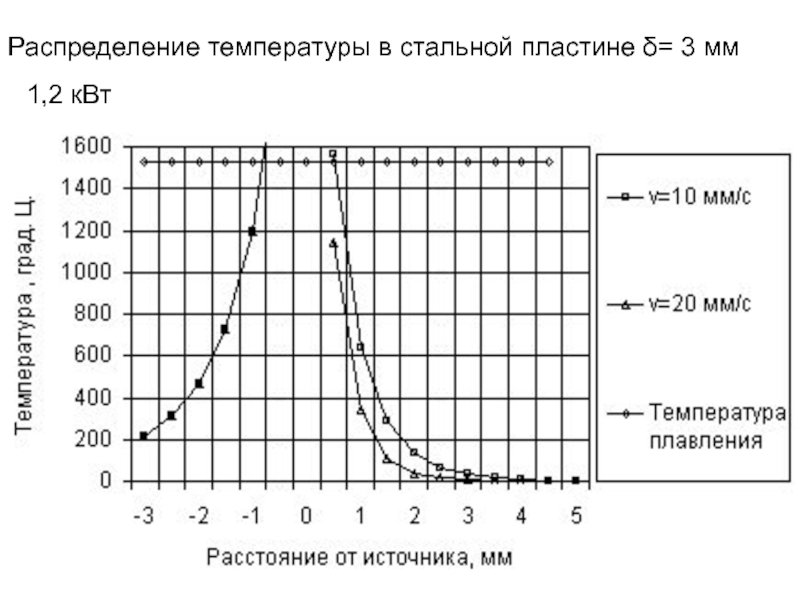
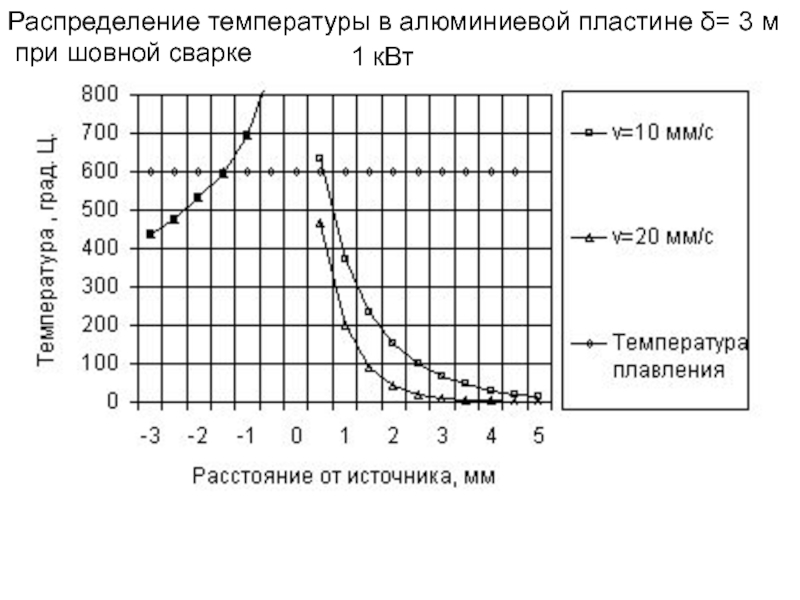
![Значения функции K(u) могут быть определены по таблицам [8]или графикам или численными методами. Для неподвижного](/img/tmb/5/430656/6d18c1610e3149ff4f8bdcbaaf4835e5-800x.jpg)
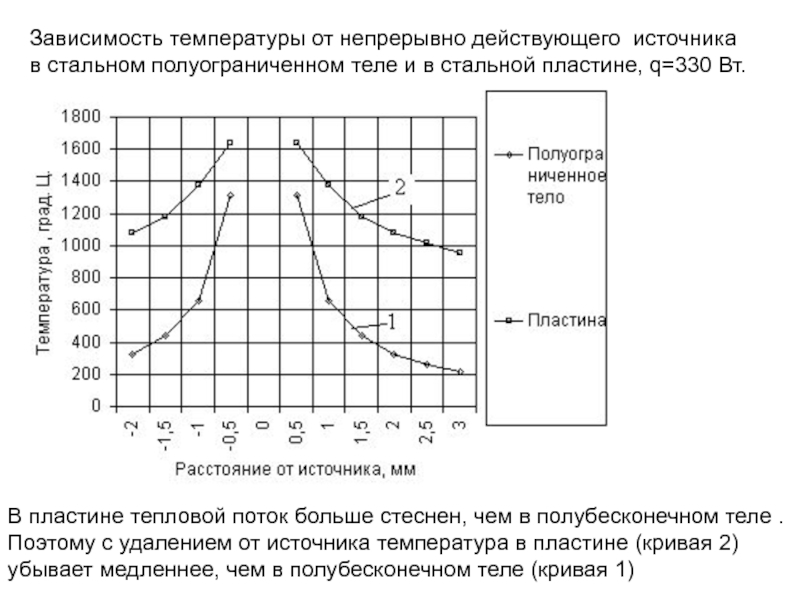

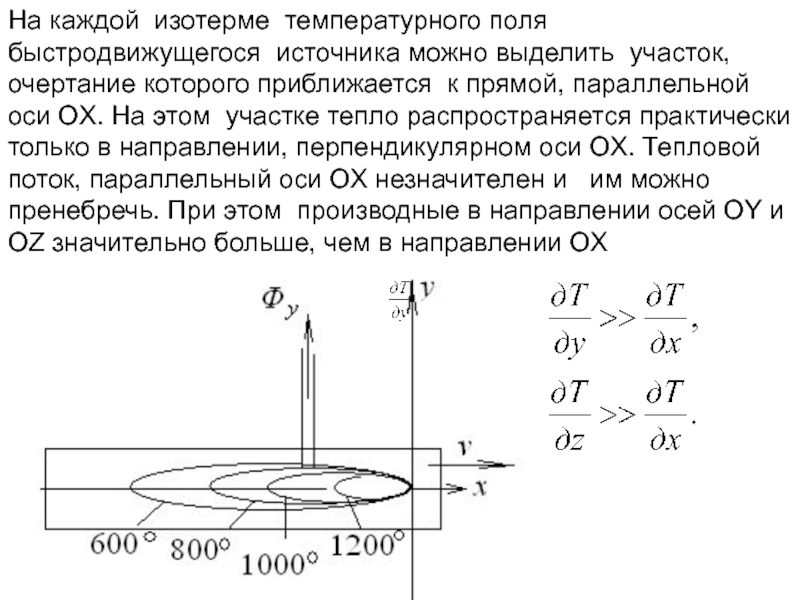
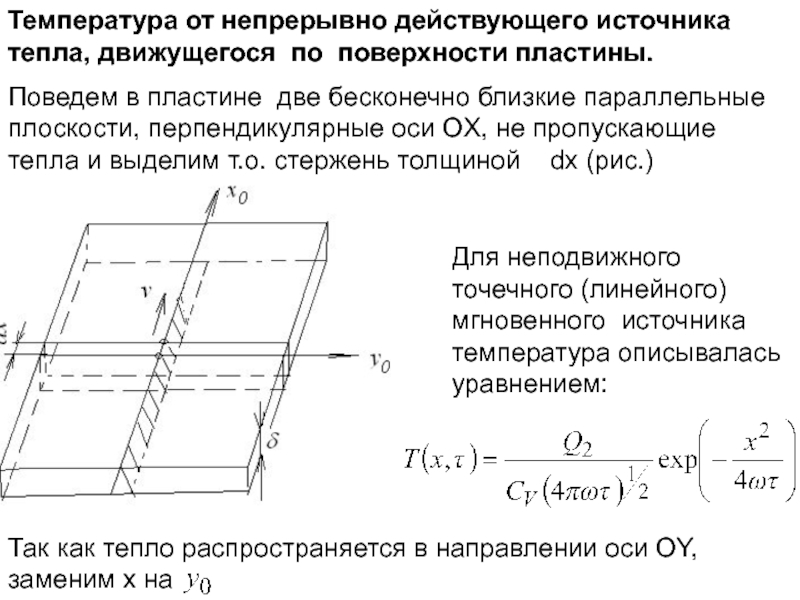

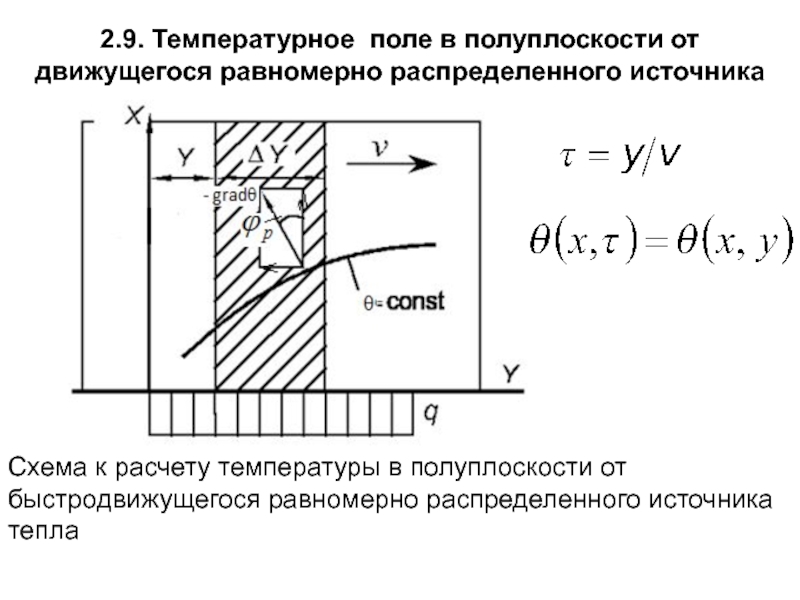

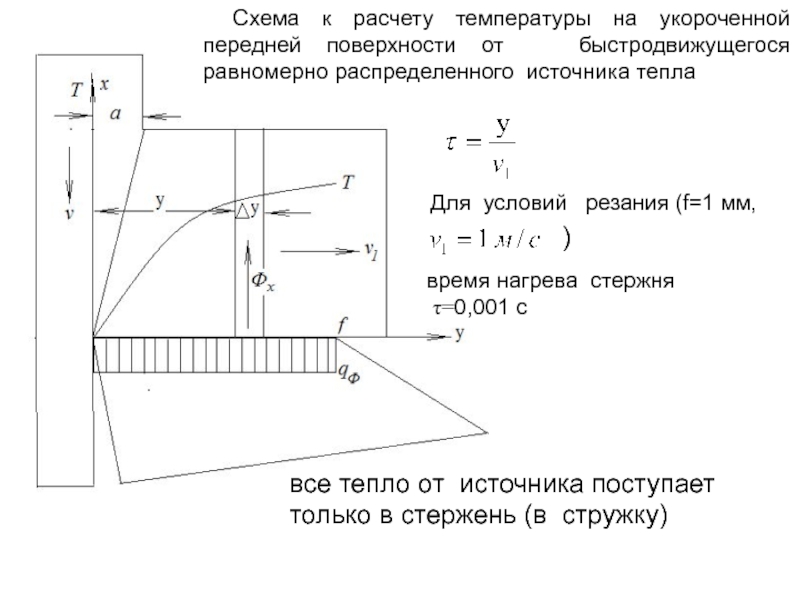

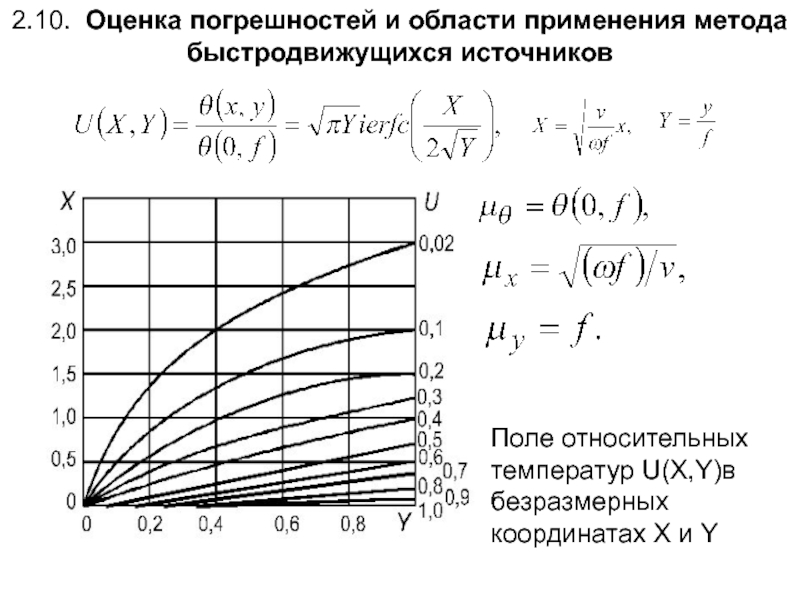
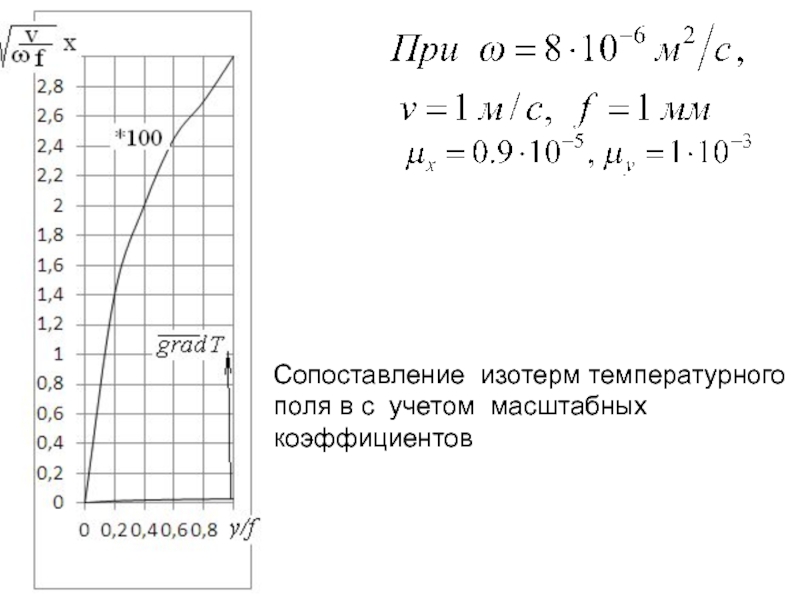

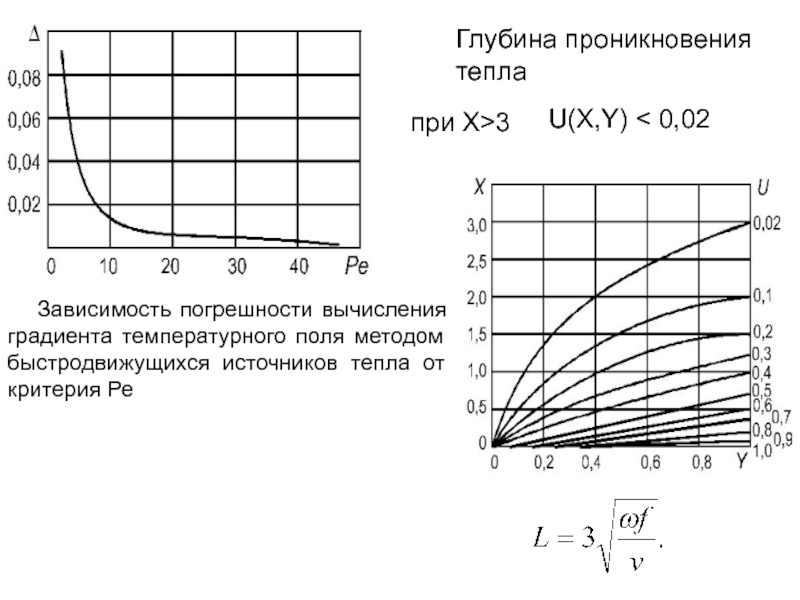

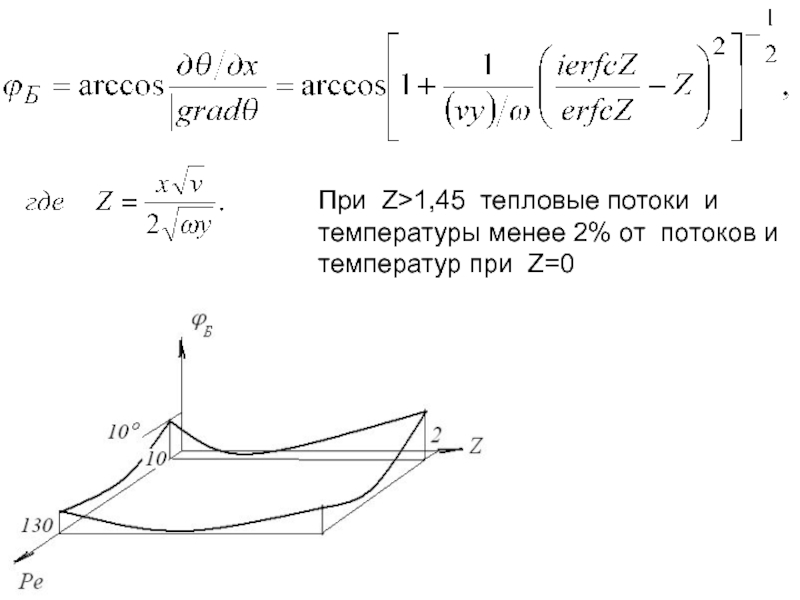

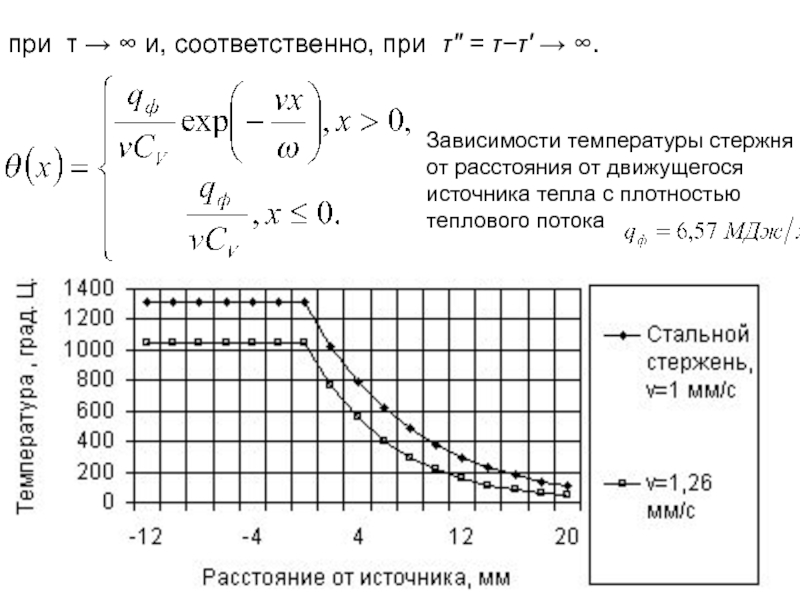
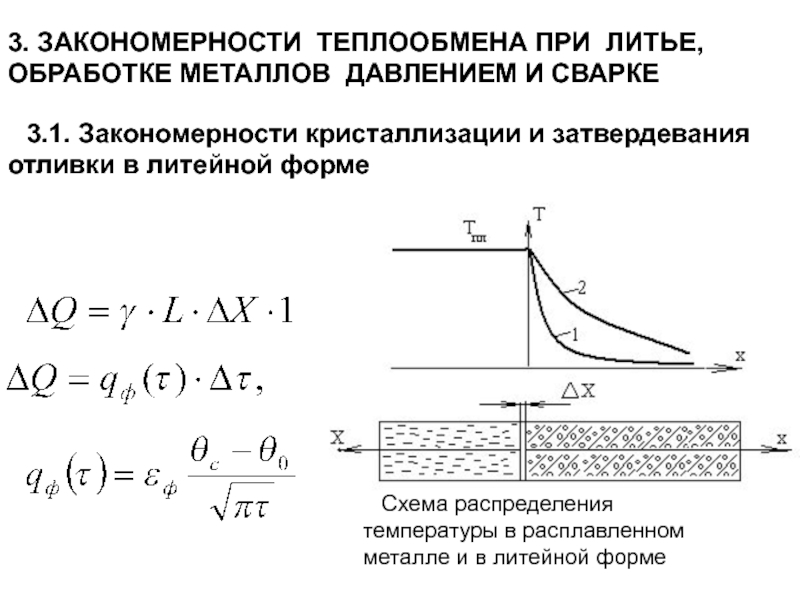

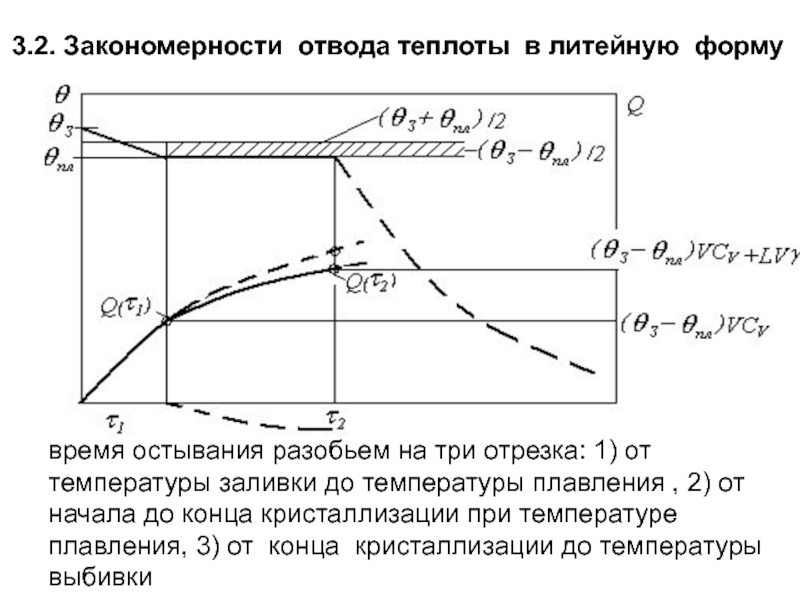


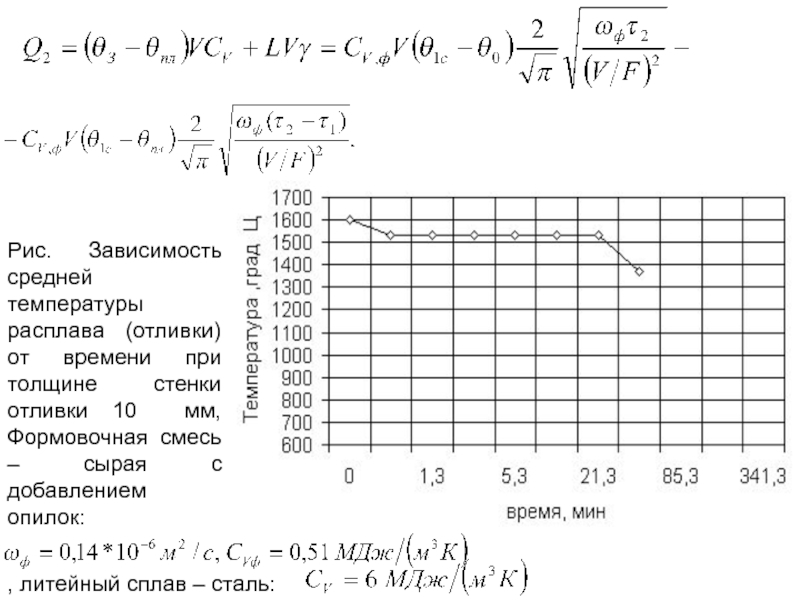
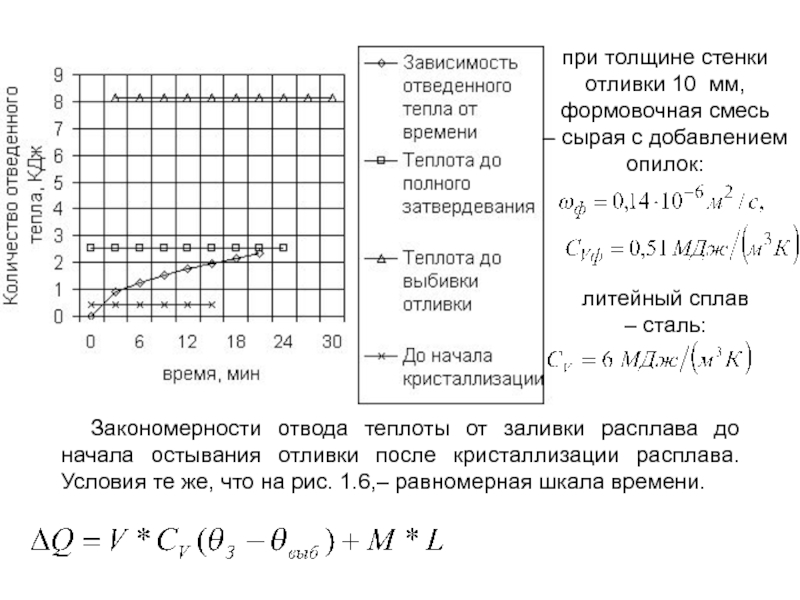
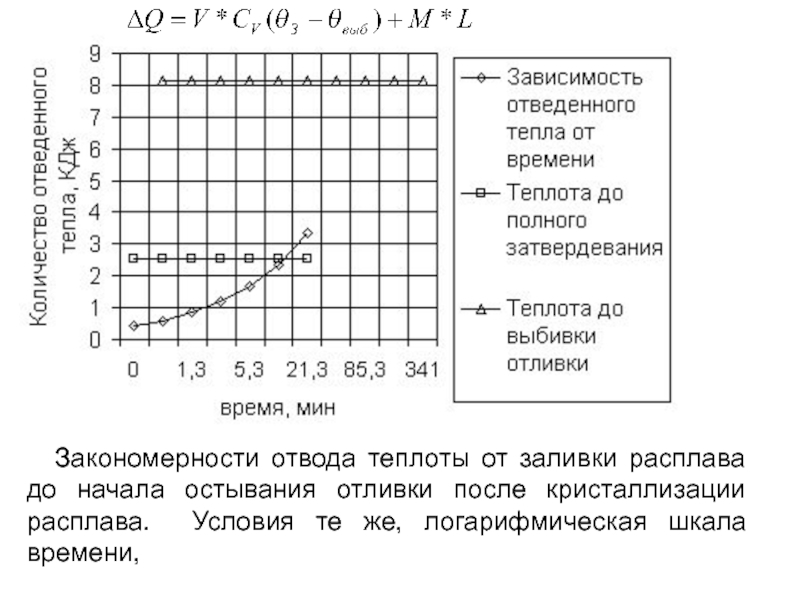
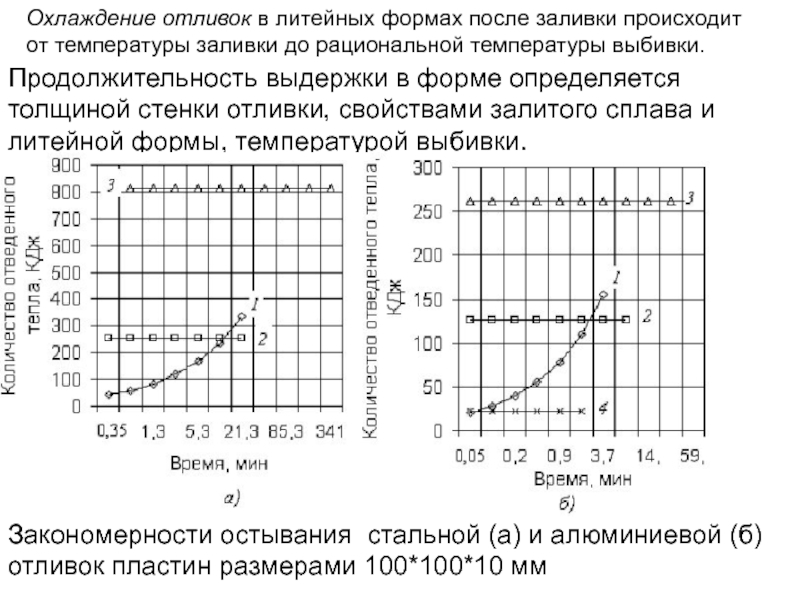
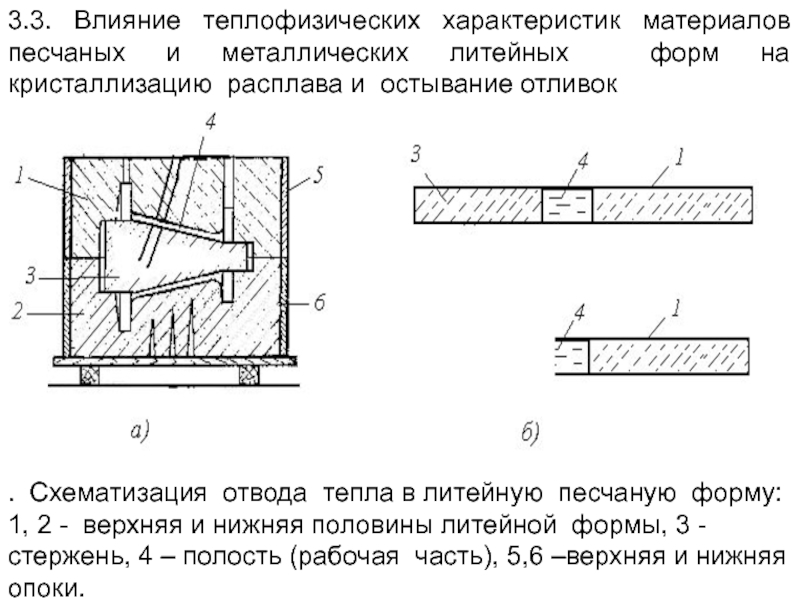
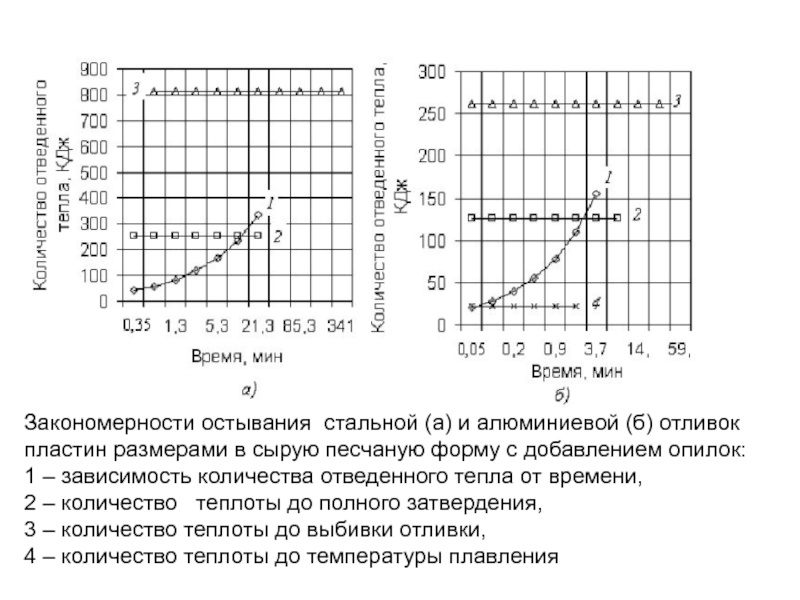
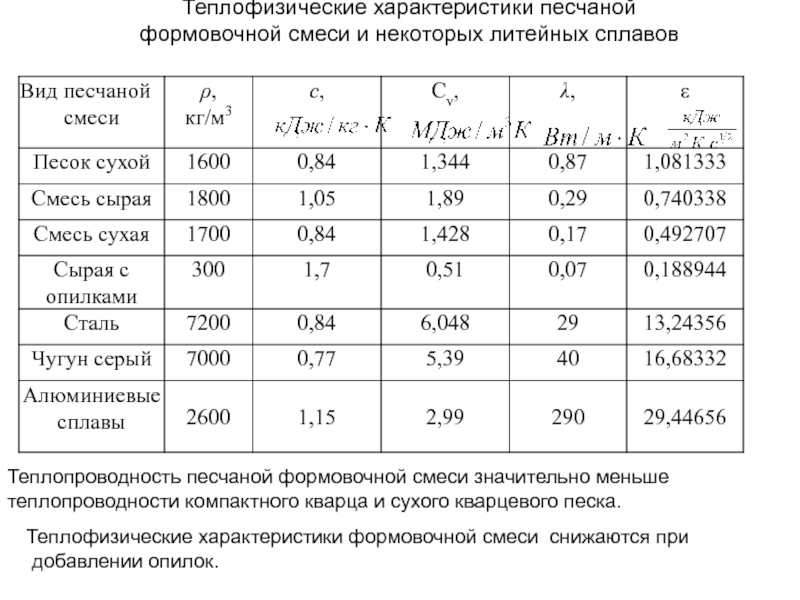
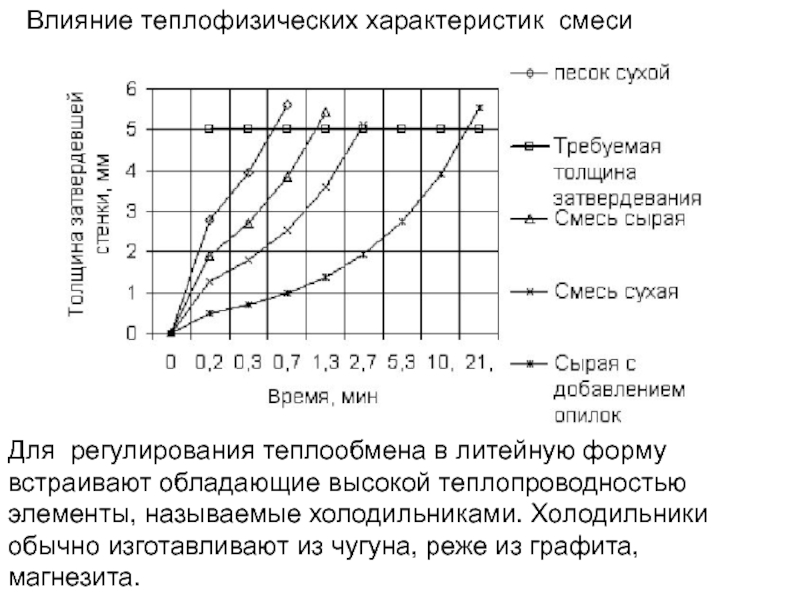
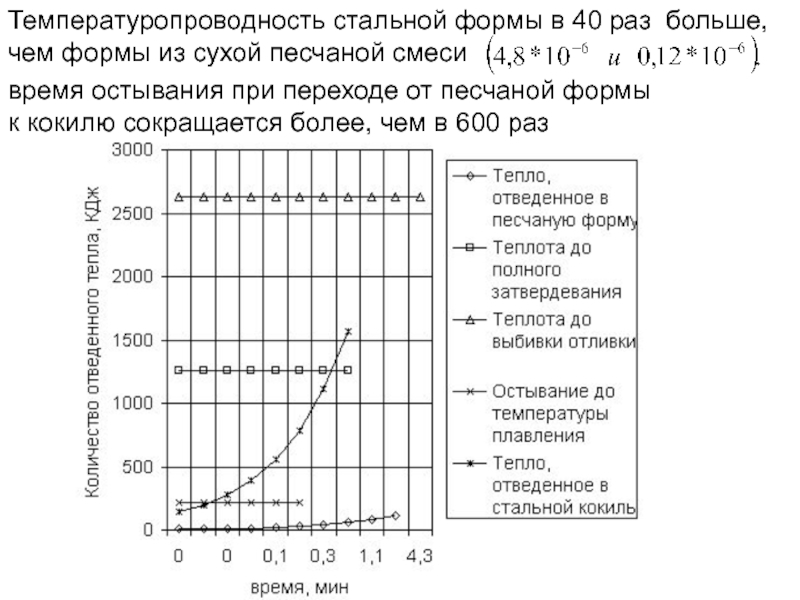
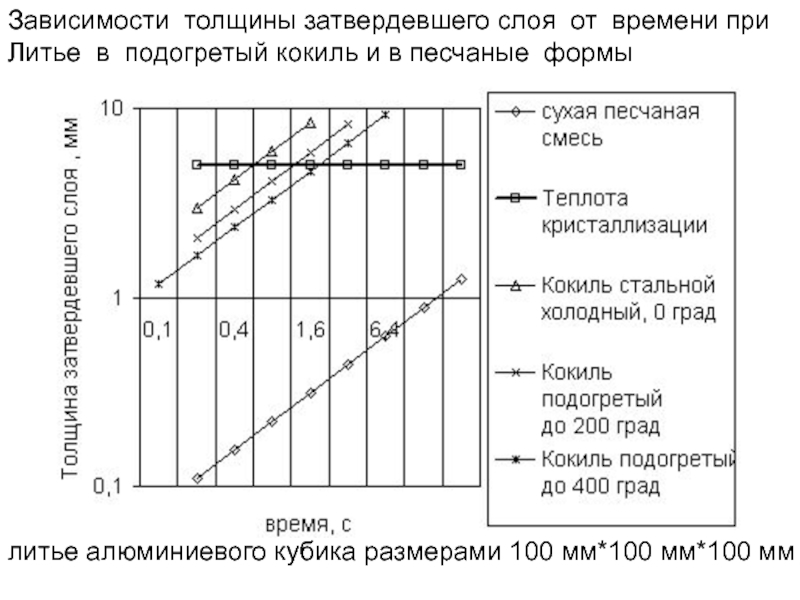
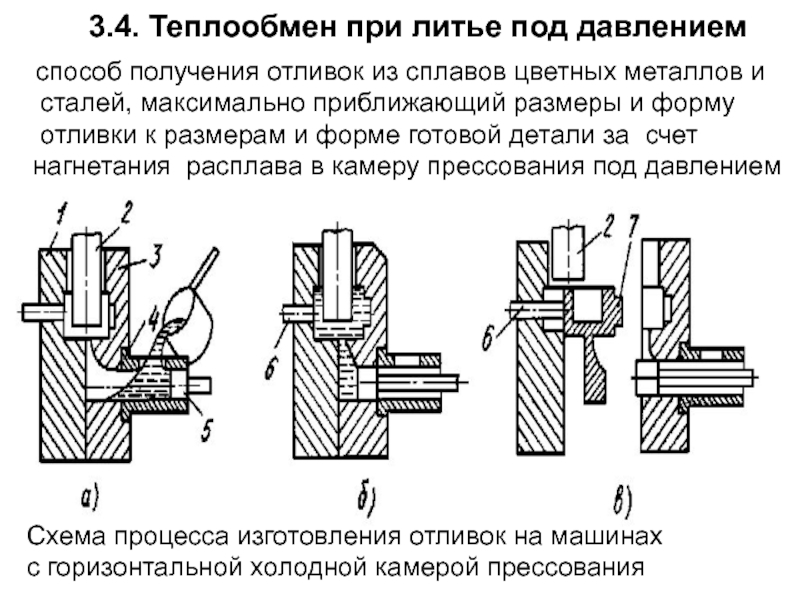
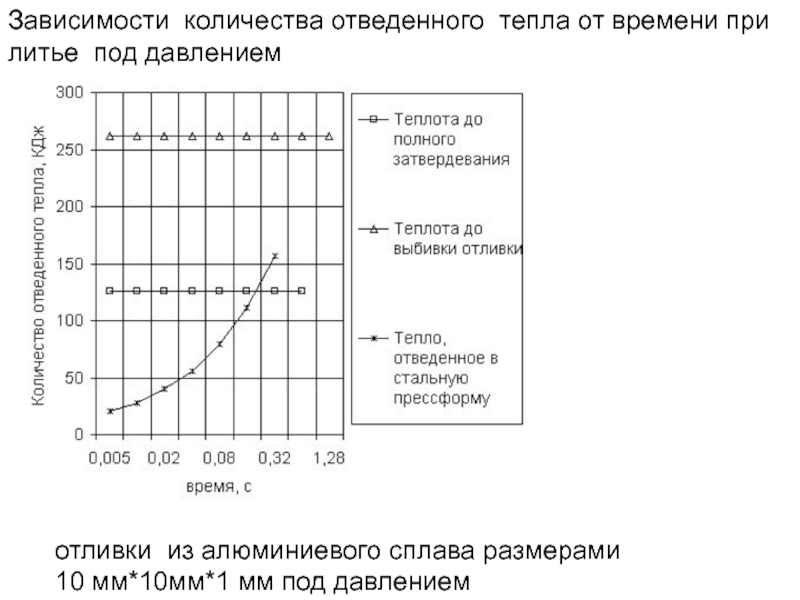
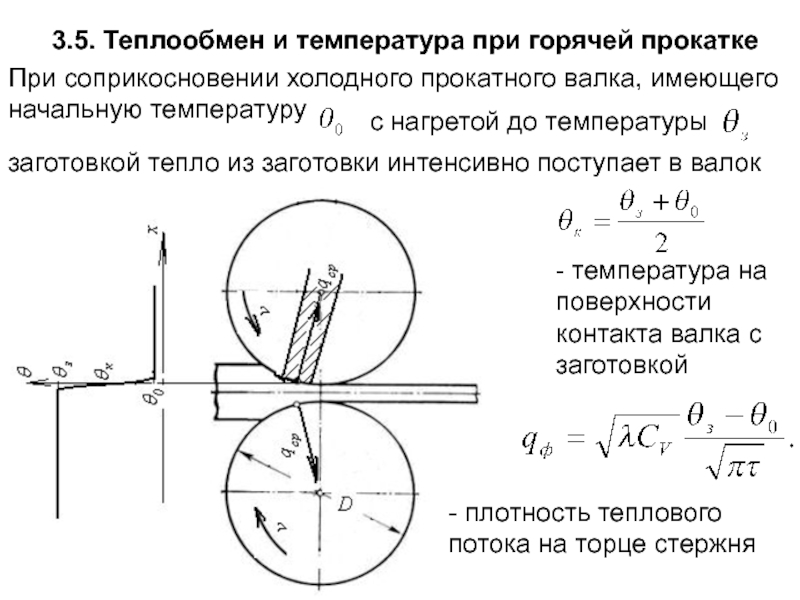


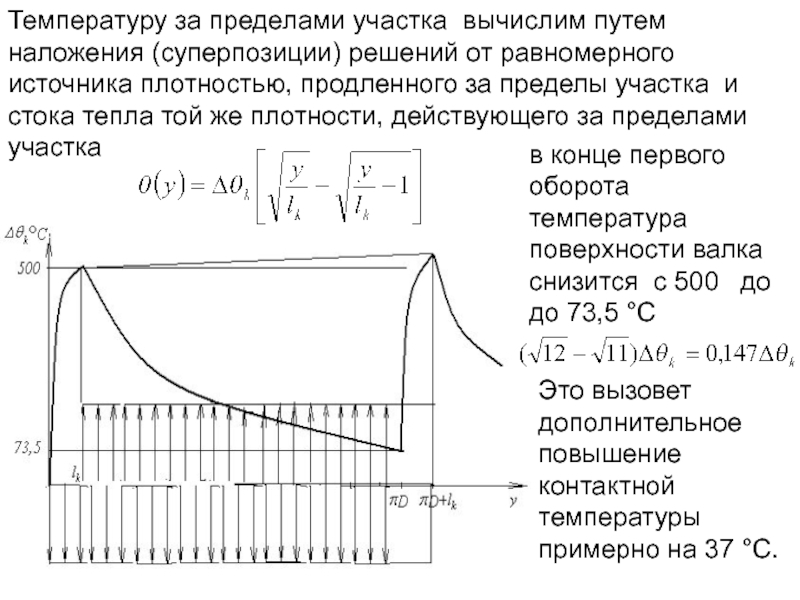

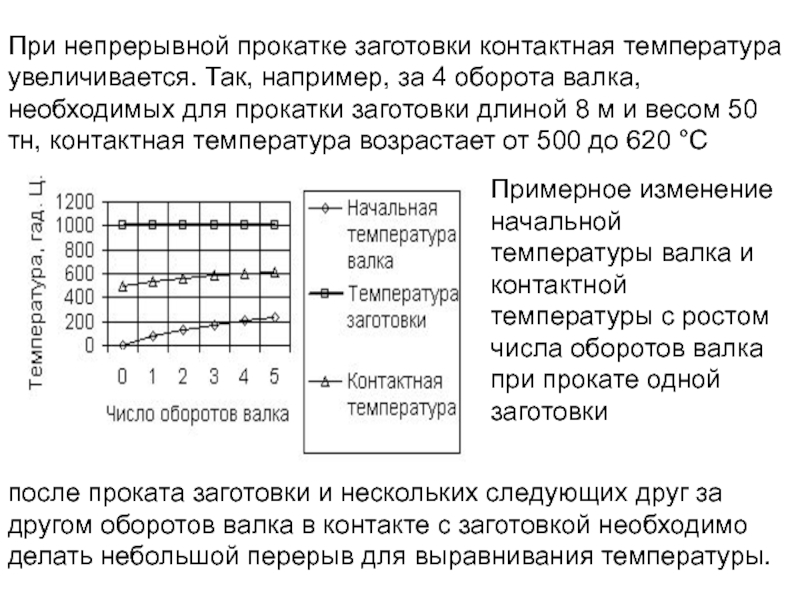
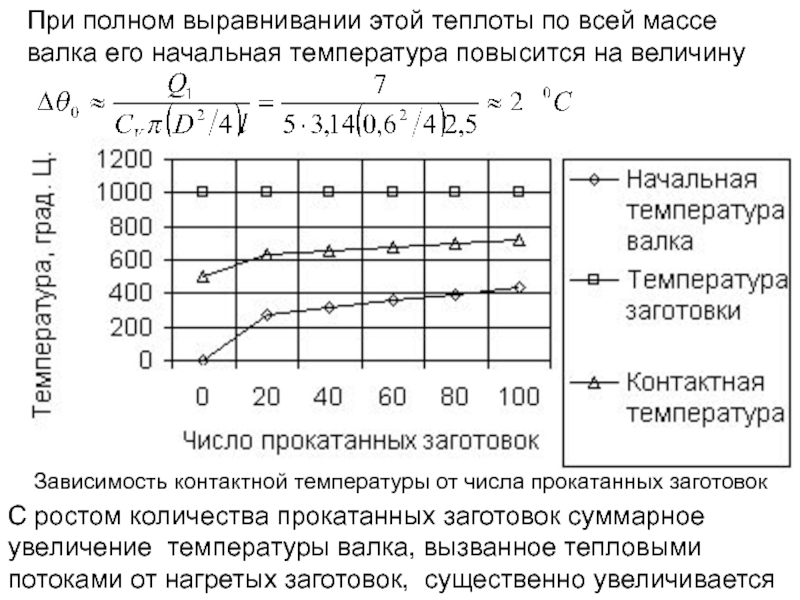
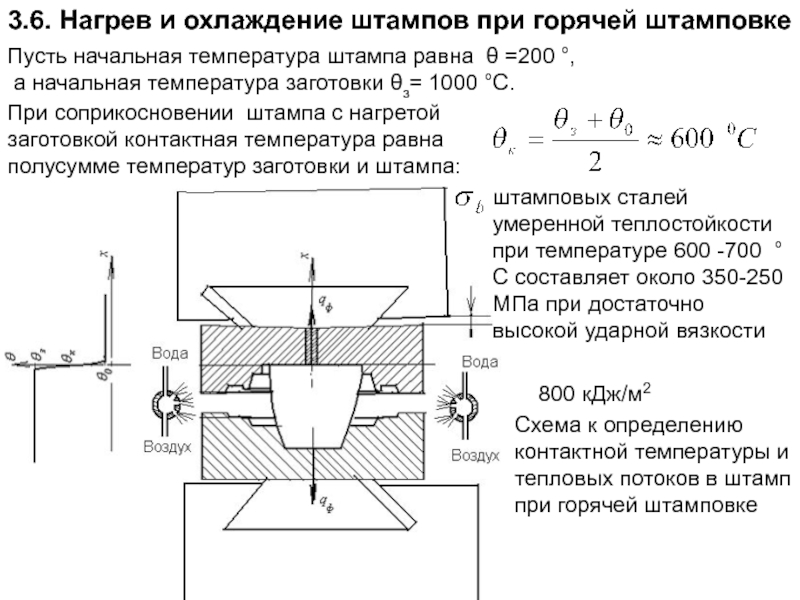
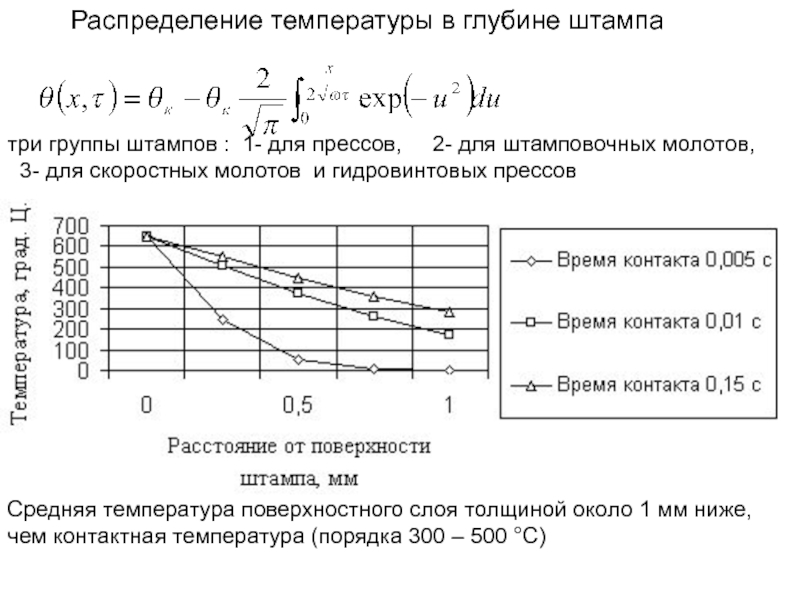
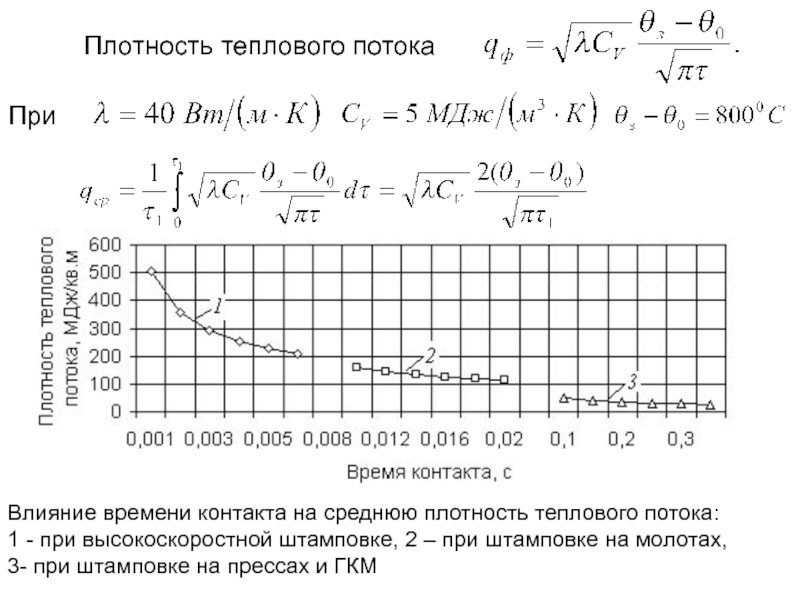
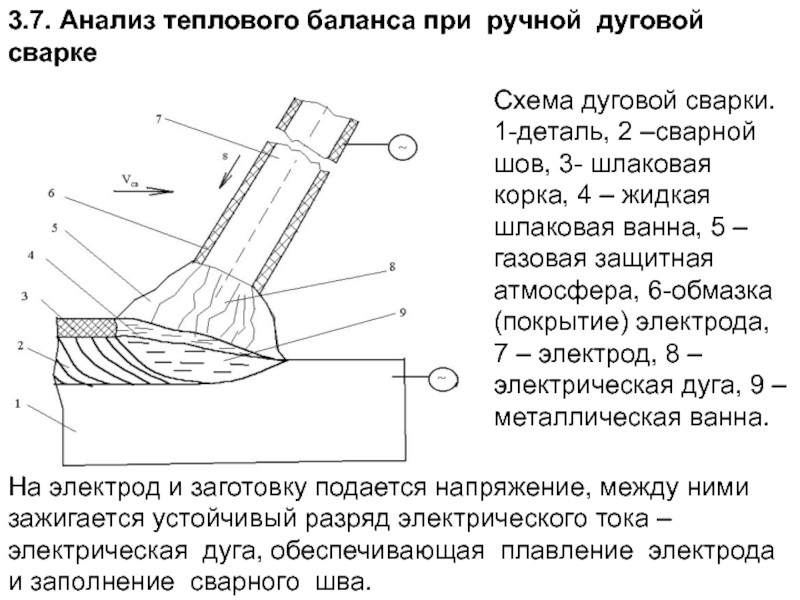
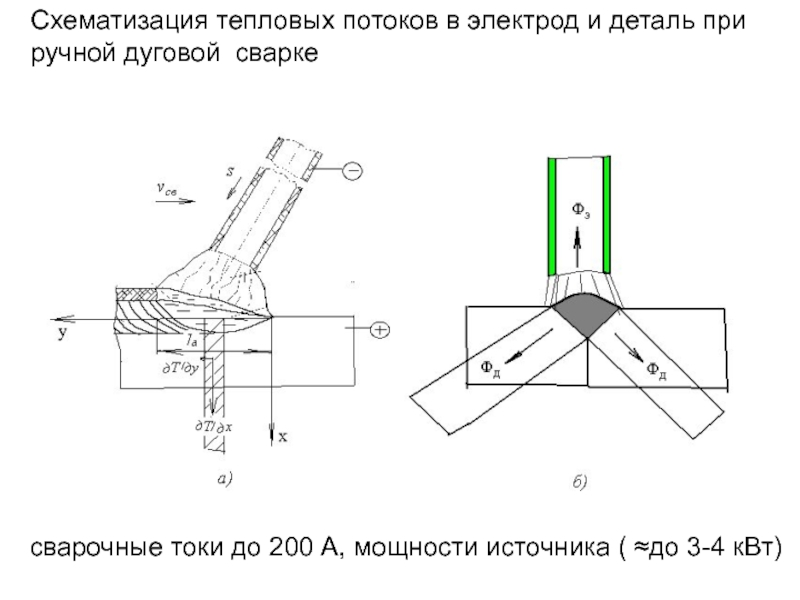
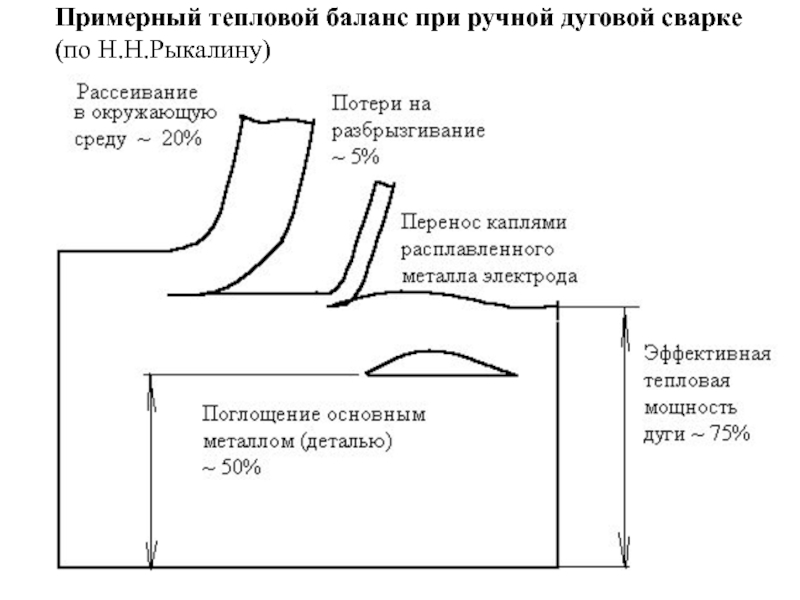



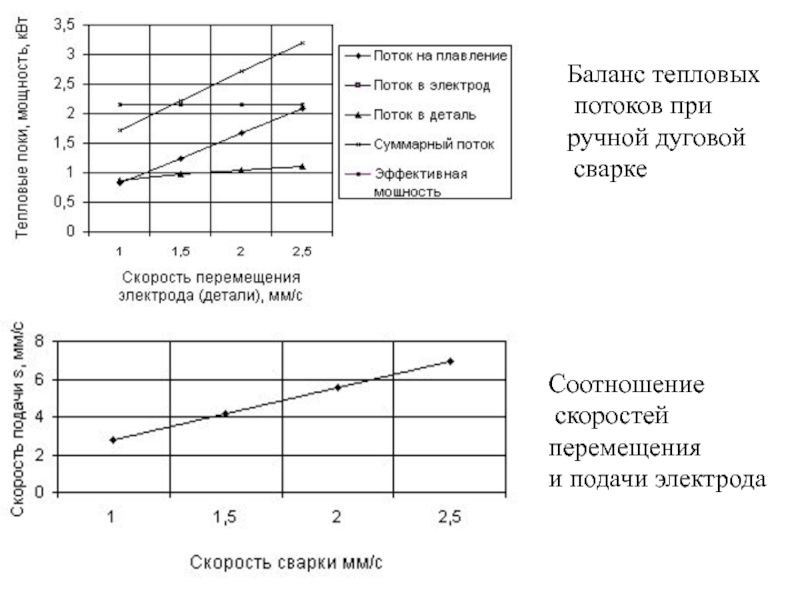
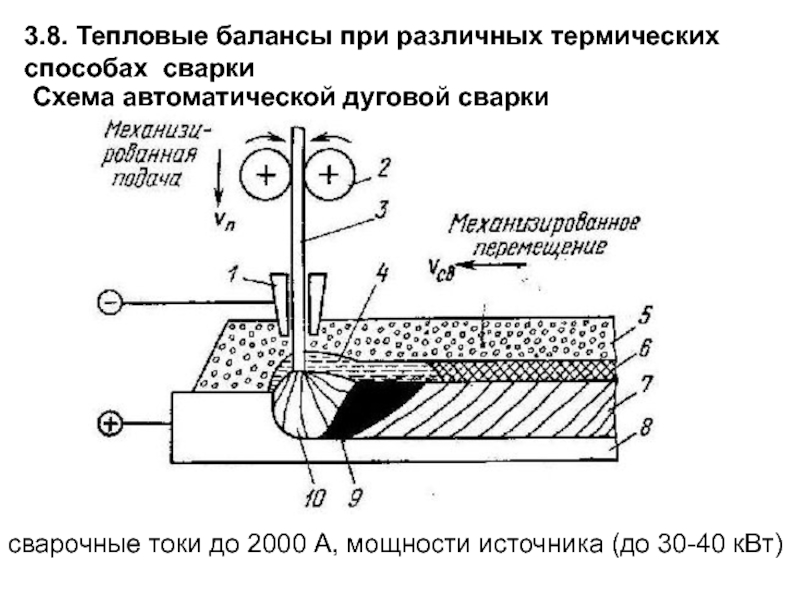
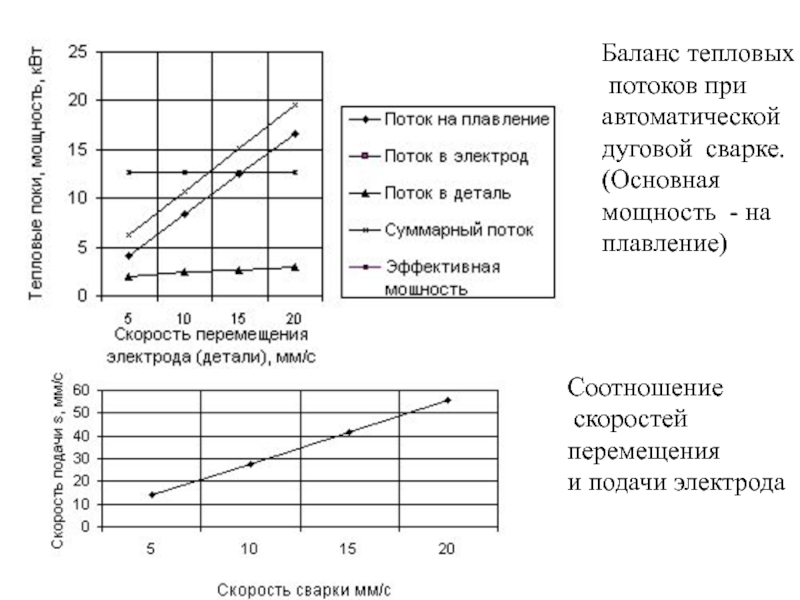
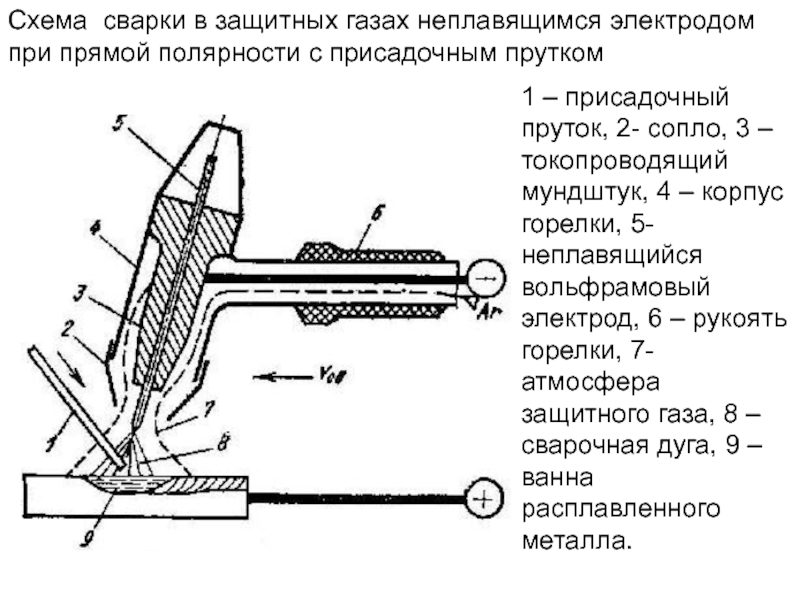
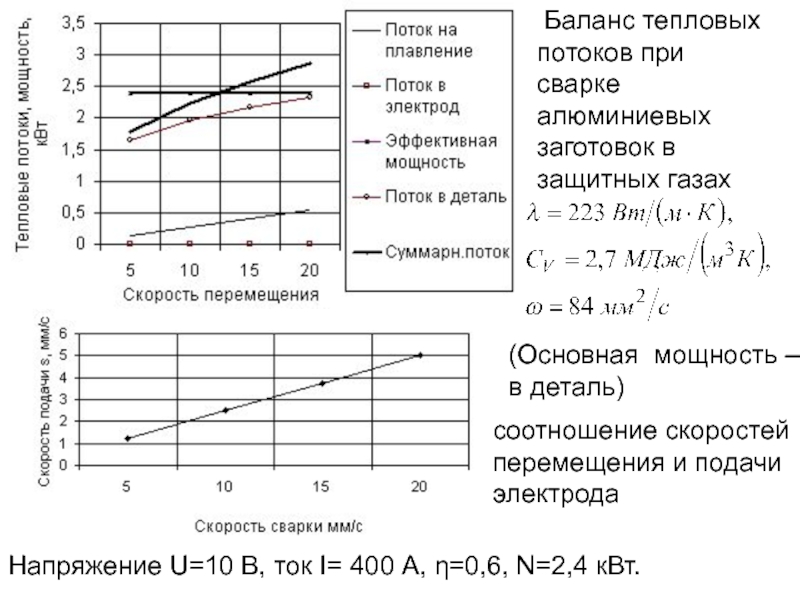
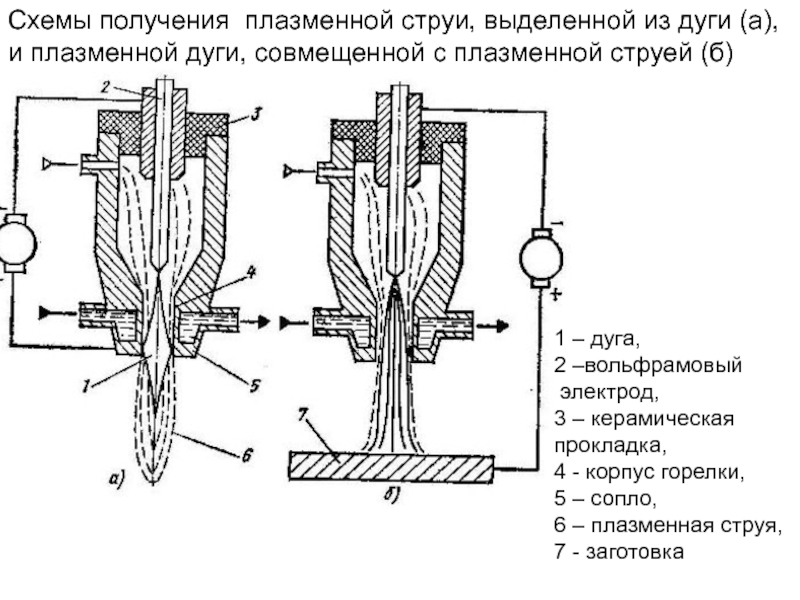
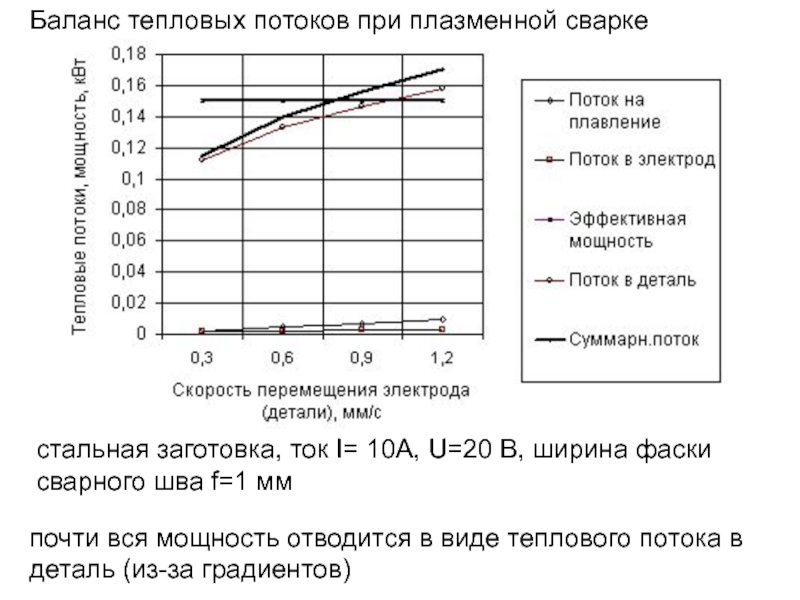
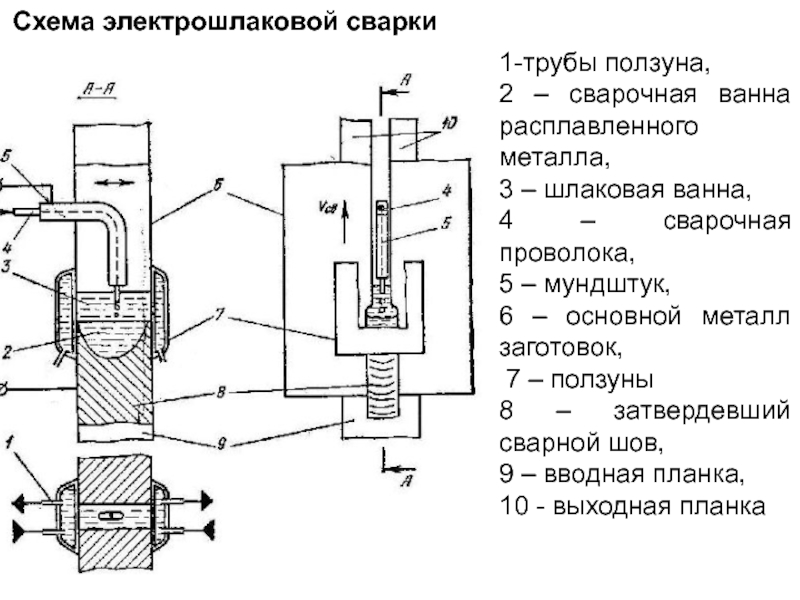
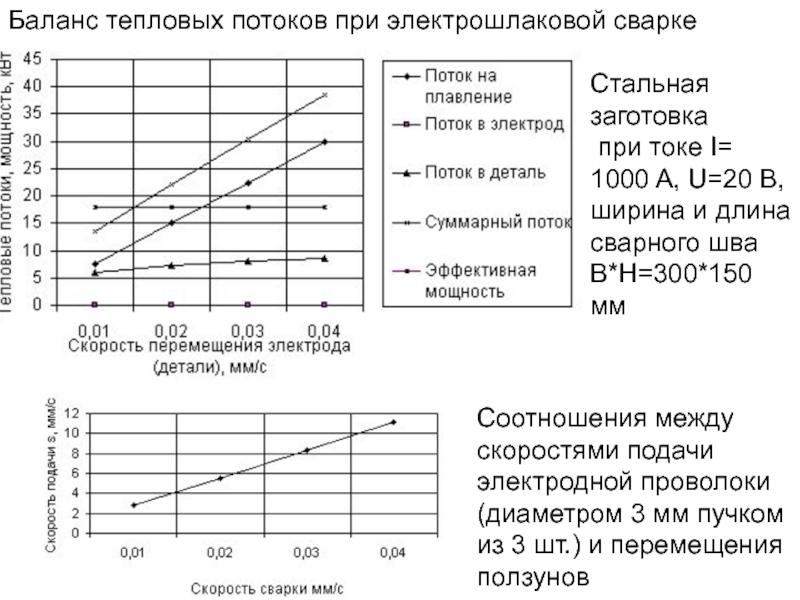
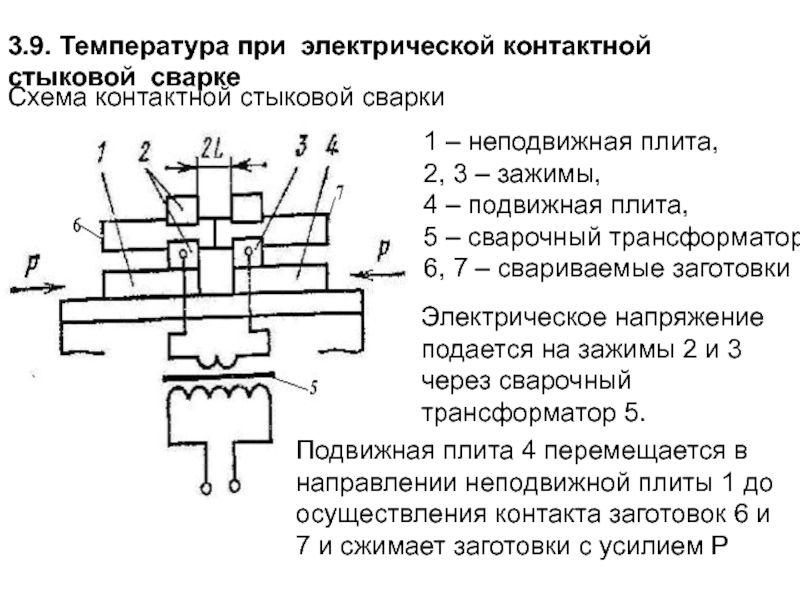
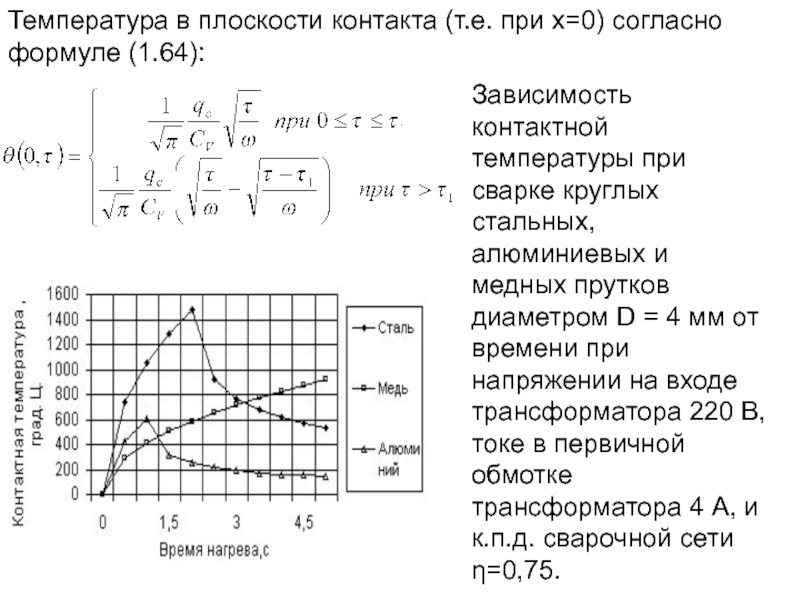
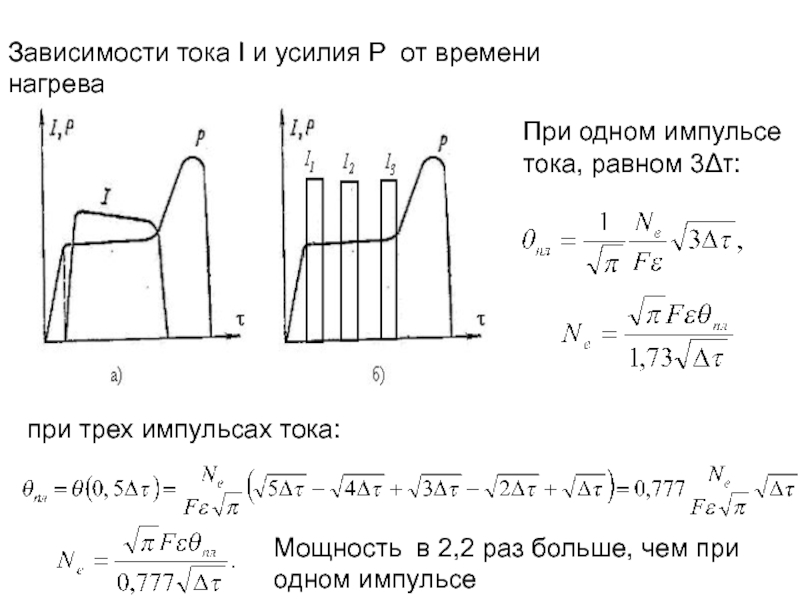
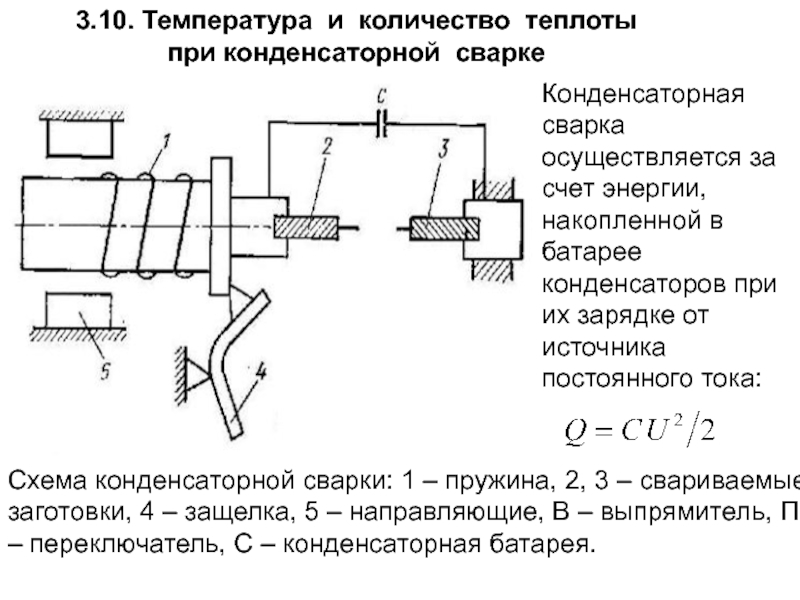
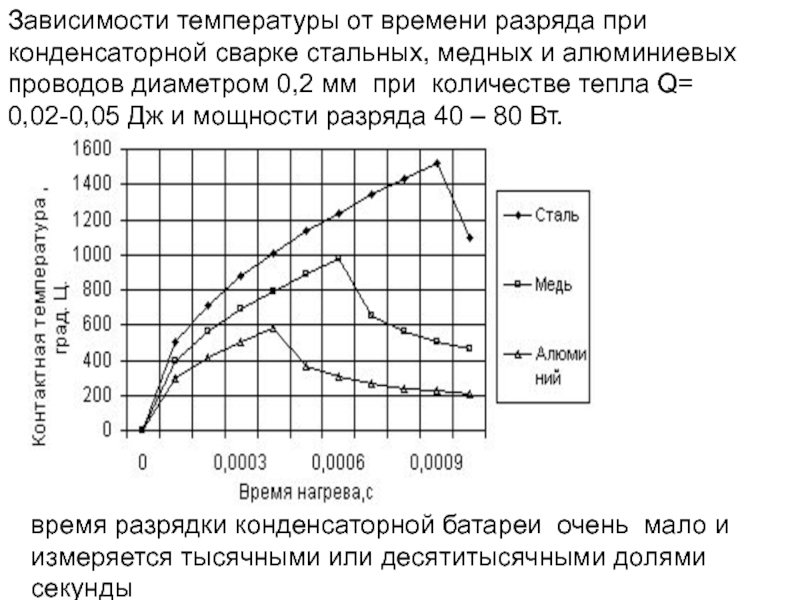

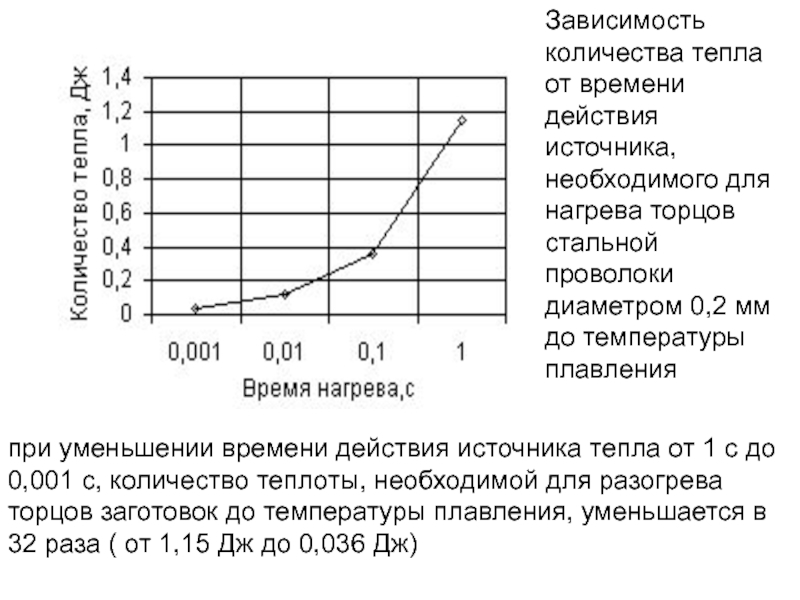
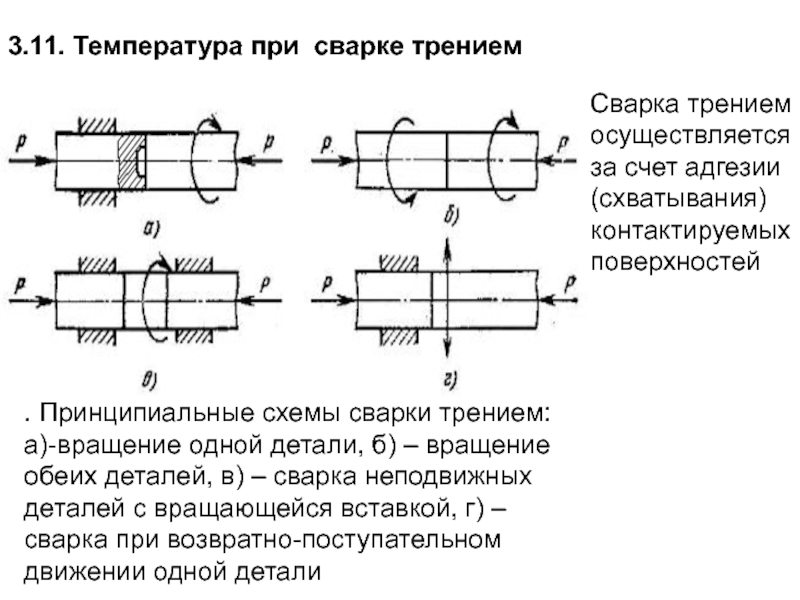

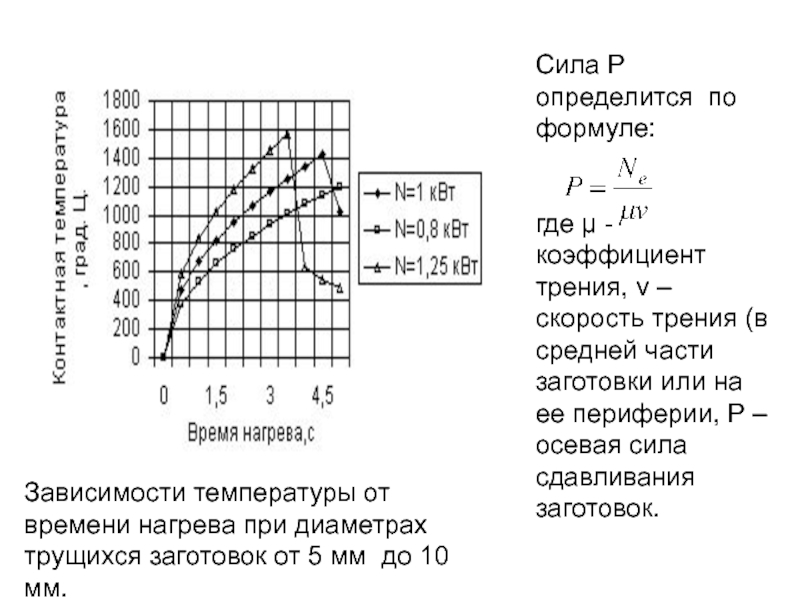
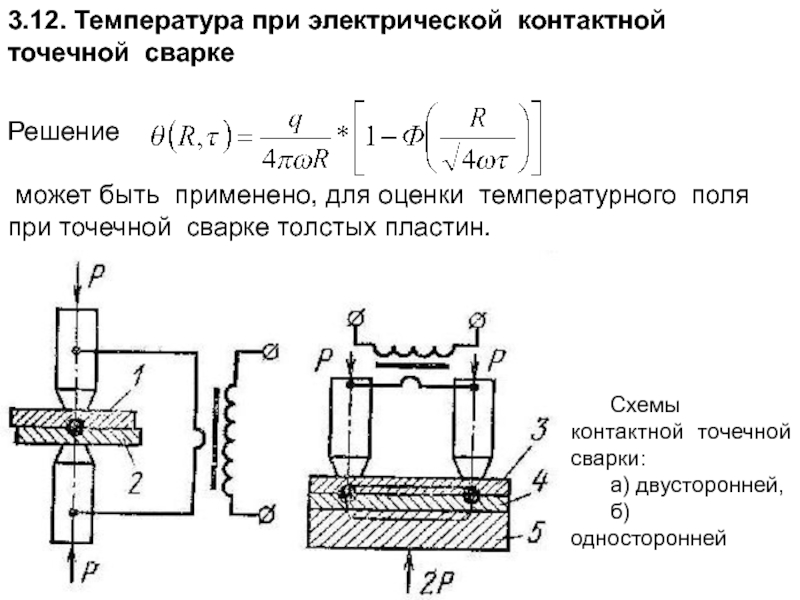
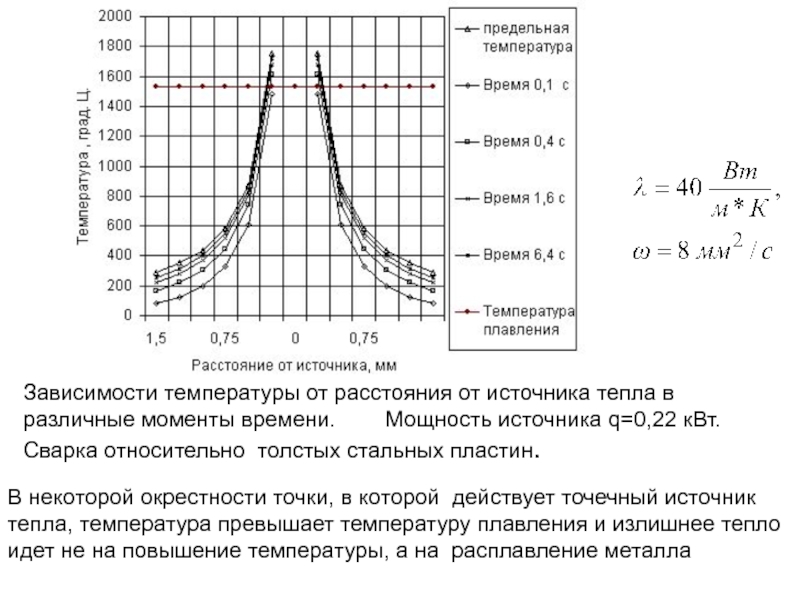
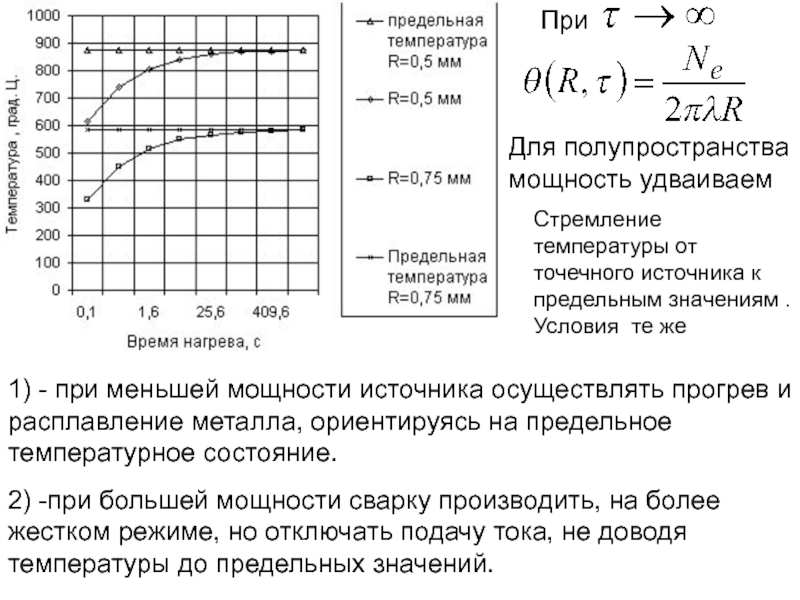
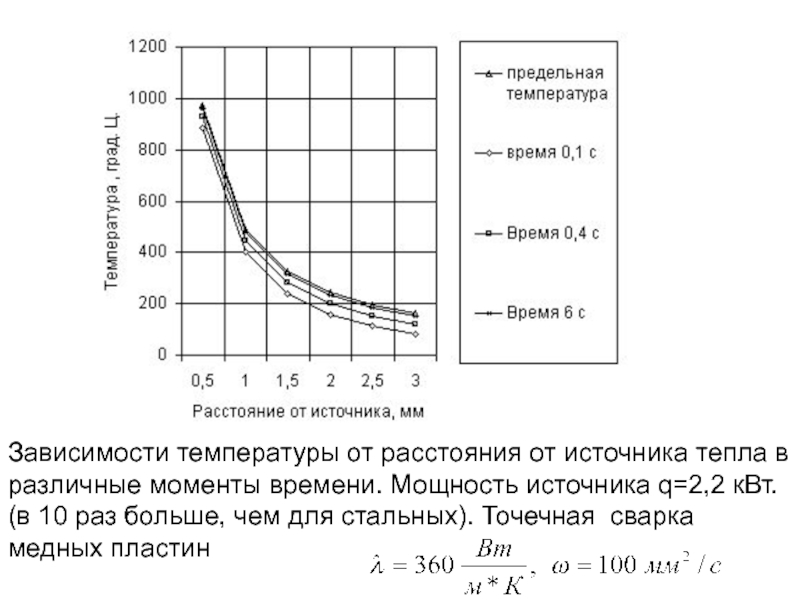
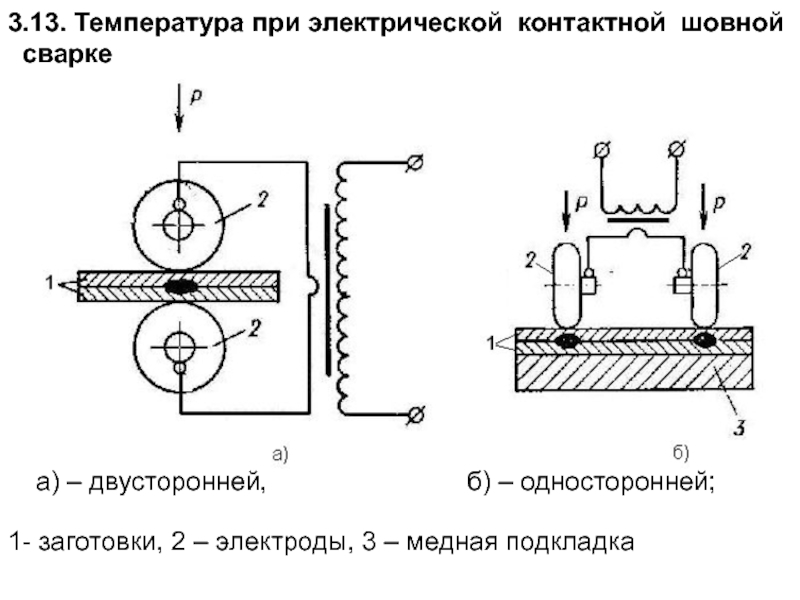

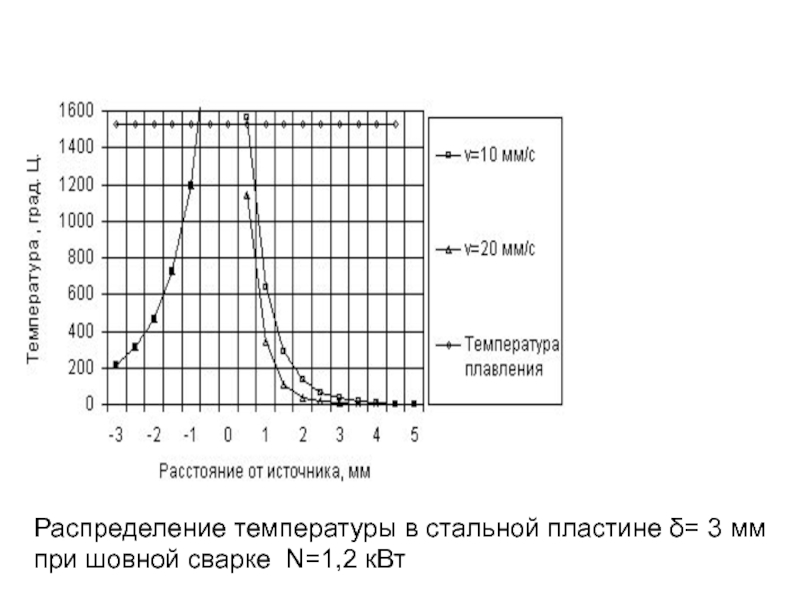
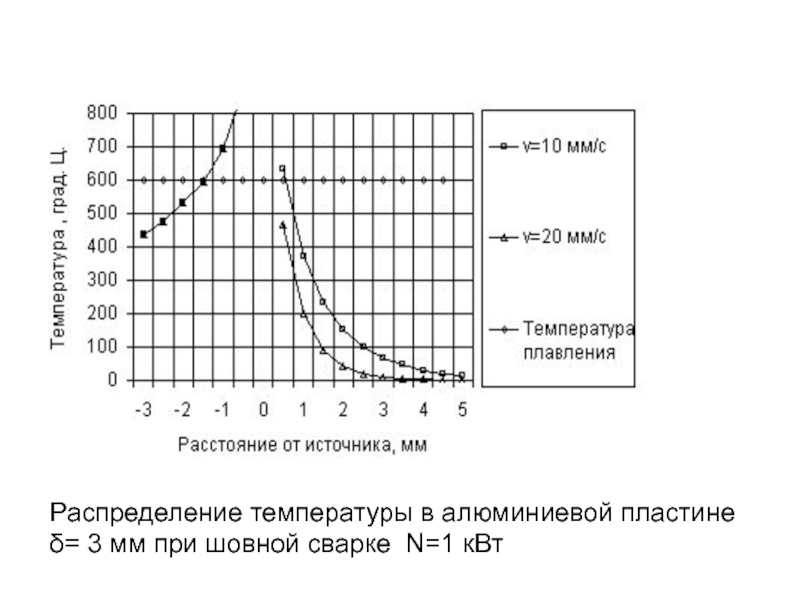
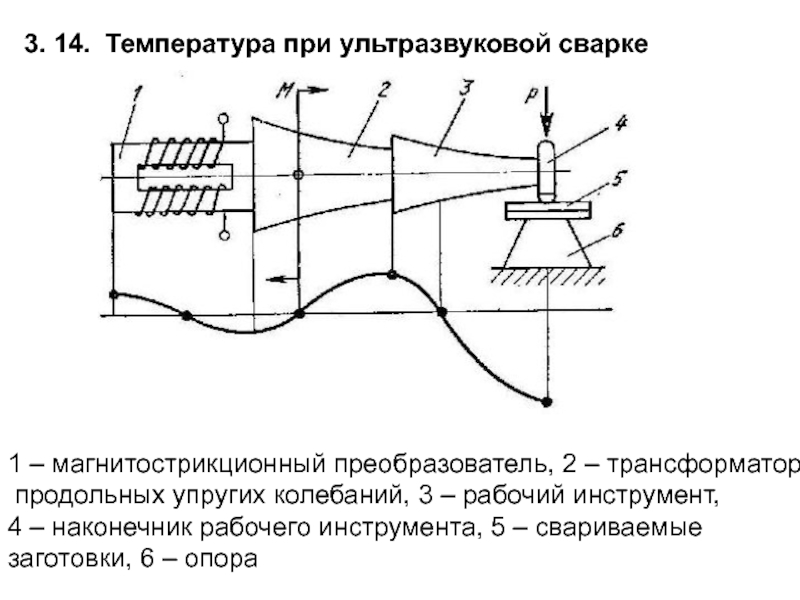
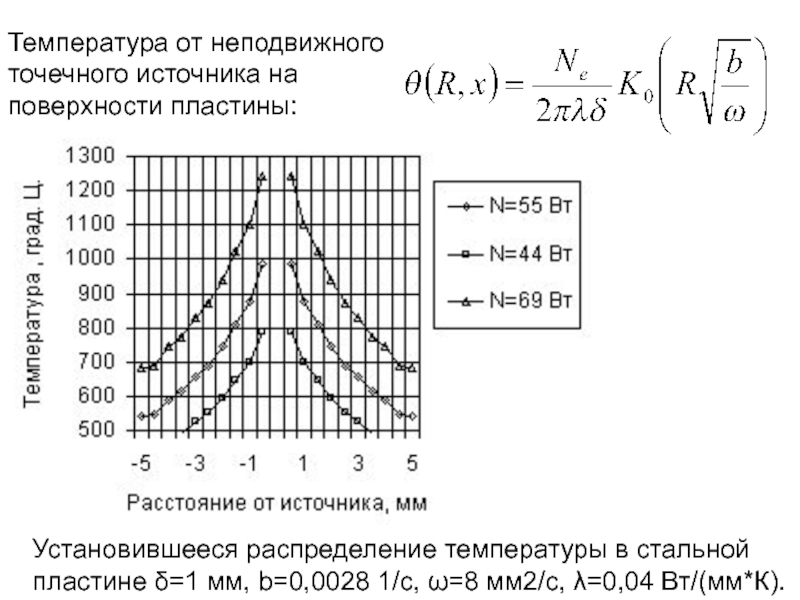

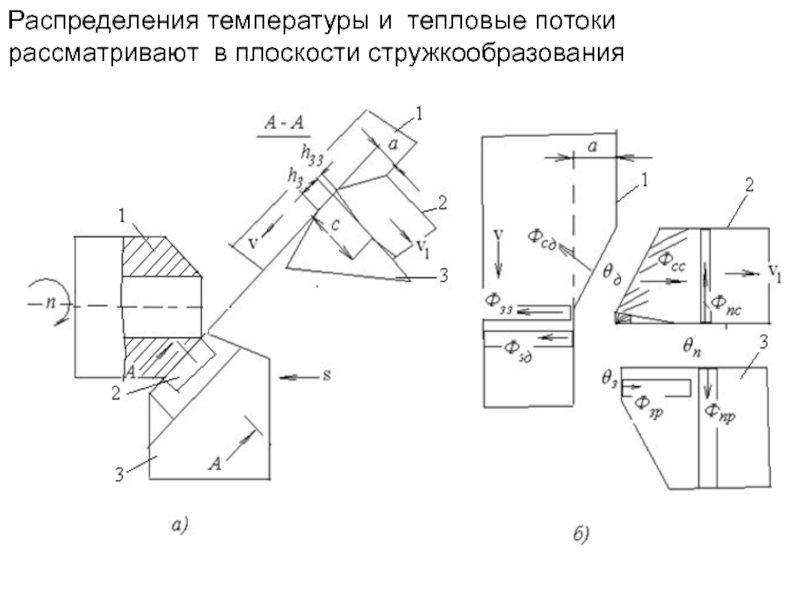

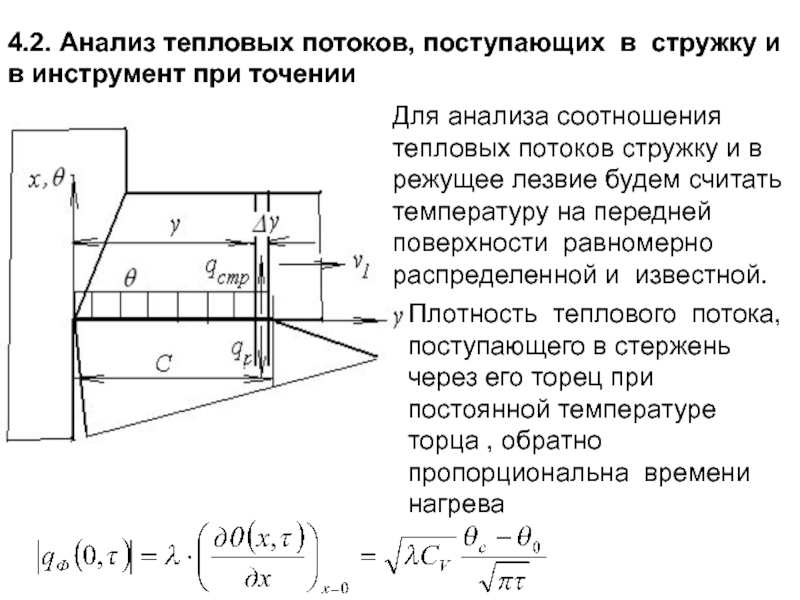

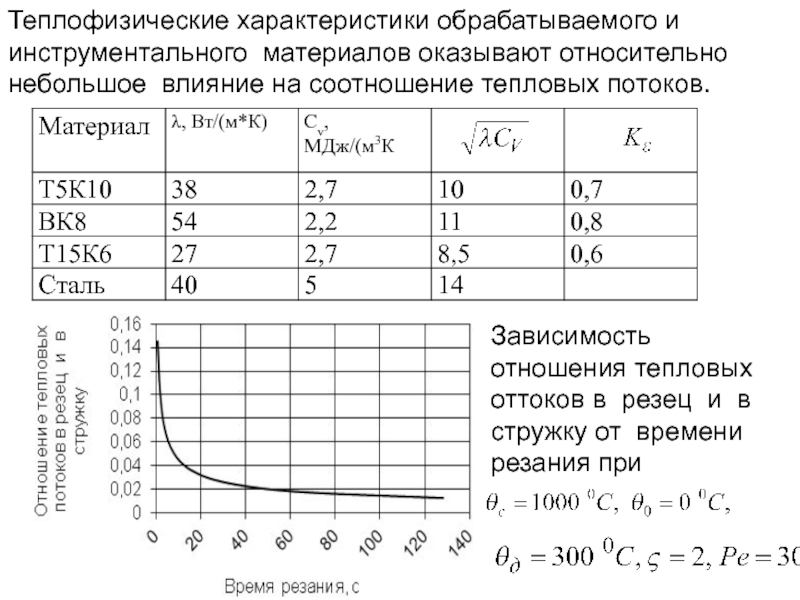
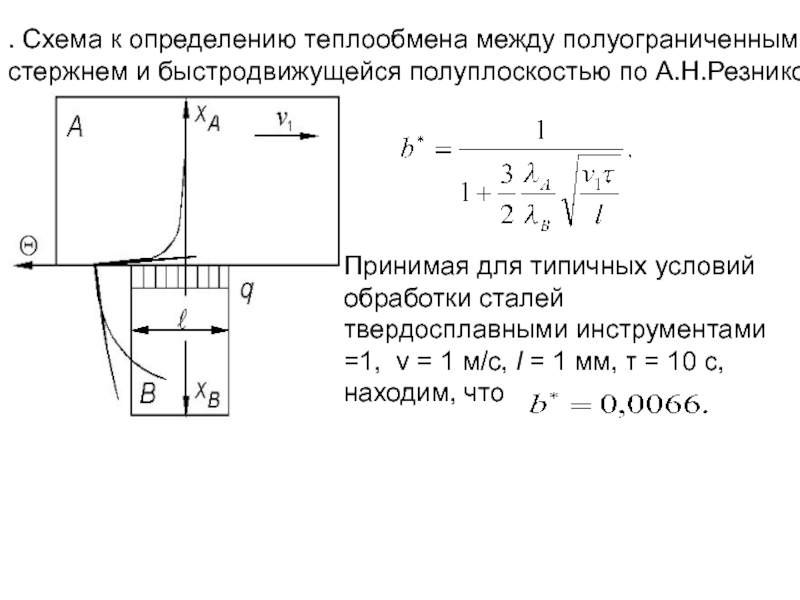
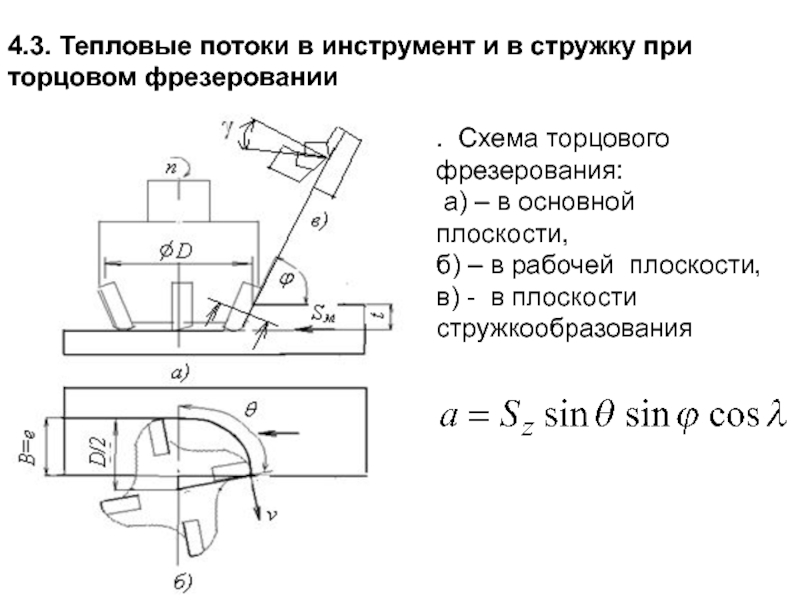

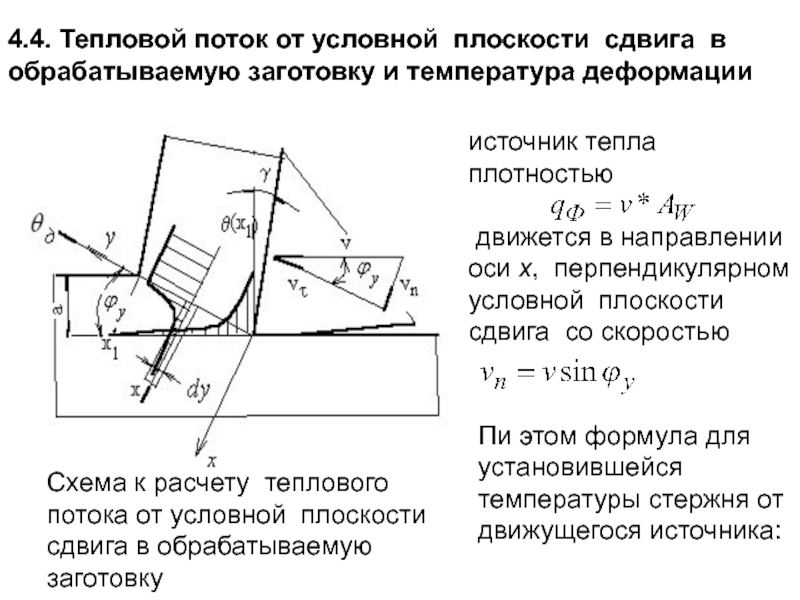
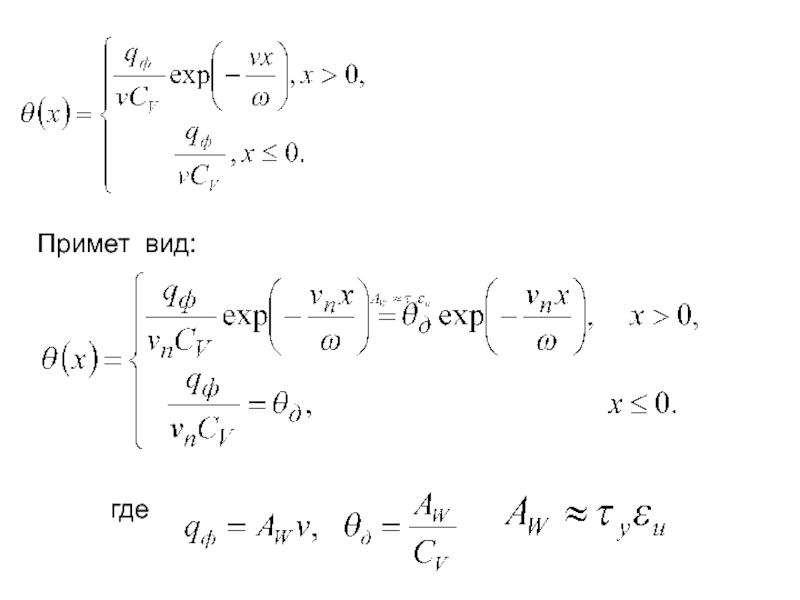

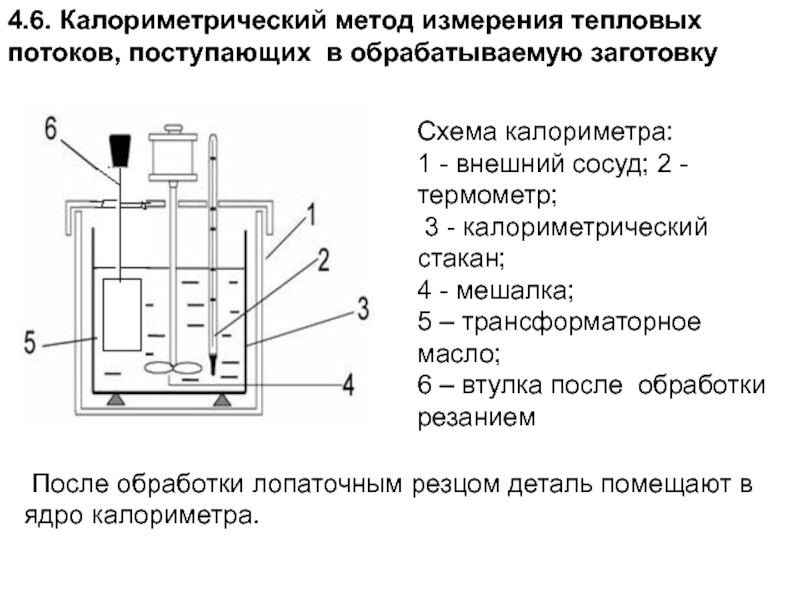
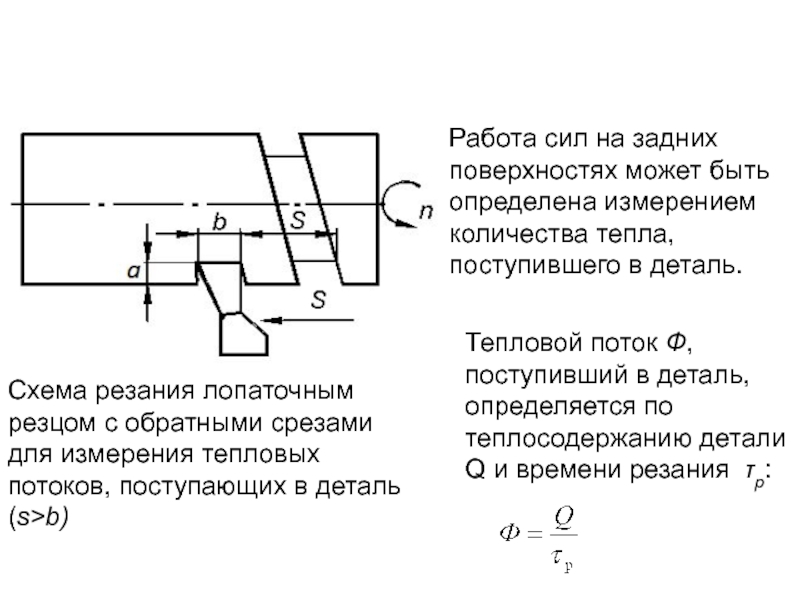
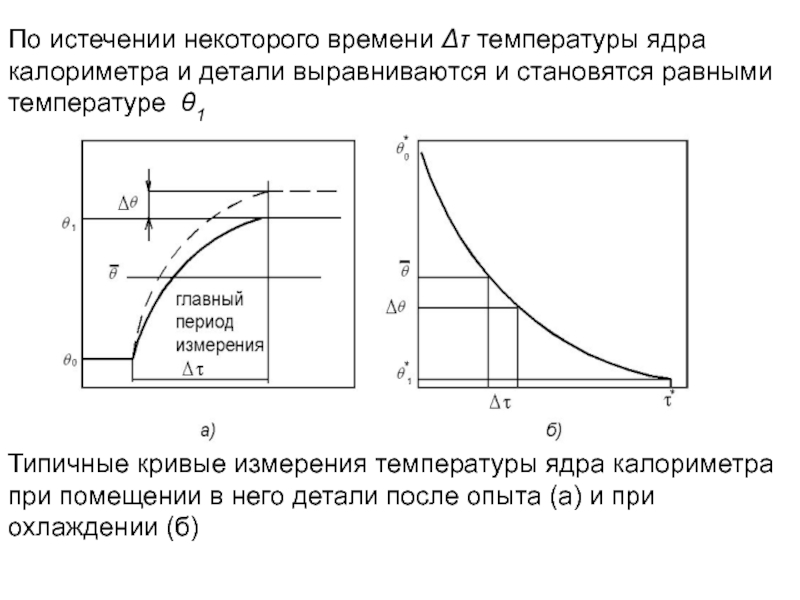



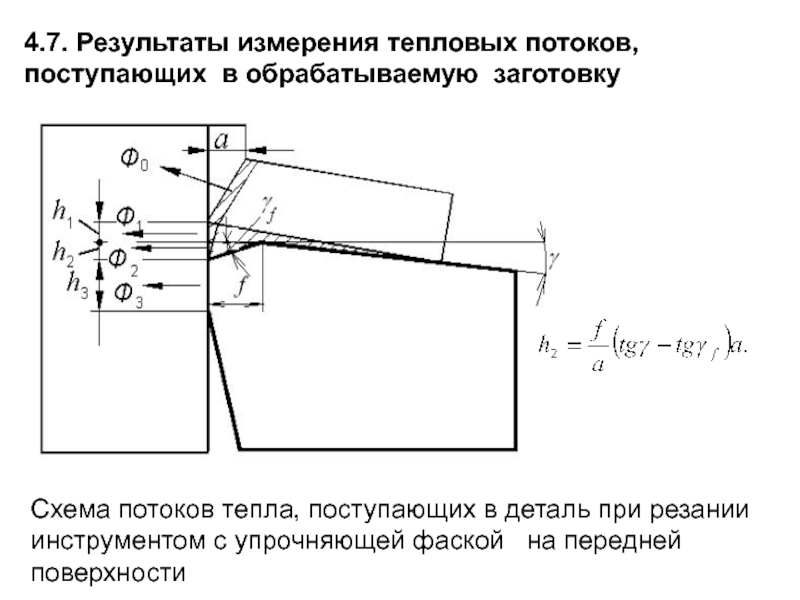
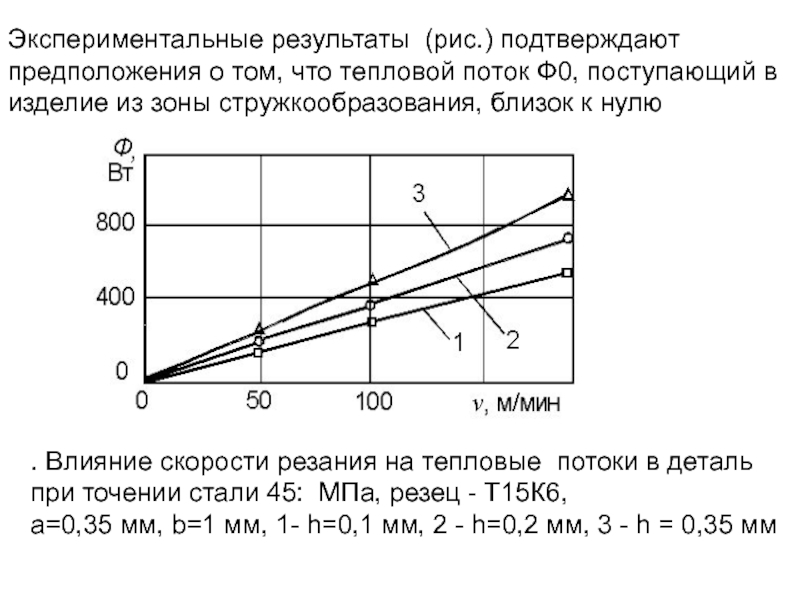
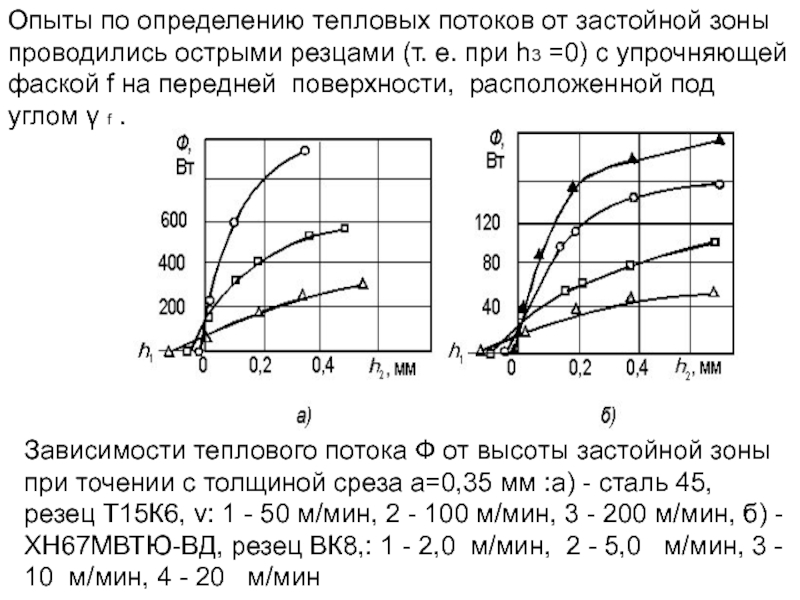
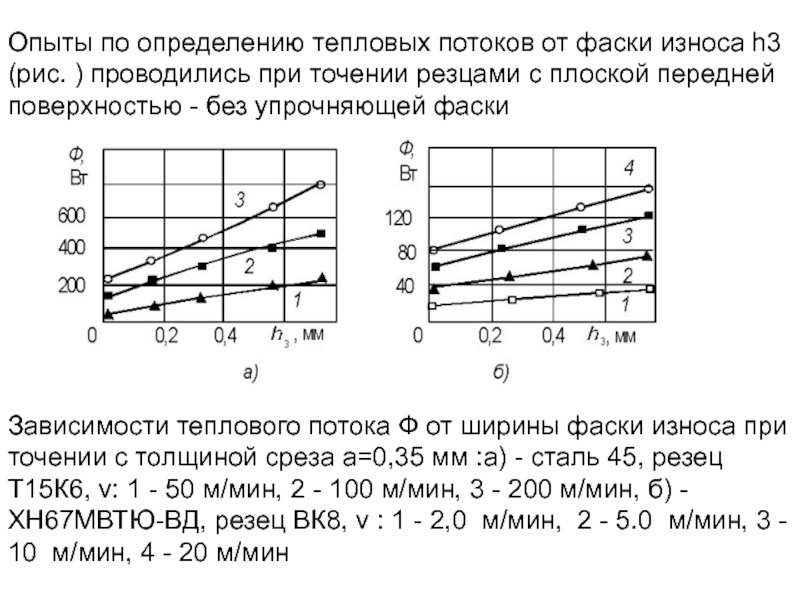
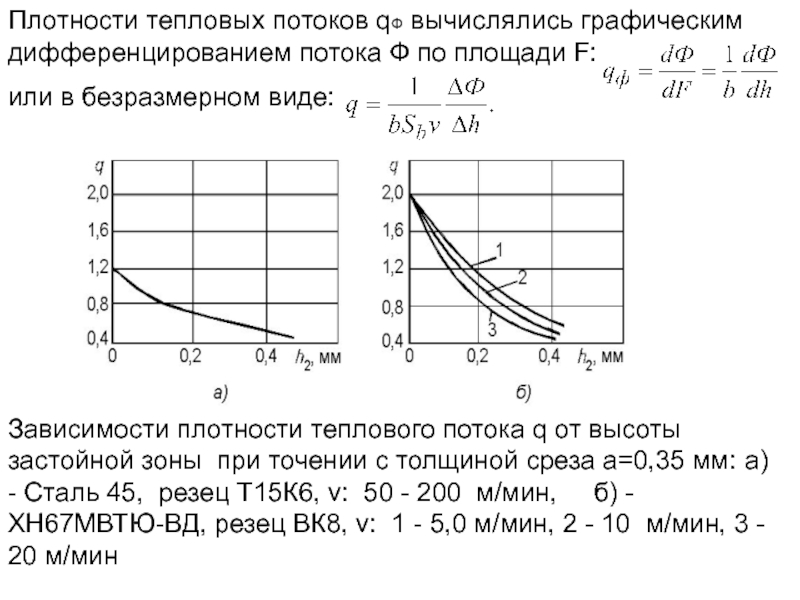

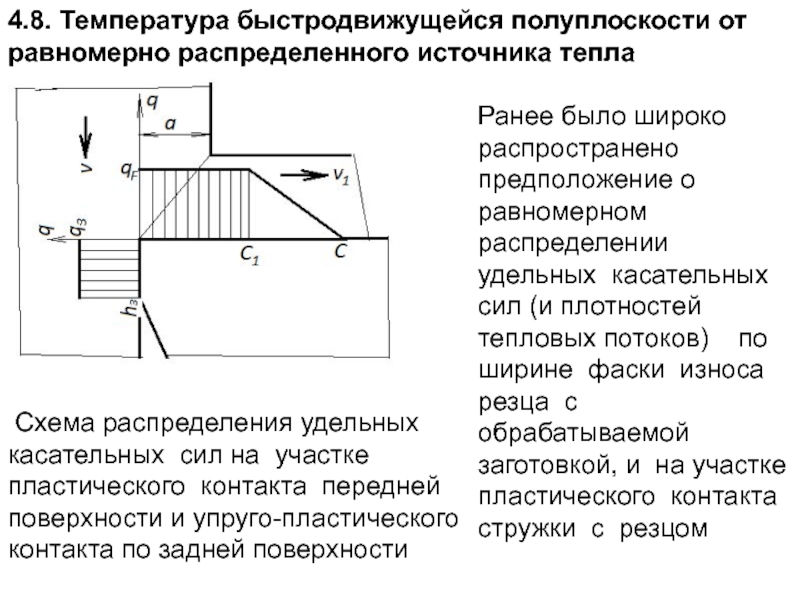
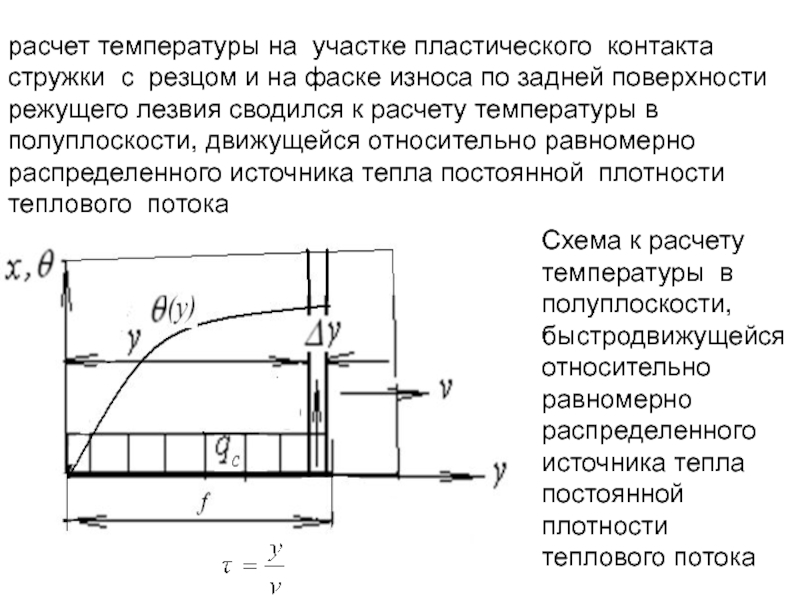

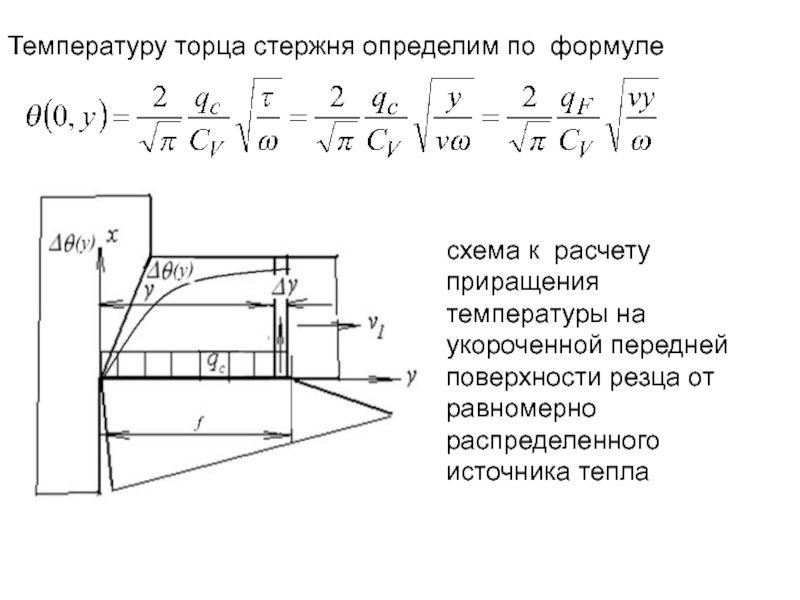

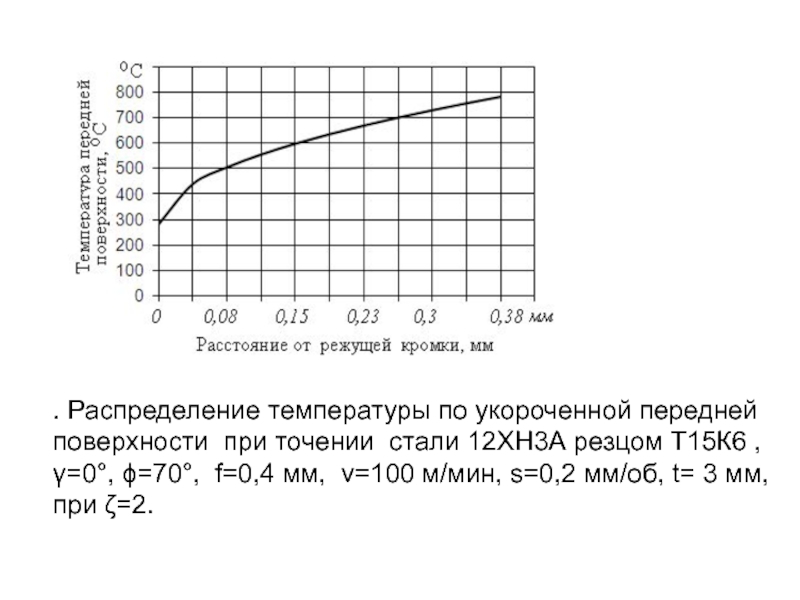
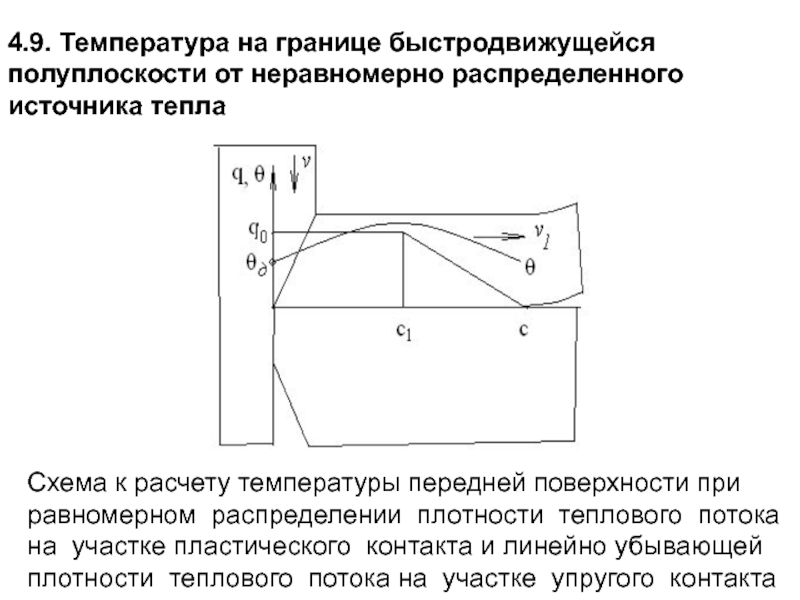

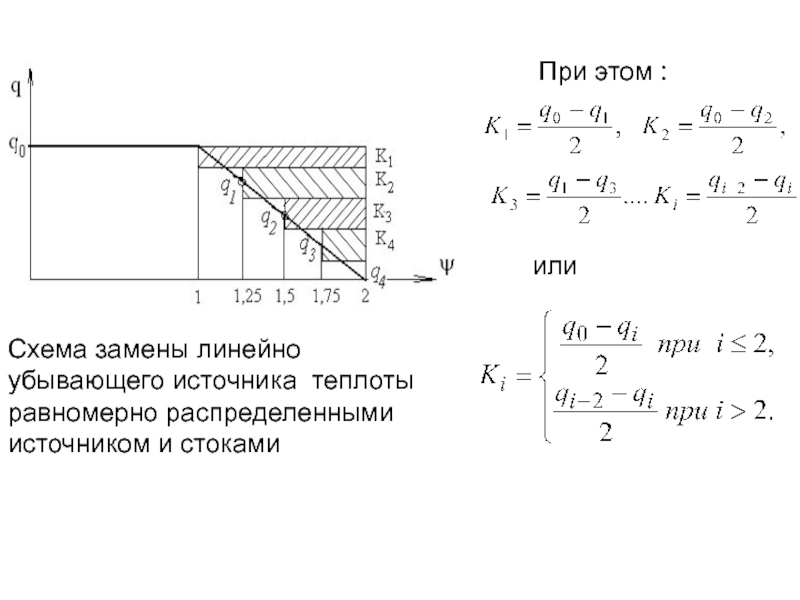

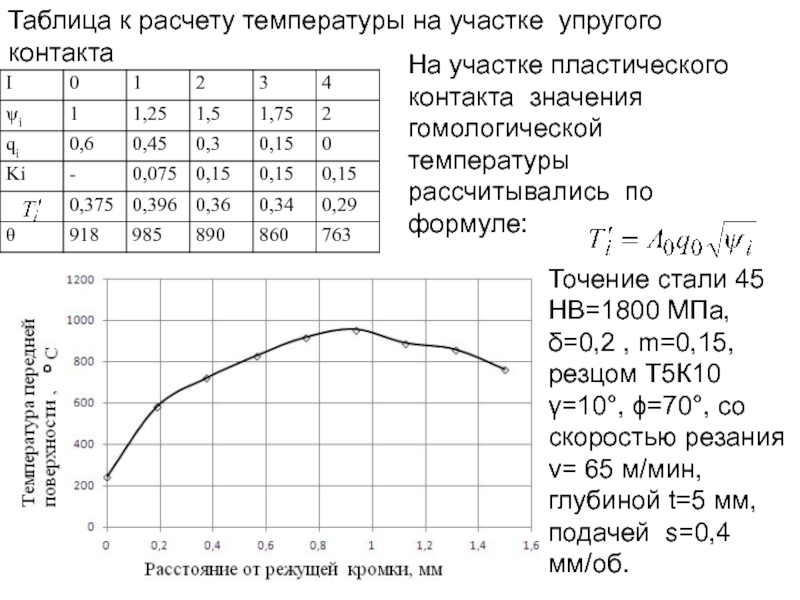
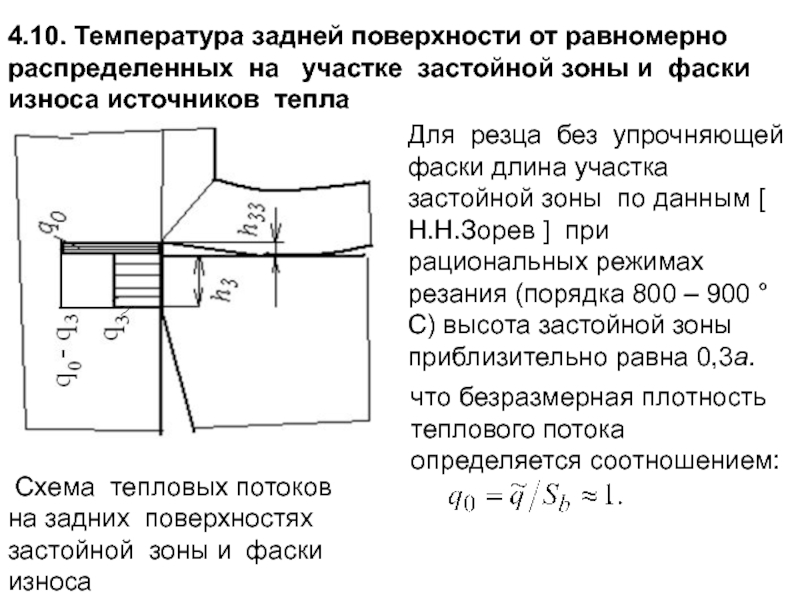
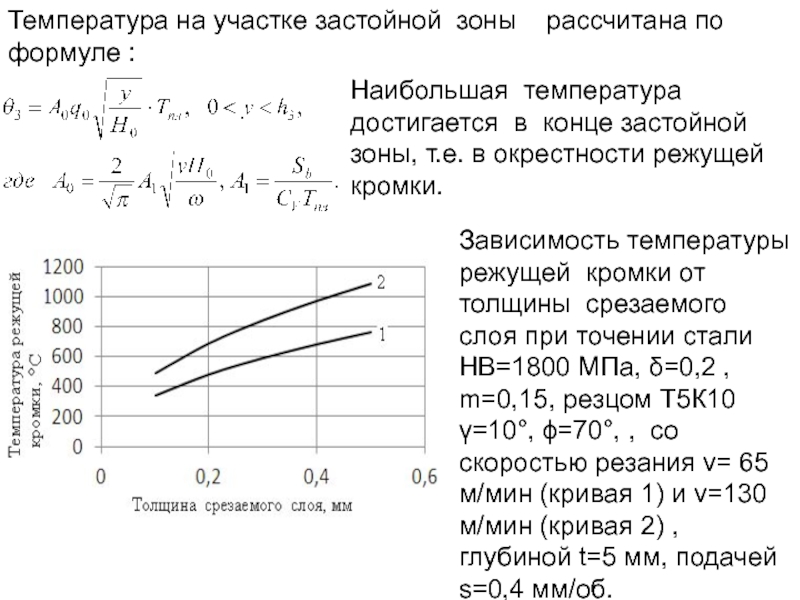
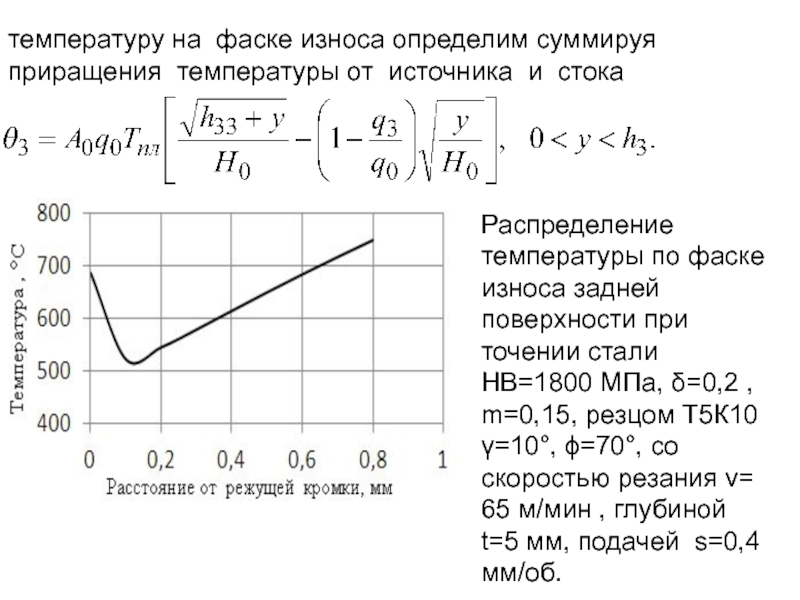
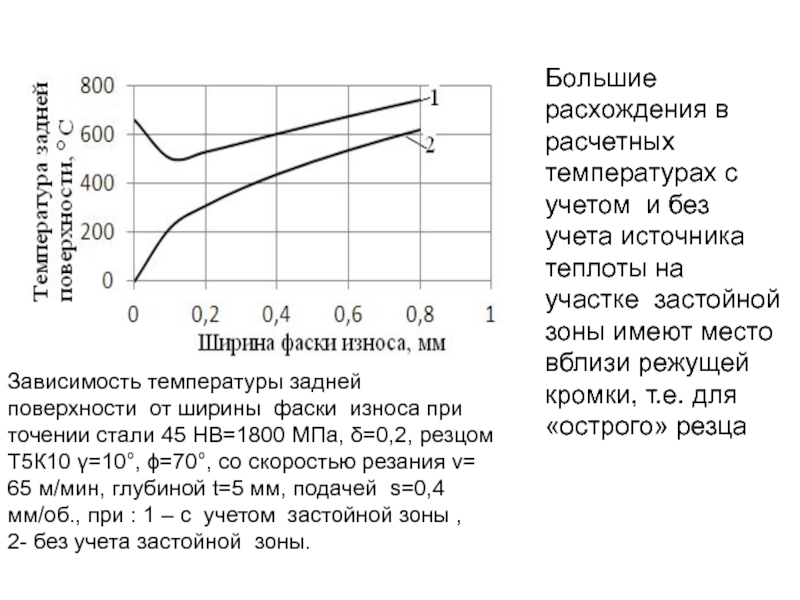
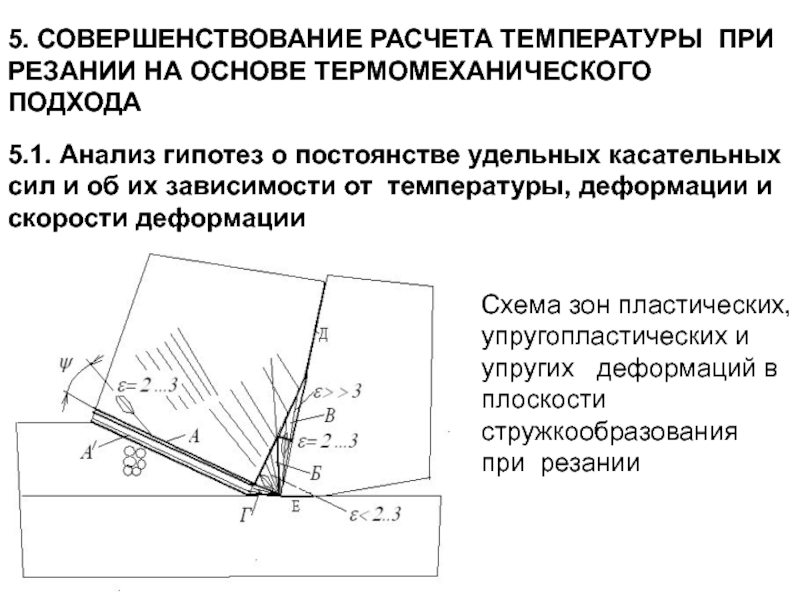
![На основании данных Н.Н.Зорева [ ] о силах резания и усадке стружки](/img/tmb/5/430656/95299178c62930668534df88832c1ec5-800x.jpg)
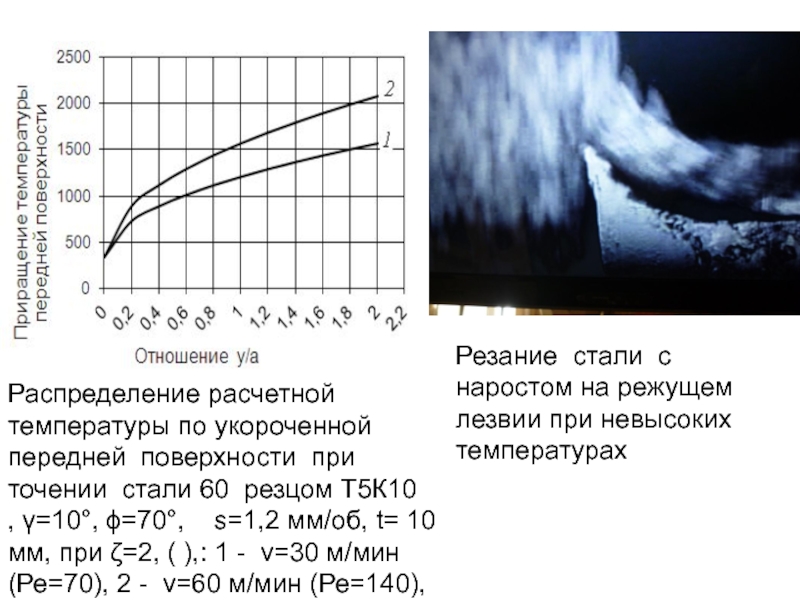
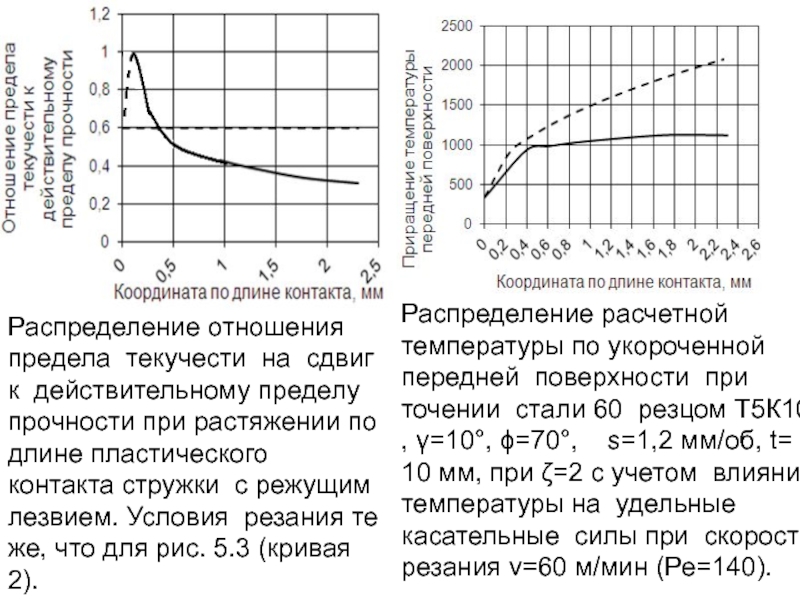
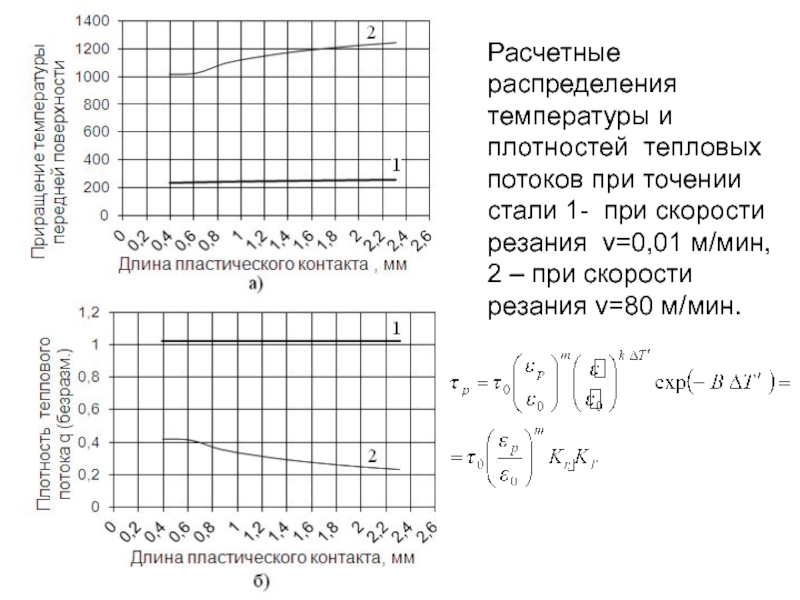

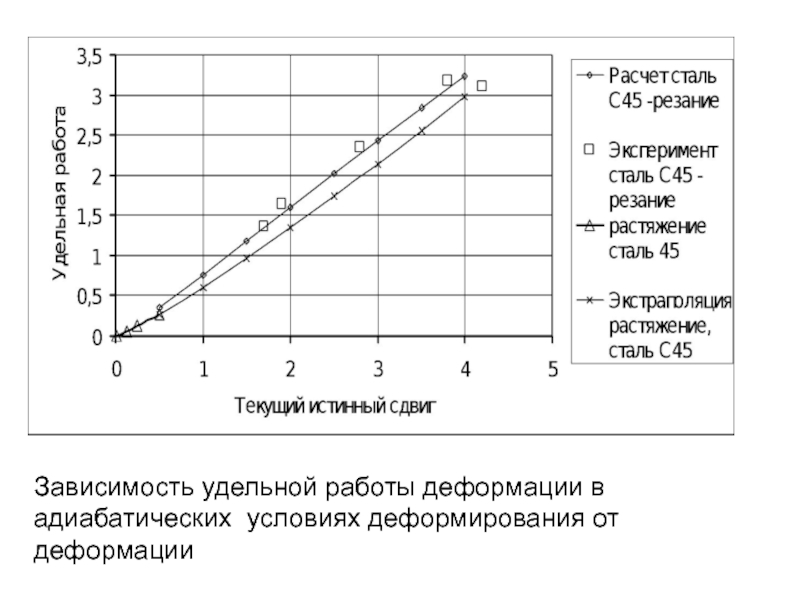
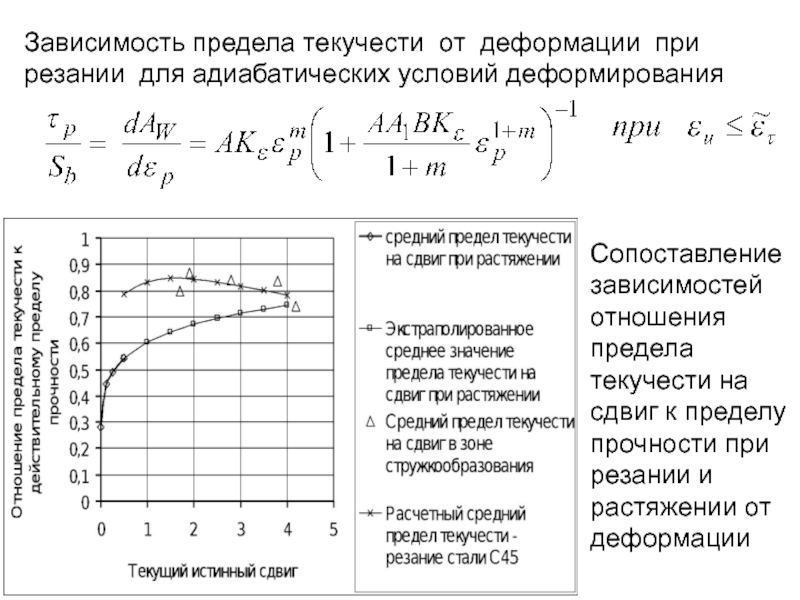

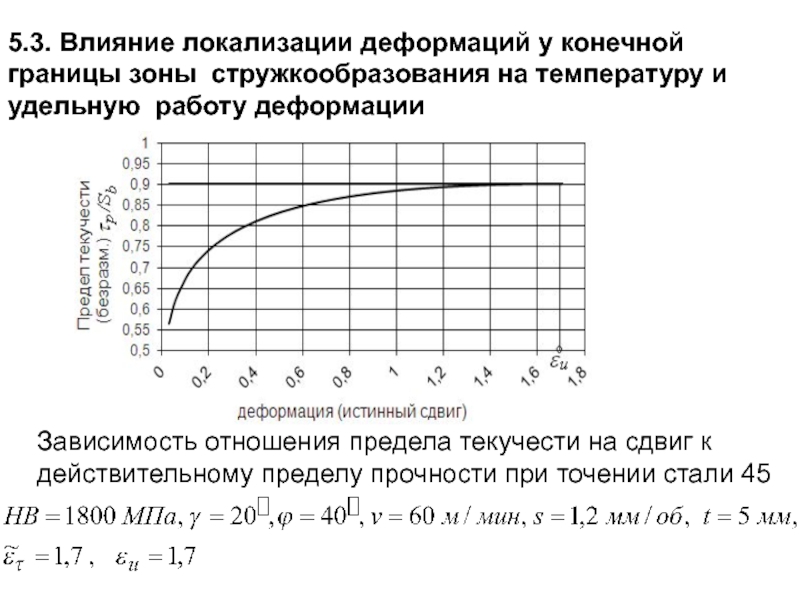


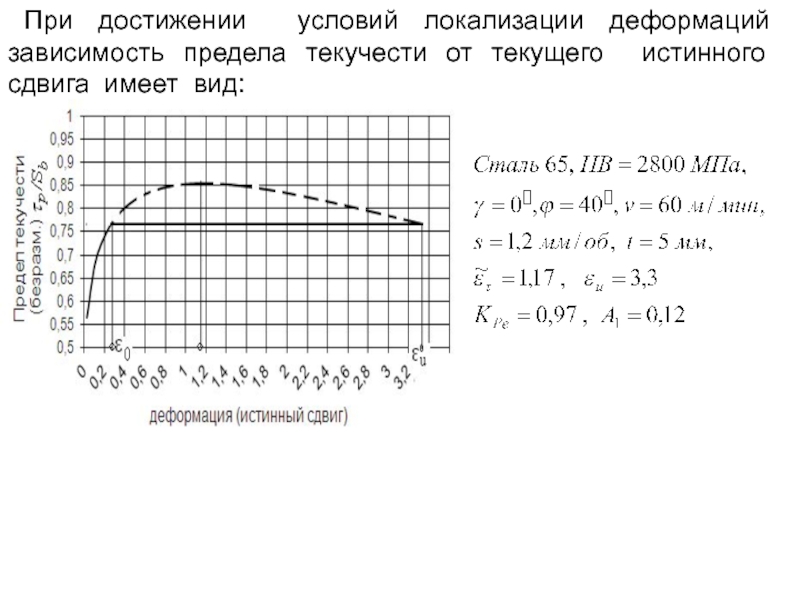
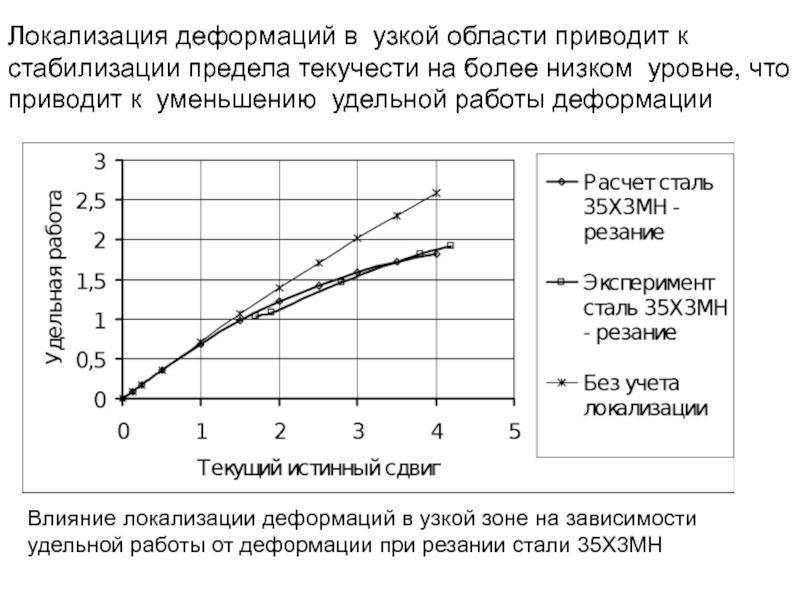

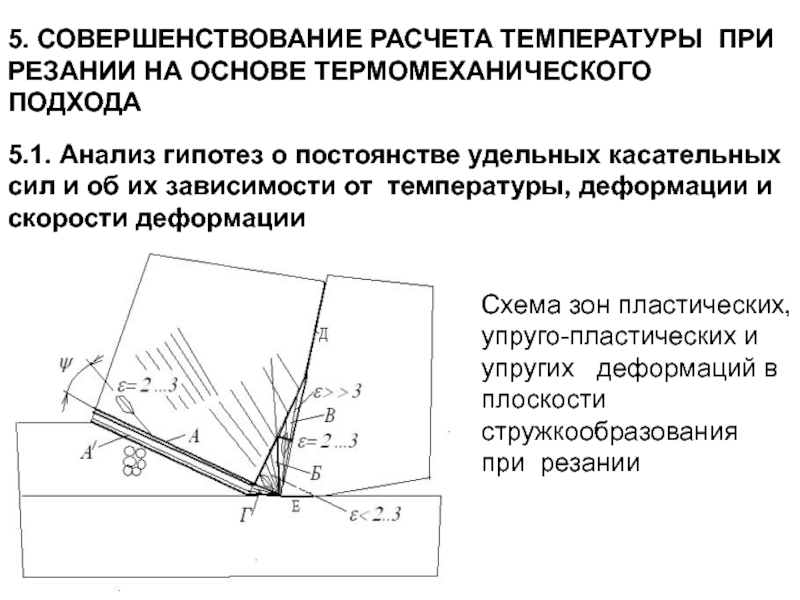
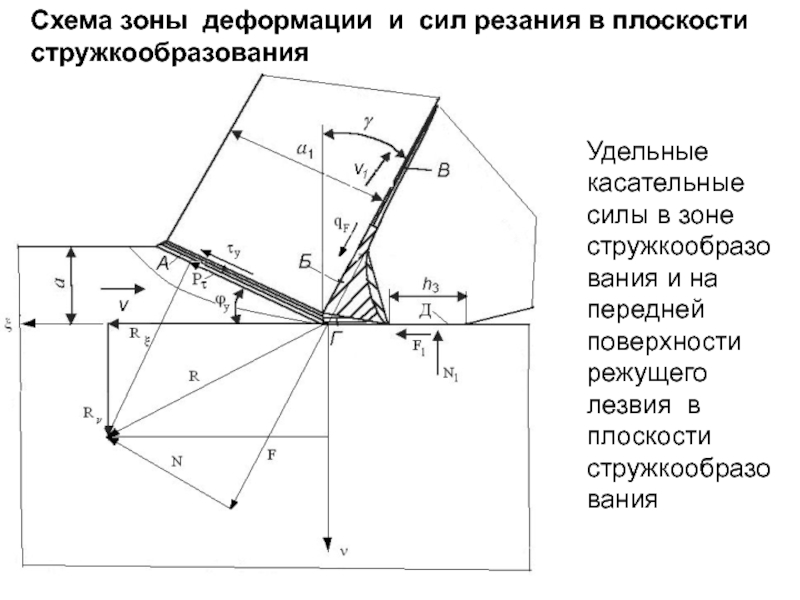
![На основании данных Н.Н.Зорева [ ] о силах резания и усадке стружки](/img/tmb/5/430656/3562c6d4fc21053536f8f86c24b3b9e8-800x.jpg)
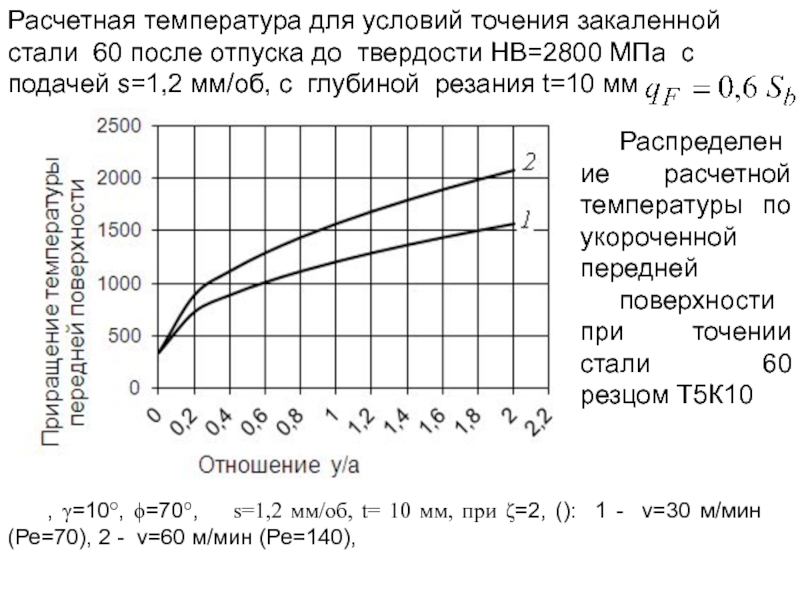
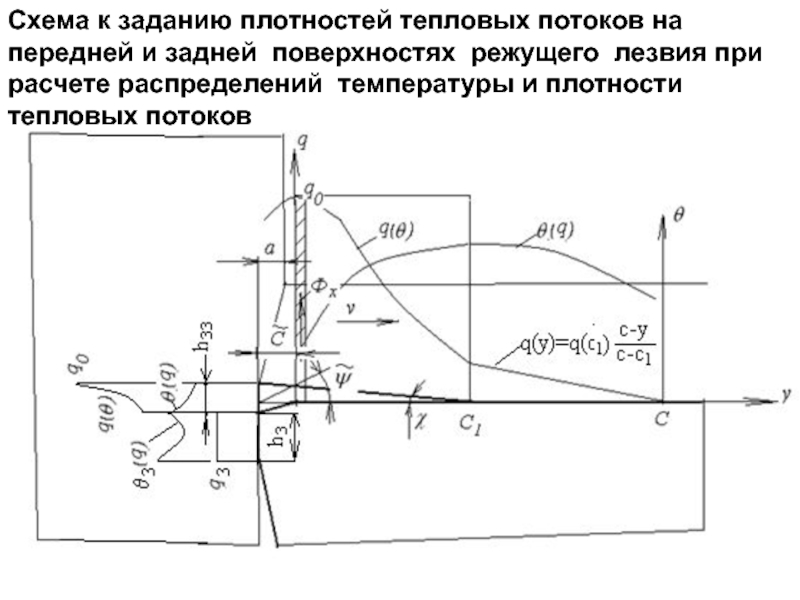
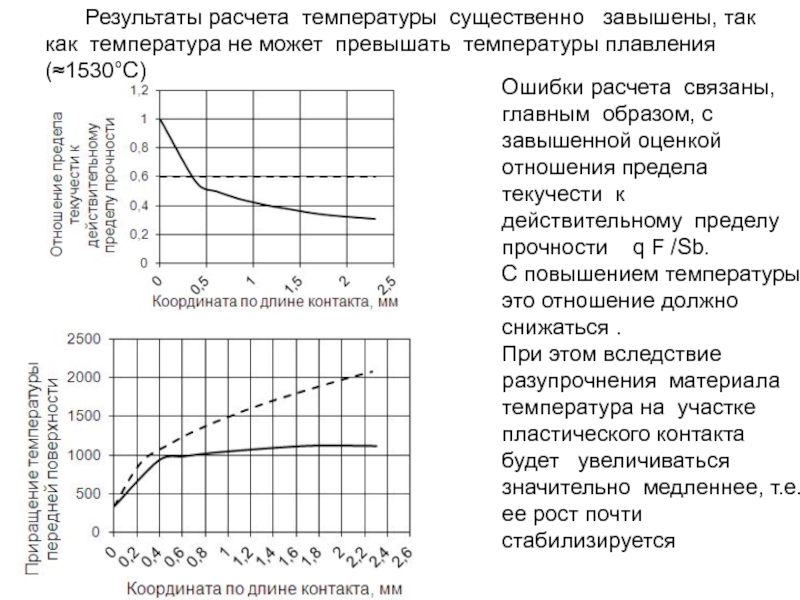
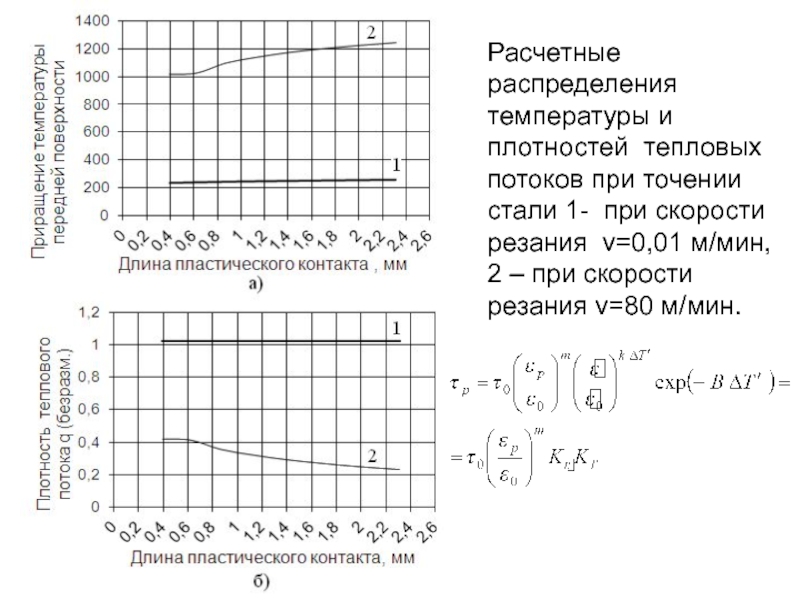
![. Резание стали с наростом на режущем лезвии при невысоких температурах [ ]](/img/tmb/5/430656/eb6bdc9b992843ab406d086180671507-800x.jpg)