- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Федина Галина Ивановнаучитель математики и физики, заместитель директора по учебно-воспитательной работе презентация
Содержание
- 1. Федина Галина Ивановнаучитель математики и физики, заместитель директора по учебно-воспитательной работе
- 2. Теорема Пифагора Учитель математики МОУ СОШ №29«Гармония»
- 3. ТЕОРЕМА
- 4. Задача На охоте с двух отвесных скал
- 5. Вопросы: 1) скалы? 2) расстояние между ними?
- 6. Анализ задачи позволяет заключить, что на
- 7. Если бы зависимость между катетами и гипотенузой
- 8. ВОЗНИКАЕТ ПРОБЛЕМА: Существует ли зависимость между гипотенузой
- 9. Задание Построить прямоугольные треугольники с катетами 3
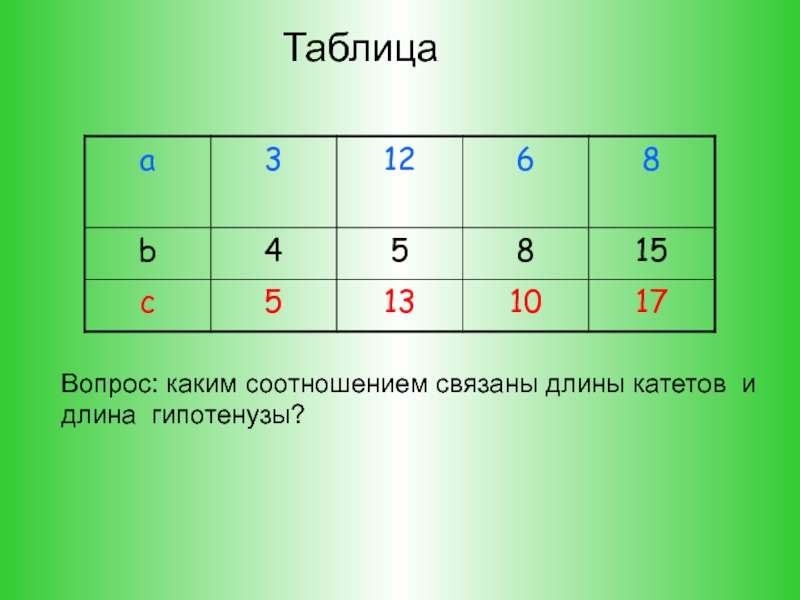
- 10. Таблица Вопрос: каким соотношением связаны длины катетов и длина гипотенузы?
- 11. Прямоугольный треугольник со сторонами 3,
- 12. Если дан нам треугольник,
- 13. Одно из доказательств теоремы ПИФАГОРА
- 14. Доказательство индийского математика Басхары изображено на рисунке.
- 15. Пребудет вечной истина, как скоро Ее познает
- 16. Поэтому всегда с тех самых
- 17. Пример практического применения теоремы ПИФАГОРА В зданиях
- 18. В романской архитектуре часто встречается мотив, представленный
- 19. История ТЕОРЕМЫ Исторический обзор начнем с древнего
- 20. Кантор (крупнейший немецкий историк математики)
- 21. Несколько больше известно о теореме Пифагора у
- 22. Геометрия у индусов, как и у египтян
- 23. БИОГРАФИЯ ПИФАГОРА Великий ученый Пифагор родился около
- 24. Страсть к музыке и поэзии великого Гомера
- 25. В 548 г. до н.э. Пифагор прибыл
- 26. Поэтому, научившись всему, что дали ему жрецы,
- 27. А на Самосе в то время царствовал
- 28. Но в 530 г. до н.э. Кир
- 29. В Кротоне Пифагор учредил нечто вроде религиозно-этического
- 30. …Прошло 20 лет. Слава о братстве разнеслась
- 31. На Венере жители красивые Отвели землянина на
- 32. Исторические
- 33. Задача индийского математика XII века Бхаскары
- 34. Задача из китайской "Математики в девяти
- 35. Задача из учебника "Арифметика" Леонтия Магницкого
- 36. ПИФАГОРОВА ГОЛОВОЛОМКА Из семи частей квадрата
Слайд 1Федина Галина Ивановна
учитель математики и физики, заместитель директора по учебно-воспитательной работе
Слайд 2Теорема Пифагора
Учитель математики МОУ СОШ №29«Гармония» Федина Г.И.
Ученица 8Б класса МОУ
СОШ № 29«Гармония»
Даниелова Э.
Даниелова Э.
Слайд 3
ТЕОРЕМА
ПИФАГОРА
Суть истины вся в
том, что нам она – навечно,
Когда хоть раз в прозрении её увидим свет,
И теорема Пифагора через столько лет
Для нас. Как для него, бесспорна, безупречна …
(Отрывок из стихотворения А. Шамиссо)
Слайд 4Задача
На охоте с двух отвесных скал два охотника заметили козла и
одновременно в него выстрелили, причём стрелы достигли цели одновременно. Охотники одновременно начали спуск к добыче с одинаковой скоростью. Кто быстрее из охотников доберется до козла?
Слайд 5Вопросы:
1) скалы?
2) расстояние между ними?
3) путь каждой стрелы?
4) путь каждого охотника?
5)
что означает факт, что стрелы достигли цели одновременно?
Слайд 6Анализ задачи позволяет заключить,
что на данном этапе задачу решить
нельзя,
так как невозможно сравнить равенство отрезков ДС и СЕ, которые являются гипотенузами прямоугольных треугольников.
Слайд 7Если бы зависимость между катетами и гипотенузой в прямоугольном треугольнике была
известной, то можно было бы в каждом треугольнике выразить гипотенузу через катеты и сравнить полученные выражения.
Слайд 8ВОЗНИКАЕТ ПРОБЛЕМА:
Существует ли зависимость между гипотенузой и катетами в прямоугольном треугольнике,
и, если она существует, то как она формулируется?
Слайд 9Задание
Построить прямоугольные треугольники с катетами 3 и 4, 12 и 5,
6 и 8, 8 и 15 и измерить гипотенузу. Результаты занести в таблицу.
Слайд 11 Прямоугольный треугольник со сторонами 3, 4 и 5 ед.
Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен ещё древним египтянам. Они использовали этот треугольник в "правиле верёвки" для построения прямых углов при закладке зданий, храмов, алтарей…
Замечание:
Слайд 12
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим-
И таким простым путём
К результату мы придём.
(И. Дырченко)
Катеты в квадрат возводим,
Сумму степеней находим-
И таким простым путём
К результату мы придём.
(И. Дырченко)
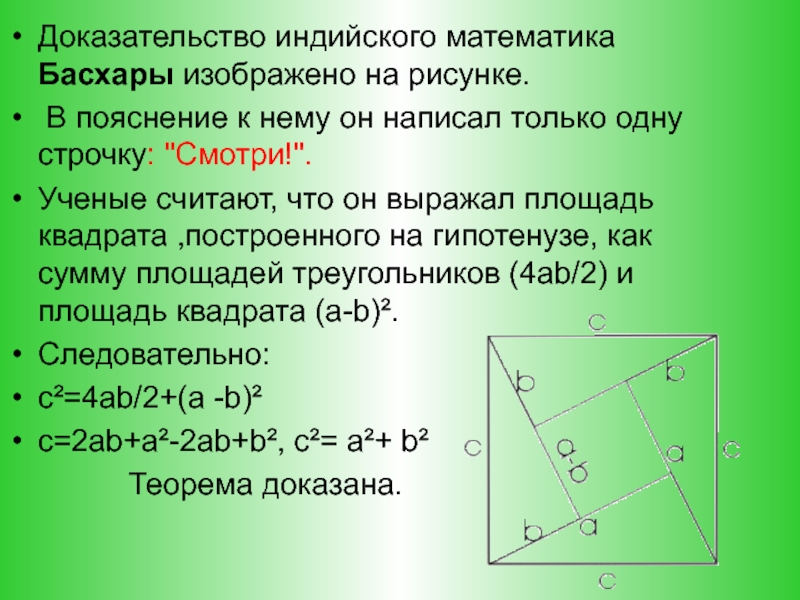
Слайд 14Доказательство индийского математика Басхары изображено на рисунке.
В пояснение к нему
он написал только одну строчку: "Смотри!".
Ученые считают, что он выражал площадь квадрата ,построенного на гипотенузе, как сумму площадей треугольников (4ab/2) и площадь квадрата (a-b)².
Следовательно:
c²=4ab/2+(a -b)²
c=2ab+a²-2ab+b², c²= a²+ b²
Теорема доказана.
Ученые считают, что он выражал площадь квадрата ,построенного на гипотенузе, как сумму площадей треугольников (4ab/2) и площадь квадрата (a-b)².
Следовательно:
c²=4ab/2+(a -b)²
c=2ab+a²-2ab+b², c²= a²+ b²
Теорема доказана.
Слайд 15 Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема
Пифагора
Верна, как и в его далекий век. Обильно было жертвопринашенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков.
Верна, как и в его далекий век. Обильно было жертвопринашенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков.
Слайд 16 Поэтому всегда с тех самых пор,
Чуть истина
рождается на свет,
Быки ревут, ее почуя ,вслед.
Они не в силах свету помешать , А могут лишь закрыв глаза дрожать От страха, что вселил в них Пифагор.
Быки ревут, ее почуя ,вслед.
Они не в силах свету помешать , А могут лишь закрыв глаза дрожать От страха, что вселил в них Пифагор.
Слайд 17Пример практического применения теоремы ПИФАГОРА
В зданиях готического и ромaнского стиля верхние
части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле.
Способ построения его очень прост.
Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг половине ширины, (b/2) для внутренних дуг .Остается еще полная окружность, касающаяся четырех дуг.
Способ построения его очень прост.
Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг половине ширины, (b/2) для внутренних дуг .Остается еще полная окружность, касающаяся четырех дуг.
Слайд 18В романской архитектуре часто встречается мотив, представленный на рисунке.
Если b по-прежнему
обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4.
Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p.
Выполнив вычисления , получим : p=
Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p.
Выполнив вычисления , получим : p=
Слайд 19История ТЕОРЕМЫ
Исторический обзор начнем с древнего Китая.
Здесь особое внимание привлекает
математическая
книга Чу-пей.
"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
Слайд 20 Кантор (крупнейший немецкий историк математики) считает, что равенство
3 ² + 4 ² = 5²
было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
Слайд 21Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте,
относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника.
Слайд 22Геометрия у индусов, как и у египтян и вавилонян, была тесно
связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
Слайд 23БИОГРАФИЯ ПИФАГОРА
Великий ученый Пифагор родился около 570 г. до н.э. на
острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.
Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского.
Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского.
Слайд 24Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю
жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера.
Гермодамант ввел юного Пифагора в круг муз .
Ферекид направил взор Пифагора к природе.
Гермодамант ввел юного Пифагора в круг муз .
Ферекид направил взор Пифагора к природе.
Слайд 25В 548 г. до н.э. Пифагор прибыл в Навкратис - самосскую
колонию, где было у кого найти кров и пищу. Изучив язык и религию египтян, он уезжает в Мемфис.
Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания.
Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания.
Слайд 26Поэтому, научившись всему, что дали ему жрецы, он, убежав от них,
двинулся на родину в Элладу.
Однако, проделав часть пути, его захватил в плен Камбиз, царь Вавилона
В Вавилоне Пифагору было чему поучится
Однако, проделав часть пути, его захватил в плен Камбиз, царь Вавилона
В Вавилоне Пифагору было чему поучится
Древний Вавилон
Слайд 27А на Самосе в то время царствовал тиран Поликрат. Конечно же,
Пифагора не устраивала жизнь придворного полу раба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон
Слайд 28Но в 530 г. до н.э. Кир двинулся в поход против
племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину. А на Самосе в то время царствовал тиран Поликрат. Конечно же, Пифагора не устраивала жизнь придворного полу раба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон.
Древний г. Кротон
Слайд 29В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского
ордена ("пифагорейцы"), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принципов достойны подражания и сейчас.
Слайд 30…Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды
к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.
Слайд 31На Венере жители красивые Отвели землянина на базу, А потом страну свою счастливую
Пифагору с радостью показывали…
Слайд 33Задача индийского математика
XII века Бхаскары
"На берегу реки рос
тополь одинокий.
Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?"
Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?"
Слайд 34Задача из китайской
"Математики в девяти книгах"
"Имеется водоем со
стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.
Спрашивается: какова глубина воды и какова длина камыша?"
Спрашивается: какова глубина воды и какова длина камыша?"
Слайд 35Задача из учебника "Арифметика"
Леонтия Магницкого
"Случися некому человеку к
стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп.
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."
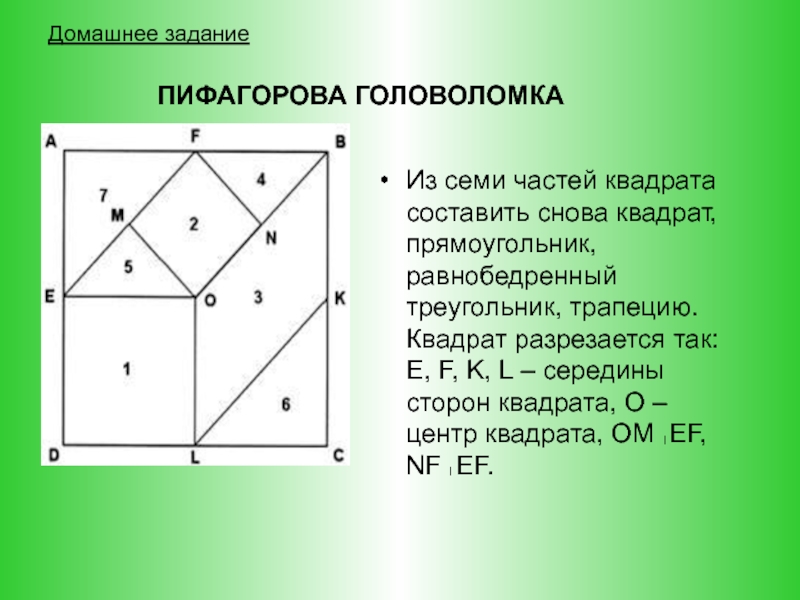
Слайд 36ПИФАГОРОВА ГОЛОВОЛОМКА
Из семи частей квадрата составить снова квадрат, прямоугольник, равнобедренный
треугольник, трапецию. Квадрат разрезается так: E, F, K, L – середины сторон квадрата, О – центр квадрата, ОМ EF, NF EF.
Домашнее задание