(9B)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Fast Frequency and Response Measurements using FFTs презентация
Содержание
- 1. Fast Frequency and Response Measurements using FFTs
- 2. Accurately Detect a Tone What is
- 3. Presentation Overview Why use the frequency domain?
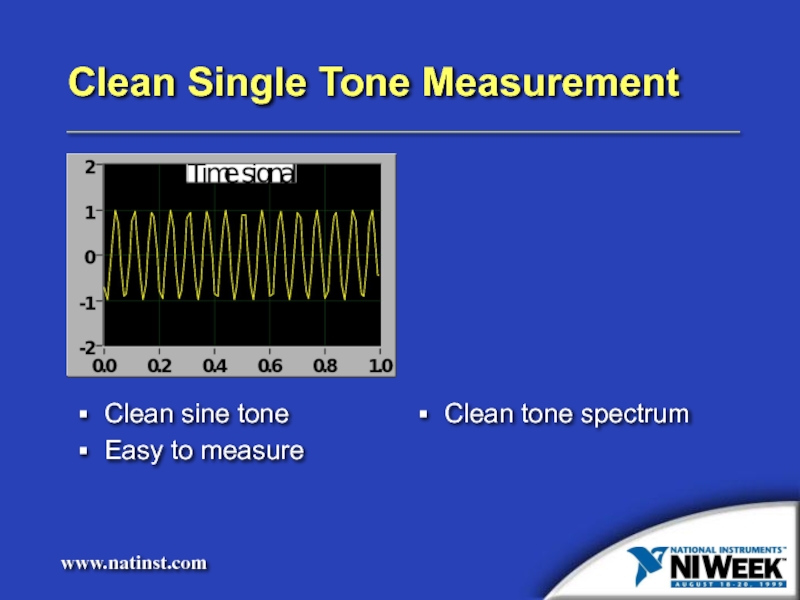
- 4. Clean Single Tone Measurement Clean sine tone Easy to measure Clean tone spectrum
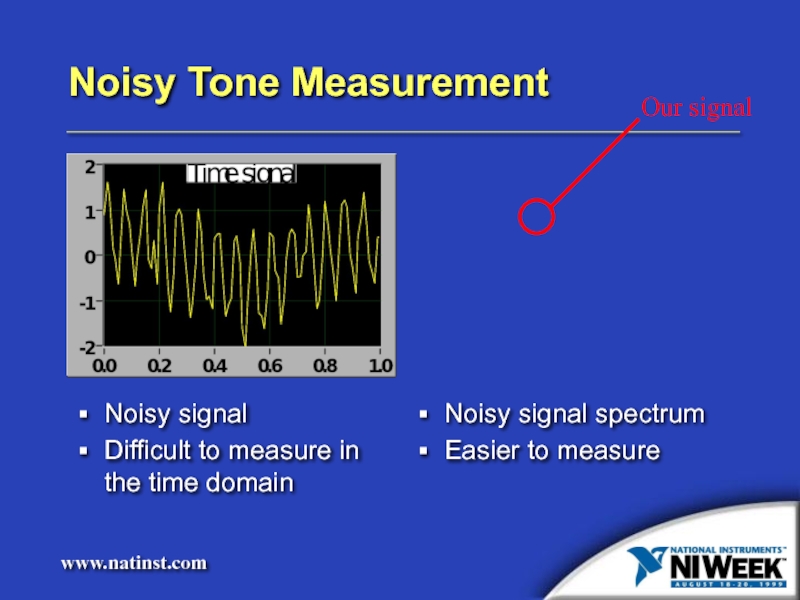
- 5. Noisy Tone Measurement Noisy signal Difficult to
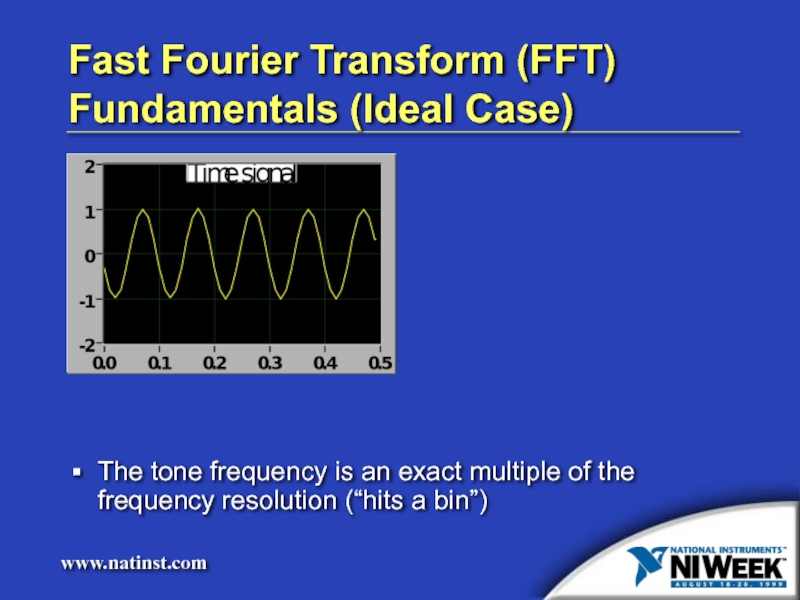
- 6. Fast Fourier Transform (FFT) Fundamentals (Ideal Case)
- 7. FFT Fundamentals (Realistic Case) The tone frequency is not a multiple of the frequency resolution
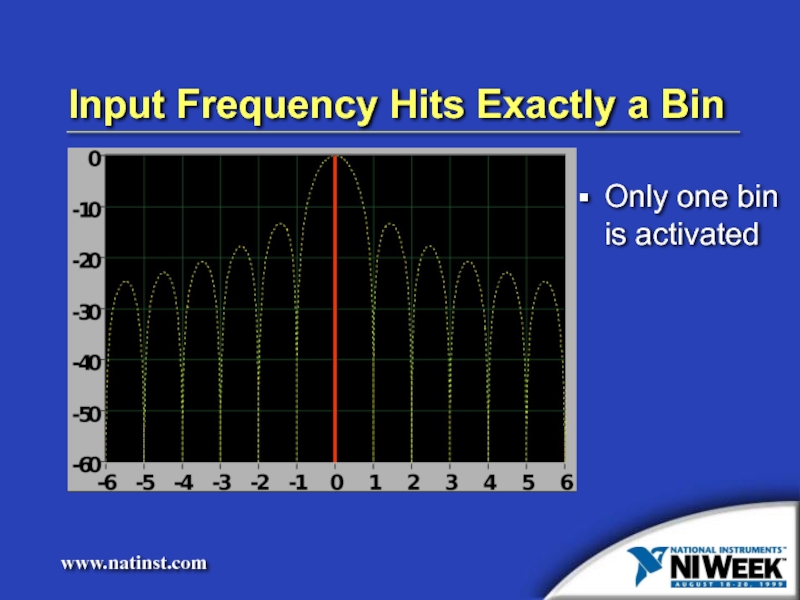
- 8. Input Frequency Hits Exactly a Bin Only one bin is activated
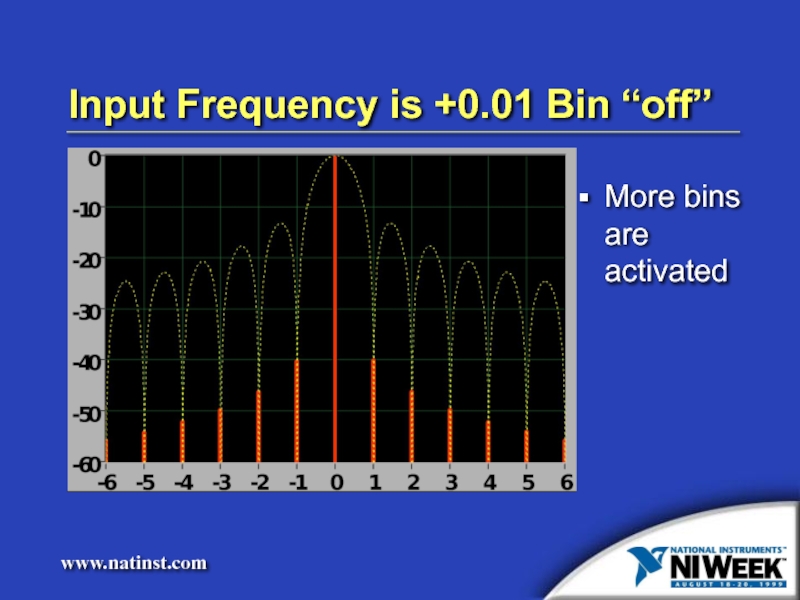
- 9. Input Frequency is +0.01 Bin “off” More bins are activated
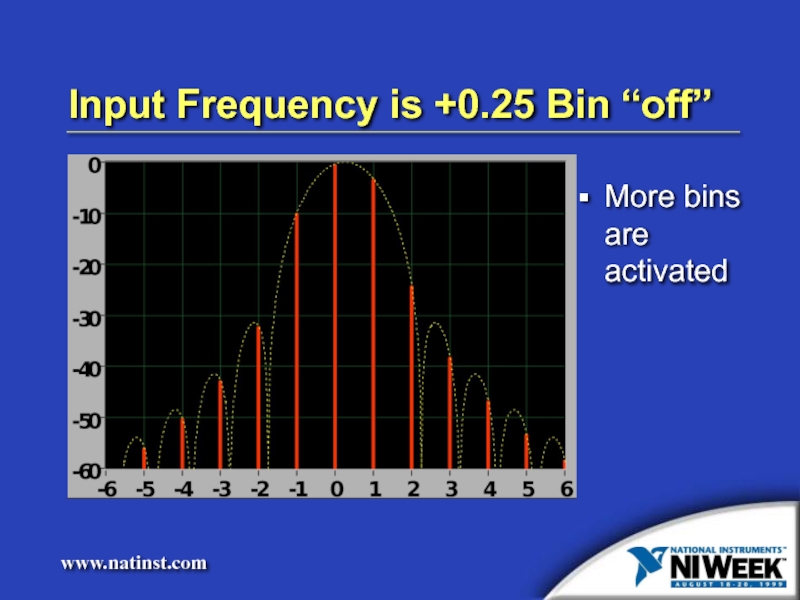
- 10. Input Frequency is +0.25 Bin “off”
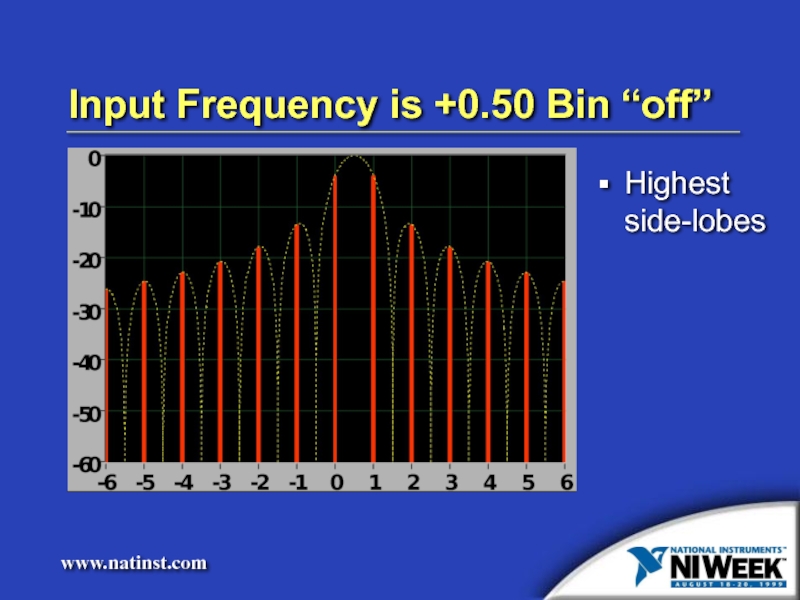
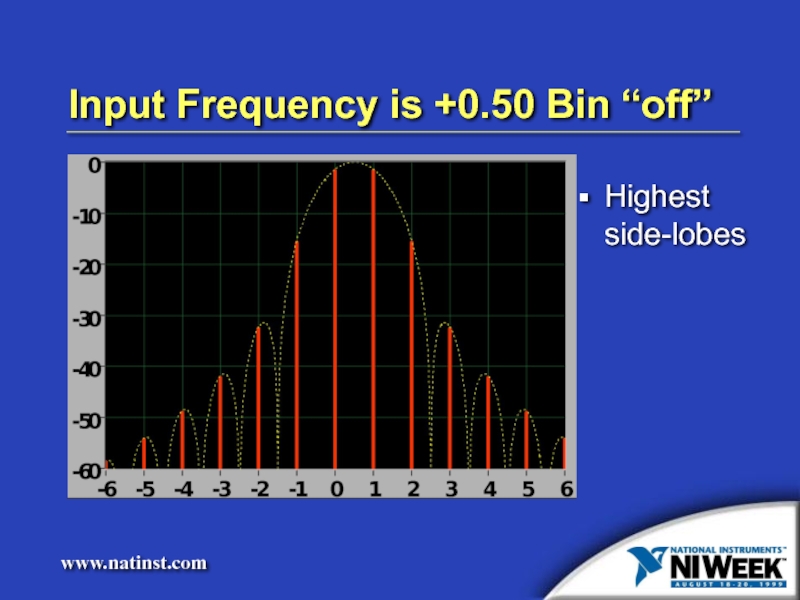
- 11. Input Frequency is +0.50 Bin “off” Highest side-lobes
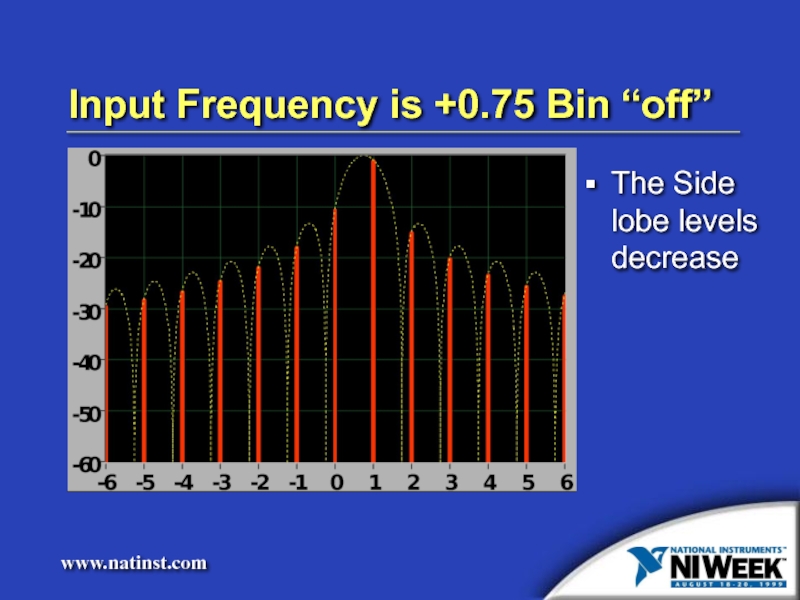
- 12. Input Frequency is +0.75 Bin “off” The Side lobe levels decrease
- 13. Input Frequency is +1.00 Bin “off” Only one bin is activated
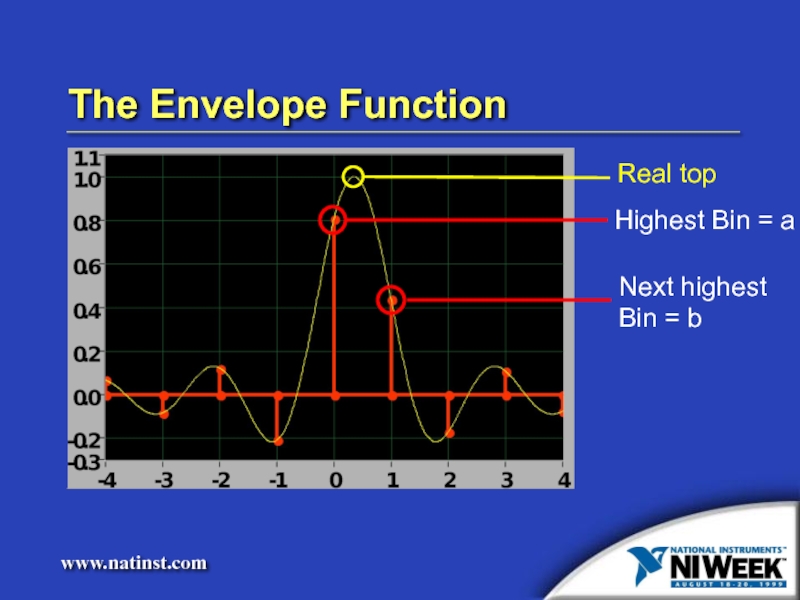
- 14. The Envelope Function
- 15. The Mathematics Envelope function: Bin offset: Real amplitude:
- 16. Demo Amplitude and frequency detection by Sin(x) / x interpolation
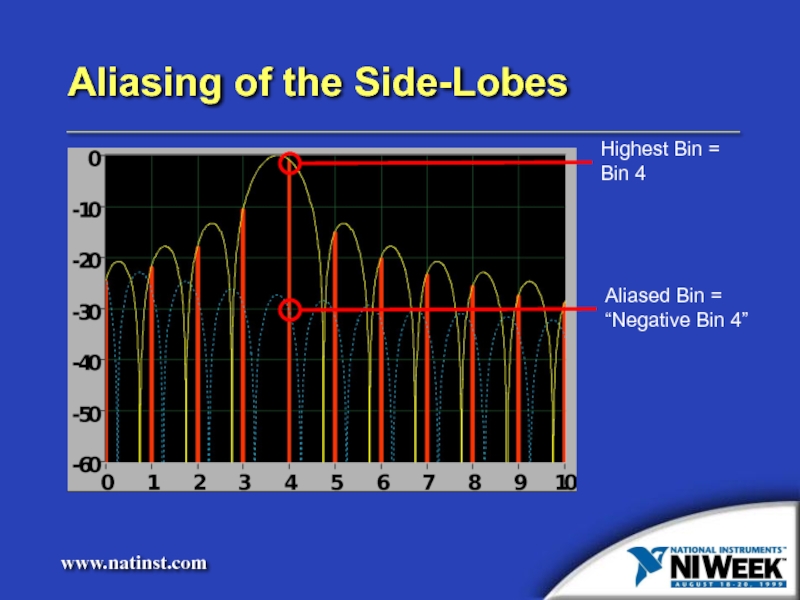
- 17. Aliasing of the Side-Lobes
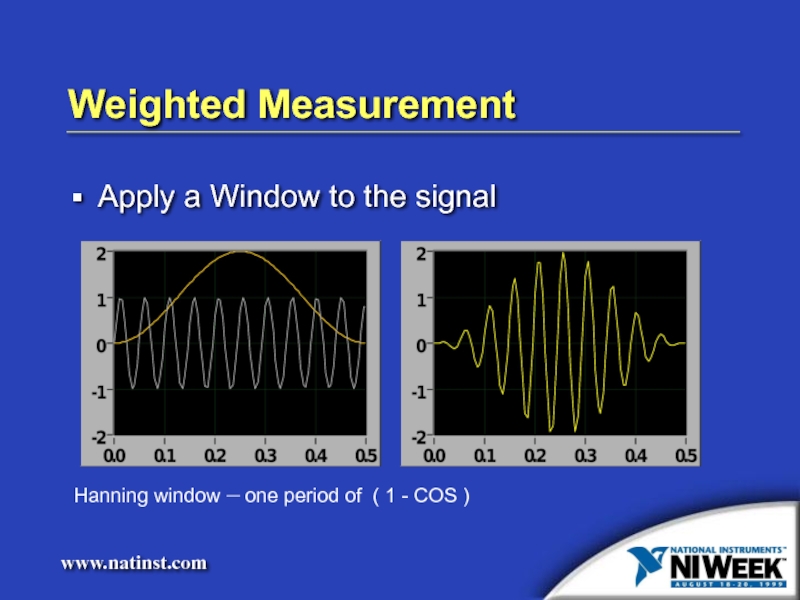
- 18. Weighted Measurement Apply a Window to the signal
- 19. Weighted Spectrum Measurement Apply a Window
- 20. Rectangular and Hanning Windows Side lobes for
- 21. Input Frequency Exactly Hits a Bin Three bins are activated
- 22. Input Frequency is +0.25 Bin “off” More bins are activated
- 23. Input Frequency is +0.50 Bin “off” Highest side-lobes
- 24. Input Frequency is +0.75 Bin “off” The Side lobe levels decrease
- 25. Input Frequency is +1.00 Bin “off” Only three bins activated
- 26. The Mathematics for Hanning ... Envelope: Bin Offset: Amplitude:
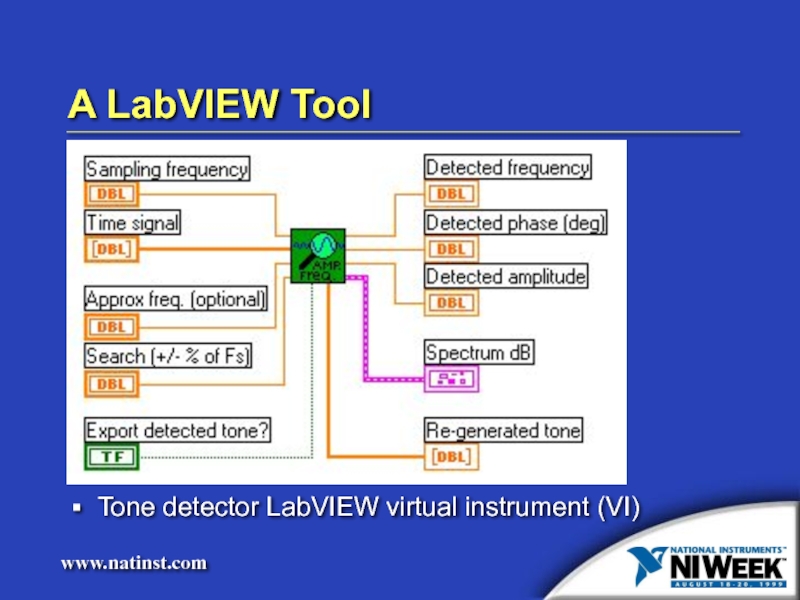
- 27. A LabVIEW Tool Tone detector LabVIEW virtual instrument (VI)
- 28. Demo Amplitude and frequency detection using a
- 29. Frequency Detection Resolution
- 30. Amplitude Detection Resolution
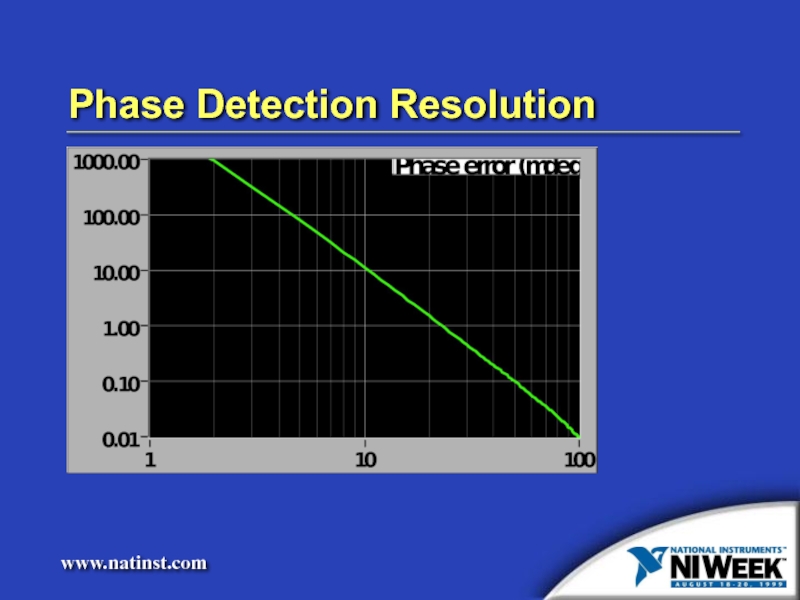
- 31. Phase Detection Resolution
- 32. Conclusions Traditional counters resolve 10 digits in
- 33. Conclusions (Notes Page Only) Traditional Counters Resolve
Слайд 1Fast Frequency and Response Measurements using FFTs
Alain Moriat,
Senior Architect
Fri. 12:45p
Pecan
Слайд 2Accurately Detect a Tone
What is the exact frequency and amplitude
of a tone embedded in a complex signal?
How fast can I perform these measurements?
How accurate are the results?
How fast can I perform these measurements?
How accurate are the results?
Слайд 3Presentation Overview
Why use the frequency domain?
FFT – a short introduction
Frequency interpolation
Improvements
using windowing
Error evaluation
Amplitude/phase response measurements
Demos
Error evaluation
Amplitude/phase response measurements
Demos
Слайд 5Noisy Tone Measurement
Noisy signal
Difficult to measure in the time domain
Noisy signal
spectrum
Easier to measure
Easier to measure
Слайд 6Fast Fourier Transform (FFT) Fundamentals (Ideal Case)
The tone frequency is an
exact multiple of the frequency resolution (“hits a bin”)
Слайд 7FFT Fundamentals (Realistic Case)
The tone frequency is not a multiple of
the frequency resolution
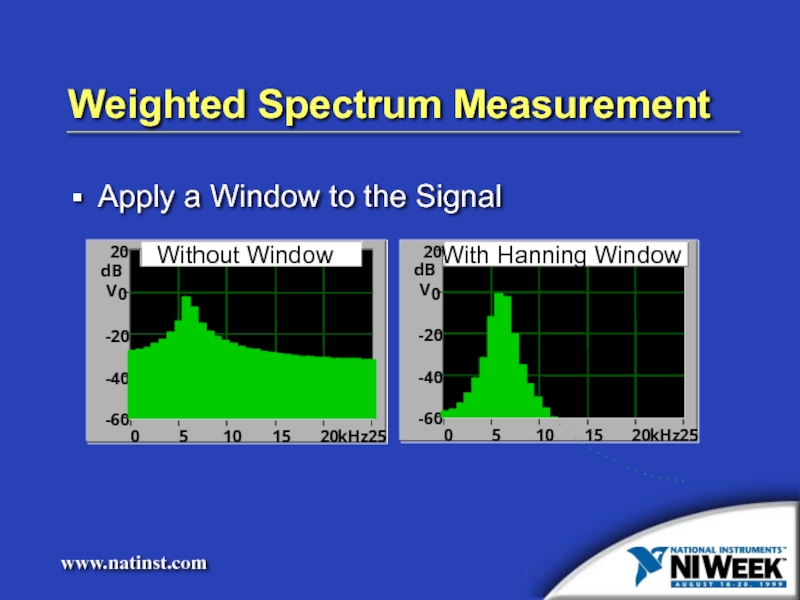
Слайд 19
Weighted Spectrum Measurement
Apply a Window to the Signal
20
-60
-40
-20
0
25
0
5
10
15
20
Without Window
kHz
dBV
20
-60
-40
-20
0
25
0
5
10
15
20
With Hanning Window
kHz
dBV
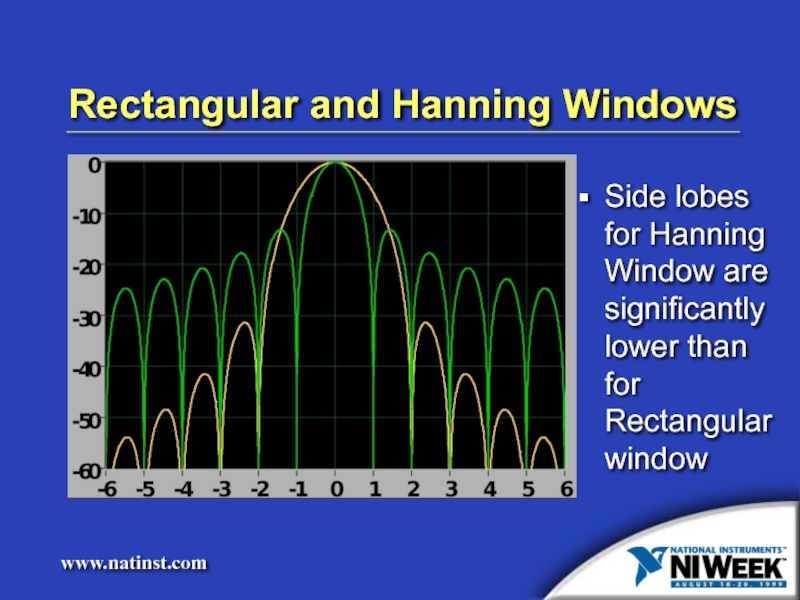
Слайд 20Rectangular and Hanning Windows
Side lobes for Hanning Window are significantly lower
than for Rectangular window
Слайд 28Demo
Amplitude and frequency detection using a Hanning Window (named after Von
Hann)
Real world demo using:
The NI-5411 ARBitrary Waveform Generator
The NI-5911 FLEXible Resolution Oscilloscope
Real world demo using:
The NI-5411 ARBitrary Waveform Generator
The NI-5911 FLEXible Resolution Oscilloscope
Слайд 32Conclusions
Traditional counters resolve 10 digits in one second
FFT techniques can do
this in much less than 100 ms
Another example of 10X for test
Similar improvements apply to amplitude and phase
Another example of 10X for test
Similar improvements apply to amplitude and phase
Слайд 33Conclusions (Notes Page Only)
Traditional Counters Resolve 10 digits in one second
FFT Techniques can do this in much less than 100 ms
Another example of 10X for test
Similar improvements apply to Amplitude and Phase