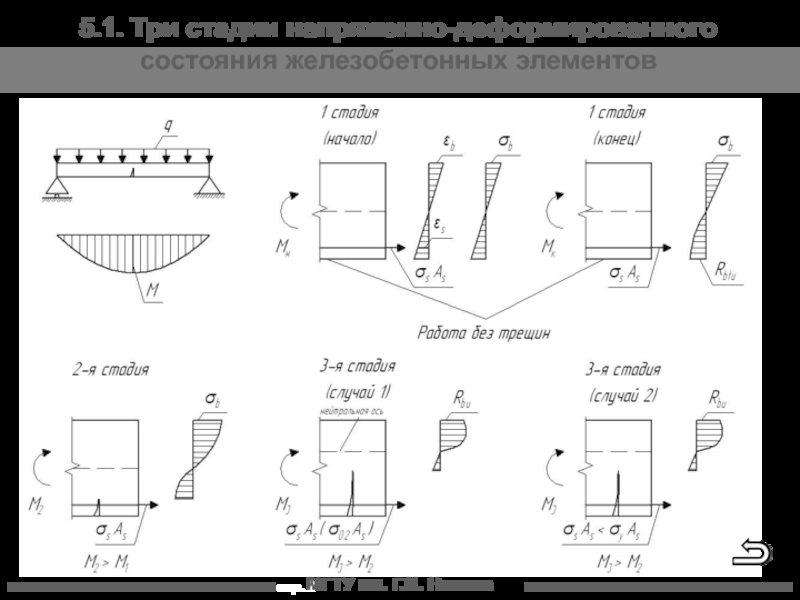
железобетонных элементов
5.2. Метод расчета по предельным состояниям
5.2.1. Две группы предельных состояний
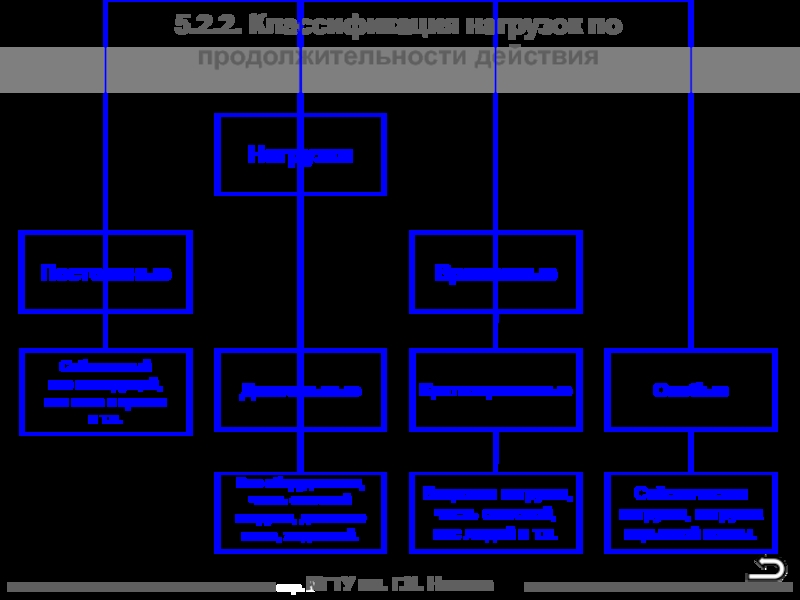
5.2.2. Классификация нагрузок по продолжительности действия
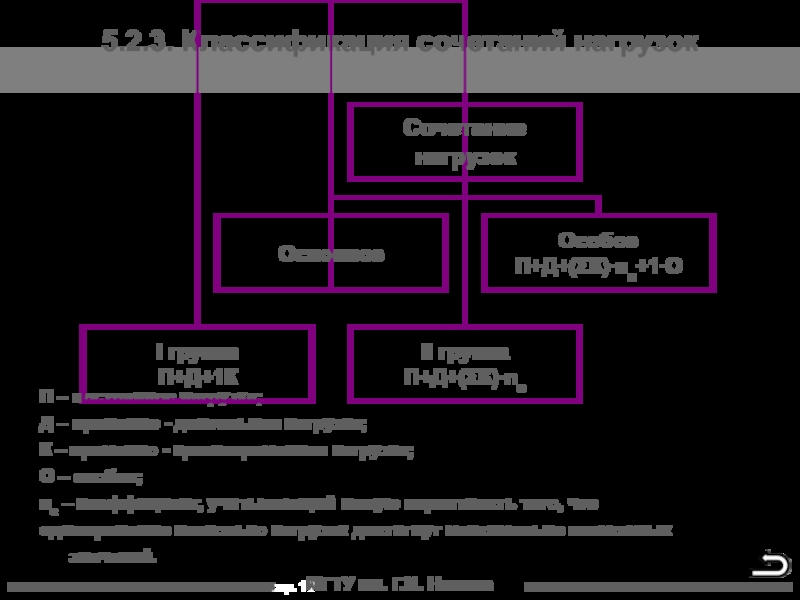
5.2.3. Классификация сочетаний нагрузок
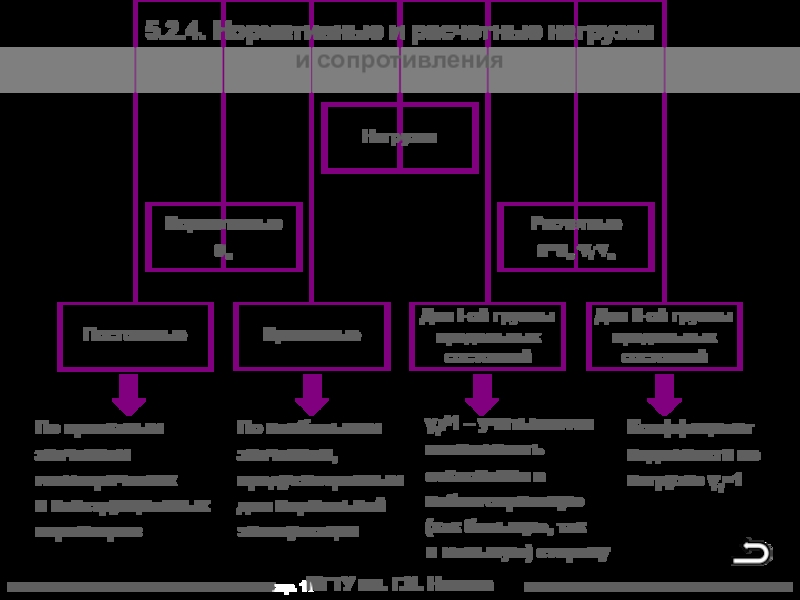
5.2.4. Нормативные и расчетные нагрузки и сопротивления
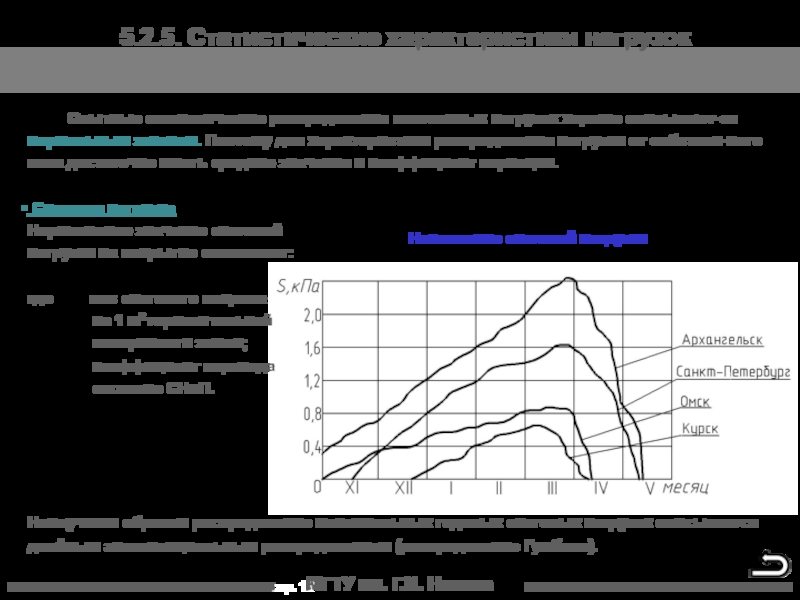
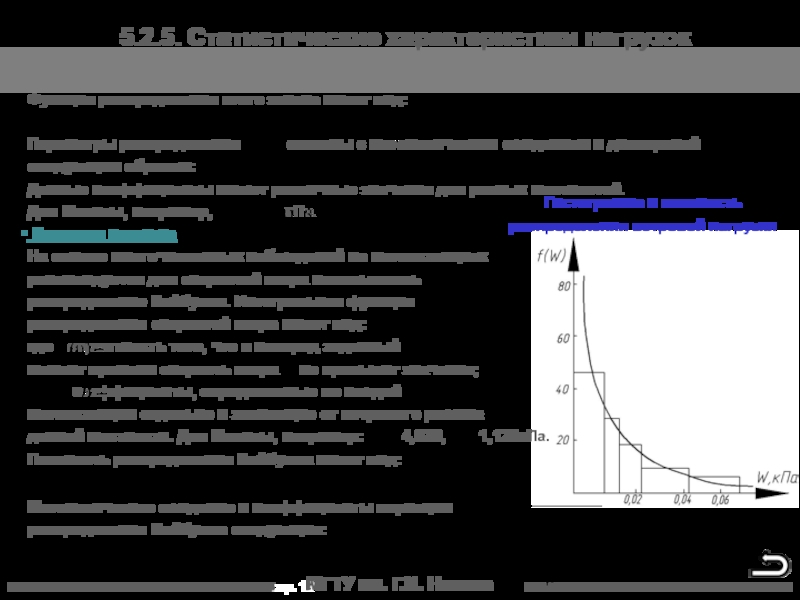
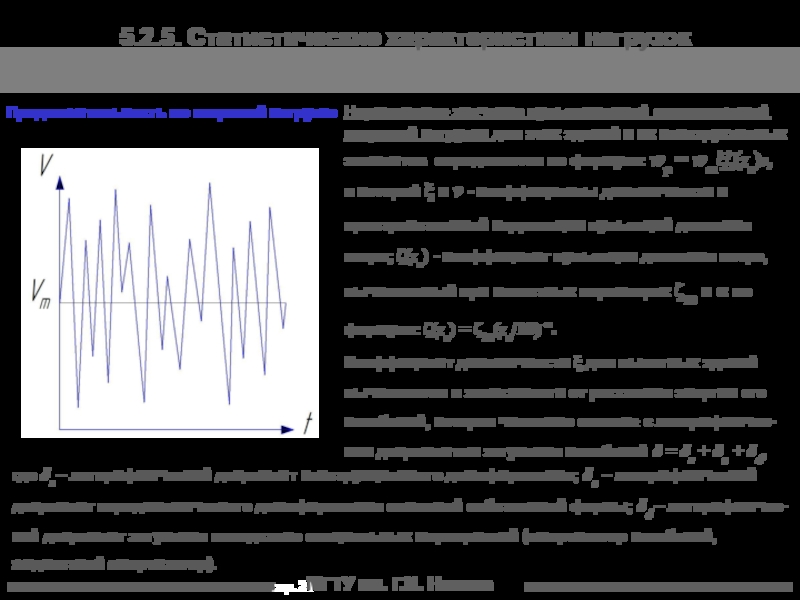
5.2.5. Статистические характеристики нагрузок
5.2.6. Трещиностойкость железобетонных конструкций
5.2.7. Предельные состояния первой и второй групп
5.3. Предварительное напряжение в арматуре
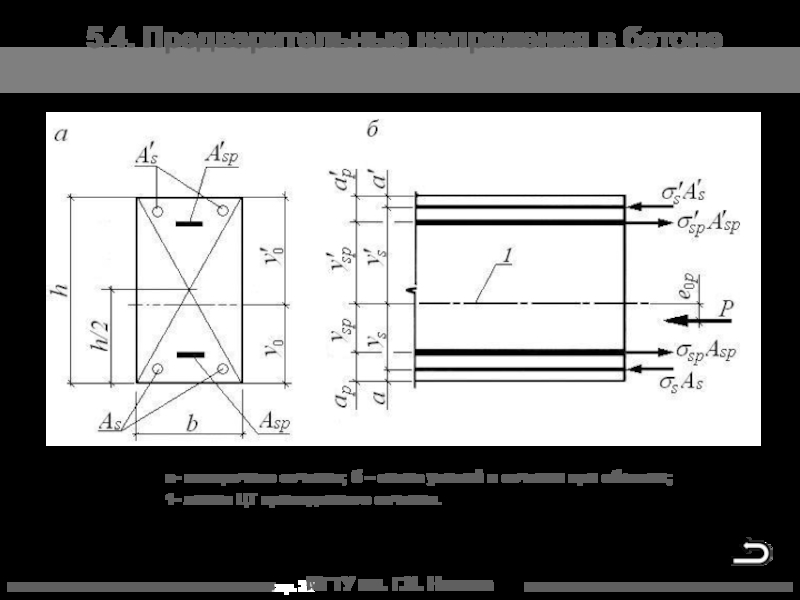
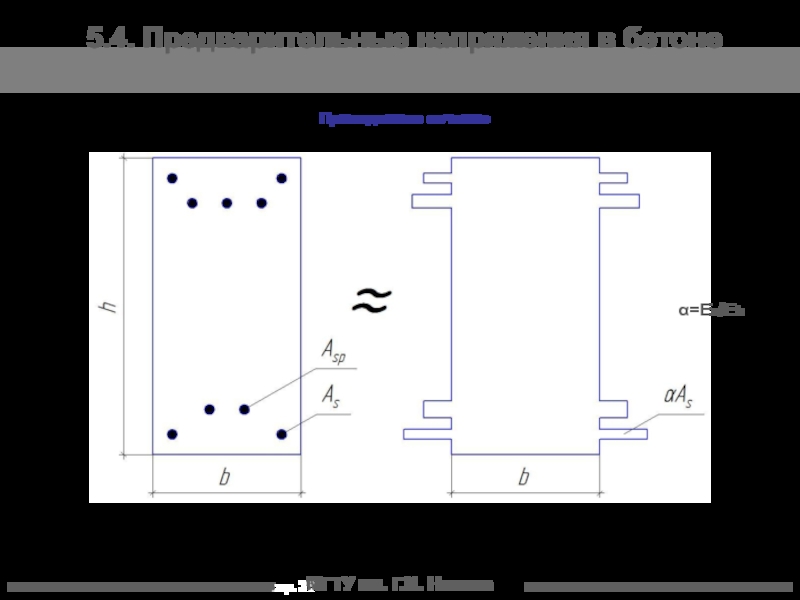
5.4. Предварительные напряжения в бетоне
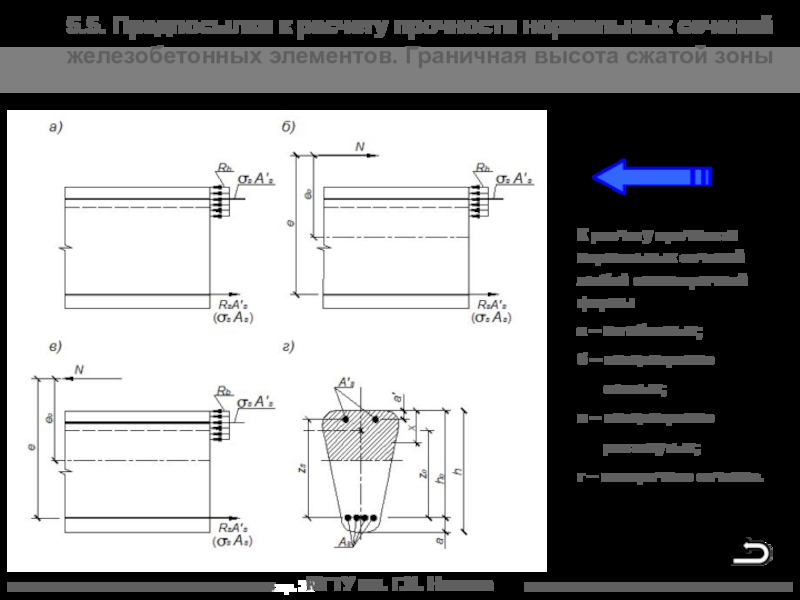
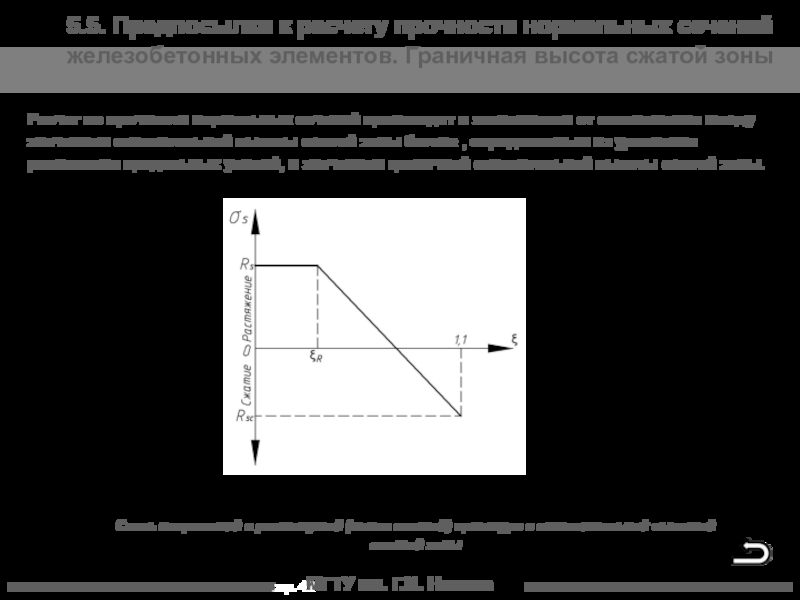
5.5. Предпосылки к расчету прочности нормальных сечений
железобетонных элементов. Граничная высота сжатой зоны
5. Экспериментальные основы и основные положения метода
расчета железобетонных конструкций по предельным состояниям