- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЕГЭ по информатике и ИКТ-2013Часть В презентация
Содержание
- 1. ЕГЭ по информатике и ИКТ-2013Часть В
- 2. В1. У исполнителя Арифметик две команды, которым
- 3. В2. Определите значение переменной c после выполнения
- 4. В2. Определите значение переменной c после выполнения
- 5. В3. Дан фрагмент электронной таблицы. Решение: А2
- 6. В4. Азбука Морзе позволяет кодировать символы для
- 7. В5. Определите, что будет напечатано в результате
- 8. В5. Определите, что будет напечатано в результате
- 9. В6. Алгоритм вычисления значения функции F(n), где
- 10. В7. Запись десятичного числа в системах счисления
- 11. В8. Ниже на четырёх языках записан алгоритм.
- 12. В8. Ниже на четырёх языках записан алгоритм.
- 13. В8. Ниже на четырёх языках записан алгоритм.
- 14. В9. На рисунке – схема дорог, связывающих
- 15. В10. Документ объёмом 20 Мбайт можно передать
- 16. В11. В терминологии сетей TCP/IP маской сети
- 17. В11. IP-адрес узла: 217.19.128.131 Маска: 255.255.192.0
- 18. В11. IP-адрес узла: 217.19.128.131 Маска: 255.255.192.0
- 19. В11. IP-адрес узла: 217.19.128.131 Маска: 255.255.192.0
- 20. В11. IP-адрес узла: 217.19.128.131 Маска: 255.255.192.0
- 21. В12. В языке запросов поискового сервера для
- 22. В13. У исполнителя Удвоитель две команды, которым
- 23. В13. 1. прибавь 1, 2. умножь
- 24. В14. Определите, какое число будет напечатано в
- 25. В14. Определите, какое число будет напечатано в
- 26. В14. Определите, какое число будет напечатано в
- 27. В15. Сколько существует различных наборов значений логических
- 28. В15. (x1 → x2) /\ (x2 →
- 29. В15. (x1 → x2) /\ (x2 →
- 30. В15. (y1 → x1) /\ (y2 →
- 31. В15. (y1 → x1) /\ (y2 →
Слайд 1ЕГЭ по информатике и ИКТ-2013
Часть В
Халиков Ленар Зявдатович, учитель информатики
Муниципальное бюджетное
Слайд 2В1. У исполнителя Арифметик две команды, которым присвоены номера: 1. прибавь 2, 2.
Решение:
Данную задачу проще решать, если начать с конца.
69:3=23 (2)
23-2=21 (1)
21:3=7 (2)
7-2=5 (1)
5-2=3 (1)
В итоге, команда выглядит так: 11212
Ответ: 11212
Слайд 3В2. Определите значение переменной c после выполнения следующего фрагмента программы (записанного
Слайд 4В2. Определите значение переменной c после выполнения следующего фрагмента программы (записанного
Решение:
а = 30
b = 14
a = a – 2*b = 30 – 2 * 14 = 30 – 28 = 2
Условие a > b не выполняется, следовательно
с = b – 2 * a = 14 – 2 * 2 = 14 – 4 = 10
Ответ: 10
Слайд 5В3. Дан фрагмент электронной таблицы.
Решение:
А2 = (B1-A1)/2 = (4-2) / 2
В2 = 2-A1/2 = 2 – 1 = 1 (это два одинаковых участка)
Следовательно, третий участок в два раза больше одного из них
С3 = (C1-A1)*2 – 4 = 2
(С1 – 2) *2 = 6
С1 – 2 = 3
С1 = 5
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2 : С2
соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Ответ: 5
Слайд 6В4. Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая
Решение:
Здесь используется бинарный код (точка и тире)
Используя 4 сигнала, можно закодировать 24=16 символа,
используя 5 сигналов, можно закодировать 25=32 символа.
Следовательно, чтоб закодировать символы, используя код азбуки Морзе длиной не менее четырёх и не более пяти сигналов необходимо 16 + 32 = 48 символов
Ответ: 48
Слайд 7В5. Определите, что будет напечатано в результате выполнения программы (записанной ниже
Слайд 8В5. Определите, что будет напечатано в результате выполнения программы (записанной ниже
Решение:
Чтобы выйти из цикла s должно равняться или быть больше 36.
1) n=n+1=0+1=1
s=s+4=0+4=4
2) n=n+1=1+1=2
s=s+4=4+4=8 и т.д., т.е. получается число, кратное 4. Число 36 делится на 4: 36/4=9
Ответ: 9
Слайд 9В6. Алгоритм вычисления значения функции F(n), где n – натуральное число,
Решение:
F(1) = 1
F(n) = F(n–1) * n, при n >1
F(5) - ?
F(2) = F(2–1) * 2 = 1*2=2
F(3) = F(3–1) * 3 = 2*3=6
F(4) = F(4–1) * 4 = 6*4=24
F(5) = F(5–1) * 5 = 24*5=120
Ответ: 120
Слайд 10В7. Запись десятичного числа в системах счисления с основаниями 3 и
Решение:
Т.к. последнее число 0, то десятичное число должно одновременно цело делиться на 3 и 5. Минимальное натуральное число, которое удовлетворяет этому условию – это 15
Ответ: 15
Слайд 11В8. Ниже на четырёх языках записан алгоритм. Получив на вход число
Слайд 12В8. Ниже на четырёх языках записан алгоритм. Получив на вход число
«a» – должно равняться 2, а «b» – 21.
Значение «а» увеличивается на единицу, т.е. цикл будет выполнятся 2 раза и каждый раз отбрасываться по одной цифре, поэтому входное значение Х будет двузначным.
Число 21 можно получить произведением 3 на 7, поэтому при div должно получиться 3, а при mod – 7.
Решение:
mod – оператор нахождения остатка при делении двух целых чисел. X mod 10 – при делении Х на 10 получается самая правая цифра, младший разряд.
div – оператор нахождения целой части при делении двух целых чисел. X div 10 – при делении Х на 10 получается самая левая цифра, старший разряд.
Слайд 13В8. Ниже на четырёх языках записан алгоритм. Получив на вход число
x=0, следовательно, выходим из цикла. Проверяем, a=2, b=21, подходит. В итоге значения для х будет 37.
Решение:
Ответ: 37
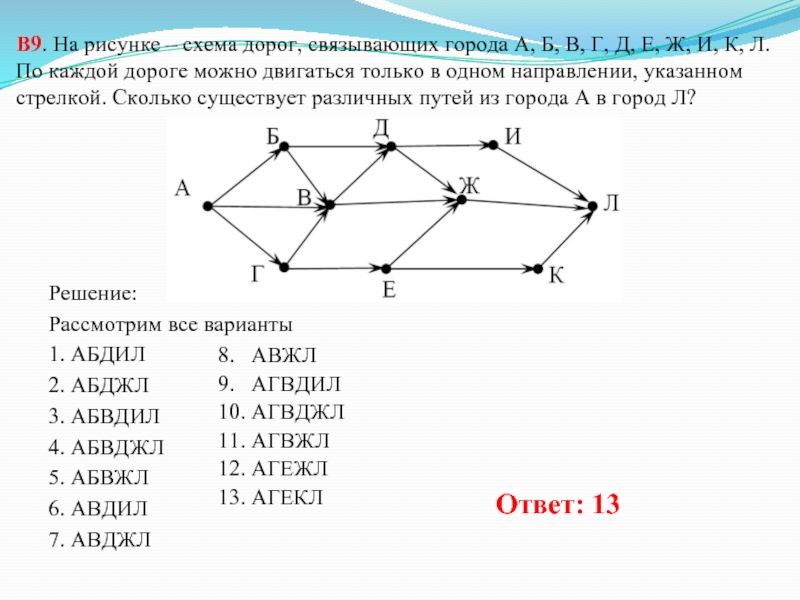
Слайд 14В9. На рисунке – схема дорог, связывающих города А, Б, В,
Решение:
Рассмотрим все варианты
1. АБДИЛ
2. АБДЖЛ
3. АБВДИЛ
4. АБВДЖЛ
5. АБВЖЛ
6. АВДИЛ
7. АВДЖЛ
8. АВЖЛ
9. АГВДИЛ
10. АГВДЖЛ
11. АГВЖЛ
12. АГЕЖЛ
13. АГЕКЛ
Ответ: 13
Слайд 15В10. Документ объёмом 20 Мбайт можно передать с одного компьютера на
Ответ: А122
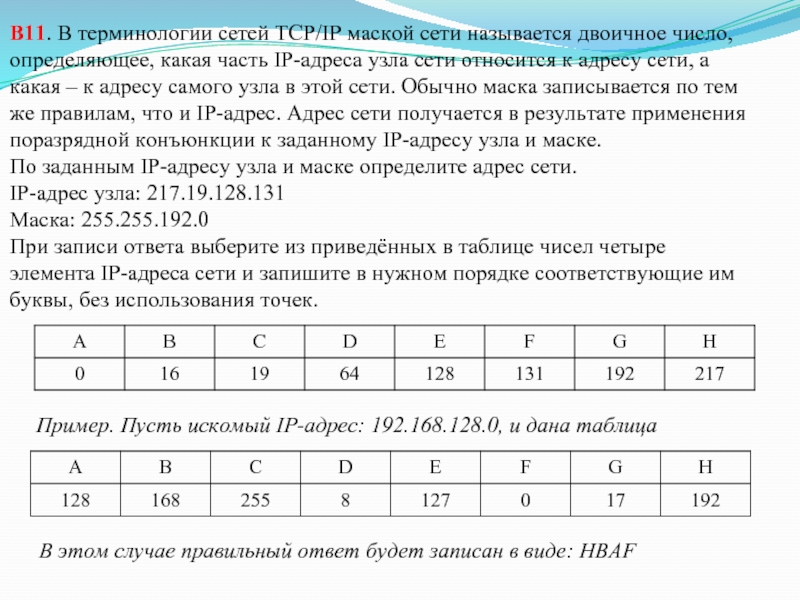
Слайд 16В11. В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая
Пример. Пусть искомый IP-адрес: 192.168.128.0, и дана таблица
В этом случае правильный ответ будет записан в виде: HBAF
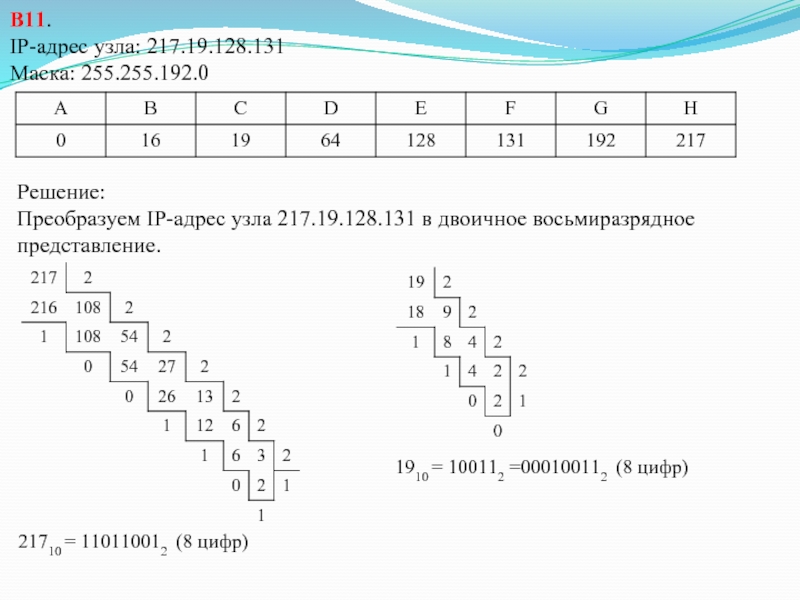
Слайд 17В11.
IP-адрес узла: 217.19.128.131
Маска: 255.255.192.0
Решение:
Преобразуем IP-адрес узла 217.19.128.131 в двоичное восьмиразрядное
21710 = 110110012 (8 цифр)
1910 = 100112 =000100112 (8 цифр)
Слайд 18В11.
IP-адрес узла: 217.19.128.131
Маска: 255.255.192.0
Решение:
Преобразуем IP-адрес узла 217.19.128.131 в двоичное восьмиразрядное
12810 = 100000002 (8 цифр)
13110 =100000112 (8 цифр)
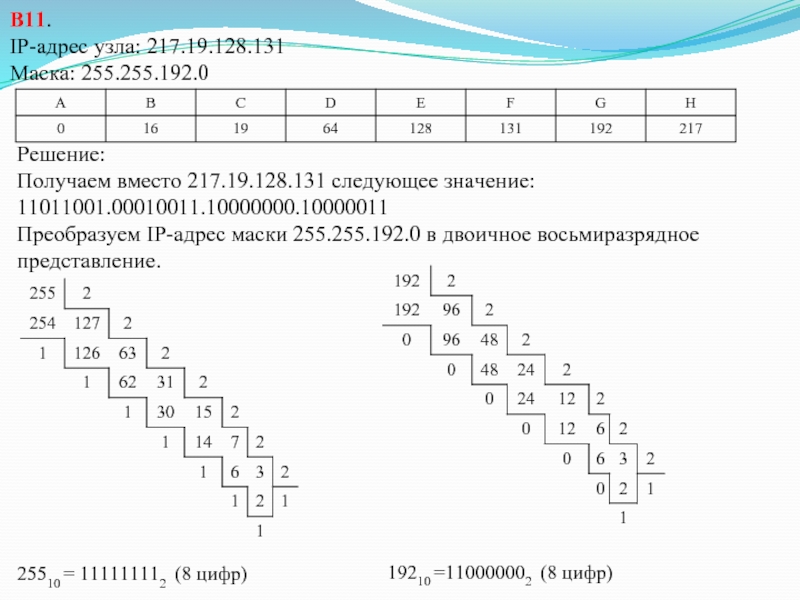
Слайд 19В11.
IP-адрес узла: 217.19.128.131
Маска: 255.255.192.0
Решение:
Получаем вместо 217.19.128.131 следующее значение:
11011001.00010011.10000000.10000011
Преобразуем IP-адрес маски
25510 = 111111112 (8 цифр)
19210 =110000002 (8 цифр)
Слайд 20В11.
IP-адрес узла: 217.19.128.131
Маска: 255.255.192.0
Решение:
Получаем вместо 217.19.128.131 следующее значение:
11011001.00010011.10000000.10000011
Получаем вместо 255.255.192.0
11111111.11111111.11000000.00000000
Далее производим поразрядное умножение (конъюнкцию)
1 1 0 1 1 0 0 1. 0 0 0 1 0 0 1 1. 1 0 0 0 0 0 0 0. 1 0 0 0 0 0 1 1 (IP-адрес узла)
1 1 1 1 1 1 1 1. 1 1 1 1 1 1 1 1. 1 1 0 0 0 0 0 0. 0 0 0 0 0 0 0 0 (Маска)
1 1 0 1 1 0 0 1. 0 0 0 1 0 0 1 1. 1 0 0 0 0 0 0 0. 0 0 0 0 0 0 0 0 (IP-адрес сети)
Полученные двоичные числа преобразуем в десятичный код.
7 6 5 4 3 2 1 0
1 1 0 1 1 0 0 12 = 1*27+1*26+0*25+1*24+1*23+0*22+0*21+1*20=128+64+16+8+1=21710
7 6 5 4 3 2 1 0
0 0 0 1 0 0 1 12 = 0*27+0*26+0*25+1*24+0*23+0*22+1*21+1*20=16+2+1=1910
7 6 5 4 3 2 1 0
1 0 0 0 0 0 0 02 = 1*27=12810
0 0 0 0 0 0 0 02 = 010
В итоге получаем, 217.19.128.0 . Это соответствует в таблице HCEA
Ответ: HCEA
Слайд 21В12. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется
Решение:
Необходимо использовать круги Эйлера.
Для Фрегат | Эсминец будет X+Y+Z=3400
Для Фрегат & Эсминец будет Y=900
Для Фрегат будет X+Y=2100
Для Эсминец будет Y+Z=?
Из первого уравнения выражаем Z и вместо (X+Y) подставляем 2100:
Z=3400-(X+Y)=3400-2100=1300
Далее Y+Z=900+1300=2200
X Y
Z
Фрегат
Эсминец
Ответ: 2200
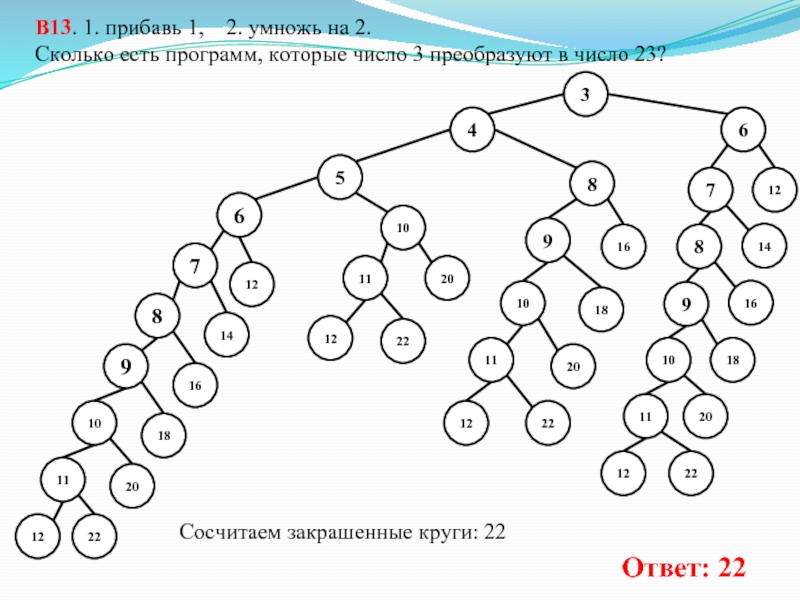
Слайд 22В13. У исполнителя Удвоитель две команды, которым присвоены номера: 1. прибавь 1, 2.
Решение:
Надо использовать древо. Левая ветвь – прибавить 1, правая ветвь – умножить на 2.
Когда число получится больше 11, дальше правую ветвь можно и не продолжать, т.к. при умножении этого числа на 2, мы получим число, превосходящее 23. Но будет левая ветвь, и она рано или поздно достигнет числа 23 (по +1).
Слайд 23В13. 1. прибавь 1, 2. умножь на 2. Сколько есть программ,
3
6
4
12
7
5
8
8
14
9
10
11
12
16
18
22
20
16
18
20
22
12
11
10
9
10
20
11
22
12
12
14
16
18
20
22
12
11
10
9
8
7
6
Сосчитаем закрашенные круги: 22
Ответ: 22
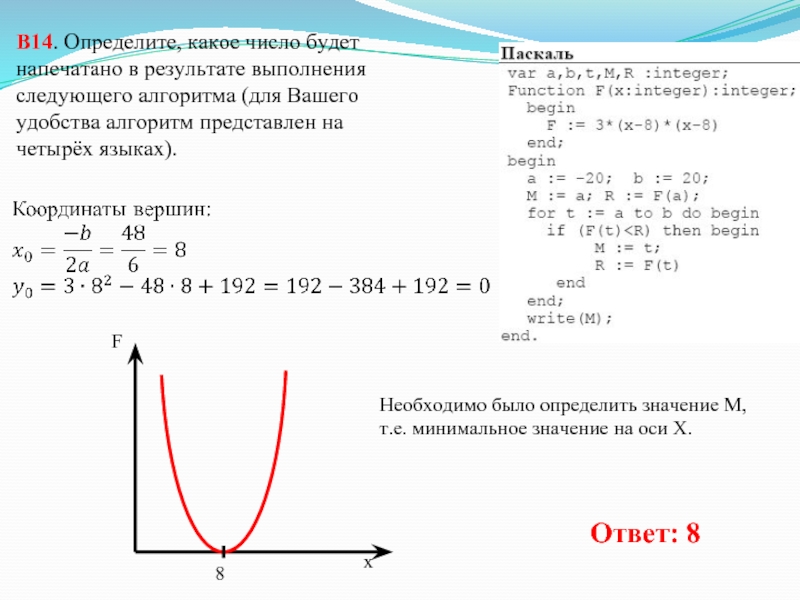
Слайд 24В14. Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для
Слайд 25В14. Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для
Решение: F = 3*(x-8)*(x-8) = 3*(x-8)2 = 3*(x2-16x+64) = 3x2-48x+192
a – левая граница отрезка,
b – правая граница отрезка,
t – счетчик, проходящий отрезок [a;b] с шагом 1,
F(t) – значение функция F в заданной точке,
М – значение, при котором функция F принимает минимальное значение на оси х (т.к. F(t)
F – квадратичное уравнение, где a=3, b=-48, c=192
Графиком является парабола, у которой ветви направлены вверх, т.к. а=4 число положительное.
Слайд 26В14. Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для
F
x
8
Необходимо было определить значение М, т.е. минимальное значение на оси Х.
Ответ: 8
Слайд 27В15. Сколько существует различных наборов значений логических переменных x1, x2, x3,
Решение:
28 = 256 вариантов
Рассмотрим первое условие
(x1 → x2) /\ (x2 → x3) /\ (x3 → x4) = 1
Если (x1 → x2) = 0, условие выполнятся не будет, т.е. x1=1, x2=0
Если (x2 → x3) = 0, условие выполнятся не будет, т.е. x2=1, x3=0
Если (x3 → x4) = 0, условие выполнятся не будет, т.е. x3=1, x4=0
Слайд 28В15. (x1 → x2) /\ (x2 → x3) /\ (x3 →
Решение:
Построим часть таблицы. В скобках укажем сколько нулей или единиц будет в столбце
Если (x1 → x2) = 0, условие выполнятся не будет, т.е. x1=1, x2=0
Если (x2 → x3) = 0, условие выполнятся не будет, т.е. x2=1, x3=0
Если (x3 → x4) = 0, условие выполнятся не будет, т.е. x3=1, x4=0
Закрашенные строки не удовлетворяют первому условию, следовательно 256-16-32-16-64-32-16=80
Остается 80 вариантов
Слайд 29В15. (x1 → x2) /\ (x2 → x3) /\ (x3 →
Решение:
Рассмотрим 2 условие
(¬y1 \/ y2) /\ (¬y2 \/ y3) /\ (¬y3 \/ y4) = 1
Для начала отдельно запишем части не закрашенных строк по отдельности («внутри» х4)
Если (¬y1 \/ y2) = 0, условие выполнятся не будет, т.е. у1=1, у2=0
Если (¬y2 \/ y3) = 0, условие выполнятся не будет, т.е. у2=1, у3=0
Если (¬y3 \/ y4) = 0, условие выполнятся не будет, т.е. у3=1, у4=0
В итоге еще 11 строк не удовлетворяют условию
Остается 80-11=69 вариантов
Остальные 4 не закрашенные строки из х4 аналогичны, следовательно
Остается 69-11-11-11-11=25 вариантов
Слайд 30В15. (y1 → x1) /\ (y2 → x2) /\ (y3 →
Решение:
Рассмотрим 3 условие
(y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) =1
Будем использовать часть таблицы (для удобства закрашенные участки сохраним)
Если (y1 → x1)=0, условие выполнятся не будет, т.е. у1=1, x1=0
Пятую не закрашенную строку из х4 рассматривать не будем, т.к. там x1=1
Здесь есть один вариант, при котором у1=1, x1=0
Остается 25-1=24 варианта
Аналогично из второй, третьей и четвертой не закрашенной строки х4
Остается 24-1-1-1=21 варианта
Если (y2 → x2)=0, условие выполнятся не будет, т.е. у2=1, x2=0
Четвертую и пятую не закрашенную строку из х4 рассматривать не будем, т.к. там x2=1
Здесь есть один вариант, при котором у2=1, x2=0
Остается 21-1=20 варианта
Аналогично из второй и третьей не закрашенной строки х4
Остается 20-1-1=18 вариантов
Слайд 31В15. (y1 → x1) /\ (y2 → x2) /\ (y3 →
Решение:
Рассмотрим 3 условие
(y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) =1
Будем использовать часть таблицы (для удобства закрашенные участки сохраним)
Если (y3 → x3)=0, условие выполнятся не будет, т.е. у3=1, x3=0
Третью, четвертую и пятую не закрашенную строку из х4 рассматривать не будем, т.к. там x3=1
Здесь есть один вариант, при котором у3=1, x3=0
Остается 18-1=17 вариантов
Аналогично из второй не закрашенной строки х4
Остается 17-1=16 вариантов
Если (y4 → x4)=0, условие выполнятся не будет, т.е. у4=1, x4=0
Вторую, третью, четвертую и пятую не закрашенную строку из х4 рассматривать не будем, т.к. там x4=1
Здесь есть один вариант, при котором у4=1, x4=0
Остается 16-1=15 вариантов
Ответ: 15