Дисциплина Компьютерное обеспечение инженерных задач презентация

– 2
Семестр – 4
Форма контроля – зачет
Лекции – 16 часов
Лабораторные работы – 14 часов

Целью настоящего курса – дать студенту знания и практические навыки в области организации вычислений при решении инженерных задач с использованием современных математических пакетов (MATLAB).

Автор курса

к.т.н., доцент Красов Андрей Владимирович
директор УИЦ ИТТ, доцент каф. ИБТС
Куратор специальности 201800 «Защищенные системы связи»

«Компьютерное обеспечение инженерных задач» к.т.н., доцент Красов А.В.

компьютерных классах УИЦ ИТТ,
расположенных в учебном корпусе №2 СПбГУТ по адресу наб.р. Мойка д.65.
Аудитории № 42, 43 и 48.
Материалы к занятиям представлены на сайте
в разделе «Кафедра ИБТС \ Материалы к занятиям»

www.mts-sut.spb.ru

задач в среде MatLAB

Краткая характеристика развития науки и потребностей в инженерных расчетах
Первые упоминания, материально сохранившиеся свидетельства и описания научных методик, применения математических моделей и моделирования встречаются еще в древнем мире.
О математических достижениях вавилонской, австрийской цивилизаций сведений сохранилось крайне мало. В III тысячелетии до нашей эры в долине рек Тигра и Ефрата возникло, наверное, древнейшее государство, в котором активно использовались математические знания.
Шумеры использовали 12-и ричную и 60-и ричную позиционную систему счисления, специально ориентированную на астрономические расчеты.
Вавилоняне знали теорему Пифагора, знали очень точно значение главного иррационального числа -  корня из 2, вычисляли квадраты и квадратные корни, кубы и кубические корни, умели решать системы уравнений и квадратные уравнения. Шумеро-вавилонская математика была на голову выше египетской.

Рис. 1.1. Древние шумеры и дошедшая до нас глиняная табличка содержащая математические расчеты

египетские источники II-го тысячелетия до н.э. математического содержания: папирус Ринда (1680 г. до н.э., Британский музей) и Московский папирус.
Они содержат решение отдельных задач, встречающихся в практике, математические вычисления, вычисления площадей и объемов.

Рис. 1.2. Папирус Ринда (1680 г. до н.э., Британский музей)

Математические знания широко использовались в древнем Египте при строительстве пирамид.

Рис.1.3. Использование рычага при строительстве пирамид

теоремы Пифагора и применения орудий Архимеда

Значительно больше сведений сохранилось об уроне развития математики в эпоху древней Греции, хотя нужно отметить, что большая часть знаний шумеро-вавилонской и даже египетской цивилизаций оказались утраченными.
Применение пращи и лука, баллисты требовало осознание зависимости между дальностью полета и силой броска. Мореплавание стимулировало развитие той же астрономии для координации во времени и пространстве, техники строительства судов, гидростатики и многого другого. Торговля способствовала распространению математических и технических знаний.
Появляются первые научные школы, как средство передачи знаний.

В этот период складывается основа последующей восточно-европейской и западноевропейской науки. К этому периоду относятся первые описания применения математических экспериментов, моделирования.
Уже в эту эпоху происходит разделение на материальные и математические модели. Наиболее характерной чертой является применение материальных моделей 1:1. Например, корона Архимеда, метательные орудия.
Математические расчеты применялись только тогда, когда построить модель не было возможности.

Рис. 1.5. Предполагаемый вид одного из гигантских кораблей древности, в строительстве которого принимал участие Архимед.

Применение математических вычислений в используемой тогда непозиционной системе
счисления (позже названную римской системой счисления) было очень трудной задачей. Даже много
веков спустя, в средневековой Европе. Умножение чисел в свою программу мог включить только один
Болонский университет. Для изучения этой операции в него ехали со всей средневековой Европы. Это
было вызвано наследием пиренейских стран от многочисленных войн и контактов с маврами. Арабский
мир в этот период значительно опережал измученную инквизицией Европу.

Рис. 1.6. Шведский фрегат Ваза 1628 г.

Подтверждением правильности, в том
числе и инженерных расчетов, служили
ссылки на библию, священные тексты и
мнения высочайших особ. Например, во
время расследования катастрофы
шведского фрегата «Ваза»,
перевернувшегося на рейде из за огромной
перегрузки артиллерией, его строителя
попросили обосновать составленные им
пропорции корабля. Его ответ был такой
«пропорции утвердил король», и он был
признан правильным, ни какие расчеты
больше не проверялись.

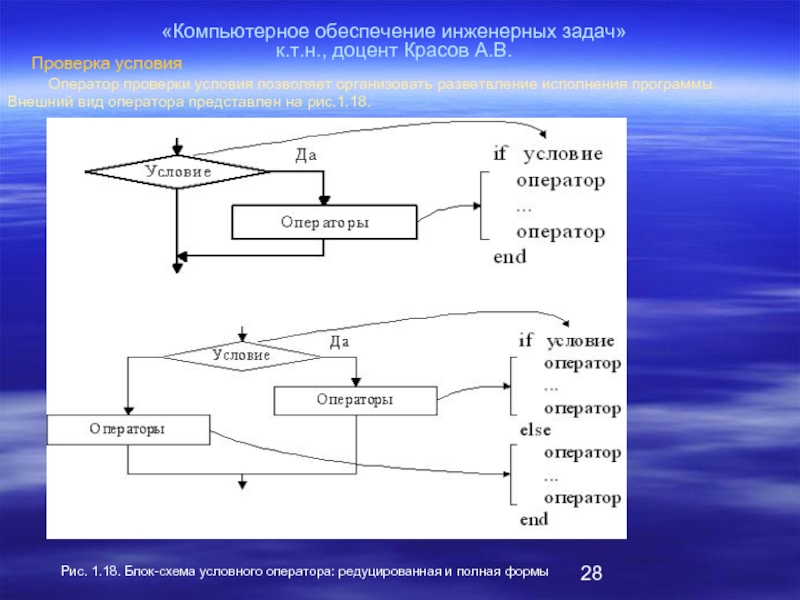
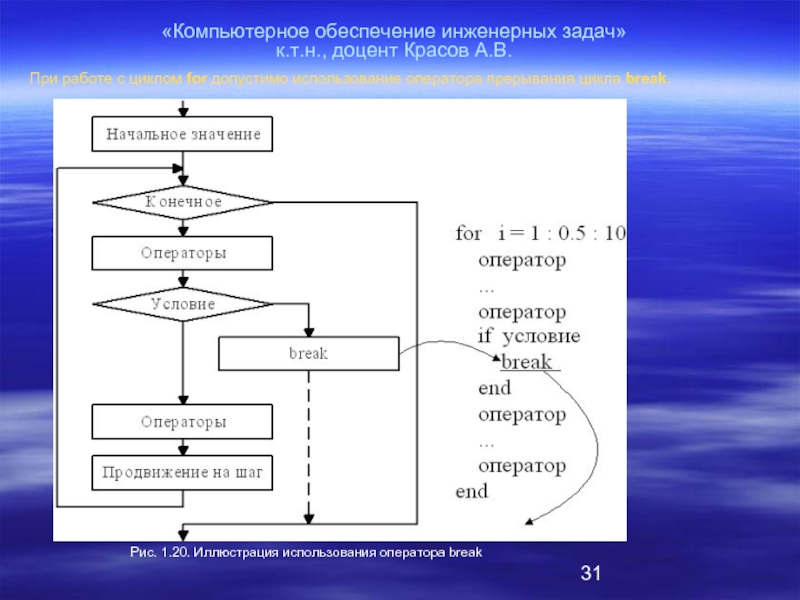
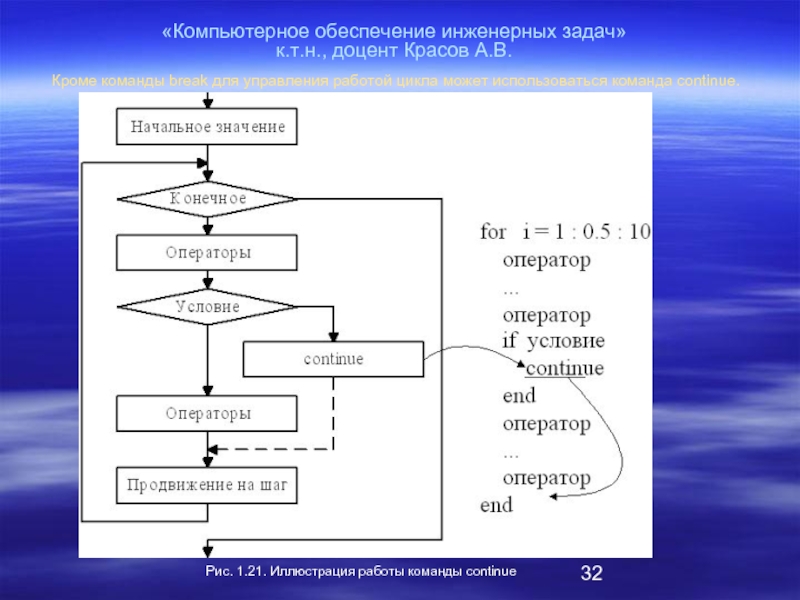
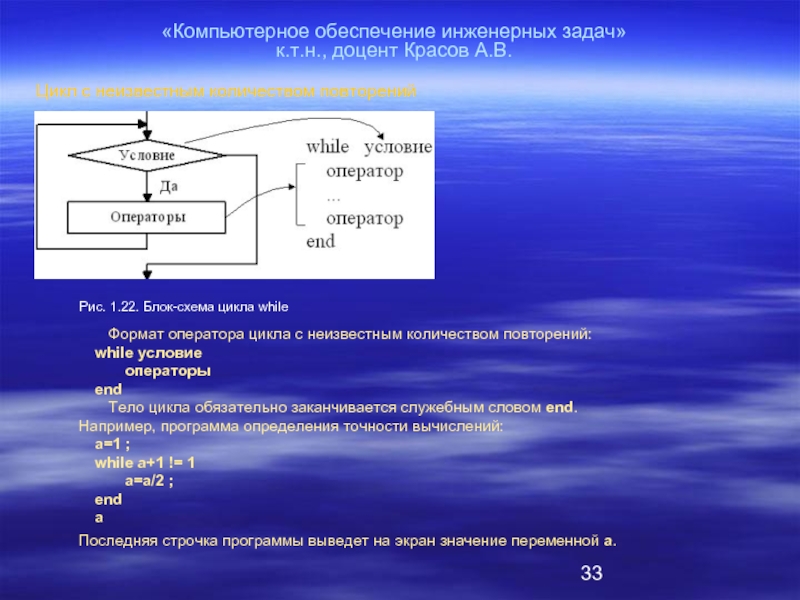
развитие общества вызвало противоречие между потребностями феодальной власти в развитии в первую очередь фортификационных наук, мореплавания, астрономии, торговли, и реакционного отношения церкви к развитию других направлений науки не связанных с христианством.
Но поток золота от торговли с востоком, в первую очередь с Индией, перевесил доводы церкви. В первую очередь Италия, в следствии ее географического положения, особенно Генуэзская и Венецианские республики, затем Португалия и Испания, все шире стали возрождать античные знания, перенимать знания Арабского мира.
Для этого им нужны были более совершенные знания в области мореплавания, кораблестроения, астрономии математики.

Рис. 1.7. Постройка кораблей с заранее прорезанными пушечным портами, это предполагает расчет осадки корабля до его спуска на воду

Первый серьезный результат был достигнут математиком Эйлером, создавшим первую теорию проектирования корабля. Он успешно решил задачу вставшую перед Архимедом, и до сих пор мы пользуемся его формулам численного интегрирования.
Практически все применяемые методы математических расчетов были разработаны до 20 века. Можно назвать методы: Эйлер-1730 год, Крамер, Гаус-1840 год, Якоби-1850 год.

Но отсутствие средств автоматизации расчетов сдерживали круг применяемых задач на практике. Наиболее сложные эксперименты, связанные с судостроением, проводились по прежнему на натуральных объектах.
Так, например, выбор колеса или винта, типа паровых машин.

Рис. 1.8. Натурный эксперимент: выбор что лучше гребное колесо или винт

появились опытные бассейны, начались эксперименты с моделями. Например, опытный бассейн в Петербурге, где выбирались оптимальные обводы кораблей. В этих бассейнах проигрывались различные ситуации. Например, в фильме о катастрофе Титаника на модели проигрывались различные сценарии действий и возможные последствия. Примерно такие же эксперименты ставил в конце прошлого века адмирал С.О. Макаров, с моделью английского броненосца Виктория, катастрофа которого наделала не меньше шума, чем гибель лайнера Титаник.

Рис.1.9. Иллюстрация принципа исследования модели корабля в опытном бассейне

Более сложные задачи - сравнение
двигателей, шагов винтов проявившиеся при
создании турбины Патерсона, поставили
актуально вопрос о адекватности модели и
оригинала. Этот вопрос остро стоит и для
математических моделей.

Аналогичный принцип используется для исследования моделей самолетов в аэродинамической
трубе. Так же определяли оптимальное расположение пропускных ворот, для комплекса защитных
сооружений Ленинграда от наводнений.

Рис. 1.10. Иллюстрация продувки модели самолета в аэродинамической трубе

из решений проблемы расчетов стали аналоговые вычислительные машины. Принцип аналогичен весам, на одну половину балансной схемы устанавливали блок, повторяющий поведение исследуемого объекта, но вторую половину устанавливались эталоны.

Рис.1.11. Аналоговая вычислительная машина

Применение математического моделирования сильно сдерживалось ресурсами ЭВМ. До 1980-х годов активно развивались методы позволяющие по упрощенным и свернутым моделям получить оценки тех или иных параметров или характеристик. Полные методы решения этих задач были известны еще с середины XIX века, но на практике редко ими пользовались для систем выше 3-4-го порядков из-за слишком больших затрат времени

средства MatLAB для работы с линейными и нелинейными моделями;
формулы численного интегрирования и дифференцирования и особенности их применения при организации вычислений;
определение жестких систем и вызванные проявлением жестких составляющих движений проблемы при организации вычислений;
итерационные методы решения уравнений;
явные и неявные методы решения систем дифференциальных уравнений;
алгоритмы анализа топологии моделей;
основные принципы положенные в основу оптимизации;
фундаментальные принципы системного подхода при построении моделей (неизбыточности, последовательного раскрытия неопределенностей, консервативности и др.);
основные принципы распараллеливания работы вычислительных алгоритмов.

Основные задачи дисциплины:
грамотно формировать математические и вычислительные модели;
оптимально выбирать вычислительные методы решения;
использовать MatLAB для решения инженерных задач.

учебного плана, литература по курсу
Дисциплина “Компьютерное обеспечение инженерных задач” опирается в первую очередь на курс высшей математики и информатики. В целом дисциплина близка дисциплине “Математическое моделирование систем”, читаемой во многих высших учебных заведениях.

В качестве литературы по дисциплине можно рекомендовать:
Амисов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994. 546 с.
Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования. Построения и анализ моделей с примерами на языке MATLAB. СПб.: БГТУ. 1994. 192 с.
Потемкин В.Г. MATLAB справочное пособие. М.: Диалог МИФИ, 1997. 350 с.
С. Е. Душин, А. В. Красов, Н. Н. Кузьмин, Л. Б. Пошехонов. Численное моделирование систем управления: Учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2003. 78 с.

В нестоящее время есть очень много математических пакетов предназначенных для автоматизации инженерных расчетов. Их можно разделить на специальные (такие как Simulink, NOCSYD) и универсальные, представляющие из себя математические среды программирования. К числу универсальных математических пакетов необходимо отнести MATLAB, MathCAD, REDUCE, MACSYMA, DERIVE, MAPLE, Mathematica, Theorist.
В системах компьютерной алгебры REDUCE, MACSYMA, DERIVE, MAPLE, Mathematica, Theorist преобладает целочисленное представление и символьная обработка данных.
MathCAD ориентирован на естественную математическую форму записи.

Пакет MATLAB ориентирован на работу с реальными системами, в отличие перечисленных в начале пакетов на основе компьютерной алгебры все действия выполняются с плавающей арифметикой. Открытая архитектура пакета позволяет легко дополнять его своими приложениями. Для решения проблем на стыке символьных вычислений и вычислений с плавающей точкой в состав системы MATLAB включен пакет символьных вычислений.

Рис. 1.13. Пример выполнения расчетов в пакете MathCad

системы MATLAB значительно расширя­ется при использовании дополнительных пакетов программ, так называемых toolbox — ящик с инструментами.
Toolbox представляет собой проблемно-ориентирован набор функций, предоставляющий дополнительные возможности для решения задач, характерных для конкретной научной отрасли.
Основными toolbox являются:
“Системы управления” (Control System);
“Робастное управление” (Robust Control);
“Оптимизация” (Optimization);
“Идентификация систем” (System Identification) 49,50].
“Сплайны” (Spline);
“Обработка сигналов” (Signal Processing);
“Нейронные сети” (Neural Network).
Если в 60-80-х годах языком программирования математических задач являлся язык FORTRAN, с написанными под него громадным количеством математических библиотек, то в настоящее время им стал специализированная система программирования MATLAB с его системой toolbox.

знакомство с MATLAB

Подсказка “>>” показывает готовность системы к выполнению Ваших команд.
Набрав простейшие математические выражения в естественной форме записи Вы сразу же получаете результат.
<Выражение> или <Имя переменной>=<Выражение>.
В первом случае на самом деле результат выражения присваивается специальной служебной переменной имеющей имя ans, Вы так же можете использовать эту переменную в расчетах.
Если Вы не хотите что бы MATLAB выводил результаты промежуточных выражений на экран, то Вам необходимо поставить в конце выражения символ “;”.

При наборе и редактировании команд действуют такие же команды как в любом другом оконном редакторе Windows, например в блокноте. MATLAB предоставляет пользователю возможность пролистать предыдущие команды, сделать это можно с помощью клавиш стрелка вверх и вниз. Вы легко можете внести изменения в эти команды и повторно их выполнить.

Фактически MATLAB содержит один тип данных - массив или матрица (таблица). Массив это группа ячеек памяти имеющие одно имя.

Рис. 1.15. Типы данных в MatLab

Локальные и глобальные переменные

Для указания что переменная является глобальной необходимо указать перед ее именем описание global. Например global A.

Для того чтобы узнать какие переменные есть в Вашем распоряжении Вам необходимо вызвать команду who, по которой будет выдан список всех локальных переменных. Команда who global, выводит список всех глобальных переменных созданных Вами за время этого сеанса работы с MATLAB.

Рис.1.15. Глобальные переменные

Массивы

Присвоение значений матрице
А=[1 2 3 4 5]
B=[1 ; 3 ; 5 ; 7].
С=[ 1 2 3 ; 4 5 6 ; 7 8 9].

Создание матриц специального вида
Для генерации векторов пользователю предоставляется следующая команда:
<Имя вектора>=<Начальное значение>:<Шаг>:<Конечное значение>.
Например: Х=6 : 0. 2 : 26.

В математике часто встречаются матрицы специального вида. Ниже приведен ряд из них:
Единичная матрица
<Имя матрицы>=eye(<Размер>).
Матрица со всеми единицами
<Имя матрицы>=ones(<Кол-во строк>, <Кол-во столбцов>). Например: A=ones(6, 3).
Нулевая матрица
<Имя матрицы>=zeros(<Кол-во строк>, <Кол-во столбцов>). Например: A=zeros(6, 3).
Случайная матрица
<Имя матрицы>=rand(<Кол-во строк>, <Кол-во столбцов>). Например: A=rand(6, 3).

Рис.1.16. Матрицы специального вида

Для доступа к ячейкам матрицы Вам необходимо указать имя матрицы, номер строки и номер столбца. Нумерация строк и столбцов ведется с единицы. Номера пишутся в круглых скобках. Общий формат записи:
<Имя массива>(<Номер строки>, <Номер столбца>).
Например A(1,2).

Простейшие действия над матрицами
Умножение матрицы на скаляр. В математики для всех матриц определена операция умножения матрицы на скаляр (число). Все значения матрицы в этом случае умножаются на это число.

Сложение, вычитание скаляра из матрицы. Кроме операции умножения матрицы на скаляр для матрицы и скаляра определены операции сложение и вычитания. Действия так же выполняются с каждой ячейкой матрицы отдельно. Пример:

Сложение матриц (вычитание). Эта операция допустима только с матрицами одинакового размера. При выполнении операции действие выполняется с соответствующими друг другу ячейками. Пример:

При выполнении операции перемножения матриц выполняется последовательное умножение строки на вектор. При этом количество столбцов в первой матрице должно равняться количеству строк во второй матрице. Матрица результата будет иметь количество столько же строк сколько и в первой матрице, и количество столбцов равное количеству столбцов во второй матрице.

математического выражения
Организация всех переменных системы MATLAB как матрицы вызывает следующие ограничения применения их в выражениях. На пример:
t = 1 : 5
t = 1 2 3 4 5
y = cos(t)
y = 0.5403 -0.4161 -0.9900 -0.6536 0.2837
z = y / t
z = – 0.0811
Результат - получается одно число, а ожидали функцию z(t)=cos(t)/t.
Для организации поэлементного деления одного массива на другой, в MATLAB предусмотрена специальная операция - “./” - поэлементное деление.
Результат этого выражения будет другой:
z = y ./ t
z = 0.5403 -0.2081 -0.3300 -0.1634 0.0567

Вывод одного графика
MATLAB предоставляет следующие функции для работы с графикой:
plot(<Массив>) - построение графика значений из массива Х от номера отсчета.
plot(<Массив точек по оси Х>,<Массив точек по оси Y>) - построение графика значений из массива Y от значений из массива Х.
При вызове команды создается окно с указанным графиком.


Вывод нескольких графиков
Для вывода нескольких графиков на одном окне Вам необходимо указать их последовательно, например:
t = –10 : 0.1 : 10 ;
x1 = sin(t) ;
x2 = cos(t) ./ t ;
plot(t,x1,t,x2)

графики функций y=sin(t)/t и (x/5)2+y2=1. Как не трудно заметить данные функции имеют три точки пересечения.

Графический метод решения уравнений
Вывод на экран сразу нескольких графиков предоставляет простейший способ найти приблизительное значение решения.

методом можно лишь примерно оценить решение. Для более точного нахождения решения в пакете MatLAB необходимо воспользоваться функцией fsolve(уравнение, начальное значение). Позже мы познакомимся как с помощью данной функции решать системы уравнений. В простейшем случае решаемое уравнение можно указать можно указать в одинарных кавычках, например: 'x*x-abs(x)'. Но данная функция имеет три решения, представленных на рис.1.17.

Функция fsolve продолжает итерационную процедуру до тех пор пока она не найдет решение с заданной точностью. По этому в нашем примере мы и получили 7.9062e-008 а не 0.
В случае более сложных функций их удобнее представить в виде M файла. Тогда в качестве первого параметра функции fsolve подставляется в одинарных кавычках имя этого файла.

Решение, которое найдет в этом случае функция fsolve будет определяться начальным значением откуда она начнет итерационную процедуру поиска решения. Например:
fsolve('x*x-abs(x)',-2), ans = -1.0000;
fsolve('x*x-abs(x)',0.6), ans = 1.0000;
fsolve('x*x-abs(x)',0.4), ans = 7.9062e-008.

MATLAB
Программирование в системе MatLAB очень близко к обычному программированию. Программа создается в любом текстовом редакторе. Файл должен иметь расширение *.M. Для того чтобы Вы могли вызвать его из любого места он должен размещаться в одном из каталогов перечисленных в конфигурационном файле MATLABRC.M. К строкам matlabpath =[...’путь’,...,’путь’] ; необходимо по аналогии добавить путь до своего рабочего каталога.
Для вызова M файла необходимо набрать его имя в командной строке MatLAB, и если необходимо его аргументы.
Важным элементом облегчающим программирование являются комментарии. Строка комментария начинается в MatLAB символом ‘%’.

Оператор проверки условия позволяет организовать разветвление исполнения программы. Внешний вид оператора представлен на рис.1.18.

Рис. 1.18. Блок-схема условного оператора: редуцированная и полная формы

Формат записи оператора, редуцированная форма:
if условие
операторы
end
полная форма:
if условие
операторы
else
операторы
end
Обращаю Ваше внимание что в отличие от современных языков программирования не используются такое понятие как составной оператор. Блок условного оператора обязательно заканчивается служебным словом end.
Пример:
d=b^2-4*a*c ;
if d<0
‘ корней нет’
else
x1=( –b + sqrt(d)) / (2*a)
x2=( –b – sqrt(d)) / (2*a)
end
Использованная в данном фрагменте текстовая строка, заключенная в одиночные кавычки выводится на экран:
ans =
корней нет

повторений

Формат оператора:
for переменная = начальное значение : [шаг :] конечное значение
операторы
end
Поле шаг в конструкции оператора не является обязательным. Например:
for i=1 : 100
x(i) = sin(2*PI*i /100) ;
end
Допустимо задание переменной цикла в виде вектора:
for i= [1 2 4 8 16 32]
x(i) = sin(2*PI*i /100) ;
end

for допустимо использование оператора прерывания цикла break.

Рис. 1.20. Иллюстрация использования оператора break

управления работой цикла может использоваться команда continue.

Рис. 1.21. Иллюстрация работы команды continue

повторений

Рис. 1.22. Блок-схема цикла while

Формат оператора цикла с неизвестным количеством повторений:
while условие
операторы
end
Тело цикла обязательно заканчивается служебным словом end.
Например, программа определения точности вычислений:
a=1 ;
while a+1 != 1
a=a/2 ;
end
a
Последняя строчка программы выведет на экран значение переменной а.

Шаблон описания функции в MatLAB выглядит следующим образом:
function результат = имя ( аргументы )
операторы
Первая строчка является обязательной, указывающий что это функциональный M файл. После нее располагаются операторы - тело функции.
Имя функции обязательно должно совпадать с именем файла в котором она размещается. Пример:
function y=minf(x, n)
y=x(1) ;
for i=1:n
if x(i) y=x(i) ;
end
end
Если из функции необходимо вернуть несколько значений (или массивов), то они перечисляются в прямоугольных скобках.
function [y, k]=minf(x, n)
y=x(1) ;
k=1;
for i=1:n
if x(i) y=x(i) ;
k=i ;
end
end

Лабораторная работа №1 имеет два этапа и коллоквиум по предшествующей лекции. Коллоквиум имеет собственную систему регистрации и выполняется индивидуально каждым из студентов отдельно.
Структура лабораторной работы приведена на рис. 1.23.

Рис. 1.23. Структура лабораторной работы №1

первом этапе Вам предлагается найти точки пересечения графиков функций.
x = –2 : 0.5 : 4 ; % создаем вектор точек по оси X
y1 = a1*x.^3 + b1*x.^2+c1*x+d1 ; % точки первого графика
y2 = a2*x.^3 + b2*x.^2+c2*x+d2 ; % точки второго графика
plot( x, y1, x, y2) % строим графики двух функций

Рис. 1.24. Поиск решений графическим методом

После этого используя функцию fsolve() осуществляем поиск решений с заданной точностью:
A(1) = fsolve(‘a1*x^3+b1*x^2+c1*x+d­–(a2*x^3+b2*x^2+c2*x+d2)’, x01)
…
A(k) = fsolve(‘a1*x^3+b1*x^2+c1*x+d­–(a2*x^3+b2*x^2+c2*x+d2)’, x0k)
Обратите внимание, что в этом случае x не является вектором.

нелинейными устройствами
Во время выполнения второго этапа Вам необходимо преобразовать сигнал нелинейным элементом, заданным интервальной функцией.

Рис. 1.25. Схема выполнения второго этапа

представленного на рис. 1.26 Вам необходимо составить систему уравнений вида:

Создаем алгоритм функции, реализующий данное преобразование (рис. 1.27).

Рис. 1.26. Заданный вид нелинейного элемента

функции описывающей нелинейный элемент

function y = prim( x )
if x < x1
y = y1 ;
else
if x < x2
y = y1 + (y2–y1) / (x2–x1)*(x–x1) ;
else
y = y2 ;
end
end

Если функция сохранена в Вашем рабочем каталоге группы, то необходимо проложить путь до этого каталога:
path( matlabpath, ‘e:\stud\mi411’).
Рекомендуется проверить правильность работы функции, для этого предлагается вызвать функцию в узловых точках нелинейной характеристики, например:
prim( 6.3 ).

После этого, формируем точки входного сигнала и в цикле последовательно пропускаем их через созданную функцию нелинейного элемента:
dt = ( tend – t0 ) / (N – 1) ; % рассчитываем значение шага между точками
t = t0 : dt : tend ; % формируем вектор значений
u = a1*sin(w1*t + f1)+a2*sin(w2*t + f2) +e ; % рассчитываем входной сигнал
for i = 1 : N
y = prim( u(i) ) ; % преобразуем отсчеты входного сигнала нелинейным элементом
end
plot(t, u, t, y) % строим график входного и выходного сигналов

Кроме того, рекомендуется построить график вольт/амперной характеристики нелинейного элемента по массивам входного и выходного сигналов:
plot( u, y ).

этапа лабораторной работы приведена на рис. 1.28.

Рис. 1.28. Иллюстрация II этапа лабораторной работы