ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ презентация

Содержание

1. ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ
2. 1. Теорема Бернулли: условия применимости Теорема Бернулли
3. 2. Теорема Бернулли: измене-ние кинетической энергии
4. 3. Теорема Бернулли: работа внешних сил
5. 4. Теорема Бернулли: результат
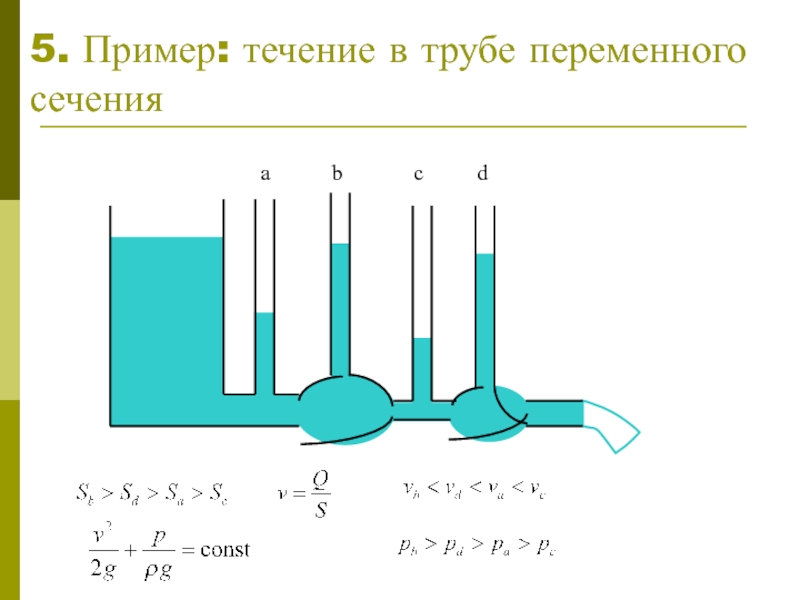
6. 5. Пример: течение в трубе переменного сечения
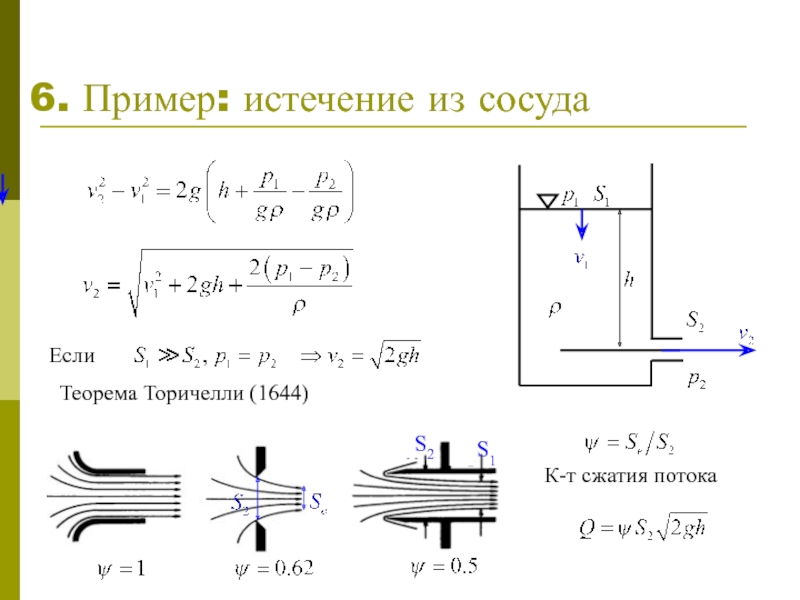
7. 6. Пример: истечение из сосуда Если
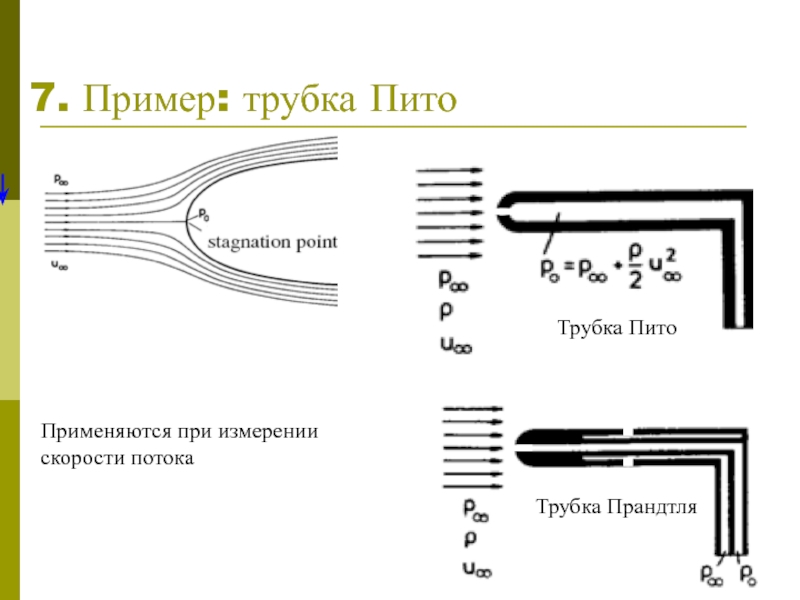
8. 7. Пример: трубка Пито
9. 8. Пример: трубка Вентури
10. 9. Теорема о вириале - среднее за
11. 10. Пример: замкнутая гравитационная система Теорема о
12. 11. Пример: упругая цепочка - потенциальная энергия системы
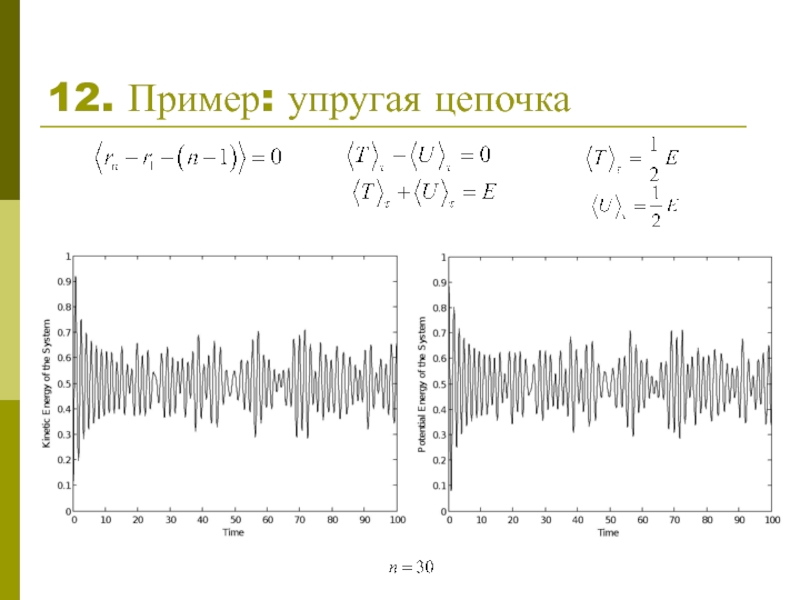
13. 12. Пример: упругая цепочка

1. Теорема Бернулли: условия применимости Теорема Бернулли – результат применения теоремы об изменении кинетической энергии к установившемуся движению жидкости. Это – основная теорема гидродинамики, имеющая многочисленные приложения при изучении течения воды

Главная
Разное
ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ

Слайд 1ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ
ЛЕКЦИЯ 4:
ТЕОРЕМА БЕРНУЛЛИ, ТЕОРЕМА О ВИРИАЛЕ

Слайд 21. Теорема Бернулли: условия применимости
Теорема Бернулли – результат применения теоремы об

изменении кинетической энергии к установившемуся движению жидкости. Это – основная теорема гидродинамики, имеющая многочисленные приложения при изучении течения воды в реках, каналах, трубах, при исследовании действия воды в водяных двигателях и т. д.

Теорема Бернулли имеет дело с идеальной жидкостью:
1) Несжимаемой
2) Невязкой

ВАЖНО: Работа внутренних сил в идеальной жидкости равна нулю!

Теорема Бернулли имеет дело с установившемся течением:
в каждой точке пространства, наполненного жидкостью, явления не изменяются с течением времени; направление и величина скорости в этой точке, величина давления у этой точки остаются постоянными во все время движения.

Слайд 32. Теорема Бернулли: измене-ние кинетической энергии

Изменение кинетической энергии за время dt
Q

–объемный расход жидкости [м3/c]
– плотность жидкости [кг/м3]

Слайд 43. Теорема Бернулли: работа внешних сил

1) Работа сил тяжести
2) Работа сил

давления

3) Работа сил со стороны стенок трубы равна нулю

Предполагается, что трения жидкости о стенки нет, значит силы нормальны к стенке. Скорости частиц жидкости касательны к стенке. Скалярное произведение есть ноль.

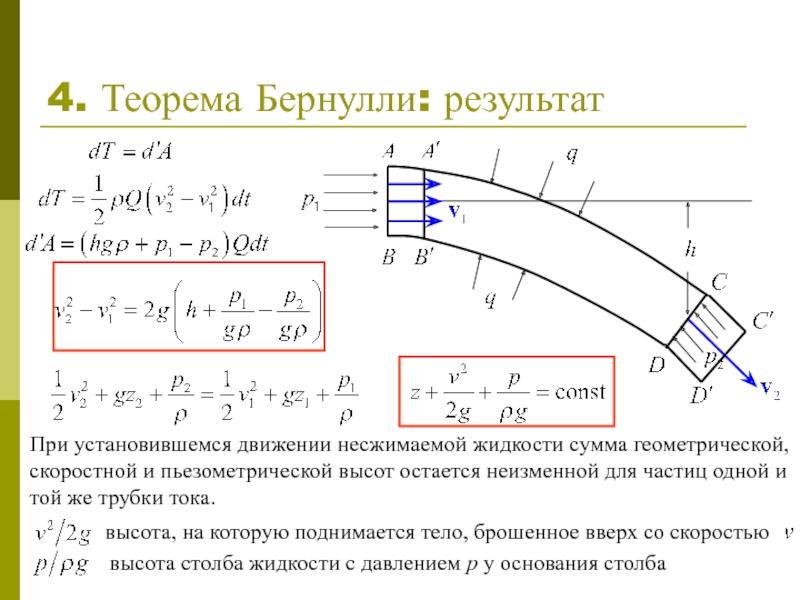
Слайд 54. Теорема Бернулли: результат

При установившемся движении несжимаемой жидкости сумма геометрической, скоростной

и пьезометрической высот остается неизменной для частиц одной и той же трубки тока.

высота, на которую поднимается тело, брошенное вверх со скоростью

высота столба жидкости с давлением p у основания столба

Слайд 65. Пример: течение в трубе переменного сечения

a
b
c
d

Слайд 76. Пример: истечение из сосуда

Если
Теорема Торичелли (1644)

S1
S2
К-т сжатия потока

Слайд 87. Пример: трубка Пито

Трубка Пито
Трубка Прандтля
Применяются при измерении скорости потока

Слайд 98. Пример: трубка Вентури

Применяются при измерении расхода жидкости в трубе
S1
S1
S2
S2

Слайд 109. Теорема о вириале
- среднее за время
Левая часть обращается в

ноль если выполнено одно из условий
Интервал не ограничен, а функция ограничена
Движение периодическое с периодом

вириал системы

При выполнении условий 1 или 2 среднее за время значение кинетической энергии равно ее вириалу

Слайд 1110. Пример: замкнутая гравитационная система
Теорема о вириале
Сохранение энергии

Указывает в какой пропорции

начальная энергия «делится в среднем» между кинетической и потенциальной энергией во время движения замкнутой гравитационной системы

Задача : пусть

тогда

Слайд 1211. Пример: упругая цепочка

- потенциальная энергия системы

Слайд 1312. Пример: упругая цепочка

Скачать презентацию

ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ презентация

Содержание

Слайд 1ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ
ЛЕКЦИЯ 4:
ТЕОРЕМА БЕРНУЛЛИ, ТЕОРЕМА О ВИРИАЛЕ

Слайд 21. Теорема Бернулли: условия применимости
Теорема Бернулли – результат применения теоремы об

Слайд 32. Теорема Бернулли: измене-ние кинетической энергии

Изменение кинетической энергии за время dt
Q

Слайд 43. Теорема Бернулли: работа внешних сил

1) Работа сил тяжести
2) Работа сил

Слайд 54. Теорема Бернулли: результат

При установившемся движении несжимаемой жидкости сумма геометрической, скоростной

Слайд 65. Пример: течение в трубе переменного сечения

a
b
c
d

Слайд 76. Пример: истечение из сосуда

Если
Теорема Торичелли (1644)

S1
S2
К-т сжатия потока

Слайд 87. Пример: трубка Пито

Трубка Пито
Трубка Прандтля
Применяются при измерении скорости потока

Слайд 98. Пример: трубка Вентури

Применяются при измерении расхода жидкости в трубе
S1
S1
S2
S2

Слайд 109. Теорема о вириале
- среднее за время
Левая часть обращается в

Слайд 1110. Пример: замкнутая гравитационная система
Теорема о вириале
Сохранение энергии

Указывает в какой пропорции

Слайд 1211. Пример: упругая цепочка

- потенциальная энергия системы

Слайд 1312. Пример: упругая цепочка

Обратная связь

Что такое ThePresentation.ru?

ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ презентация

Содержание

Слайд 1ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫЛЕКЦИЯ 4: ТЕОРЕМА БЕРНУЛЛИ, ТЕОРЕМА О ВИРИАЛЕ

Слайд 21. Теорема Бернулли: условия применимостиТеорема Бернулли – результат применения теоремы об

Слайд 32. Теорема Бернулли: измене-ние кинетической энергииИзменение кинетической энергии за время dtQ

Слайд 43. Теорема Бернулли: работа внешних сил1) Работа сил тяжести2) Работа сил

Слайд 54. Теорема Бернулли: результатПри установившемся движении несжимаемой жидкости сумма геометрической, скоростной

Слайд 65. Пример: течение в трубе переменного сеченияabcd

Слайд 76. Пример: истечение из сосудаЕслиТеорема Торичелли (1644)S1S2К-т сжатия потока

Слайд 87. Пример: трубка ПитоТрубка ПитоТрубка ПрандтляПрименяются при измерении скорости потока

Слайд 98. Пример: трубка ВентуриПрименяются при измерении расхода жидкости в трубеS1S1S2S2

Слайд 109. Теорема о вириале- среднее за время Левая часть обращается в

Слайд 1110. Пример: замкнутая гравитационная системаТеорема о вириалеСохранение энергииУказывает в какой пропорции

Слайд 1211. Пример: упругая цепочка- потенциальная энергия системы

Слайд 1312. Пример: упругая цепочка

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ
ЛЕКЦИЯ 4:
ТЕОРЕМА БЕРНУЛЛИ, ТЕОРЕМА О ВИРИАЛЕ

Слайд 21. Теорема Бернулли: условия применимости
Теорема Бернулли – результат применения теоремы об

Слайд 32. Теорема Бернулли: измене-ние кинетической энергии

Изменение кинетической энергии за время dt
Q

Слайд 43. Теорема Бернулли: работа внешних сил

1) Работа сил тяжести
2) Работа сил

Слайд 54. Теорема Бернулли: результат

При установившемся движении несжимаемой жидкости сумма геометрической, скоростной

Слайд 65. Пример: течение в трубе переменного сечения

a
b
c
d

Слайд 76. Пример: истечение из сосуда

Если
Теорема Торичелли (1644)

S1
S2
К-т сжатия потока

Слайд 87. Пример: трубка Пито

Трубка Пито
Трубка Прандтля
Применяются при измерении скорости потока

Слайд 98. Пример: трубка Вентури

Применяются при измерении расхода жидкости в трубе
S1
S1
S2
S2

Слайд 109. Теорема о вириале
- среднее за время
Левая часть обращается в

Слайд 1110. Пример: замкнутая гравитационная система
Теорема о вириале
Сохранение энергии

Указывает в какой пропорции

Слайд 1211. Пример: упругая цепочка

- потенциальная энергия системы