(БАЛАНСИРОВКА БЕЗ ФАЗОВЫХ ИЗМЕРЕНИЙ)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ДИНАМИЧЕСКАЯ БАЛАНСИРОВКА РОТОРОВ В СОБСТВЕННЫХ ПОДШИПНИКАХ С ИСПОЛЬЗОВАНИЕМ ТЕХНИЧЕСКИХ СРЕДСТВ ОБЕСПЕЧИВАЮЩИХ ИЗМЕРЕНИЕ ТОЛЬКО АМПЛИТУД ВЕКТОРОВ ВИБРАЦИИ презентация
Содержание
- 1. ДИНАМИЧЕСКАЯ БАЛАНСИРОВКА РОТОРОВ В СОБСТВЕННЫХ ПОДШИПНИКАХ С ИСПОЛЬЗОВАНИЕМ ТЕХНИЧЕСКИХ СРЕДСТВ ОБЕСПЕЧИВАЮЩИХ ИЗМЕРЕНИЕ ТОЛЬКО АМПЛИТУД ВЕКТОРОВ ВИБРАЦИИ
- 2. В течение ряда лет в учебном центре
- 3. Подводные камни «безфазной балансировки» Большее, чем
- 4. ОСНОВНЫЕ ТРЕБОВАНИЯ КОТОРЫЕ НЕОБХОДИМО ОБЕСПЕЧИТЬ ПРИ ПРОВЕДЕНИИ
- 5. Перед проведением работ необходимо убедиться в том,
- 6. Если результаты измерения уровней вибрации виброметром по
- 7. Допущение о линейности колебательной системы на
- 8. Допущение о линейности колебательной системы на воздействие
- 9. «Метод обхода пробным грузом» Плоскость, в
- 10. Уравновешивающий груз определяется по формуле: Mу=Mп*So/(So-Smin)
- 11. «Метод последовательных приближений» Плоскость, в которой необходимо
- 12. Способ предложенный А.Г. Верете: Радиусом R1, равным
- 13. Метод трех пусков (вариант 1) Измеряем
- 14. Вектор "В1" меньше "А", а "В2" больше
- 15. Мы имеем вектор исходной вибрации "А" и
- 16. При безфазной балансировке всегда есть два правильных
- 17. При первом запуске определяем амплитуду вибрации с
- 18. Получаем систему треугольников, в каждом из которых
- 19. Метод трех пусков с использованием ПО
- 20. ООО «Балтех» Россия, Санкт-Петербург, 194044,
Слайд 1ДИНАМИЧЕСКАЯ БАЛАНСИРОВКА РОТОРОВ В СОБСТВЕННЫХ ПОДШИПНИКАХ С ИСПОЛЬЗОВАНИЕМ ТЕХНИЧЕСКИХ СРЕДСТВ ОБЕСПЕЧИВАЮЩИХ
Слайд 2В течение ряда лет в учебном центре ООО «Балтех» при чтении
Слайд 3Подводные камни «безфазной балансировки»
Большее, чем при традиционной балансировке, количество пусков
Зачастую при использовании некоторых методов безфазной балансировки, существует два правильных решения. Выбирая единственно правильное, Вам придется полагаться на интуицию и здравый смысл.
Наличие двух правильных решений объясняется просто – задача описывается системой линейных уравнений, которая сводится к квадратному уравнению и, соответственно, имеет два математически правильных решения
Слайд 4ОСНОВНЫЕ ТРЕБОВАНИЯ КОТОРЫЕ НЕОБХОДИМО ОБЕСПЕЧИТЬ ПРИ ПРОВЕДЕНИИ БАЛАНСИРОВКИ БЕЗ ФАЗОВЫХ ИЗМЕРЕНИЙ:
ЧАСТОТНЫЙ
УРОВЕНЬ ВИБРАЦИИ НА ЧАСТОТЕ ВРАЩЕНИЯ ДОЛЖЕН ПРЕОБЛАДАТЬ В РАБОЧЕЙ ПОЛОСЕ ЧАСТОТ ВИБРОМЕТРА
КОЛЕБАТЕЛЬНАЯ СИСТЕМА (АГРЕГАТ) ДОЛЖНА БЫТЬ ЛИНЕЙНА ОТНОСИТЕЛЬНО ВОЗДЕЙСТВИЯ НА НЕЕ ПРОБНЫХ (КОРРЕКТИРУЮЩИХ) МАСС, УСТАНАВЛИВАЕМЫХ В ПЛОСКОСТЯХ БАЛАНСИРОВКИ
В ПРОЦЕССЕ БАЛАНСИРОВКИ ДОЛЖНО БЫТЬ ВЫПОЛНЕНО НЕ МЕНЕЕ ДВУХ ПУСКОВ С ПРОБНОЙ МАССОЙ
ПРИ ПУСКАХ С ПРОБНЫМИ МАССАМИ УРОВНИ ВИБРАЦИИ ДОЛЖНЫ БЫТЬ ИЛИ БОЛЬШЕ ИЛИ МЕНЬШЕ ЧЕМ В ИСХОДНОМ СОСТОЯНИИ
ВОЗМОЖНА СИТУАЦИЯ, КОГДА ЗАДАЧА ИМЕЕТ ДВА ПРАВИЛЬНЫХ РЕШЕНИЯ
БАЛАНСИРОВКА ВЫПОЛНЯЕТСЯ ДЛЯ ОДНОЙ БАЛАНСИРОВОЧНОЙ ПЛОСКОСТИ С ОДНОЙ ТОЧКОЙ КОНТРОЛЯ
Слайд 5Перед проведением работ необходимо убедиться в том, что на агрегате действительно
Проверить это достаточно просто, если виброметр измеряет хотя бы два вибропараметра из:
СКЗ виброускорения
СКЗ виброскорости
Пик-Пик виброперемещения
Слайд 6Если результаты измерения уровней вибрации виброметром по любым двум вибропараметрам соответствуют
На частоте вращения взаимосвязь между этими вибропараметрами описывается выражениями:
v = 159.15 * a / f где: a – виброускорение, СКЗ, в м/с2
s = 450.14 * v / f v – виброскорость, СКЗ, в мм/с
s – виброперемещение, Пик-Пик, в мкм
f – частота вращения ротора, в Гц
Слайд 7
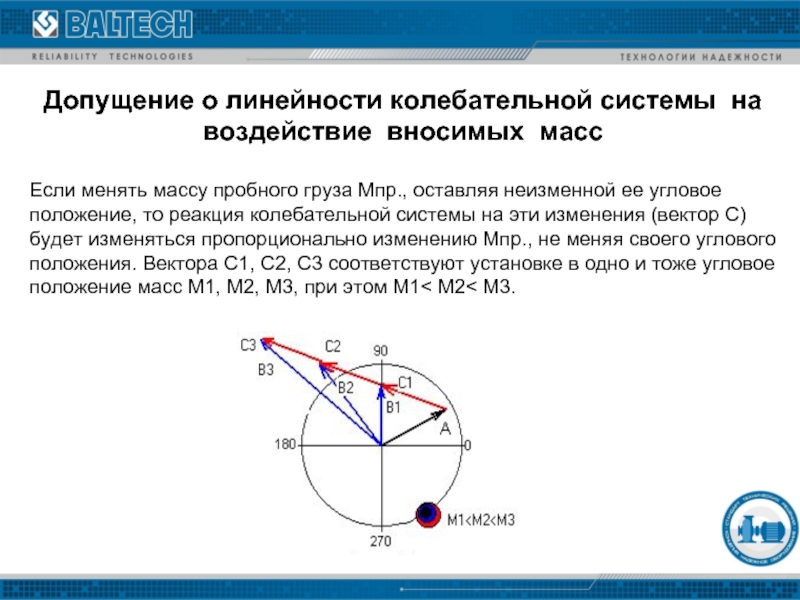
Допущение о линейности колебательной системы на воздействие вносимых масс
Если менять массу
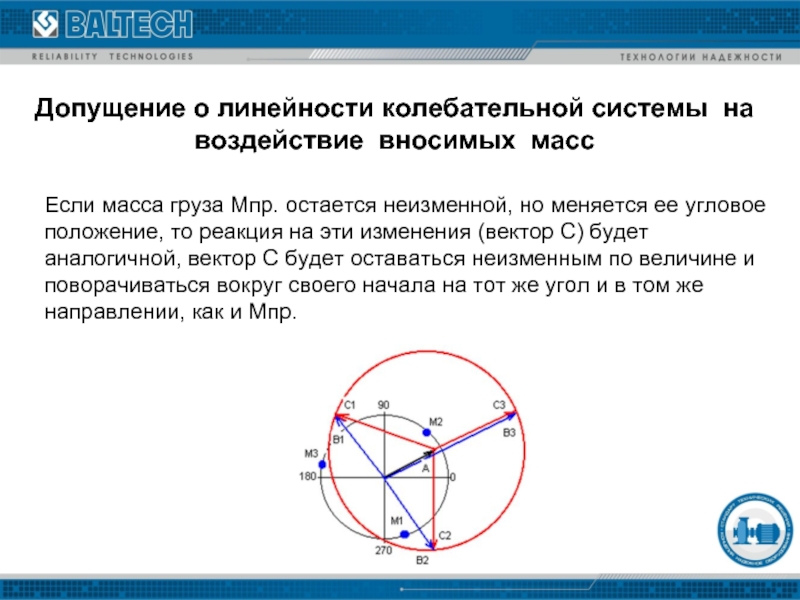
Слайд 8Допущение о линейности колебательной системы на воздействие вносимых масс
Если масса груза
Слайд 9«Метод обхода пробным грузом»
Плоскость, в которой необходимо произвести балансировку, делят на
В каждой точке на определенном радиусе R устанавливают пробный груз Mп. Машину доводят до рабочей скорости вращения и измеряют амплитуду вибрации (допустим, виброперемещение).
Слайд 10Уравновешивающий груз определяется по формуле:
Mу=Mп*So/(So-Smin)
So - виброперемещение без пробного груза.
Уравновешивающий груз
Далее строят график (в удобном масштабе) где S – ось виброперемещения.
Если при построении получилась кривая похожая на синусоиду - пробный груз выбран правильно и отсутствуют дефекты препятствующие проведению балансировки.
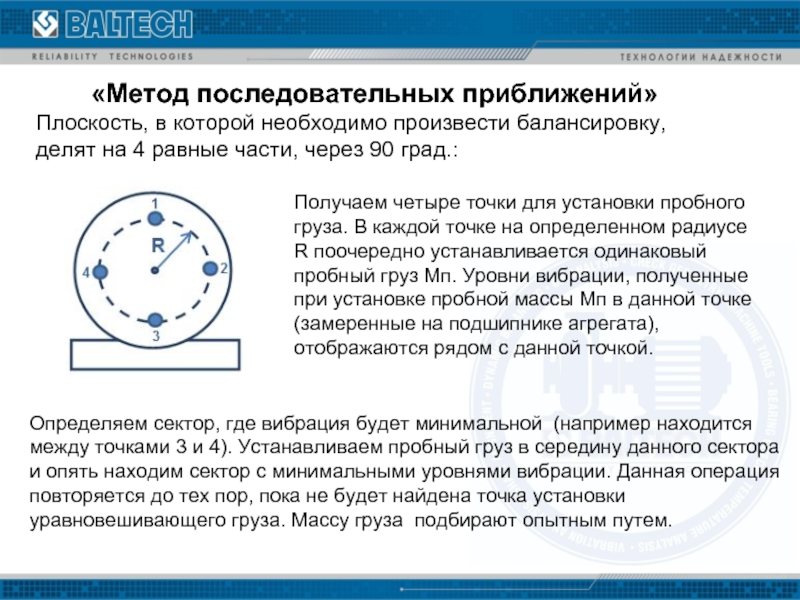
Слайд 11«Метод последовательных приближений»
Плоскость, в которой необходимо произвести балансировку, делят на 4
Получаем четыре точки для установки пробного груза. В каждой точке на определенном радиусе R поочередно устанавливается одинаковый пробный груз Mп. Уровни вибрации, полученные при установке пробной массы Mп в данной точке (замеренные на подшипнике агрегата), отображаются рядом с данной точкой.
Определяем сектор, где вибрация будет минимальной (например находится между точками 3 и 4). Устанавливаем пробный груз в середину данного сектора и опять находим сектор с минимальными уровнями вибрации. Данная операция повторяется до тех пор, пока не будет найдена точка установки уравновешивающего груза. Массу груза подбирают опытным путем.
Слайд 12Способ предложенный А.Г. Верете:
Радиусом R1, равным (пропорциональным) виброперемещению без пробного груза,
Из точек А и В окружности, расположенных под прямым углом, радиусом R2 и R3 пропорциональными виброперемещению, при установке поочередно пробного груза, делаем дуги. Проводим прямую через центр окружности О и точку пересечения дуг С до пересечения с окружностью.
Точка D - место установки
уравновешивающего груза.
Определяем массу
уравновешивающего груза
по формуле:
Му=Мп*R1/ОС.
«методы амплитуд»
Слайд 13Метод трех пусков (вариант 1)
Измеряем уровень вибрации в исходном состоянии "А"
Устанавливаем в произвольном месте
балансировочной плоскости пробный груз "М1" и измеряем получившийся уровень вибрации "В1". Пусть он получился меньше уровня "А". На графике его можно изобразить в виде окружности радиуса "В1" с центром в начале вектора "А".
Переместим груз "М1" (тот же самый) на 90 градусов и измерим получившийся уровень вибрации "В2". Пусть он получился больше уровня "А". Поскольку фаз мы не знаем изображаем его также в виде окружности радиуса "В2" с центром в начале вектора "А".
Слайд 14Вектор "В1" меньше "А", а "В2" больше "А". Это обязательное условие,
Если этого не произошло, значит неудачно было выбрано
первоначальное место установки пробного груза и процедуры нужно повторить с другим местом установки груза.
Слайд 15Мы имеем вектор исходной вибрации "А" и две окружности, на которых
векторы "С1" и "С2" должны быть расположены под углом
90 градусов друг к другу и направление от вектора "С1" к вектору "С2" должно быть такое же, как направление перемещения пробного груза, т.е. в данном случае - против часовой стрелки.
Из допущений о линейности нам известно, что:
оба вектора "С1" и "С2" должны начинаться в одной и той же точке - конце вектора "А".
векторы "С1" и "С2" должны быть равны по величине, поскольку пробные груза были одинаковы.
В результате мы получаем два правильных решения. По одному решению: груз необходимо сместить в одну сторону и увеличить, по другому - на такой же угол в другую сторону и уменьшить.
Мур. = Мпр.* А/С;
Угол (Мур.) = Угол (Мпр.) + Угол (между векторами А и С)
Слайд 16При безфазной балансировке всегда есть два правильных решения, действительно математически правильных.
Как в предыдущем случае, по одному решению, груз необходимо сместить в одну сторону и увеличить, по другому - на такой же угол в другую сторону и уменьшить.
Мур. = Мпр.* А/С;
Угол (Мур.) = Угол (Мпр.) + Угол (между векторами А и С)
Каким решением воспользоваться? Это уже можно решить на уровне здравого смысла. Лучше сначала поставить тот груз, который меньше, просто из соображений безопасности.
Слайд 17При первом запуске определяем амплитуду вибрации с начальным (исходным) дисбалансом ротора
Метод трех пусков (вариант 2)
Слайд 18Получаем систему треугольников, в каждом из которых неизвестна одна сторона Ап,
На основании теоремы косинусов:
А12=А02+Ап2 – 2А0Апcosγ;
A22=А02+Ап2 – 2А0Апcos(γ – α);
A32=А02+Ап2 – 2А0Апcos(β - γ).
Угловое положение γ корректирующей массы относительно положения первой пробной массы (в том же направлении, что α и β ) и величину корректирующей массы mк определяем по:
где α - угол между первым и вторым положением пробной массы;
β - угол между первым и третьим положением пробной массы;