- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Декартова система координат на плоскости презентация
Содержание
- 1. Декартова система координат на плоскости
- 2. Зададим на плоскости две оси координат,
- 3. Плоскость, на которой задана декартова система координат,
- 4. у х О
- 5. Прямоугольная система координат хОу разделяет
- 6. Если на плоскости задана прямоугольная система координат
- 7. Если на плоскости задана прямоугольная система координат
- 8. (х1; у1) у х О х1
- 9. Если на плоскости задана прямоугольная система координат
- 10. Ответьте на вопросы: где находятся точки, абсциссы
- 11. Проверьте себя: 1) где находятся точки,
- 12. Ренэ Декарт (1598 – 1650) Французский философ
- 13. Об авторе Новую
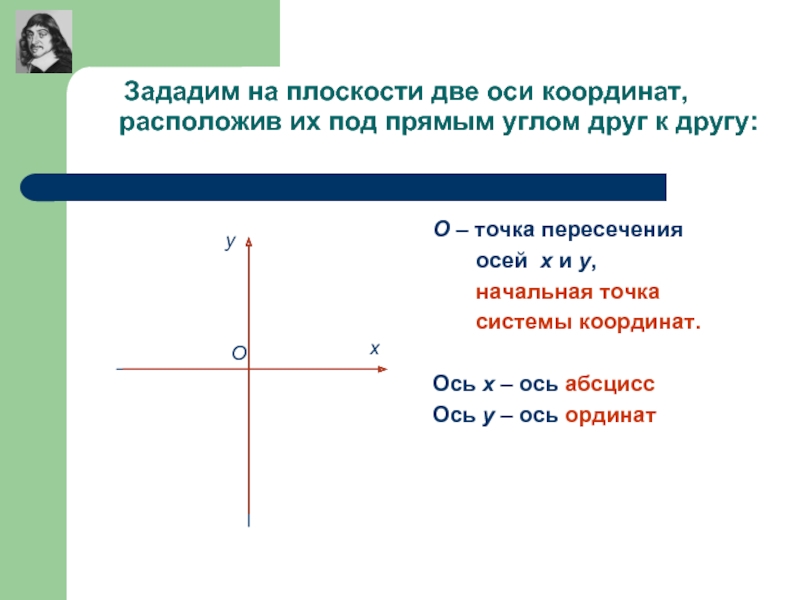
Слайд 2 Зададим на плоскости две оси координат, расположив их под прямым
О – точка пересечения
осей х и у,
начальная точка
системы координат.
Ось х – ось абсцисс
Ось у – ось ординат
х
у
О
Слайд 3Плоскость, на которой задана декартова система координат, называется координатной плоскостью
точка плоскости.
Проведем через точку А
прямые, параллельные
осям координат.
Прямая, параллельная
оси у, пересечет ось х в
точке А1.
Прямая, параллельная
оси х, пересечет ось у в
точке А2.
А1 – абсцисса точки А
А2 – ордината точки А
у
х
О
1
1
-1
-1
2
3
4
2
3
4
-2
-3
-4
-2
-3
-4
.
А
А1
А2
А (4; 3)
А (х; у)
Слайд 4
у
х
О
1
1
-1
-1
2
3
4
2
3
4
-2
-3
-4
-2
-3
-4
.
.
.
.
.
А
В
С
D
Е
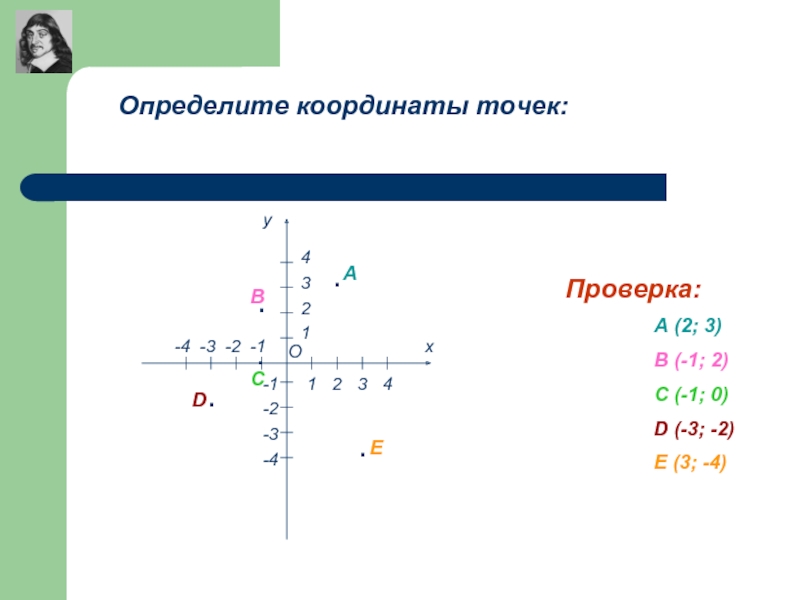
Определите координаты точек:
Проверка:
В (-1; 2)
С (-1; 0)
D (-3; -2)
Е (3; -4)
Слайд 5Прямоугольная система координат хОу разделяет плоскость на четыре угла,
I x>0, y>0
II x<0, y>0
III x<0, y<0
IV x>0, y<0
х
у
О
I
II
III
IV
Слайд 6Если на плоскости задана прямоугольная система координат хОу, то:
каждой точке плоскости
.
х1
у1
х
у
О
А
А (х1; у1)
Слайд 7Если на плоскости задана прямоугольная система координат хОу, то:
разным точкам плоскости
х
у
О
.
.
А (х1; у1)
В (х2; у2)
Слайд 8 (х1; у1)
у
х
О
х1
у1
А
Если на плоскости задана прямоугольная
система координат хОу, то:
чисел соответствует
некоторой одной
точке плоскости
.
Слайд 9Если на плоскости задана прямоугольная система координат хОу, то:
каждой точке плоскости
разным точкам плоскости поставлены в соответствие разные упорядоченные пары чисел;
каждая упорядоченная пара чисел соответствует некоторой одной точке плоскости
Иначе говоря, между точками плоскости и упорядоченными парами чисел имеет место взаимно однозначное соответствие
Слайд 10Ответьте на вопросы:
где находятся точки, абсциссы которых равны нулю?
где находятся
в каких координатных углах находятся точки, абсциссы которых положительны?
в каких координатных углах находятся точки, ординаты которых положительны?
Слайд 11Проверьте себя:
1) где находятся точки, абсциссы которых равны нулю?
2) где
3) в каких координатных углах находятся точки, абсциссы которых положительны?
4) в каких координатных углах находятся точки, ординаты которых положительны?
1) на оси у; 2) на оси х; 3) I, IV; 4) I, II
Слайд 12Ренэ Декарт (1598 – 1650)
Французский философ и математик.
В области точных наук
введение более простых обозначений в алгебру;
основная теорема в теории определения числа положительных и отрицательных корней уравнения;
методы проведения касательных к кривым;
изобретение аналитической геометрии и многочисленных ее приложений.
В физике:
установление закона инерции;
сложение движений;
закон преломления и отражения света и др.
Назад