- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ДЕКАРТОВА СИСТЕМА КООРДИНАТ презентация
Содержание
- 1. ДЕКАРТОВА СИСТЕМА КООРДИНАТ
- 2. Рене Декарт (1596-1650 гг.) Декарт (Descartes) Рене ‑ французский
- 3. Декартова система координат
- 4. Однажды
- 5. Проследим путь открытия системы координат согласно этой
- 6. На рисунке условно показаны три стены кабинета:
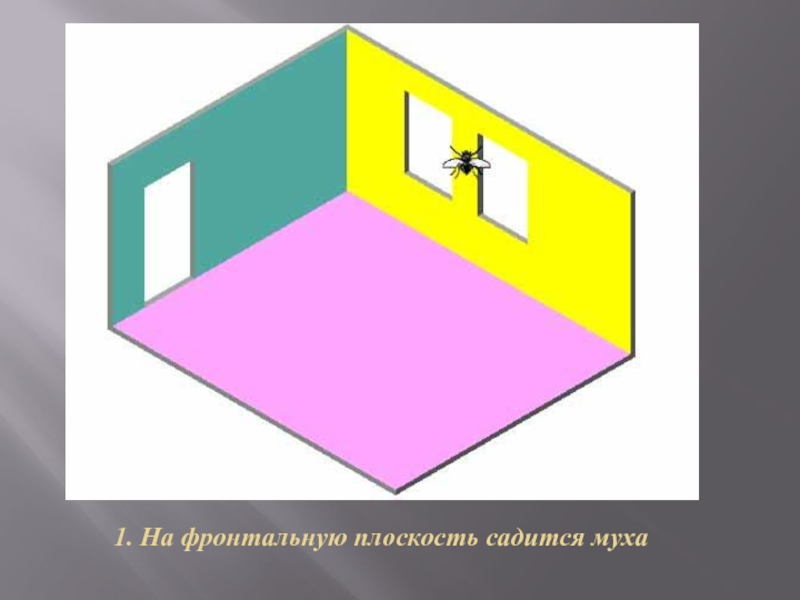
- 7. 1. На фронтальную плоскость садится муха
- 8. 2. Предположим, что Р. Декарт смотрит на фронтальную плоскость в перпендикулярном ей направлении.
- 9. Мы видим, что муха находится на фронтальной плоскости. Но как точно определить ее положение?
- 10. 3)
- 11. 4. Определим точное положение "соавтора" ‑ мухи. Проведем через
- 12. Принято координаты объекта, обычно точки, записывать в
- 13. Новизна идеи состоит в том, что положение
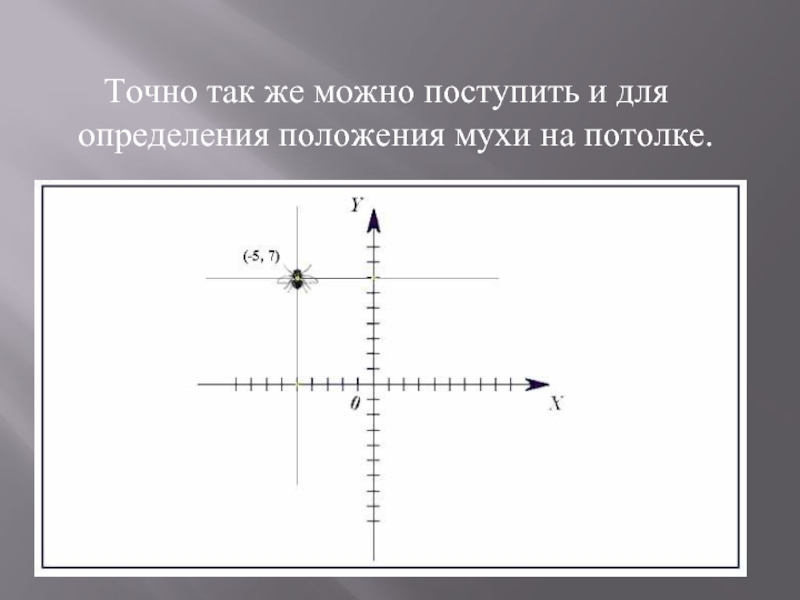
- 14. Точно так
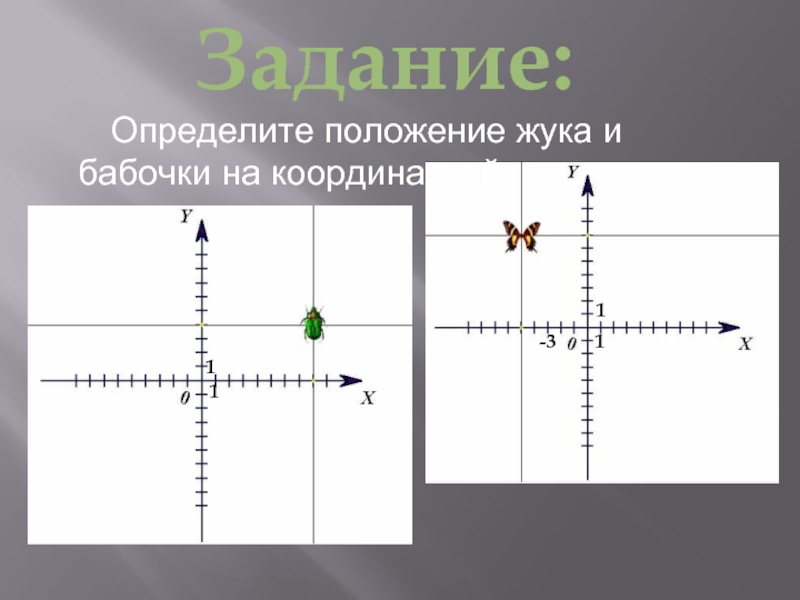
- 15. Определите положение жука
- 16. Все эти примеры демонстрируют преимущества координатного способа
Слайд 2Рене Декарт (1596-1650 гг.)
Декарт (Descartes) Рене ‑ французский философ, математик, физик и физиолог.
Рене Декарт является одним из создателей аналитической геометрии (которую он разрабатывал одновременно с П. Ферма), позволявшей алгебраизировать эту науку с помощью метода координат, т.е. вместо геометрических построений использовать математические расчеты. Предложенная им система координат получила его имя.
Слайд 4
Однажды Рене Декарт весь день пролежал
в кровати, думая о чем-то, а муха жужжала вокруг и не давала ему сосредоточиться. Он стал размышлять, как бы описать положение мухи в любой момент времени математически, чтобы иметь возможность прихлопнуть ее без промаха.
И ... придумал декартовы координаты, одно из величайших изобретений в истории человечества.
И ... придумал декартовы координаты, одно из величайших изобретений в истории человечества.
ЛЕГЕНДА ОБ ИЗОБРЕТЕНИИ
СИСТЕМЫ КООРДИНАТ
Слайд 5Проследим путь открытия системы координат согласно этой легенде.
Время открытия: 1637 год.
Действующие
лица:
1)Автор открытия: французский математик Рене Декарт.
2)"Соавтор" открытия: муха Декарта
Место действия: "кабинет" Рене Декарта.
1)Автор открытия: французский математик Рене Декарт.
2)"Соавтор" открытия: муха Декарта
Место действия: "кабинет" Рене Декарта.
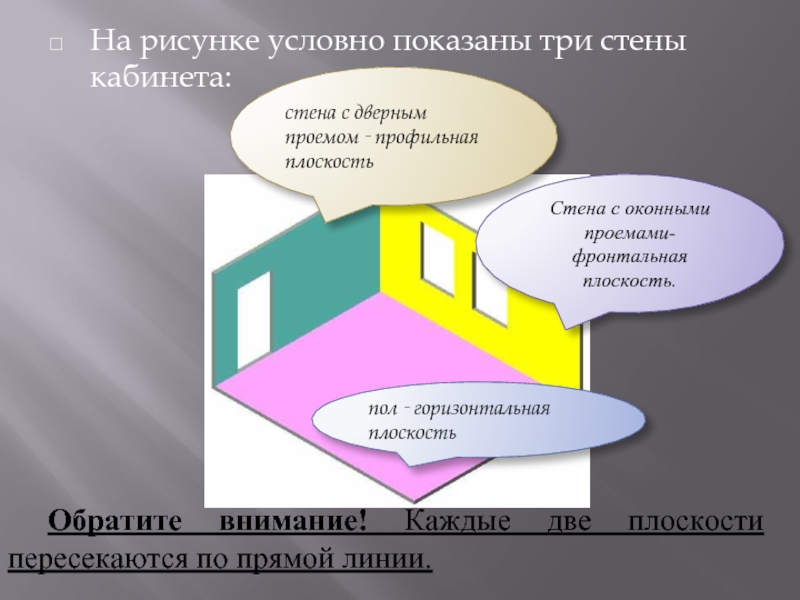
Слайд 6На рисунке условно показаны три стены кабинета:
Обратите внимание! Каждые две плоскости
пересекаются по прямой линии.
стена с дверным проемом ‑ профильная плоскость
Стена с оконными проемами- фронтальная плоскость.
пол ‑ горизонтальная плоскость
Слайд 82. Предположим, что Р. Декарт смотрит на фронтальную плоскость в перпендикулярном ей
направлении.
Слайд 10 3) Эврика! НУЖНО взять две взаимно перпендикулярные числовые прямые. Точку пересечения
прямых обозначим как О ‑ начало системы координат.
Одну из прямых назовем ось X, другую ‑ ось Y.
На нашем рисунке расстояние между делениями на числовых прямых равно единице.
Слайд 114. Определим точное положение "соавтора" ‑ мухи.
Проведем через точку, где находится муха две
прямые:
А) Параллельно оси X. Прямая пересекает ось Y в точке с числовым значением, равным 4. Это значение назовем координатой "у" нашего "соавтора".
Б) Параллельно оси Y. Прямая пересекает ось Х в точке с числовым значением, равным (-2). Это значение назовем координатой "х" нашего объекта.
А) Параллельно оси X. Прямая пересекает ось Y в точке с числовым значением, равным 4. Это значение назовем координатой "у" нашего "соавтора".
Б) Параллельно оси Y. Прямая пересекает ось Х в точке с числовым значением, равным (-2). Это значение назовем координатой "х" нашего объекта.
Слайд 12Принято координаты объекта, обычно точки, записывать в форме (x; y). Для нашей
мухи мы можем сказать, что она находится в точке с координатами (-2; 4).
Задача точного определения положения мухи решена!
Слайд 13Новизна идеи состоит в том, что положение точки или объекта на
плоскости определяетcя с помощью двух пересекающихся осей.
Слайд 16Все эти примеры демонстрируют преимущества координатного способа определения положения мухи, жука
и бабочки на плоскости с помощью системы координат Декарта.