- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Чему равно скалярное произведение двух векторов? презентация
Содержание
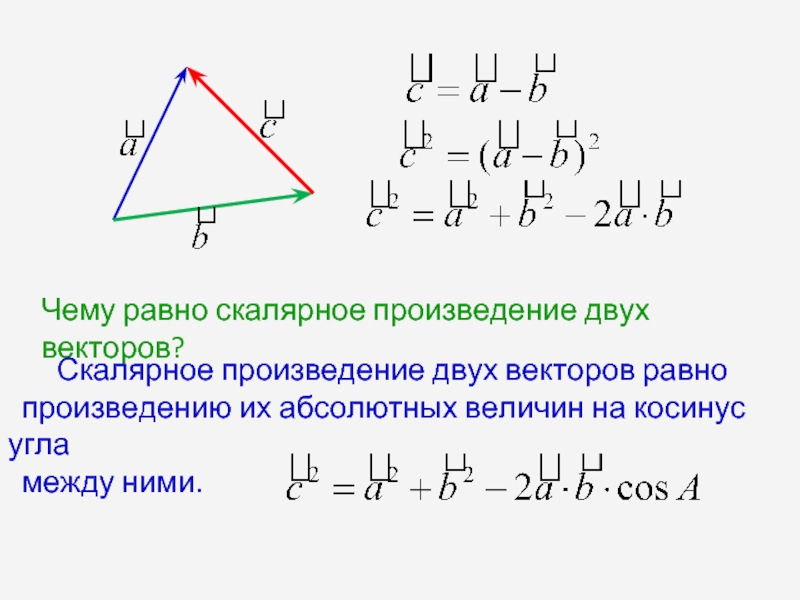
Слайд 1Чему равно скалярное произведение двух векторов?
Скалярное произведение
произведению их абсолютных величин на косинус угла
между ними.
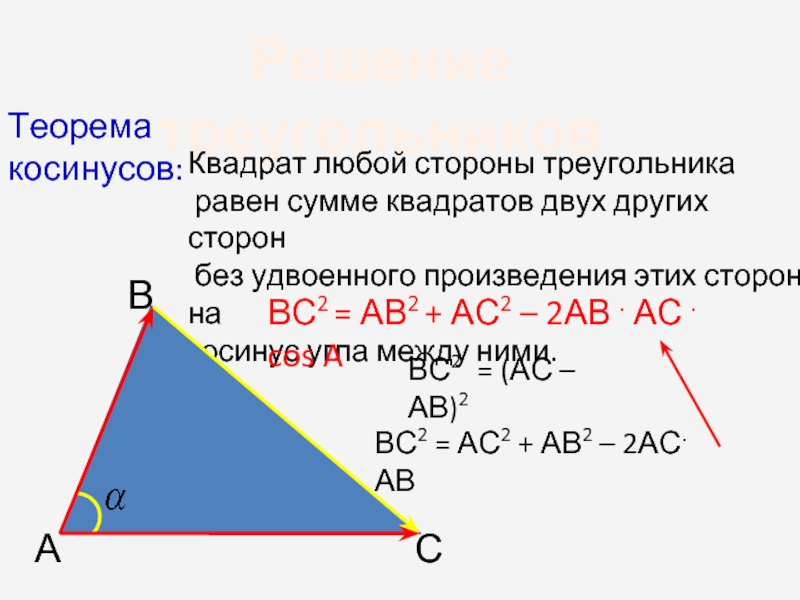
Слайд 2Решение треугольников
Теорема косинусов:
Квадрат любой стороны треугольника
равен сумме квадратов двух других
без удвоенного произведения этих сторон на
косинус угла между ними.
А
В
С
ВС2 = АВ2 + АС2 – 2АВ . АС . cos A
ВС2 = (АС –АВ)2
ВС2 = АС2 + АВ2 – 2АС. АВ
Слайд 3
А
В
С
А
В
С
D
D
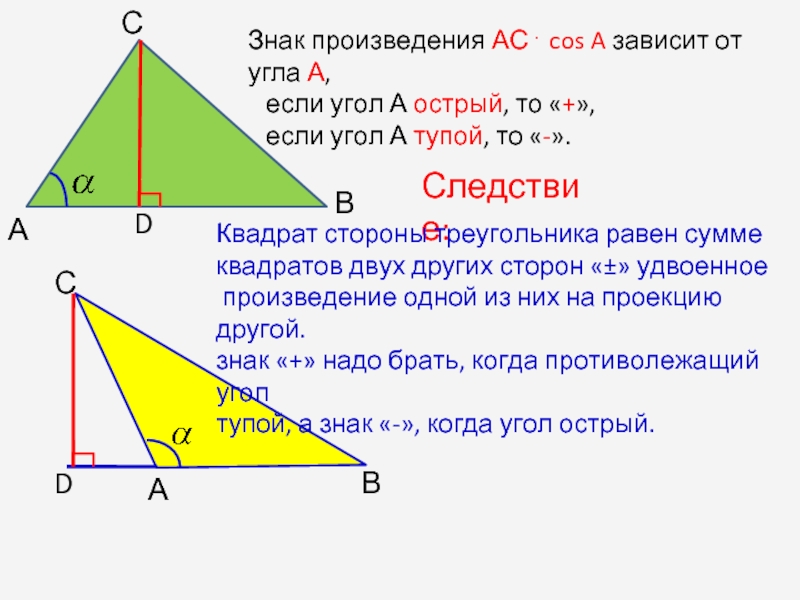
Знак произведения АС . cos A зависит от угла А,
если угол А тупой, то «-».
Следствие:
Квадрат стороны треугольника равен сумме
квадратов двух других сторон «±» удвоенное
произведение одной из них на проекцию другой.
знак «+» надо брать, когда противолежащий угол
тупой, а знак «-», когда угол острый.