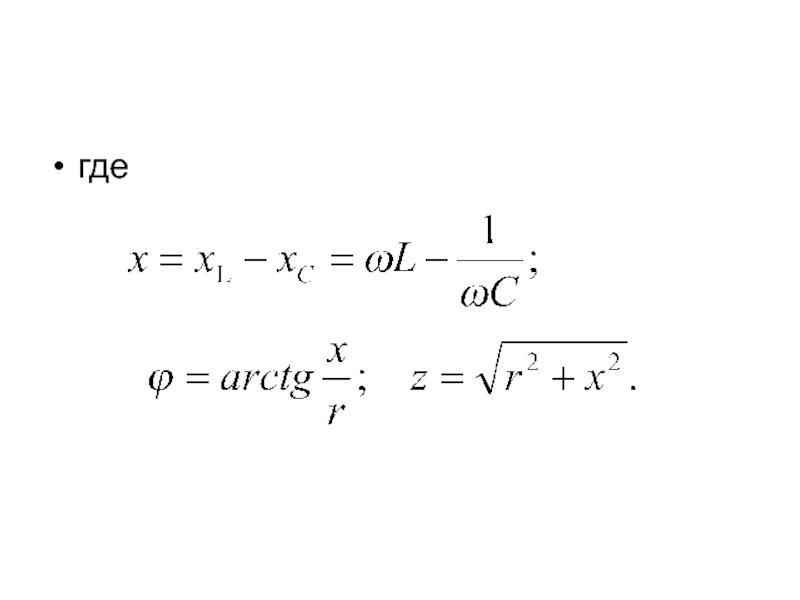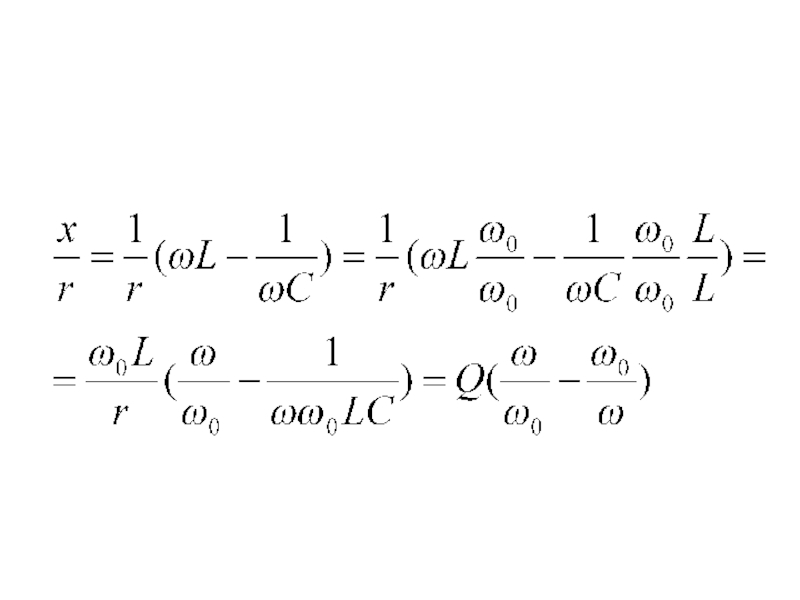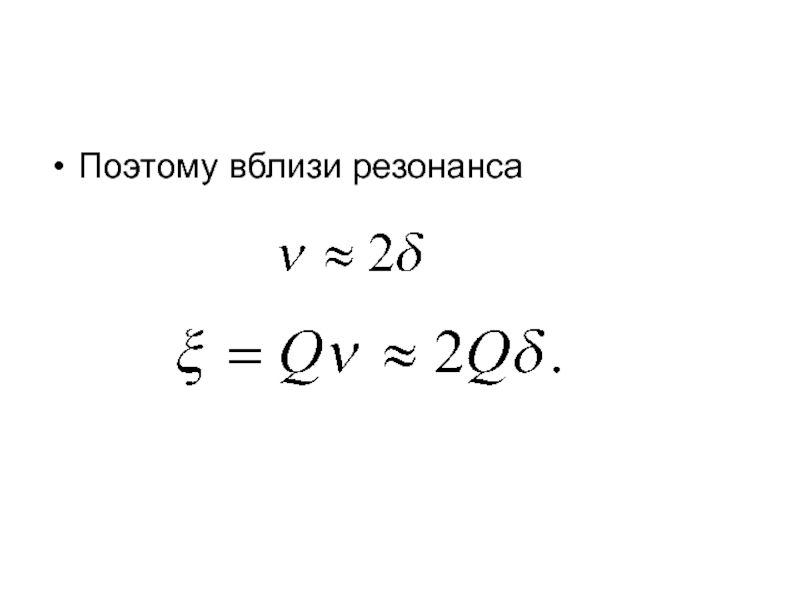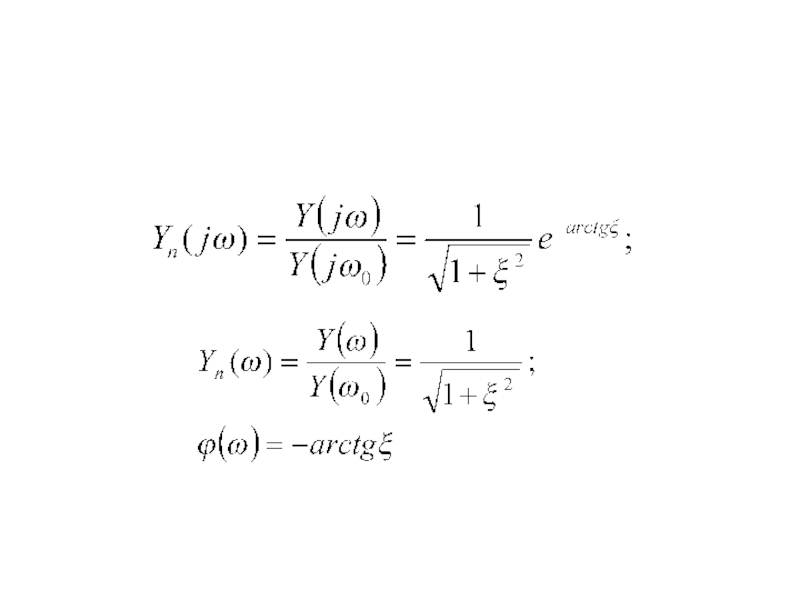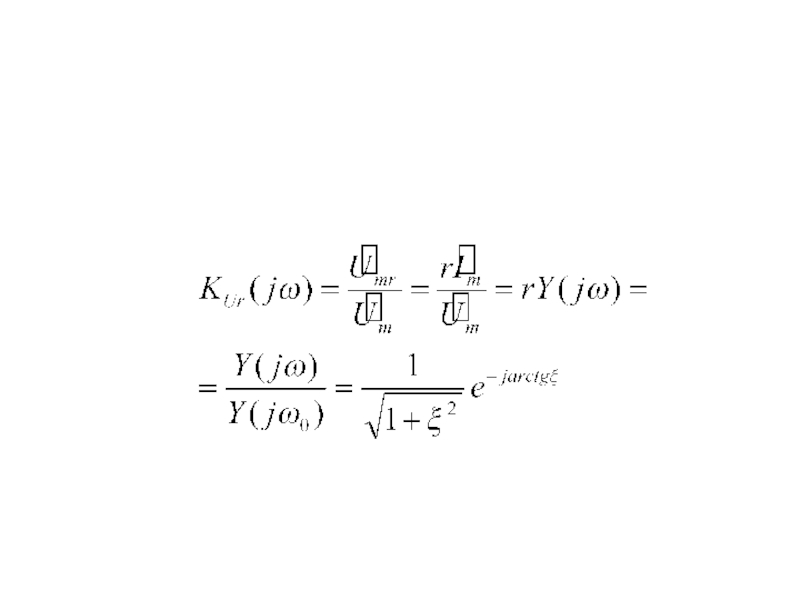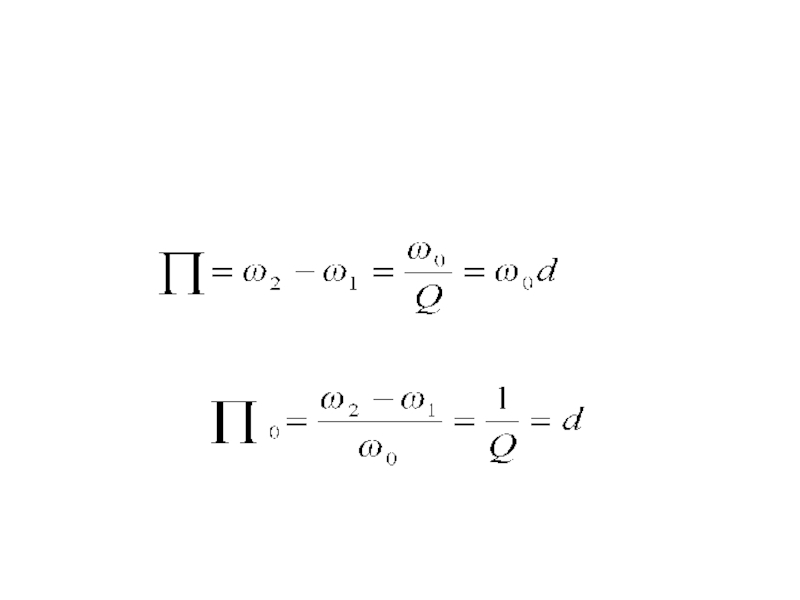та кіберпросторах
Тема 4. Частотні характеристики лінійних електричних кіл другого порядку.
Заняття 1. Частотні властивості послідовного коливального контуру.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Частотні характеристики лінійних електричних кіл другого порядку. Частотні властивості послідовного коливального контуру презентация
Содержание
- 1. Частотні характеристики лінійних електричних кіл другого порядку. Частотні властивості послідовного коливального контуру
- 2. Л I Т Е Р А Т
- 3. 1. Условия и признаки резонанса напряжений.
- 4. Элементы электроники
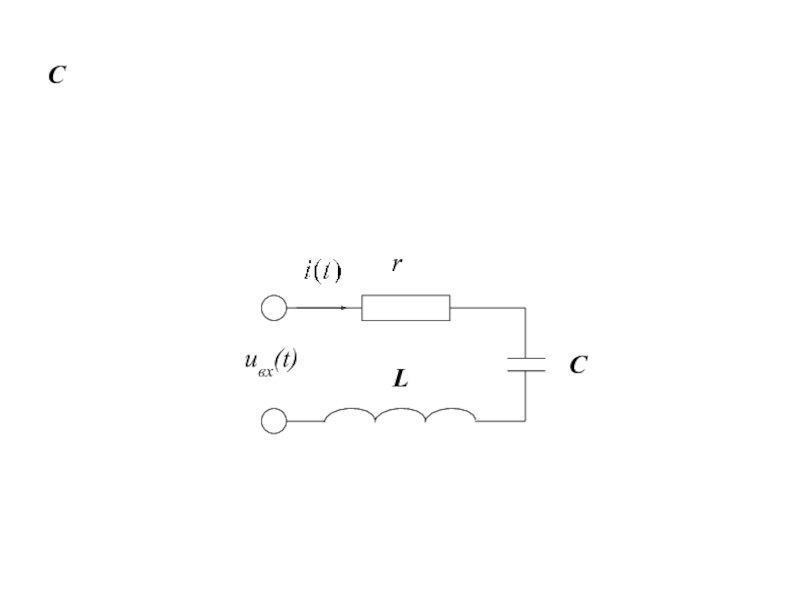
- 5. C
- 6. Пусть напряжение на зажимах контура изменяется по закону
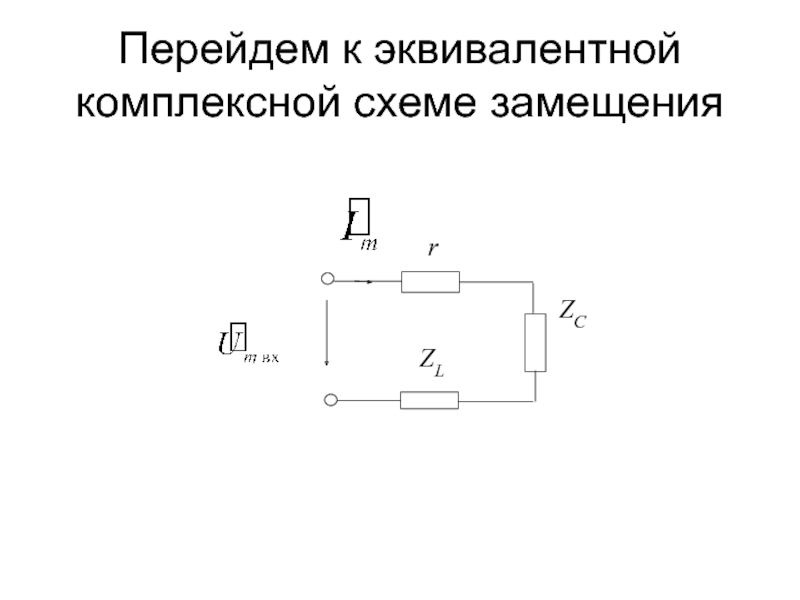
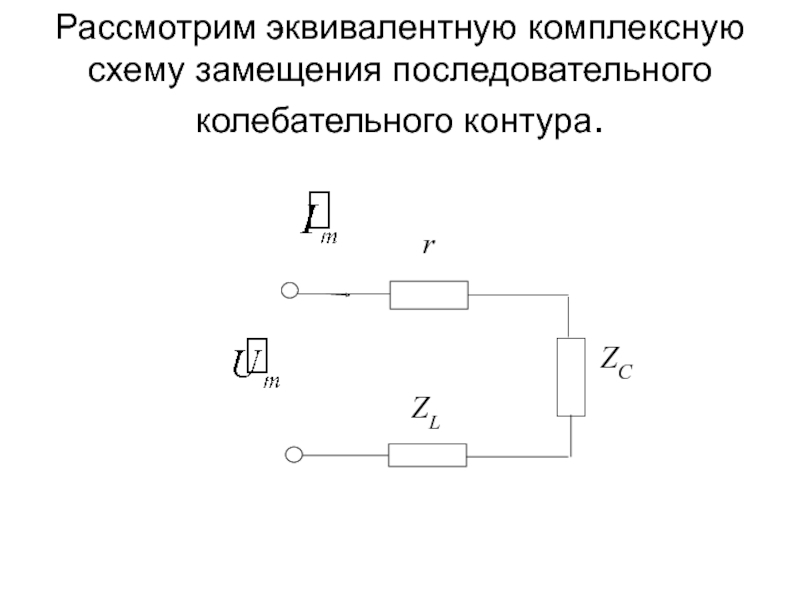
- 7. Перейдем к эквивалентной комплексной схеме замещения
- 8. По второму закону Кирхгофа составим уравнение электрического равновесия:
- 9. Комплексное сопротивление цепи Zвх=
- 10. где
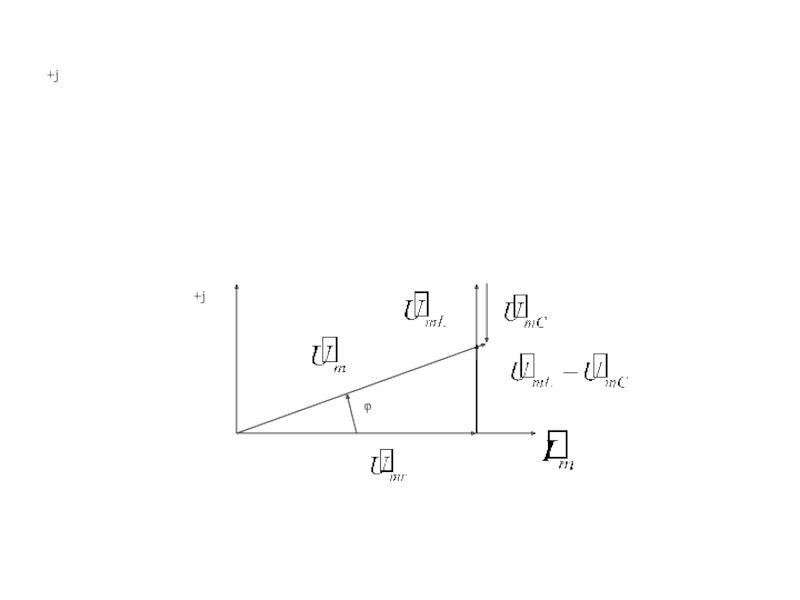
- 12. +j
- 13. При xL
- 14. +j
- 15. Наибольший интерес представляет случай равенства xL=
- 16. +j
- 17. Уменьшение комплексного сопротивления контура до минимального
- 18. Другое определение: резонансом называется резкое возрастание
- 19. При xL= xC сдвиг фаз между
- 20. Первый признак резонанса в последовательном колебательном
- 21. Второй признак резонанса напряжений в последовательном
- 22. Учитывая то, что при резонансе xL =
- 23. 2. Первичные и вторичные параметры последовательного колебательного
- 24. Рассмотрим, какие параметры относятся к вторичным
- 25. Это резонансная частота контура или
- 26. Волновое или характеристическое сопротивление контура. Модули реактивных
- 27. Величина называется волновым или характеристическим сопротивлением контура.
- 28. Добротность контура Резонансные свойства контура характеризуются
- 29. отношение волнового сопротивления контура к активному сопротивлению.
- 30. Добротность определяет эффективность или качество контура,
- 31. Это наименование параметра связано с тем,
- 32. 3. Комплексні функції та частотні характеристики ПКК
- 33. Комплексная входная проводимость: Комплексной входной функцией цепи
- 34. 3.1 Комплексная входная проводимость последовательного
- 37. Нормированная комплексная входная проводимость получается путем
- 38. Нормированная входная АЧХ описывается выражением
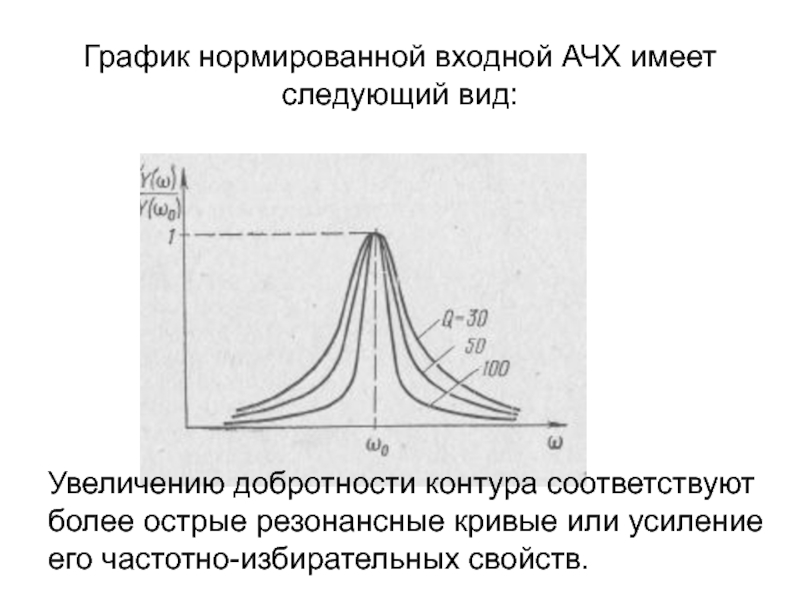
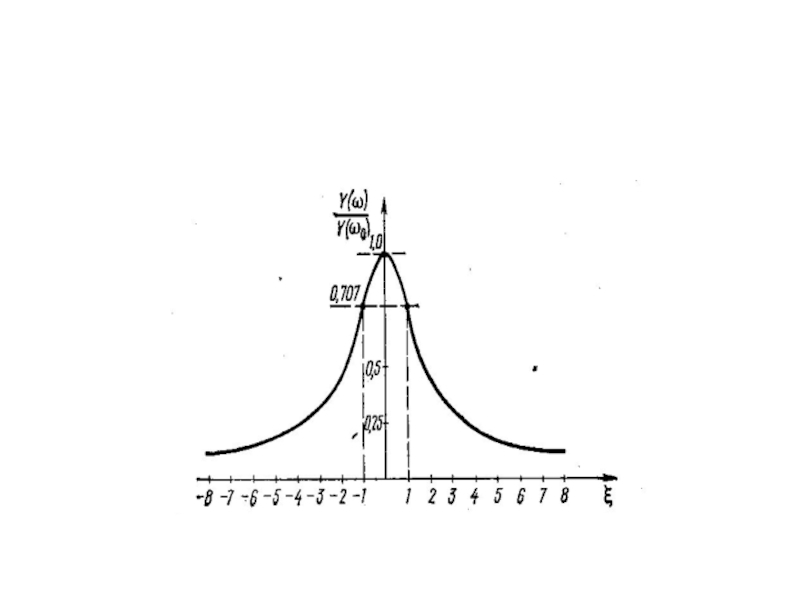
- 39. График нормированной входной АЧХ имеет следующий вид:
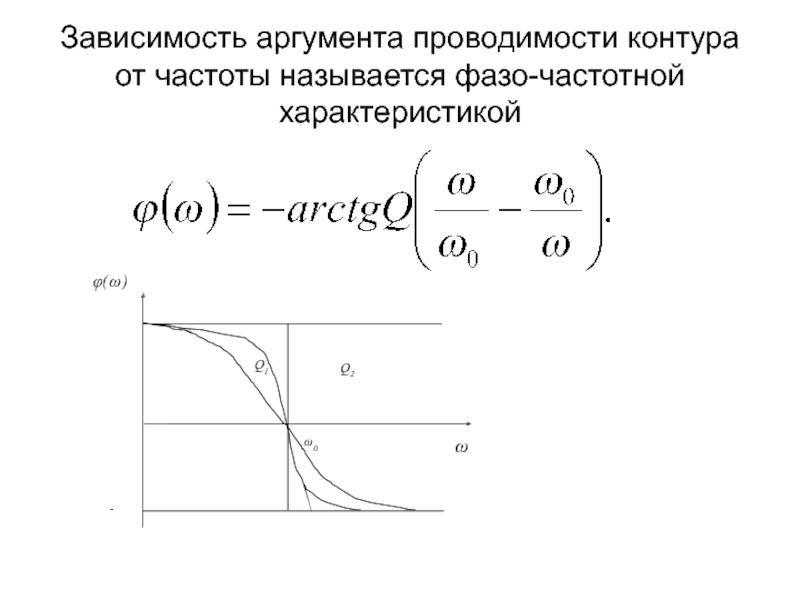
- 40. Зависимость аргумента проводимости контура от частоты называется фазо-частотной характеристикой
- 41. Из этого графика следует, что на
- 42. При исследовании частотных характеристик колебательного контура
- 43. Разность между частотой сигнала и резонансной
- 44. Отношение абсолютной расстройки к резонансной частоте называется относительной расстройкой.
- 45. Фактором расстройки называют величину, описываемую выражением
- 46. Обобщенной расстройкой называют преобразованное отношение реактивного сопротивления контура к активному
- 47. так как При малых расстройках в
- 48. Поэтому вблизи резонанса
- 49. Относительная и обобщенная расстройки, как и
- 54. Для передаточной функции по напряжению на
- 56. Этому соответствует амплитудно-частотная и фазо-частотная характеристики:
- 57. Передаточная функция по напряжению на емкости
- 58. Ей соответствуют частотные характеристики:
- 59. Для передаточной функции по напряжению на индуктивности
- 60. Частотные характеристики в этом случае:
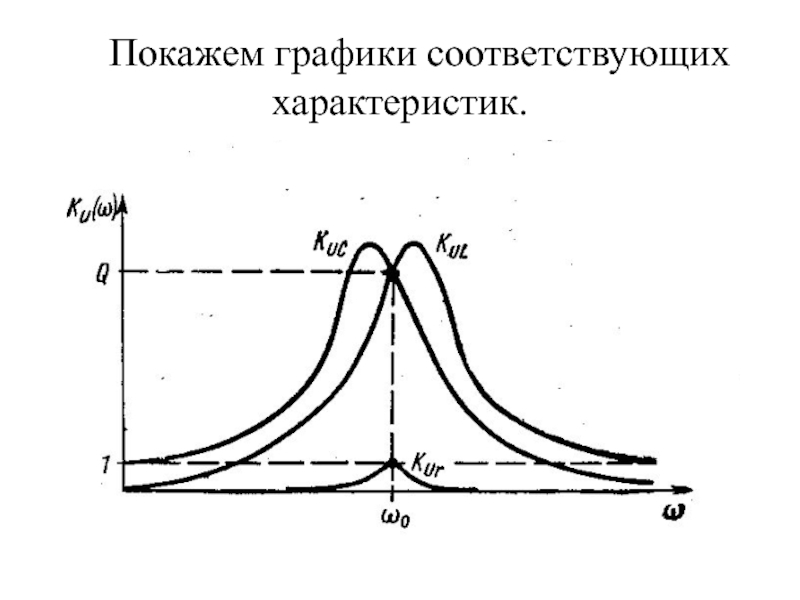
- 61. Покажем графики соответствующих характеристик.
- 62. Численно передаточные функции, или коэффициенты передачи по
- 63. 4. Резонансні характеристики ПКК Резонансными характеристиками ПКК
- 64. Рассмотрим эквивалентную комплексную схему замещения последовательного колебательного контура.
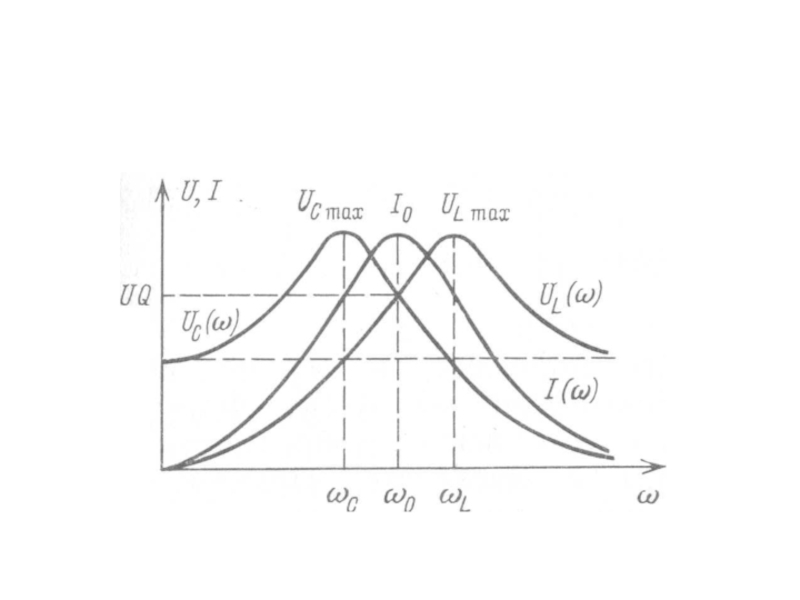
- 65. Зависимость амплитуды тока от частоты имеет следующий вид:
- 66. Проанализируем это уравнение, для чего воспользуемся случаями предельных значений частоты:
- 67. Амплитуды напряжений на реактивных элементах можно найти согласно закону Ома:
- 69. При
- 70. При частоте, равной резонансной, наблюдается равенство
- 71. При
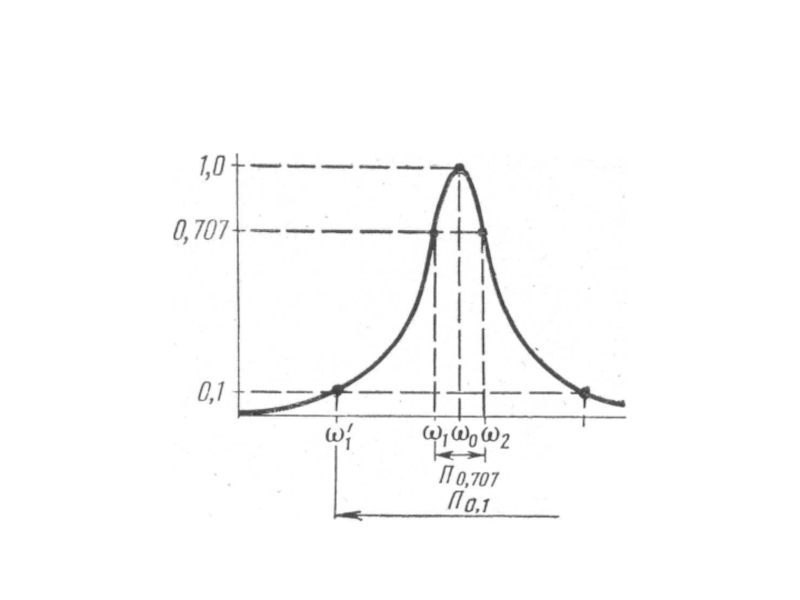
- 72. 5. Полоса пропускания ПКК Полосой пропускания последовательного
- 74. Разность граничных частот называется абсолютной полосой пропускания:
- 75. Отношение разности граничных частот к резонансной частоте называется относительной полосой пропускания:
- 77. 6. Коэффициент прямоугольности амплитудно-частотной характеристики Коэффициентом прямоугольности
- 78. коэффициент прямоугольности для последовательного колебательного контура
Л I Т Е Р А Т У Р А
1. Бондаренко В.Н. Основы теории цепей. К.: Институт электродинамики НАН Украины.-2012. с.313-329.
2. Карташов Р.П., Медведев А.П. Теория
Слайд 2Л I Т Е Р А Т У Р А 1. Бондаренко
В.Н. Основы теории цепей. К.: Институт электродинамики НАН Украины.-2012. с.313-329.
2. Карташов Р.П., Медведев А.П. Теория электрорадиоцепей,.
Слайд 31. Условия и признаки резонанса напряжений.
Последовательным колебательным контуром называют цепь, состоящую
из последовательного соединения индуктивности L и емкости С
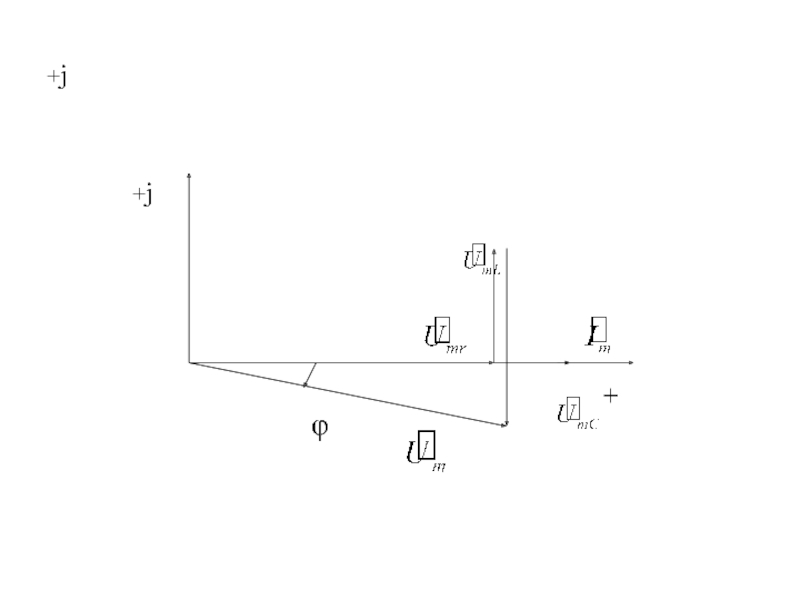
Слайд 11 При xL>xC сдвиг фаз между приложенным к цепи напряжением и током
в цепи φ>0, т.е. будет положительным, ток в цепи отстает от приложенного напряжения, цепь носит индуктивный характер (рис. 7.3)
Слайд 13
При xL
в цепи φ<0, т.е. будет отрицательным, ток в цепи опережает приложенное к ней напряжение. Цепь носит емкостной характер
Слайд 15
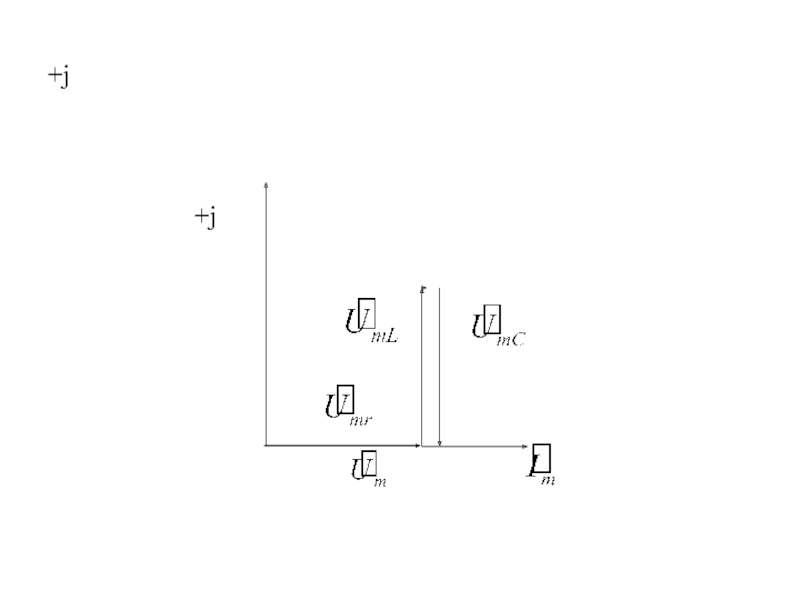
Наибольший интерес представляет случай равенства xL= xC. При этом реактивное сопротивление
контура равно нулю, комплексное сопротивление , цепь носит характер только активного сопротивления, ток в цепи совпадает по фазе с приложенным к ней напряжением.
Слайд 17
Уменьшение комплексного сопротивления контура до минимального приводит к возрастанию до максимума
тока в контуре, что свидетельствует о наступлении явления электрического резонанса. Существуют различные определения резонанса, взаимно дополняющие друг друга. Одно из них: резонансом (от латинского resono – откликаюсь) называется явление, при котором сопротивление контура становится только активным.
Слайд 18
Другое определение: резонансом называется резкое возрастание амплитуды вынужденных колебаний при приближении
частоты внешнего гармонического воздействия к частоте собственных колебаний контура. Равенство xL = xC является условием возникновения резонанса в последовательном колебательном контуре.
Слайд 19
При xL= xC сдвиг фаз между током и напряжением φ=0. В
этом случае хL=хLр; хС=хСр. По отношению к входным зажимам контур при резонансе эквивалентен цепи, состоящей из одного активного сопротивления r .
Слайд 20
Первый признак резонанса в последовательном колебательном контуре. Амплитуда тока в цепи
при резонансе принимает максимальное значение Im=Um/r . В остальных случаях амплитуда тока равна Im=Um/
Слайд 21
Второй признак резонанса напряжений в последовательном колебательном контуре. Напряжения на реактивных
элементах при резонансе равны по амплитуде и противоположны по фазе.
Слайд 22Учитывая то, что при резонансе xL = Xc,
можно записать, что
Учитывая
то, что при резонансе xL = Xc,
можно записать, что
можно записать, что
Слайд 232. Первичные и вторичные параметры последовательного колебательного контура.
Первичными параметрами последовательного
колебательного контура являются величина индуктивности L, величина емкости С и величина активного сопротивления r. Они характеризуют данный контур как совокупность конкретных элементов и позволяют отличить его от других контуров.
Слайд 24Рассмотрим, какие параметры относятся к вторичным
Резонансная частота контура -
это частота, при которой реактивное сопротивление контура равно нулю. Определим ее из равенства xL = xC :
Отсюда
Отсюда
Слайд 25
Это резонансная частота контура или частота собственных колебаний, которая определяется
только параметрами контура.
Слайд 26Волновое или характеристическое сопротивление контура.
Модули реактивных сопротивлений контура на резонансной частоте
равны и определяются как
Слайд 28Добротность контура
Резонансные свойства контура характеризуются добротностью контура. Добротностью контура называют
отношение напряжения на реактивном элементе (индуктивности или емкости) при резонансе к напряжению, действующему на входе контура
Слайд 29отношение волнового сопротивления контура к активному сопротивлению.
отношение волнового сопротивления контура
к активному сопротивлению.
Слайд 30
Добротность определяет эффективность или качество контура, является безразмерной величиной.
Чем меньше
активное сопротивление контура, тем выше его добротность. Для радиотехнических контуров характерны значения добротности от 100 до 500. Свойство контура усиливать приложенное напряжение широко используется на практике.
Величина, обратная добротности, носит название затухание контура
Величина, обратная добротности, носит название затухание контура
Слайд 31Это наименование параметра связано с тем,
что оно характеризует скорость затухания
колебаний
в контуре при отключении от него источника энергии.
в контуре при отключении от него источника энергии.
Это наименование параметра связано с тем,
что оно характеризует скорость затухания колебаний
в контуре при отключении от него источника энергии.
Слайд 323. Комплексні функції та частотні характеристики ПКК
Для анализа и описания частотно-избирательных
свойств колебательных контуров используют комплексные входные и передаточные функции. Наибольший интерес при изучении последовательных контуров представляют комплексная входная проводимость и комплексная передаточная функция по напряжению .
Слайд 33Комплексная входная проводимость:
Комплексной входной функцией цепи называется отношение комплексных амплитуд тока
и напряжения, действующих на входных зажимах.
Комплексная входная проводимость:
Слайд 343.1 Комплексная входная проводимость последовательного колебательного контура
Комплексная
входная проводимость последовательного колебательного контура рассчитывается через его параметры:
Слайд 37
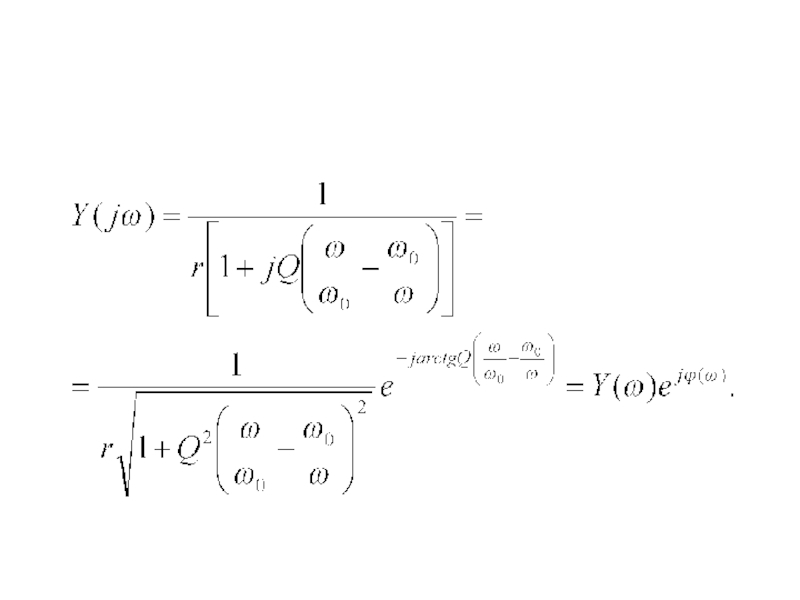
Нормированная комплексная входная проводимость получается путем отношения
к ее же значению при .
Так как , то
Так как , то
Слайд 39График нормированной входной АЧХ имеет следующий вид:
Увеличению добротности контура соответствуют
более острые
резонансные кривые или усиление
его частотно-избирательных свойств.
его частотно-избирательных свойств.
Слайд 40Зависимость аргумента проводимости контура от частоты называется фазо-частотной характеристикой
Слайд 41
Из этого графика следует, что на частотах ниже резонансной контур имеет
емкостной характер, при резонансе – резистивный, а на частотах выше резонансной – индуктивный.
Слайд 42
При исследовании частотных характеристик колебательного контура в качестве независимой переменной удобно
использовать величину, характеризующую расстройку контура, т.е. степень отклонения его резонансной частоты от частоты сигнала.
Слайд 43
Разность между частотой сигнала и резонансной частотой контура
называют абсолютной расстройкой.
Она может быть как положительной, так и отрицательной.
Слайд 44
Отношение абсолютной расстройки к резонансной частоте называется относительной расстройкой.
Слайд 46
Обобщенной расстройкой называют преобразованное отношение реактивного сопротивления контура к активному
Слайд 49
Относительная и обобщенная расстройки, как и фактор расстройки, безразмерные величины. Все
виды расстроек при резонансе равны нулю.
Преобразуя полученные формулы, получим выражения для нормированных частотных характеристик контура в функции расстройки:
Преобразуя полученные формулы, получим выражения для нормированных частотных характеристик контура в функции расстройки:
Слайд 52
3.2 Комплексная передаточная функция по напряжению .
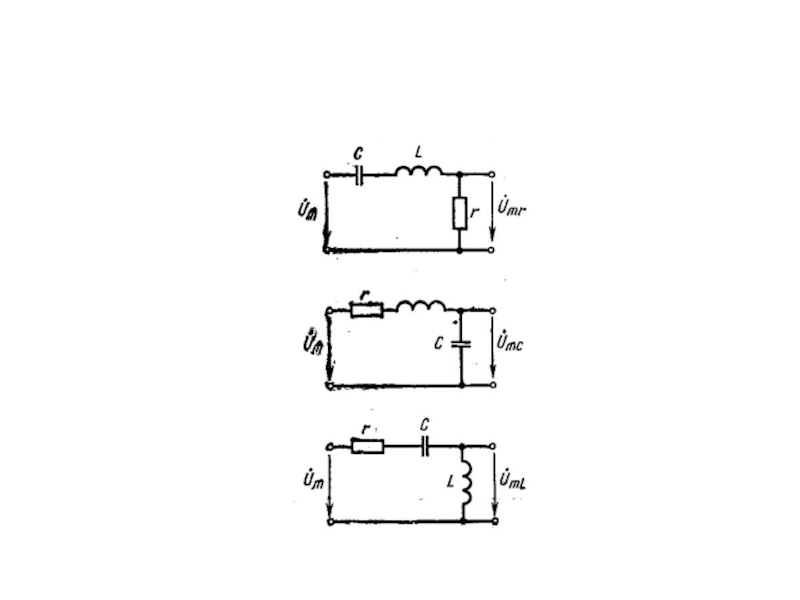
Комплексные передаточные функции по напряжению последовательного колебательного контура различают в зависимости от того, напряжение на каком из его элементов является выходным
Слайд 62 Численно передаточные функции, или коэффициенты передачи по напряжению, показывают, во сколько
раз напряжение на соответствующем элементе больше напряжения, действующего на входе контура. Из полученных соотношений, в частности, следует, что при резонансе напряжения на реактивных элементах в Q раз превышают входное напряжение, а напряжение на активном элементе равно ему.
Напряжение на реактивнх элементах достигает своего максимального значения в стороне от резонанса, а максимальные значения этих функций одинаковы.
Из всех комплексных коэффициентов передачи последовательного колебательного контура практический интерес представляет передаточная функция по напряжению на емкости, так как обычно выходное напряжение снимается с емкости.
Напряжение на реактивнх элементах достигает своего максимального значения в стороне от резонанса, а максимальные значения этих функций одинаковы.
Из всех комплексных коэффициентов передачи последовательного колебательного контура практический интерес представляет передаточная функция по напряжению на емкости, так как обычно выходное напряжение снимается с емкости.
Слайд 634. Резонансні характеристики ПКК
Резонансными характеристиками ПКК называют зависимость амплитуды тока в
контуре или напряжений на его элементах от частоты.
Слайд 64Рассмотрим эквивалентную комплексную схему замещения последовательного колебательного контура.
Слайд 69
При ток в цепи
равен нулю и напряжение на активном сопротивлении также равно нулю. Учитывая, что , при эта величина также равна нулю и амплитуда напряжения =0. Напряжение, приложенное к контуру, выделится на емкости, и .
Слайд 70
При частоте, равной резонансной, наблюдается равенство напряжений на реактивных элементах, однако
эти значения не максимальны. При изменении частоты в сторону уменьшения или увеличения от резонансной происходит незначительное вначале уменьшение тока, но за счет увеличения реактивных сопротивлений происходит рост напряжения на них.
Слайд 71
При
ток в цепи также равен нулю и напряжение на активном сопротивлении также равно нулю. Учитывая, что , при эта величина также равна нулю и амплитуда напряжения =0. Напряжение, приложенное к контуру, выделится на индуктивности, и .
Слайд 725. Полоса пропускания ПКК
Полосой пропускания последовательного колебательного контура называется диапазон частот
вблизи резонансной, на границах которого амплитуда тока в контуре снижается до уровня 0,707 своего максимального значения.
Слайд 75Отношение разности граничных частот к резонансной частоте называется относительной полосой пропускания:
Слайд 776. Коэффициент прямоугольности амплитудно-частотной характеристики
Коэффициентом прямоугольности резонансной кривой контура называется отношение
полосы пропускания контура, отсчитанной на
уровне , к полосе пропускания, отсчитанной на уровне :
уровне , к полосе пропускания, отсчитанной на уровне :
Слайд 78
коэффициент прямоугольности для последовательного колебательного контура является постоянной величиной, не зависящей
от его параметров:
