- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Будущее онтологии: Компьютерные универсумы презентация
Содержание
- 1. Будущее онтологии: Компьютерные универсумы
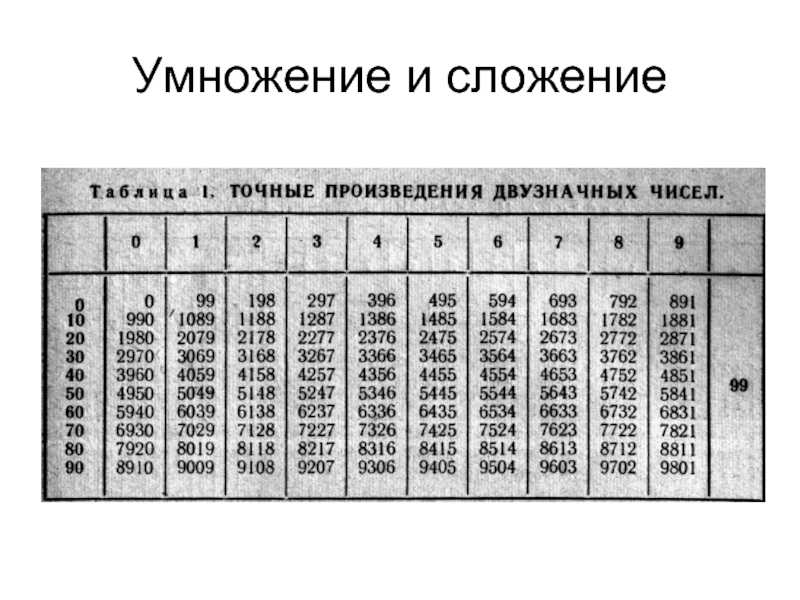
- 2. Умножение и сложение
- 3. МНР-машина (машина с неограниченными регистрами)
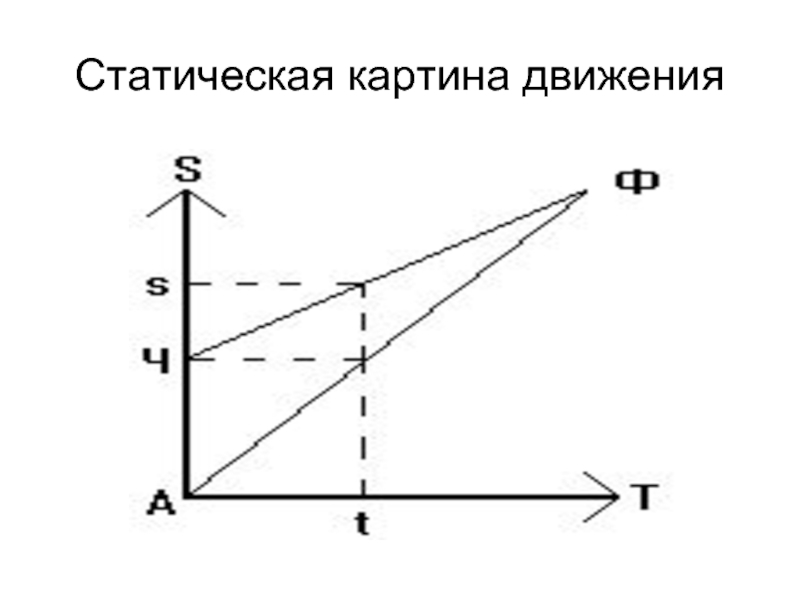
- 4. Статическая картина движения
- 5. Рассмотренное представление движения имеет статический характер.
- 6. Ряд сходится к 1
- 7. Г.Вейль: «Представим себе вычислительную машину, которая выполняла
- 8. Псевдорешение Здесь процесс движения, содержащий, по условию
- 9. Решение I. 1, 2, 3, …,
- 10. ABT-программы (π2) (π3) 1. CHOOSE X| X |= T 1. DELETE
- 11. DRIVING 0. CHOOSE X | X
- 12. Два типа времени
- 13. Метла времени
- 14. Аксиомы теории TS в языке LS
- 15. Программа BECOMING.ABT 1. DELETE X 2. CHOOSE X
Слайд 5
Рассмотренное представление движения имеет статический характер. Оно полностью подобно изображению движения
при помощи кинематографии. Как известно, изображение движения на киноленте складывается из отдельных кадров, на которых все неподвижно. Но если прокрутить эту ленту со скоростью 24 кадров в секунду, возникает иллюзия движения. Теперь представим себе, что количество кадров ленты несчетно, и что все они упорядочены так же, как и действительные числа, в результате чего каждому моменту времени соответствует один кадр. В итоге мы получим как раз ту картину движения, которая сводит его к сумме состояний покоя (отдельных кадров), расположенных непрерывным образом (в отличие от реальных кинолент). Но именно так и описывается движение в современной физике.
Слайд 7Г.Вейль:
«Представим себе вычислительную машину, которая выполняла бы первую операцию за 1/2
минуты, вторую - за 1/4 минуты, третью - за 1/8 минуты и т.д. Такая машина могла бы к концу первой минуты “пересчитать” весь натуральный ряд (написать, например, счетное число единиц). Ясно, что работа над конструкцией такой машины обречена на неудачу. Так почему же тогда тело, вышедшее из точки А, достигает конца отрезка В, “отсчитав” счетное множество точек А1, А2, ..., Аn,...?»
Слайд 8Псевдорешение
Здесь процесс движения, содержащий, по условию задачи, бесконечное число шагов, сводится,
по сути, к трём шагам: на шаге 1 вводится ряд точек 1/21, 1/22, 1/23, ..., 1/2n, ..., на шаге 2 постулируется, что Ахилл побывал в каждой из этих точек, а на шаге 3 делается вывод о завершении движения в конечной точке, не принадлежащей рассматриваемому ряду. В результате как бы “пересчитан” ряд, упорядоченный по типу ω+1. По видимости речь идет о бесконечном по числу шагов процессе, тогда как на деле процесс при таком подходе завершается за три шага.
Слайд 9Решение
I.
1, 2, 3, …, n, ………–n, …, –3, –2, –1
ω + ω*
II.
1, 2, 3, …, n, ………, N, ………,
где |N| = 2ω.
II.
1, 2, 3, …, n, ………, N, ………,
где |N| = 2ω.
Слайд 10ABT-программы
(π2) (π3)
1. CHOOSE X| X |= T 1. DELETE X
2. DELETE X 2. CHOOSE X| X |= T
3. GOTO
1 3. GOTO 1
(π4)
0. GOTO 1
1. CHOOSE X| X |= T
2. DELETE X
3. GOTO 1
Слайд 11DRIVING
0. CHOOSE X | X = tb
1. IF X =
Т' THEN END
2. CHOOSE Z | Z = f'(X)
3. CHOOSE Y | (Y отрезок Т') & Y=X+
4. DELETE X
5. DELETE Z
6. CHOOSE Z | Z = f'(Y)
7. IF Y = Т' THEN END
8. CHOOSE X | (X отрезок Т') & X = Y+
9. DELETE Y
10. DELETE Z
11. CHOOSE Z | Z = f'(X)
12. IF X = Т' THEN END
13. GOTO I3
2. CHOOSE Z | Z = f'(X)
3. CHOOSE Y | (Y отрезок Т') & Y=X+
4. DELETE X
5. DELETE Z
6. CHOOSE Z | Z = f'(Y)
7. IF Y = Т' THEN END
8. CHOOSE X | (X отрезок Т') & X = Y+
9. DELETE Y
10. DELETE Z
11. CHOOSE Z | Z = f'(X)
12. IF X = Т' THEN END
13. GOTO I3
Слайд 15Программа BECOMING.ABT
1. DELETE X
2. CHOOSE X | (X отрезок LD) & X
= Y+
3. IF X = LD THEN END
4. DELETE Y
5. CHOOSE Y | (Y отрезок LD) & Y = X+
6. IF Y = LD THEN END
7. DELETE X1
8. CHOOSE X1 | X1 ⎥= TS & X1 ‑ сужение в прошлое для Y1
9. DELETE Y1
10. CHOOSE Y1 | Y1 ⎥= TS* & Y1 ‑ переход в будущее относительно X1
11. DELETE X1
12. CHOOSE X1 | X1 ⎥= TS & X1 ‑ первое расширение в будущее для Y1
& X1 корректен & |Mm(X )| ≤ |Mm\(Mm(X) ∪ Mm(Y) ∪ Mm(X1) ∪ Mm(Y1))|
13. DELETE Y1
14. CHOOSE Y1 | Y1 ⎥= TS & Y1 ‑ второе расширение в будущее для X1
& Y1 корректен & |Mm(X1)| ≤ |Mm(Y1)|
15. GOTO 1
3. IF X = LD THEN END
4. DELETE Y
5. CHOOSE Y | (Y отрезок LD) & Y = X+
6. IF Y = LD THEN END
7. DELETE X1
8. CHOOSE X1 | X1 ⎥= TS & X1 ‑ сужение в прошлое для Y1
9. DELETE Y1
10. CHOOSE Y1 | Y1 ⎥= TS* & Y1 ‑ переход в будущее относительно X1
11. DELETE X1
12. CHOOSE X1 | X1 ⎥= TS & X1 ‑ первое расширение в будущее для Y1
& X1 корректен & |Mm(X )| ≤ |Mm\(Mm(X) ∪ Mm(Y) ∪ Mm(X1) ∪ Mm(Y1))|
13. DELETE Y1
14. CHOOSE Y1 | Y1 ⎥= TS & Y1 ‑ второе расширение в будущее для X1
& Y1 корректен & |Mm(X1)| ≤ |Mm(Y1)|
15. GOTO 1