- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Binary Tree. Проблема поиска значений презентация
Содержание
- 1. Binary Tree. Проблема поиска значений
- 2. Проблема поиска значений Коллекции (вроде массивов и
- 3. Проблема поиска значений Линейный поиск (как по
- 4. Решение проблемы поиска Если данных достаточно много,
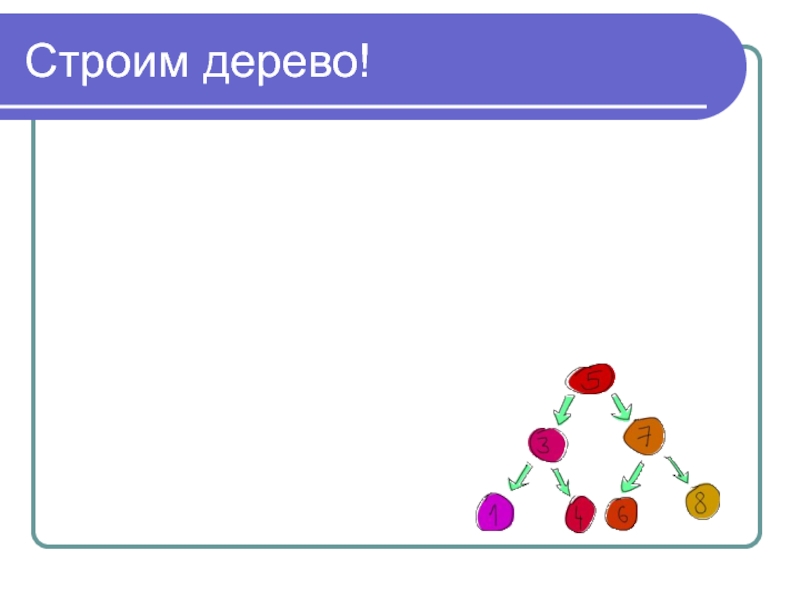
- 5. Строим дерево!
- 6. Определение понятия Дерево – это нелинейная структурированная
- 7. Виды деревьев Сбалансированные деревья K-мерные деревья R-дерево
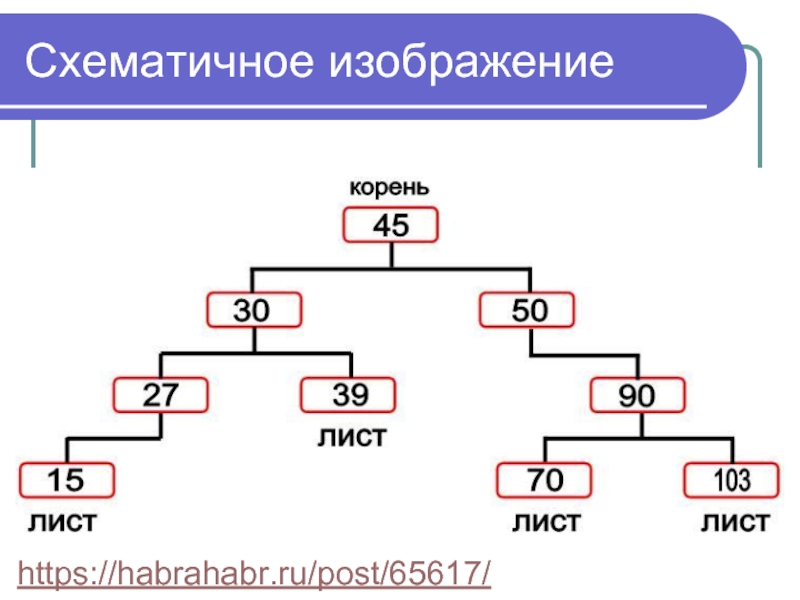
- 8. Схематичное изображение https://habrahabr.ru/post/65617/
- 9. Бинарное дерево Бинарное дерево – это частный
- 10. Бинарное дерево Левый потомок - дочерний узел
- 11. Строение одного узла дерева
- 12. Главный принцип Самый главный принцип бинарного дерева
- 13. Рекурсия передаёт привет ☺ Бинарное дерево является
- 15. Основные операции Поиск элемента Добавление элемента Распечатка
- 16. Класс элемента дерева class Node {
- 17. Распечатка дерева private void showTree(Node elem)
- 18. Подсчёт количества элементов private int getCount(Node elem,
- 19. Ключ – значение На практике, элементы деревьев
- 20. Реализация бинарного дерева Пример кода: https://git.io/vwsyd
Слайд 2Проблема поиска значений
Коллекции (вроде массивов и списков) позволяют хранить данные, а
также добавлять новые, удалять более ненужные, или редактировать уже существующие элементы. Однако, кроме всего этого, часто необходимо найти определённое значение в коллекции – и делается это, например, при помощи линейного либо бинарного поиска.
Слайд 3Проблема поиска значений
Линейный поиск (как по массиву, так и по списку)
может занять слишком много времени, в том случае если количество элементов в коллекции велико. Бинарный поиск требует, чтобы элементы коллекции были отсортированы, а определение медианы в списке – это явно не самый эффективный алгоритм...
Слайд 4Решение проблемы поиска
Если данных достаточно много, и приоритетной задачей является поиск
значений, тогда динамической структурой для хранения этих данных следует избрать дерево. Кроме того, почти так же, как и в списках, в деревьях эффективно реализуются добавление и удаление элементов.
Слайд 6Определение понятия
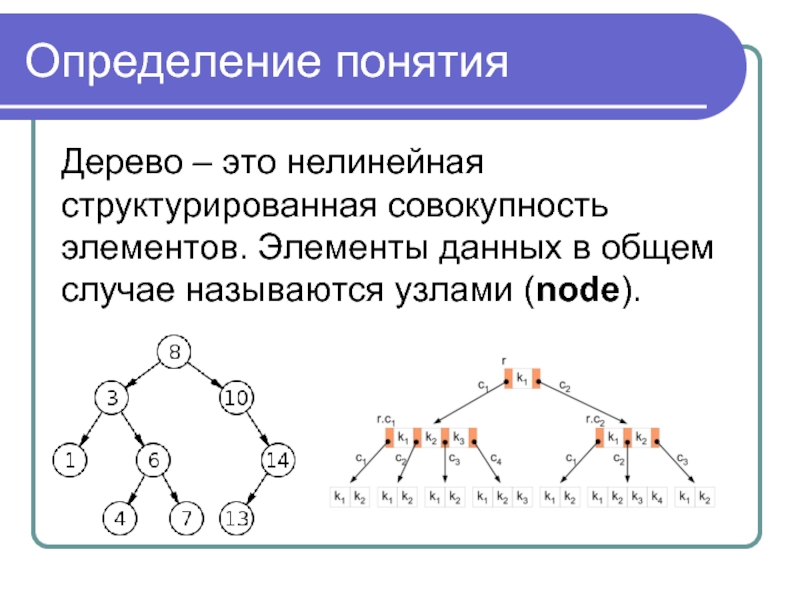
Дерево – это нелинейная структурированная совокупность элементов. Элементы данных в
общем случае называются узлами (node).
Слайд 7Виды деревьев
Сбалансированные деревья
K-мерные деревья
R-дерево
Кучи
Изящный граф-звезда
Двоичное (бинарное) дерево
Красно-чёрное дерево
Октодерево
Танцующее дерево и др.
Слайд 9Бинарное дерево
Бинарное дерево – это частный случай дерева, в котором каждый
узел имеет не более двух потомков (т.е. каждый узел может иметь 2, 1 или 0 потомков).
Узел, не имеющий потомков, называется листом (leaf).
Узел является родительским для своих потомков и дочерним для своего предка.
Узел, не имеющий потомков, называется листом (leaf).
Узел является родительским для своих потомков и дочерним для своего предка.
Слайд 10Бинарное дерево
Левый потомок - дочерний узел слева от текущего узла.
Правый
потомок - дочерний узел справа от текущего узла.
Корень – это основной узел (добавляется в дерево первым), не имеющий родителя.
Каждый узел состоит из четырех частей:
Значение.
Указатель на родителя.
Указатель на левого потомка.
Указатель на правого потомка.
Корень – это основной узел (добавляется в дерево первым), не имеющий родителя.
Каждый узел состоит из четырех частей:
Значение.
Указатель на родителя.
Указатель на левого потомка.
Указатель на правого потомка.
Слайд 12Главный принцип
Самый главный принцип бинарного дерева заключается в том, что для
каждого узла выполняется правило: в левой ветке содержатся только те ключи, которые имеют значения, меньшие, чем значение данного узла. В правой же ветке содержатся ключи, имеющие значения, большие, чем значение данного узла.
Слайд 13Рекурсия передаёт привет ☺
Бинарное дерево является рекурсивной структурой, поскольку каждое его
поддерево само по себе является бинарным деревом, и, следовательно, каждый его узел в свою очередь является корнем самостоятельного дерева. Поэтому, при работе с деревьями обычно используются рекурсивные алгоритмы.
Слайд 15Основные операции
Поиск элемента
Добавление элемента
Распечатка данных
Изменение значения элемента
Удаление элемента
Подсчёт количества элементов
Очистка дерева
Слайд 16Класс элемента дерева
class Node { // inner class!
private int value;
private Node parent;
private Node right;
private Node left;
public int getValue() {
return value;
}
}
private Node parent;
private Node right;
private Node left;
public int getValue() {
return value;
}
}
Слайд 17Распечатка дерева
private void showTree(Node elem) {
if (elem
!= null) {
showTree(elem.left);
System.out.print(elem.getValue());
showTree(elem.right);
}
}
showTree(elem.left);
System.out.print(elem.getValue());
showTree(elem.right);
}
}
Слайд 18Подсчёт количества элементов
private int getCount(Node elem, int count) {
if
(elem != null) {
count = getCount(elem.left, count);
count++;
count = getCount(elem.right, count);
}
return count;
}
count = getCount(elem.left, count);
count++;
count = getCount(elem.right, count);
}
return count;
}
Слайд 19Ключ – значение
На практике, элементы деревьев чаще всего хранят не просто
одно лишь значение, а пару «ключ - значение». В качестве ключа обычно выступает целое число или строка, в то время как значением может быть список, любая другая коллекция, или объект пользовательского типа.