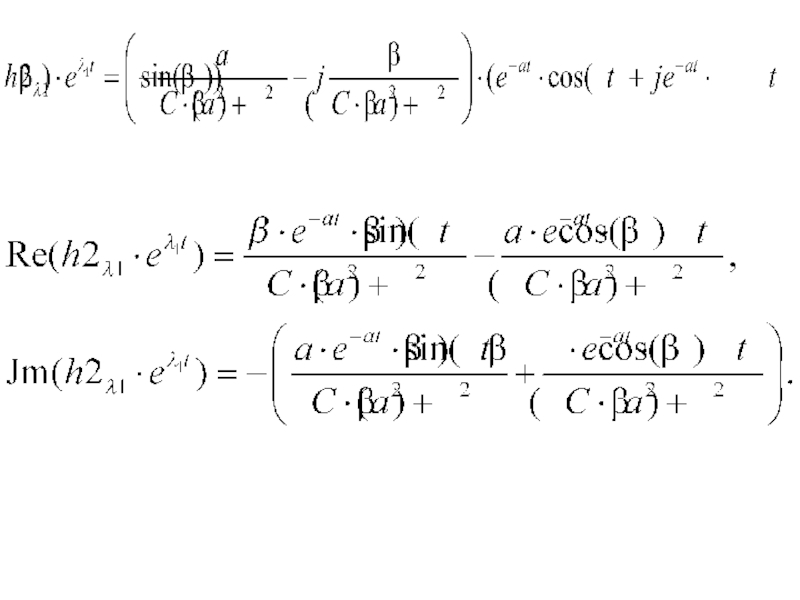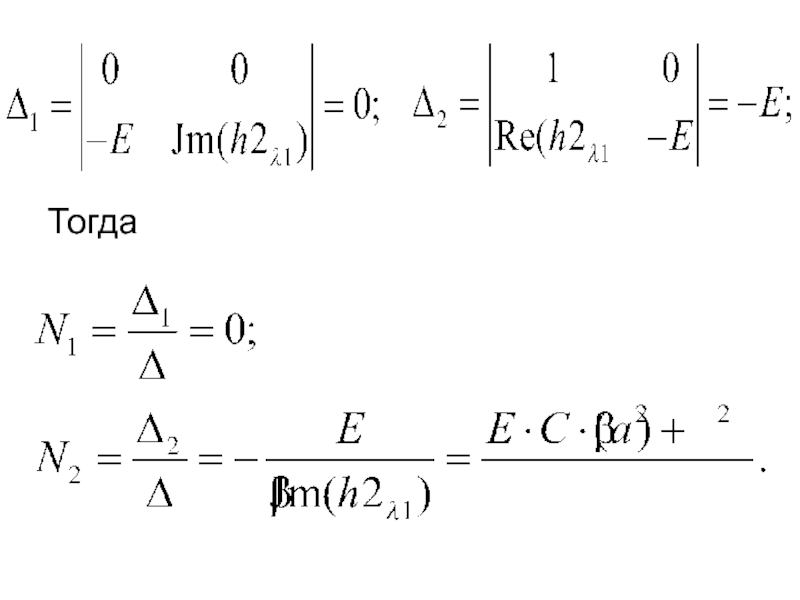- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Анализ процессов в электромеханических системах классическим методом презентация
Содержание
- 1. Анализ процессов в электромеханических системах классическим методом
- 2. Три метода Решение систем дифференциальных
- 3. Решения системы дифференциальных уравнений на примере RLC-цепи
- 4. Составим Систему Дифференциальных Уравнений, описывающую процессы в данной цепи.
- 5. Представим СДУ в нормальной форме Коши:
- 6. Запишем СДУ в матричной форме:
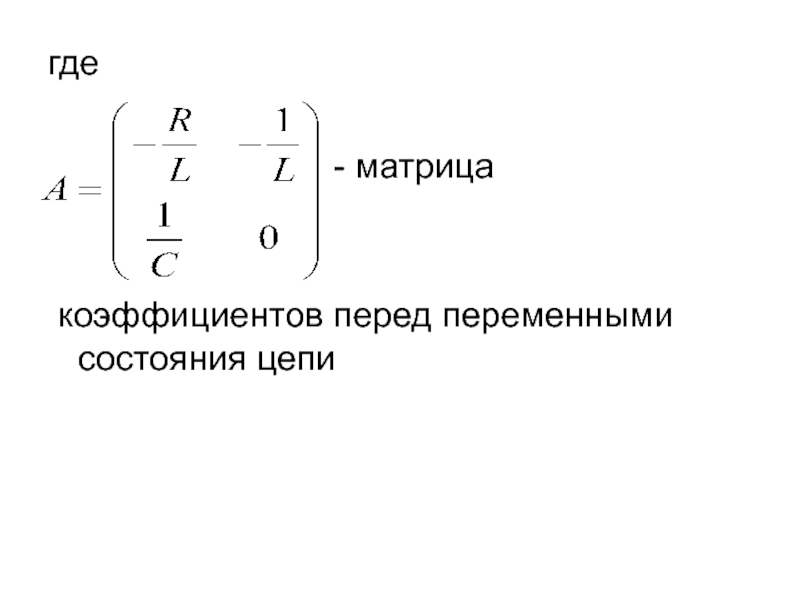
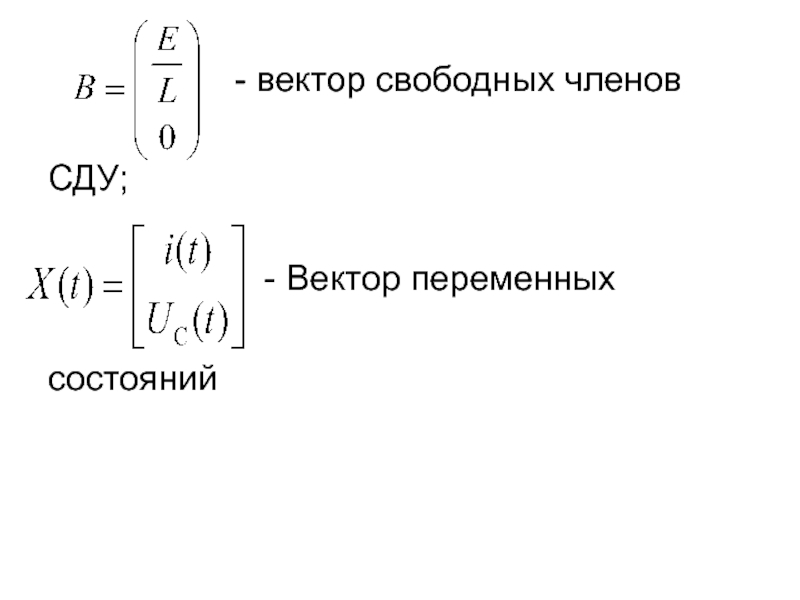
- 7. где
- 9. Определение корней СДУ Запишем однородную СДУ в виде:
- 10. Составим характеристическое уравнение введем обозначения
- 11. Тогда характеристическое уравнение можно записать в виде:
- 12. Предположим, что корни характеристического уравнения действительные и
- 13. Найдем собственные вектора для каждого собственного значения
- 14. или Примем значение
- 15. Собственный вектор для первого собственного значения
- 16. Общее решение однородной
- 17. Можно записать
- 18. Предположим, что корни характеристического уравнения ком- плексно
- 19. Принимаем h1λ1 =1 и находим h2λ1 из второго уравнения системы:
- 20. Общее решение однородной СДУ в этом случае запишется в виде:
- 21. Запишем каждую компоненту общего решения отдельно:
- 22. Найдем составляющие общего решения однородной СДУ. По формуле Эйлера для комплексных чисел:
- 23. тогда Для разделения вещественной
- 24. Учитывая формулу умножения комплексно сопряженных чисел друг на друга, запишем:
- 26. Общее решение однородной СДУ:
- 27. Вывод Сравнивая результаты общего решения
- 28. Частное решение СДУ Найдем частное решение неоднородной
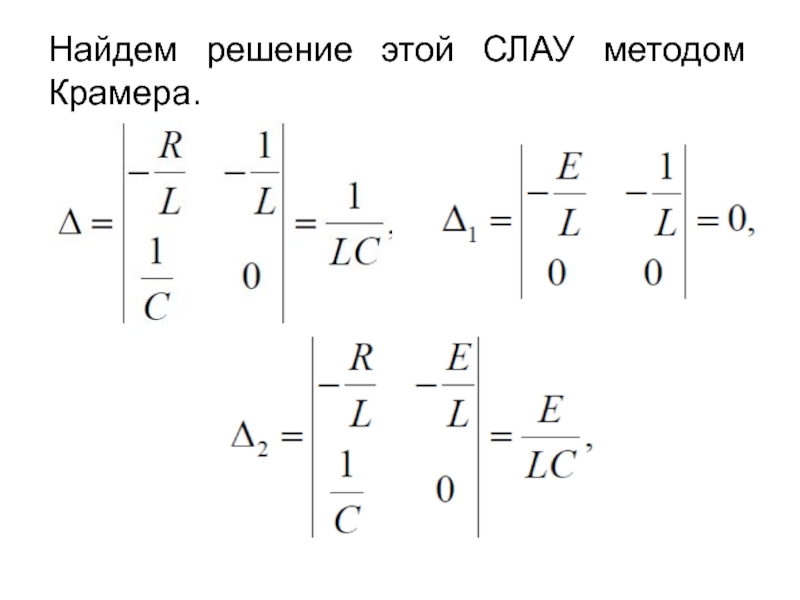
- 29. Найдем решение этой СЛАУ методом Крамера.
- 30. Тогда получим Полученное частное решение неоднородной СДУ
- 31. Этапа определения постоянных интегрирования Нахождение постоянных интегрирования
- 32. Действительные отрица- тельные корни Найдем постоянные
- 34. При t = 0 и нулевых
- 35. Перенесем свободные члены: Решим эту СЛАУ методом Крамера:
- 37. тогда Запишем компоненты общего решения неоднородной СДУ: - для тока
- 38. для напряжения на емкости
- 39. Комплексные сопряженные корни Определим постоянные интегрирования при
- 40. Общее решение неоднородной СДУ
- 41. При t = 0 и нулевых начальных
- 42. Решим эту СЛАУ методом Крамера:
- 43. Тогда
- 44. Запишем компоненты общего решения СДУ:
Три метода Решение систем дифференциальных уравнений и соответственно анализ процессов в электромеханических системах осуществляют с использованием трех методов: Классический метод; Операторный метод; Метод переменных состояний.
Слайд 2Три метода
Решение систем дифференциальных уравнений и соответственно анализ процессов
в электромеханических системах осуществляют с использованием трех методов:
Классический метод;
Операторный метод;
Метод переменных состояний.
Классический метод;
Операторный метод;
Метод переменных состояний.
Слайд 3Решения системы дифференциальных
уравнений на примере RLC-цепи
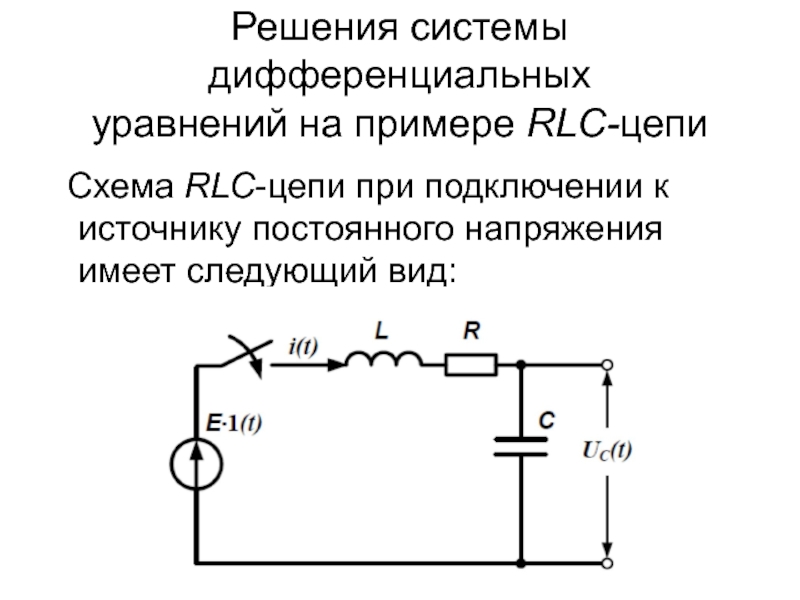
Схема RLC-цепи при подключении к
источнику постоянного напряжения имеет следующий вид:
Слайд 11Тогда характеристическое уравнение можно записать в виде:
Решение этого уравнения имеет
следующий вид
Слайд 12Предположим, что корни характеристического уравнения действительные и разные:
Отметим,
что для устойчивости динамической системы необходимо, чтобы действительные части корней характеристического уравнения были отрицательными.
Слайд 13Найдем собственные вектора для каждого собственного значения матрицы A.
Для значения λ1
= −a алгебраическая система уравнений будет выглядеть следующим образом:
Слайд 15
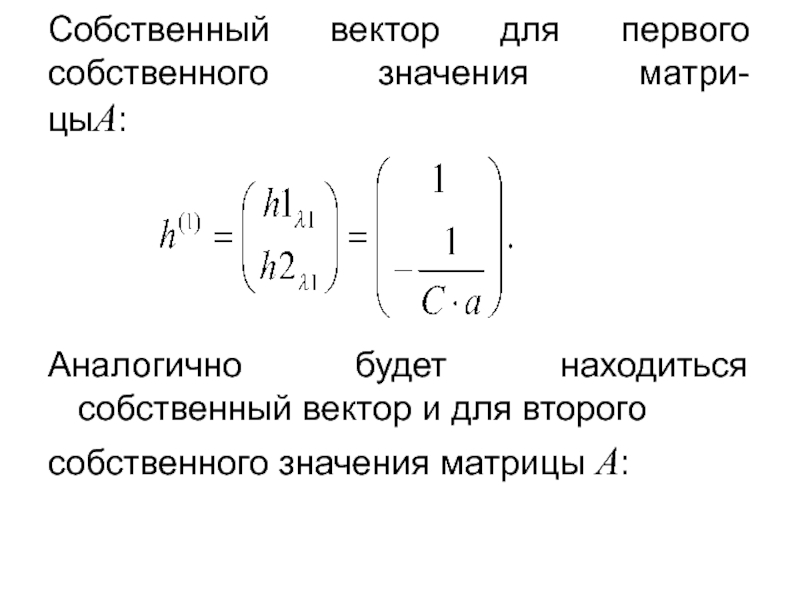
Собственный вектор для первого собственного значения матри-
цыA:
Аналогично будет находиться собственный вектор
и для второго
собственного значения матрицы A:
собственного значения матрицы A:
Слайд 18Предположим, что корни характеристического уравнения ком-
плексно сопряженные:
В этом случае собственный вектор
ищется только для одного из этих значений.
Найдем собственный вектор для
λ1 = −α + jβ :
Найдем собственный вектор для
λ1 = −α + jβ :
Слайд 23тогда
Для разделения вещественной и мнимой частей второй составляющей h2λ1 собственного вектора
домножим числитель и знаменатель h2λ1 на число, комплексно сопряженное знаменателю
h2 λ1 :
h2 λ1 :
Слайд 27Вывод
Сравнивая результаты общего решения однородной СДУ при действительных и
комплексно сопряженных корнях, можно отметить, что в первом случае переходные процессы в ЭМС имеют апериодический характер, а во втором случае – затухающий колебательный.
Слайд 28Частное решение СДУ
Найдем частное решение неоднородной СДУ при подстановке в исходную
СДУ значения t = ∞ :
Слайд 30Тогда получим
Полученное частное решение неоднородной СДУ легко объясняется физически – конденсатор
заряжается до напряжения источника питания E, а ток в цепи после окончания переходного процесса становится
равным нулю, так как при работе на постоянном токе конденсатор представляет собой разрыв цепи.
равным нулю, так как при работе на постоянном токе конденсатор представляет собой разрыв цепи.
Слайд 31Этапа определения постоянных интегрирования
Нахождение постоянных интегрирования осуществляют путем подстановки в общее
решение неоднородной СДУ значения t = 0 и последующего решения получившейся СЛАУ.
Решим задачу Коши для обоих случаев собственных значений матрицы A – действительных и комплексно сопряженных
Решим задачу Коши для обоих случаев собственных значений матрицы A – действительных и комплексно сопряженных
Слайд 32Действительные отрица-
тельные корни
Найдем постоянные интегрирования при действительных отрицательных собственных значениях
матрицы A:
λ1 = −a, λ2 = −b .
Общее решение неоднородной СДУ в этом случае имеет вид
λ1 = −a, λ2 = −b .
Общее решение неоднородной СДУ в этом случае имеет вид
Слайд 34 При t = 0 и нулевых начальных условиях, то есть
i (0) = 0, UC (0) =0 . Запишем получившуюся СЛАУ:
Слайд 39Комплексные сопряженные корни
Определим постоянные интегрирования при комплексно сопряженных корнях характеристического уравнения:
λ1,2 = −α ± jβ.
Общее решение неоднородной СДУ имеет в этом случае следующий вид:
Слайд 41При t = 0 и нулевых начальных условиях, то есть i
(0) = 0, UC (0) =0 . Запишем получившуюся СЛАУ
Перенесем свободные члены, а также учтем, что h1λ1 = 1 и Re(h1λ 1 ) = 1 , Jm(h1λ1 ) = 0, тогда получим систему линейных дифференциальных уравнений в виде:
