- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
А презентация
Содержание
- 1. А
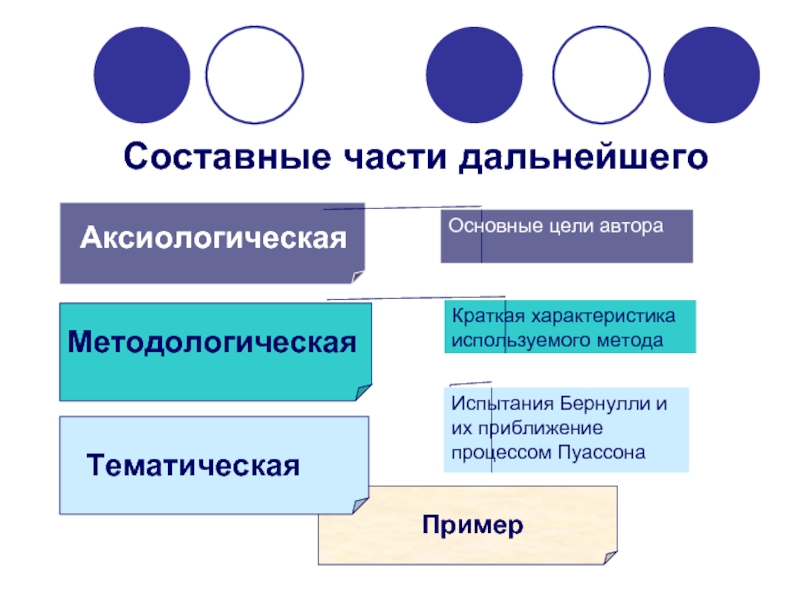
- 2. Составные части дальнейшего
- 3. 2. Является ли «Прикладная физика» научной специальностью
- 4. Университет как высшее учебно-научное заведение Университет
- 5. Ответ на риторический вопрос
- 6. НАУКА ЛИ ПРИКЛАДНАЯ ФИЗИКА ? ТАКОЙ
- 7. НАУКА ЛИ ПРИКЛАДНАЯ ФИЗИКА ? История формирования
- 8. Методология прикладной физики и методология физики
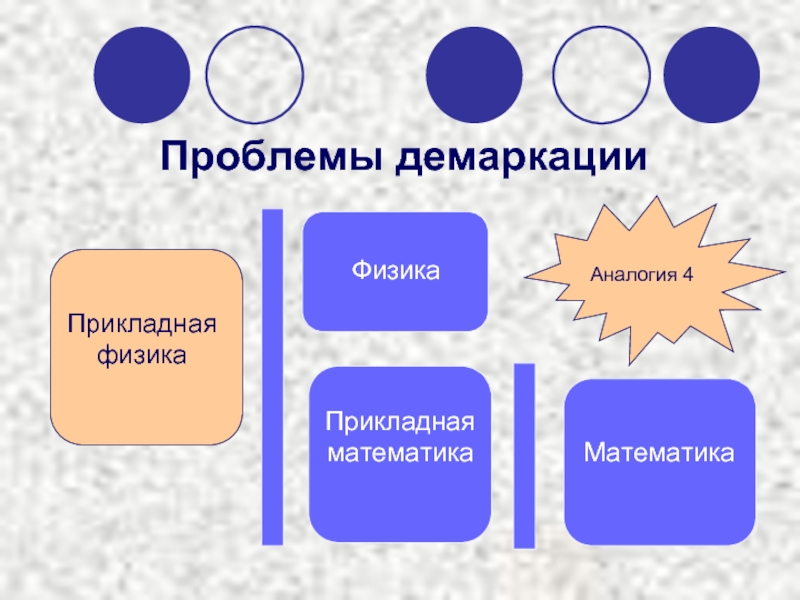
- 9. Проблемы демаркации
- 10. Целевая направленность физики и прикладной
- 11. 1-й уровень взаимодействия технических наук и прикладной
- 12. ХАРАКТЕРНЫЕ ОСОБЕННОСТИ РАЦИОНАЛЬНЫХ РАССУЖДЕНИЙ Применение формулировок, включающих
- 13. Схема испытаний Бернулли На дне глубокого
- 14. Определение испытаний Бернулли Дано: 1. Некоторое испытание
- 15. 1. Вероятность того, что в n испытаниях
- 16. Испытания Бернулли как процесс
- 17. Уравнение Чепмена-Колмогорова
- 18. Общее уравнение для плотности вероятности
- 19. Конкретизация вида уравнения для плотности вероятности
- 20. Конкретизация вида уравнения для плотности вероятности
- 21. О двух способах конкретизации вида
- 22. Реализация одного из способов
- 23. К сравнению способов конкретизации вида уравнения для
- 24. Доклад закончен. Благодарю за внимание
Слайд 1Бранспиз Ю.А.
Восточноукраинский национальный университет имени Владимира Даля
А
П
П
Ф
2008
Процесс
Пуассона
как
универсальный вероятностный
процесс
Слайд 32. Является ли «Прикладная физика»
научной специальностью ?
1. «Законно» ли существование кафедр
Аксиологическая часть
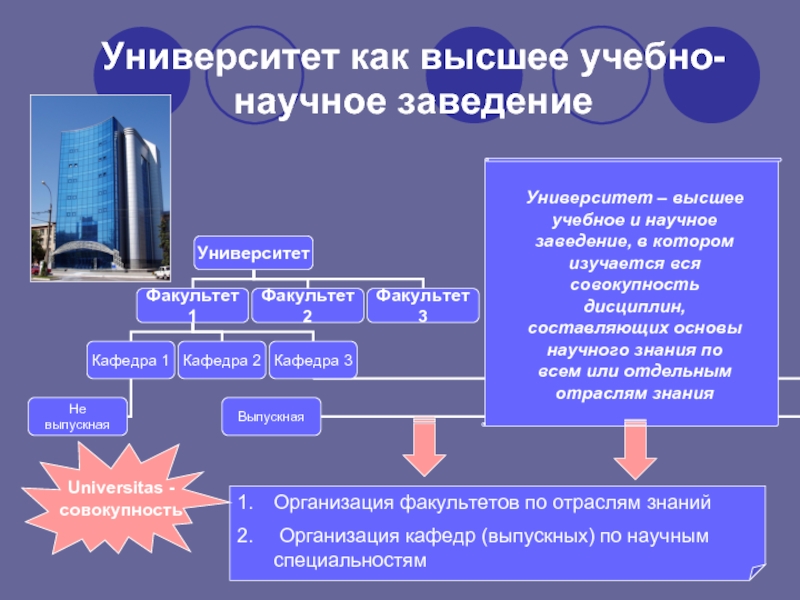
Слайд 4Университет как высшее учебно-научное заведение
Университет – высшее учебное и научное заведение,
Universitas - совокупность
Слайд 6НАУКА ЛИ ПРИКЛАДНАЯ ФИЗИКА ?
ТАКОЙ ВОТ ВОПРОС
Пожалуй вопросом «что такое философия»
Ж. Делез, Ф. Гваттари
Слайд 7НАУКА ЛИ ПРИКЛАДНАЯ ФИЗИКА ?
История формирования технических наук
1. Описание природных процессов
2. Такое изменение реального объекта, которое полностью соответствует теории.
3. Перевод техническим путем реального объекта в идеальное состояние на основе использования открытых теорией законов природы – в целях практики.
Реализация замысла: на основе теории – запустить реальный природный процесс в техническом устройстве , сделав его следствием человеческой деятельности.
Г. Галилей
Х. Гюйгенс
Слайд 8Методология прикладной физики
и методология физики
1. В процессе схематизации (формализации) решаемых
Общее и различие :
2. В процессе замещения реального процесса (явления) математической моделью.
3. В процессе формирования новых теоретических знаний .
4. В характере теоретических знаний и организации их использования
Слайд 10
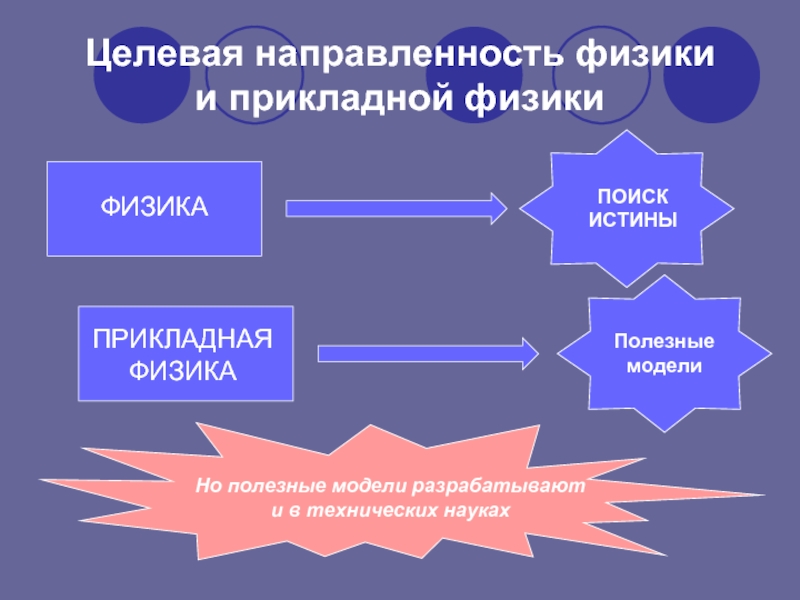
Целевая направленность физики
и прикладной физики
ПРИКЛАДНАЯФИЗИКА
Полезные модели
Но полезные модели разрабатывают и
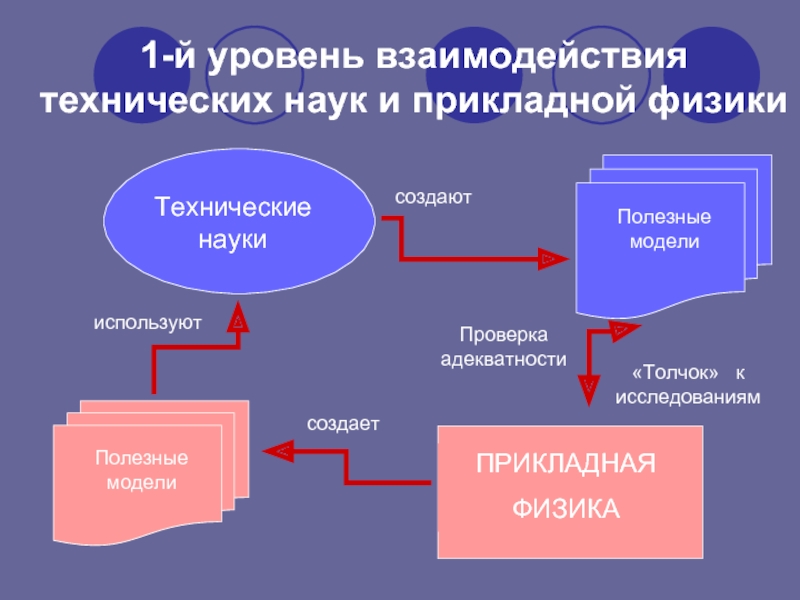
Слайд 111-й уровень взаимодействия технических наук и прикладной физики
Технические науки
создают
используют
создает
Проверка адекватности
«Толчок»
исследованиям
Слайд 12ХАРАКТЕРНЫЕ ОСОБЕННОСТИ
РАЦИОНАЛЬНЫХ РАССУЖДЕНИЙ
Применение формулировок, включающих неточно определенные понятия
Применение утверждений, допускающих частные
Уточнение в ходе исследования (открытость для уточнения)
Использование аналогий и соответствия
Использование доводов, основанных на частных данных экспериментов
Моделирования дискретного континуумом и континуума дискретностью
Применение практической бесконечности (знаки>> и << )
Интерполяция и экстраполяция результатов
Блехман И.И., Мышкис А.Д., Пановко Я.Г. Прикладная математика: предмет, логика, особенности подходов.– Киев: Наукова думка, 1976.
Слайд 13Схема испытаний Бернулли
На дне глубокого сосуда
Лежат спокойно n шаров.
Поочередно их
Таскают двое дураков.
Сия работа им приятна,
Они таскают t минут,
И, вынув шар, его обратно
Тотчас немедленно кладут.
Ввиду занятия такого,
Сколь вероятность велика,
Что первый был глупей второго,
когда шаров он вынул k?
В.П. Скитович
Слайд 14Определение испытаний Бернулли
Дано:
1. Некоторое испытание (физический процесс).
2. В результате испытания событие
3. Вероятность события S в каждом из испытаний не зависит от результата остальных испытаний и равна p.
4. Осуществление события S – «успех», не осуществление – «неудача».
Пример: 1. S – изменение некоторого параметра в системе многих частиц в сторону увеличения («успех) или уменьшения («неудача»); каждое такое изменение – испытание Бернулли.
2. Увеличение некоторого параметра в системе многих частиц на величину менее («успех») или более («неудача») данной.
Слайд 151. Вероятность того, что в n испытаниях Бернулли событие S произойдет
где - число сочетаний из n по k.
,
2. Пусть n стремится к бесконечности и p→0. Пусть также имеет место предел np→λ>0. Тогда для любого k>0 вероятность получить k «успехов» в n испытаниях схемы Бернулли с вероятностью успеха p стремится к величине
То есть, имеет место предельный переход
Закономерности испытаний Бернулли
Слайд 16
Испытания Бернулли
как процесс Пуассона
Определение процесса Пуассона:
.
Эту вероятность можно
Для любого физического процесса всегда можно подобрать соответствующий вид зависимости !
Слайд 18
Общее уравнение
для плотности вероятности изменения значения параметра х
Применяя к
разложения в ряд Тейлора получим
(ОУПВ)
Слайд 20Конкретизация вида уравнения
для плотности вероятности изменения значения параметра
2
Ограничение числа
характеристиками изменения параметра х: и
Порядок малости
не может превышать порядок малости величины ,
Слайд 23К сравнению способов конкретизации вида уравнения для плотности вероятности случайного изменения
1-й способ описания (процесс Пуассона)
2-й способ описания
(диффузия с дрейфом)
Соответствующим подбором соотношений констант, характеризующих два способа описания случайного изменения параметра х , можно добиться, что средние и дисперсии этих способов будут одинаковы