- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: Заряд и его свойства, закон Кулона (продолжение) презентация
Содержание
- 1. Тема: Заряд и его свойства, закон Кулона (продолжение)
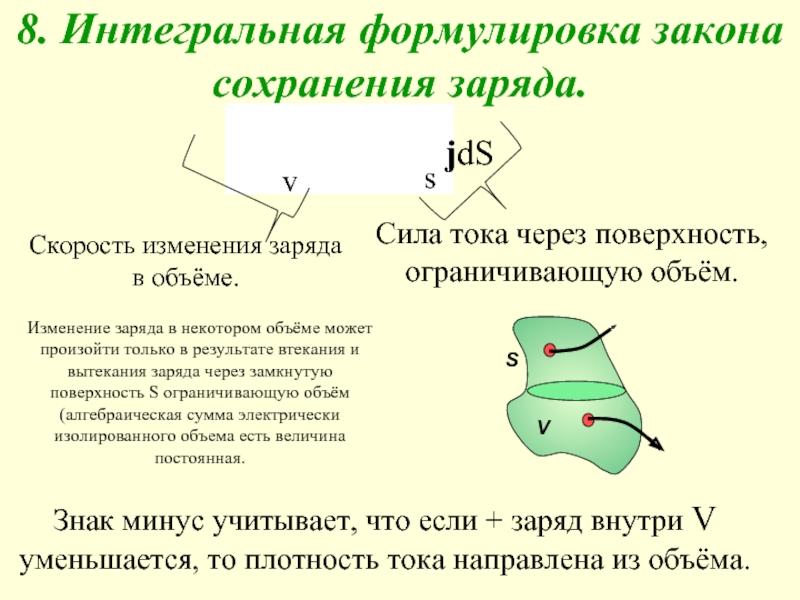
- 2. 8. Интегральная формулировка закона сохранения заряда. jdЅ
- 3. 9. Дифференциальная формулировка закона сохранения заряда.
- 4. Запишем данное выражение в виде (это связь
- 5. Сравнивая подинтегральные выражения в формуле (1), видим,
- 6. 10. Сохранение заряда в 4-х мерном пространстве
- 7. Легко видеть, что изменение плотности заряда во
- 8. Это и есть закон сохранения заряда в
- 9. Закон Кулона. q1,q2 –
- 11. 9 На каждый заряд, действуют по 3 силы Q F
- 12. Сущность модели электростатического поля Важна
- 13. Детектор поля – точечный заряд.
- 14. Согласно принципу суперпозиции электрическое поле системы зарядов равно векторной сумме напряженностей полей, создаваемых отдельными зарядами
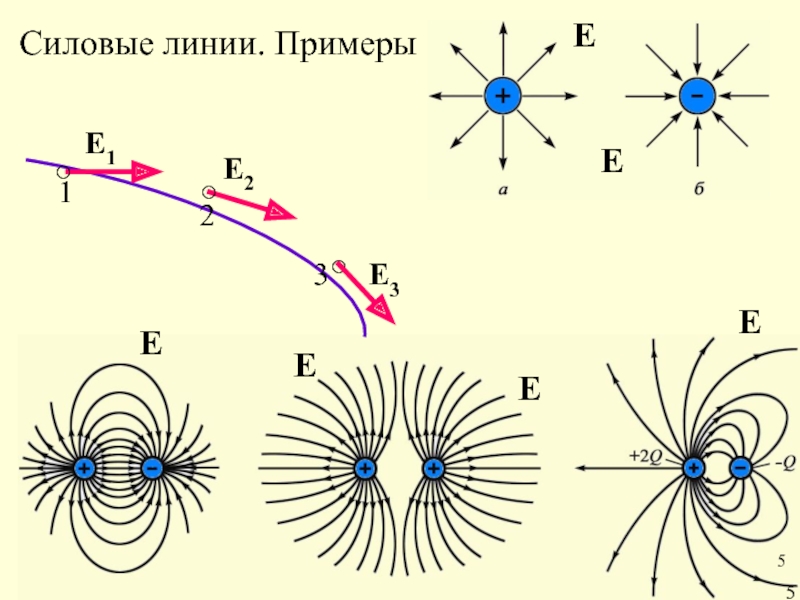
- 15. Силовые линии. Примеры 5 Е Е Е Е Е Е 5
- 16. ● dy σ ●
- 17. Справедлив принципы суперпозиции: Вектор электрического
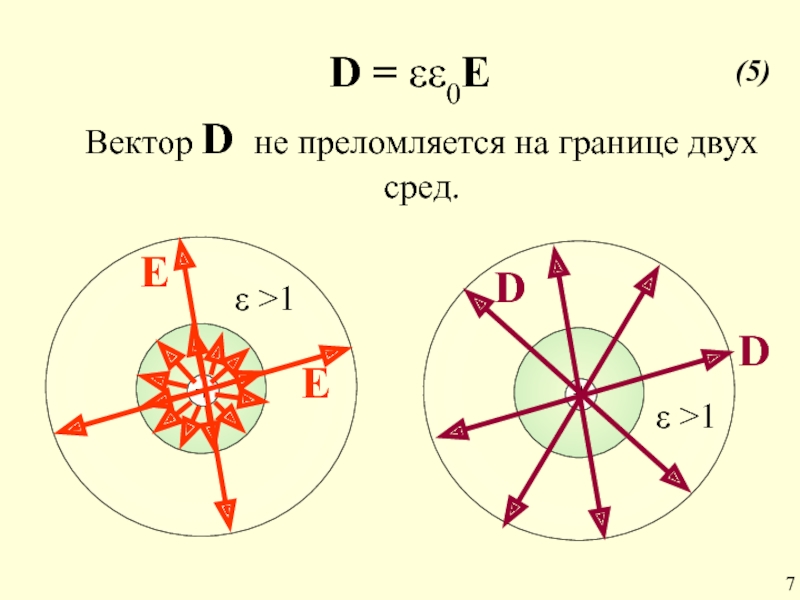
- 18. + ε >1
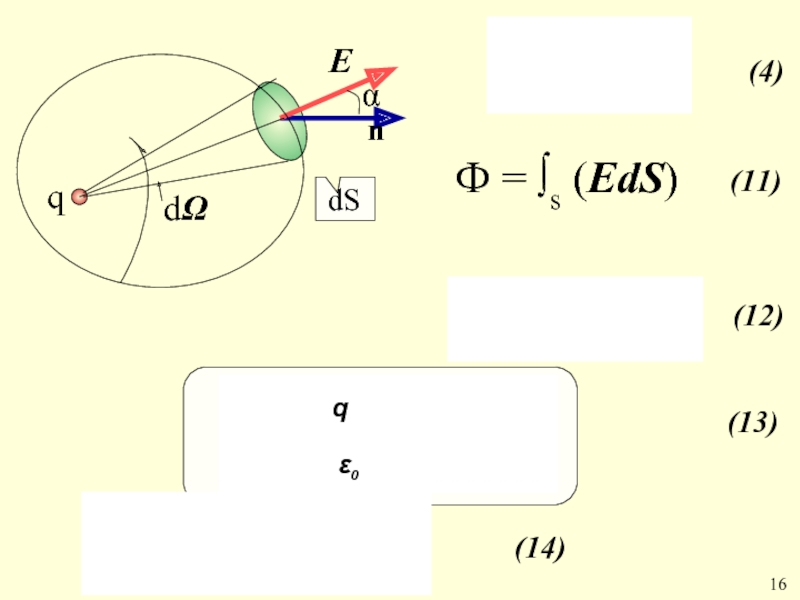
- 19. Поток вектора (
- 20. Ф через искривлённую поверхность Ф = ∫s
- 21. Теорема Гаусса (закон Гаусса) Закон Гаусса
- 22. 16 (4) (11) (12)
- 23. ∫ ○ dΩ=4π Если зарядов в объёме
- 24. Если заряд находится вне объёма:
- 25. Физической основой ТОГ является закон Кулона, поэтому теорема Гаусса является интегральной формулировкой закона Кулона. 19
- 26. Поток вектора напряженности сквозь произвольную замкнутую поверхность
- 27. Применение теоремы Гаусса. По тонкой сферической
- 28. Вектор Е направлен радиально в
- 29. На пов-ти сферы т.к. S
- 30. 25 + + +
- 31. Поле Е равномерно заряженной ∞ нити
- 32. Электрическое поле Е бесконечно большой заряженной плоскости
Слайд 28. Интегральная формулировка закона сохранения заряда.
jdЅ
s
v
Изменение заряда в некотором объёме может
Скорость изменения заряда в объёме.
Сила тока через поверхность, ограничивающую объём.
Знак минус учитывает, что если + заряд внутри V уменьшается, то плотность тока направлена из объёма.
Слайд 3
9. Дифференциальная формулировка закона сохранения заряда.
Итак интеграл по поверхности равен интегралу
Слайд 4Запишем данное выражение в виде (это связь интеграла по поверхности с
(1)
Здесь дивергенция равна
Слайд 5Сравнивая подинтегральные выражения в формуле (1), видим, что
Это и есть закон
Слайд 610. Сохранение заряда в 4-х мерном пространстве
Перепишем выражение для дивергенции и
Слайд 7Легко видеть, что изменение плотности заряда во времени можно представить как
Окончательно:
Слайд 8Это и есть закон сохранения заряда в дифференциальной форме для 4-х
Преобразование из К системы в систему К’ для одномерного тока jx и плотности заряда ρ в СТО имеет вид:
Слайд 9
Закон Кулона.
q1,q2 – точечные заряды; r – расстояние между
Принцип суперпозиции:
(1)
(2)
3
Слайд 12 Сущность модели
электростатического поля
Важна не неподвижность зарядов, а постоянство во
Границы применимости – требование малости вклада от отдельных зарядов в наблюдаемое поле.
Основная задача электростатики: найти
поля, создаваемые «неподвижными» зарядами
2
Слайд 13
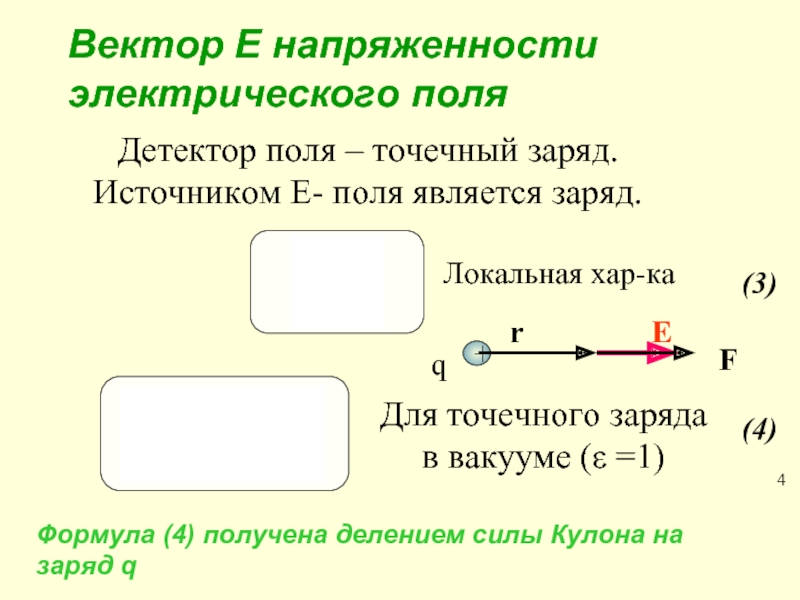
Детектор поля – точечный заряд.
Источником Е- поля является заряд.
Для точечного
в вакууме (ε =1)
(3)
(4)
4
Локальная хар-ка
+
q
E
r
F
Вектор Е напряженности электрического поля
Формула (4) получена делением силы Кулона на заряд q
Слайд 14Согласно принципу суперпозиции электрическое поле системы зарядов равно векторной сумме напряженностей
Слайд 16●
dy
σ
●
z
А
y
x
+
+
+
+
+
+
+
+
+
+
+
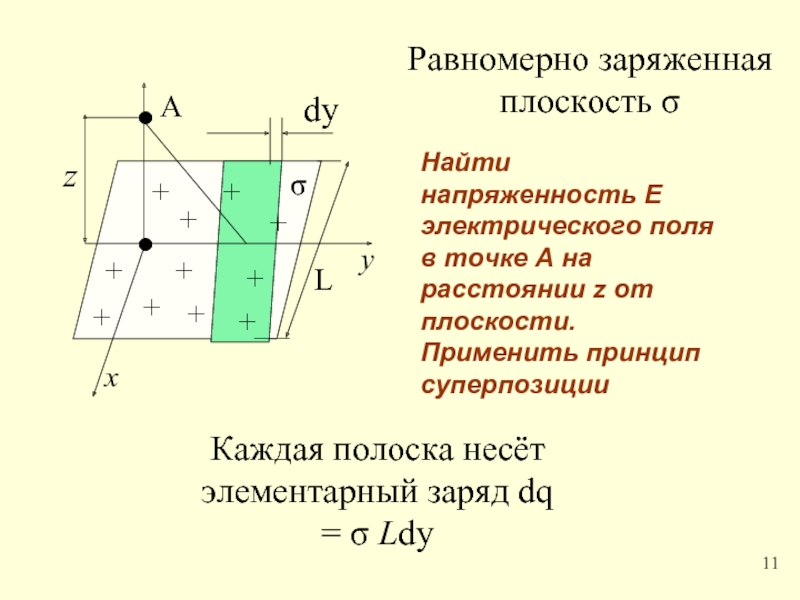
Равномерно заряженная плоскость σ
L
Каждая полоска несёт элементарный заряд dq =
11
Найти напряженность Е электрического поля в точке А на расстоянии z от плоскости. Применить принцип суперпозиции
Слайд 17
Справедлив принципы суперпозиции:
Вектор электрического смещения (вектор индукции
D = εε0E
Формула для однородной среды. Вектор направлен также как и Е.
6
(5)
(6)
(7)
Для точечного заряда
Слайд 19
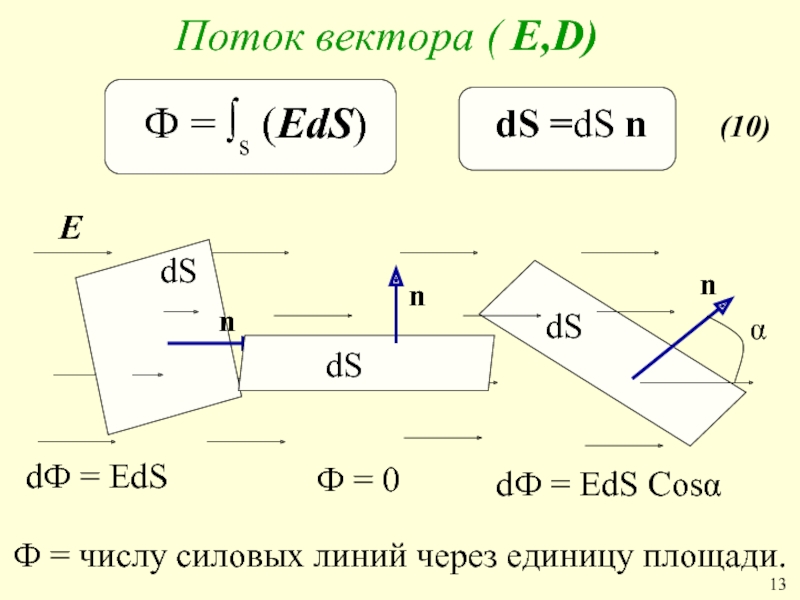
Поток вектора ( Е,D)
Е
n
n
n
α
dФ = ЕdS
Ф = 0
dФ = ЕdS
Ф = числу силовых линий через единицу площади.
Ф = ∫s (ЕdS)
dS
dS
dS
(10)
13
dS =dS n
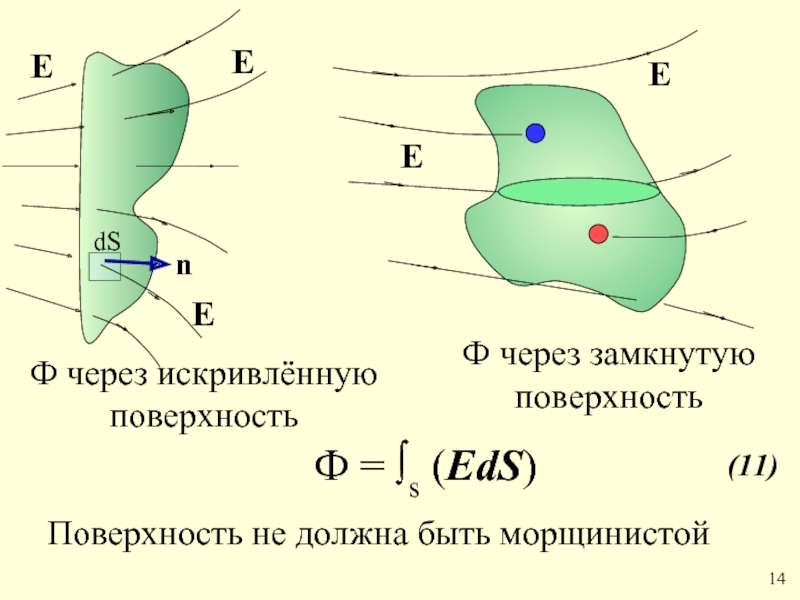
Слайд 20Ф через искривлённую поверхность
Ф = ∫s (ЕdS)
Ф через замкнутую поверхность
Поверхность не
(11)
14
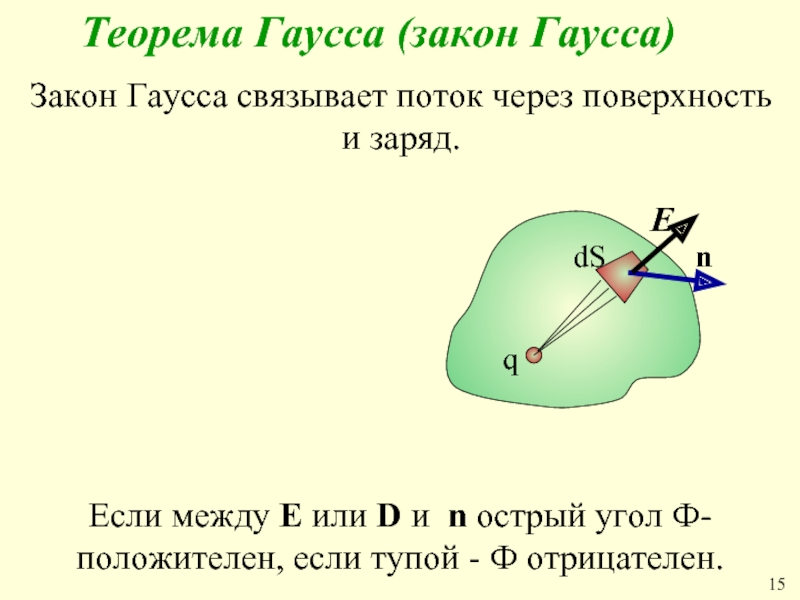
Слайд 21 Теорема Гаусса (закон Гаусса)
Закон Гаусса связывает поток через поверхность и
q
n
dS
Е
Если между Е или D и n острый угол Ф- положителен, если тупой - Ф отрицателен.
15
Слайд 23∫
○
dΩ=4π
Если зарядов в объёме V много, то q = ∑qi
17
(15)
Для
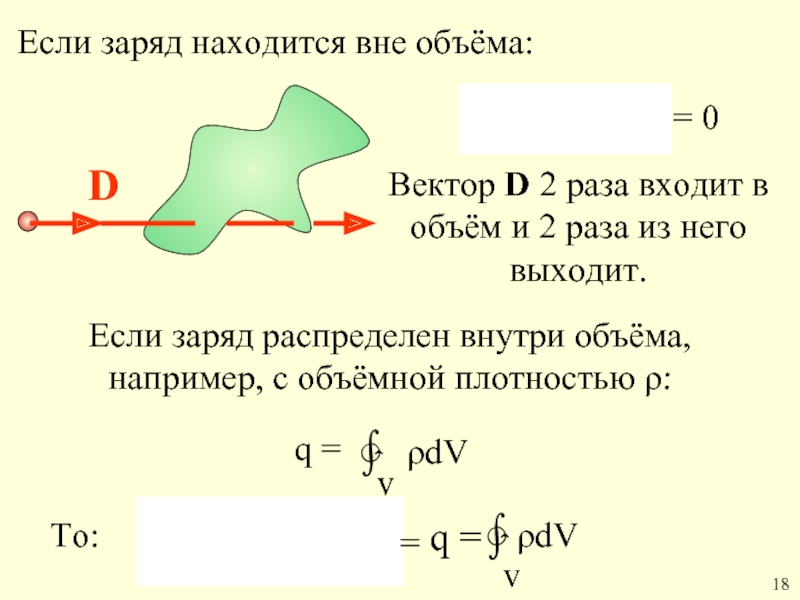
Слайд 24Если заряд находится вне объёма:
D
= 0
Вектор D 2 раза входит
Если заряд распределен внутри объёма, например, с объёмной плотностью ρ:
∳
q =
ρdV
v
∳
q =
ρdV
=
То:
v
18
Слайд 25Физической основой ТОГ является закон Кулона, поэтому теорема Гаусса является интегральной
19
Слайд 26Поток вектора напряженности сквозь произвольную замкнутую поверхность = сумме зарядов, заключённых
Аналогично для потока вектора смещения D
20
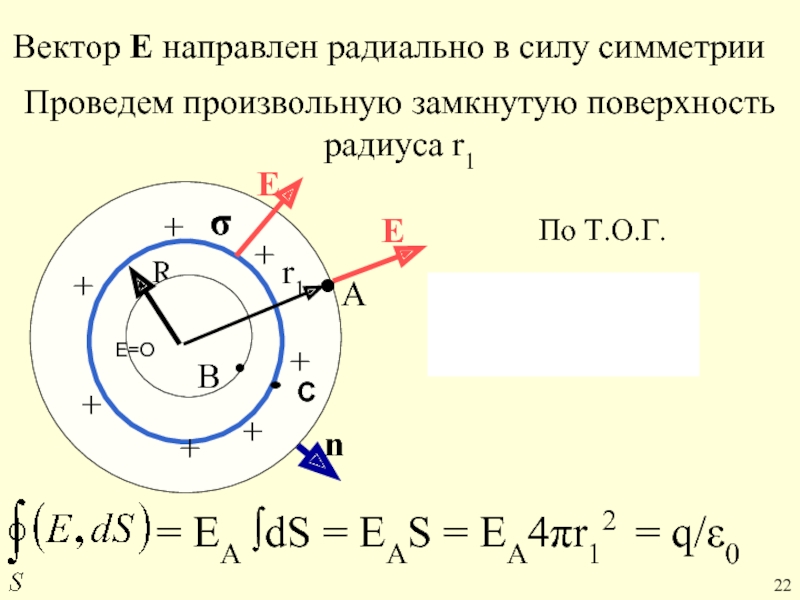
Слайд 27 Применение теоремы Гаусса.
По тонкой сферической оболочке радиуса R равномерно распределён
21
Е
+
R
r1
E
n
+σ
S
А
●
В
●
Слайд 28
Вектор Е направлен радиально в силу симметрии
Проведем произвольную замкнутую поверхность радиуса
= ЕА ∫dS = ЕАS = ЕА4πr12 = q/ε0
22
+
+
+
+
R
r1
+
+
+
σ
Е
n
●
А
По Т.О.Г.
Е
С
●
В
Е=О
Слайд 29
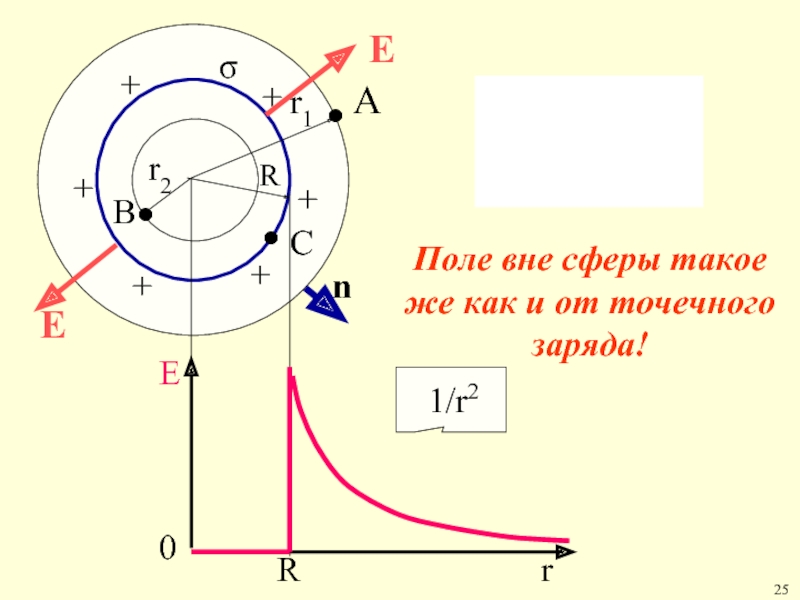
На пов-ти сферы
т.к. S задано q = σSс = σ4πR2
q =
(*)
Из (23)
ЕА вне сферы =
23
Внутри сферы (точка В) Е равно нулю
Слайд 31
Поле Е равномерно заряженной ∞ нити с линейной плотностью τ.
∫(EdS) =
= Е2πаl = q/ε0
q = ∫l τdl
= τl
Окончательно имеем:
= 0
26
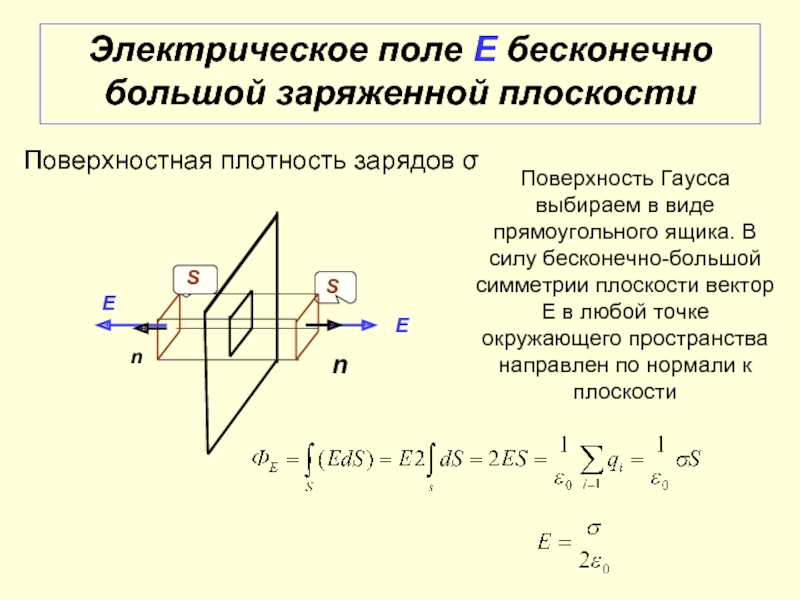
Слайд 32Электрическое поле Е бесконечно большой заряженной плоскости
Поверхностная плотность зарядов σ
Поверхность Гаусса
Е