- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в молекулярную биофизику Лекция № 6 презентация
Содержание
- 1. Введение в молекулярную биофизику Лекция № 6
- 2. План лекции: Температурная денатурация биополимеров.
- 3. Температурная денатурация. Кооперативный характер перехода. ΔG0 =
- 4. Температурная денатурация. Кооперативный характер перехода. При Тпл:
- 5. Конформационная подвижность биополимеров Конформационная подвижность – движение
- 6. Релаксация фрагмента белковой молекулы будет напоминать движение
- 7. Уравнение движения. Определим, какие силы действуют на
- 8. Модель ограниченной диффузии (броуновский осциллятор с сильным
- 9. Модель ограниченной диффузии (броуновский осциллятор с сильным
- 10. Модель ограниченной диффузии (броуновский осциллятор с сильным
- 11. Динамика переходов в биомолекулах. Пример иерархии подходов
- 12. Заключение. Рассмотрены модели образования глобулы, перехода
- 13. Одной из основных функций белков является ферментативная.
- 14. Клеточный рецептор— молекула (обычно белок) на поверхности
- 15. Химическая кинетика. Основные понятия. Скорость реакции (v)
- 16. Химическая кинетика. Основные понятия. Константа равновесия -
- 17. Лиганд-рецепторное взаимодействие. В простейшем случае лиганд (L)
- 18. Кинетика Михаэлиса-Ментен. Этапы: Обратимое образование комплекса фермента
- 19. Кинетика Михаэлиса-Ментен. Константа диссоциации комплекса ES:
- 20. Кинетика Михаэлиса-Ментен. Уравнение Михаэлиса: Это уравнение часто
Слайд 1Введение в молекулярную биофизику
Лекция № 6
Конформационная подвижность
Межмолекулярные взаимодействия
Слайд 2План лекции:
Температурная денатурация биополимеров.
Конформационная подвижность биополимеров физические модели.
Межмолекулярные взаимодействия.
Кинетика Михаэлиса-Ментен.
Введение в молекулярную биофизику
Лекция № 5
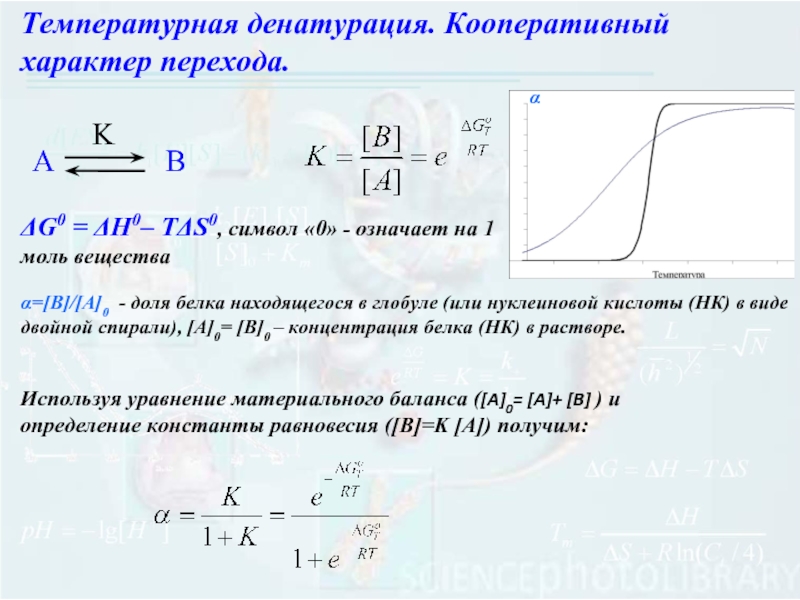
Слайд 3Температурная денатурация. Кооперативный характер перехода.
ΔG0 = ΔH0– TΔS0, символ «0» -
α=[Β]/[Α]0 - доля белка находящегося в глобуле (или нуклеиновой кислоты (НК) в виде двойной спирали), [A]0= [B]0 – концентрация белка (НК) в растворе.
Используя уравнение материального баланса ([A]0= [A]+ [B] ) и определение константы равновесия ([B]=K [A]) получим:
α
Слайд 4Температурная денатурация. Кооперативный характер перехода.
При Тпл: ΔG0 = ΔH0– T·dS0 =
ΔH0 ~ n (количеству звеньев цепи) ΔH10 (энергия разрыва связи одной цепи).
Кооперативный характер означает одновременный переход n звеньев, а его резкость пропорциональна n
α
Тпл
Тпл
Слайд 5Конформационная подвижность биополимеров
Конформационная подвижность – движение групп атомов (отдельных атомов) с
Если длина свободного пробега частицы в плотной среде:
m – масса частицы (~ 100 а.е.м.), γ – коэффициент трения.
Движение фрагмента белка определяется 2-мя потенциалами:
U(x) – конформационный потенциал (изменение потенциальной энергии системы, связанное с изменением конформации)
D(x) - конформационная диффузия (взаимодействие с окружающей средой)
x – обобщенная координата (конформация)
то движение фрагмента биополимера носит диффузионный
или стохастический характер.
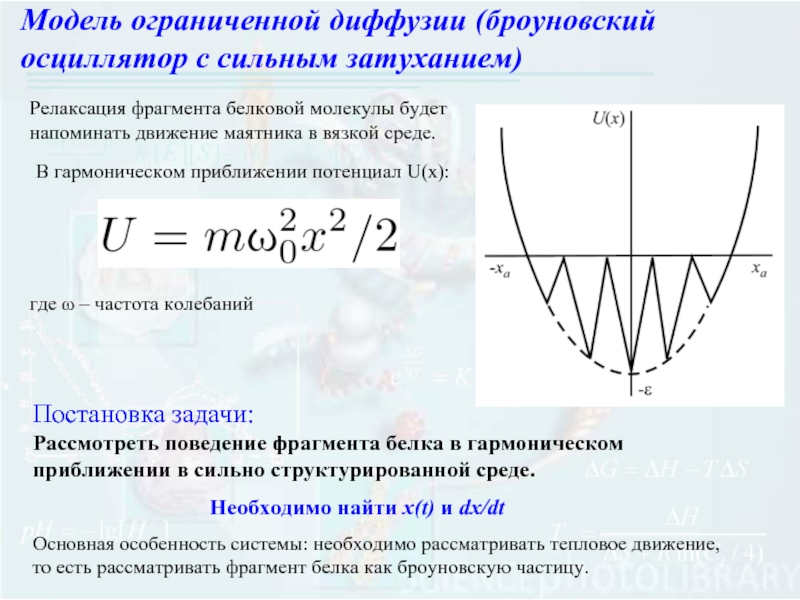
Слайд 6Релаксация фрагмента белковой молекулы будет напоминать движение маятника в вязкой среде.
В
где ω – частота колебаний
Постановка задачи:
Рассмотреть поведение фрагмента белка в гармоническом приближении в сильно структурированной среде.
Основная особенность системы: необходимо рассматривать тепловое движение, то есть рассматривать фрагмент белка как броуновскую частицу.
Модель ограниченной диффузии (броуновский осциллятор с сильным затуханием)
Необходимо найти x(t) и dx/dt
Слайд 7Уравнение движения.
Определим, какие силы действуют на фрагмент молекулы в гармоническом приближении:
Сила
Fупр= dU(x)/dx=-mω02x в гармоническом приближении
2) Сила трения, направленная против скорости движения и пропорциональная ей:
Fтр= -γ(dx/dt),
где γ –коэффициент трения, определяется формулой Стокса: γ=6πbη,
b-характерный размер движущегося участка, η – вязкость среды.
3) Сила, возникающая, в результате теплового движения среды и имеющая случайный характер:
Fст(t)=Σi F(ti), ti – случайные моменты времени.
Уравнение движения (Ланжевена):
Модель ограниченной диффузии (броуновский осциллятор с сильным затуханием)
Слайд 8Модель ограниченной диффузии (броуновский осциллятор с сильным затуханием)
Решение ищется в виде
φ(t) =
x(t) – случайное значение в момент времени t
<> - усреднение по времени
φ(t) – показывает степень статистической независимости величин x(t) и x(t+τ).
φ(t) =
При τ=0: φ(0) =
Так как φ(t) не зависит от t, а зависит от τ, то полагая начальный момент t=0 и изменяя обозначения τ = t, можно записать:
Слайд 9Модель ограниченной диффузии (броуновский осциллятор с сильным затуханием).
Таким образом, получим:
φ(t) =
При больших временах справедливо асимптотическое приближение:
φ(t) ~
где τc – время корреляции стохастического движения, определяющее скорость затухания случайного отклонения от положения равновесия.
Найдем среднеквадратичное отклонение от положения равновесия.
Так как Fст(t) – случайная сила, то Фурье-образ функции корреляции будет иметь вид:
Слайд 10Модель ограниченной диффузии (броуновский осциллятор с сильным затуханием).
Делая обратное преобразование Фурье
1. Для слабозатухающих колебаний при ω0>>γ/(2m)
2. Для ограниченной диффузии при ω0 •• γ/(2μ)
2. Для ограниченной диффузии при ω0 << γ/(2m)
1. Для слабозатухающих колебаний при ω0>>γ/(2m)
Подставляя в выражение для среднеквадратичного отклонения получим:
Слайд 11Динамика переходов в биомолекулах.
Пример иерархии подходов для моделирования биополимеров на примере
Эластичный стержень
2) Два эластичных стержня
3) Учет того, что цепи состоят из сахара, фосфатного остатка и гетероциклического основания
4) Решеточные модели (описывают движение атомов, составляющих решетку)
5) Моделирование на уровне отдельных атомарных взаимодействий
Слайд 12Заключение.
Рассмотрены модели образования глобулы, перехода глобула-клубок и конформационная подвижность биополимеров.
Даже на
Слайд 13Одной из основных функций белков является ферментативная.
Ферменты – катализаторы биохимических реакций.
Катализатор
Межмолекулярные взаимодействия.
Слайд 14Клеточный рецептор— молекула (обычно белок) на поверхности клетки, клеточных органелл или
Вещество, специфически соединяющееся с рецептором, называется лигандом этого рецептора.
Физика ферментов.
Слайд 15Химическая кинетика. Основные понятия.
Скорость реакции (v) – изменение концентрации реагента или
Константа скорости реакции (k) - коэффициент пропорциональности в кинетическом уравнении.
Физический смысл константы скорости реакции k следует из уравнения закона действующих масс: k численно равна скорости реакции при концентрации каждого из реагирующих веществ равной 1 моль/л.
Константа скорости реакции зависит от температуры, от природы реагирующих веществ, но не зависит от их концентрации.
Энергия активации (Е) показывает, какой минимальной энергией должны обладать частицы, чтобы они могли вступить в химическую реакцию.
k0 – предэкспоненциальный множитель
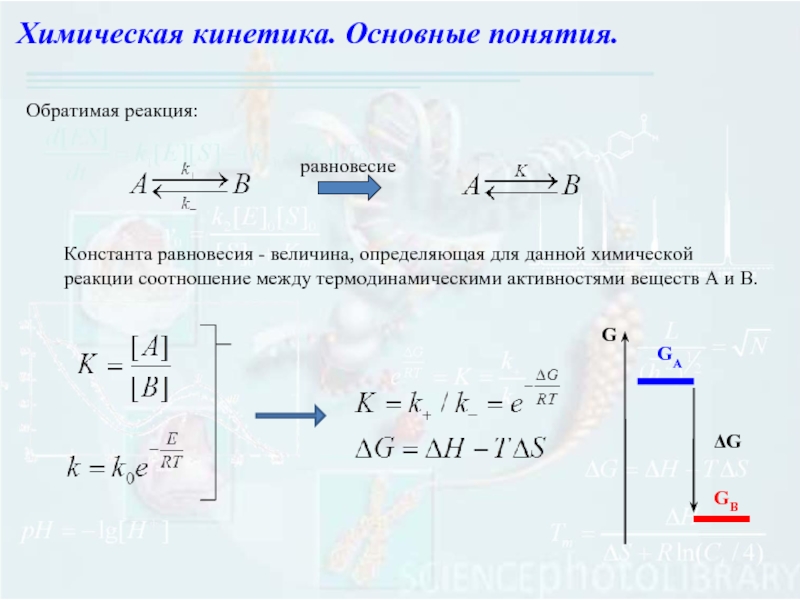
Слайд 16Химическая кинетика. Основные понятия.
Константа равновесия - величина, определяющая для данной химической
равновесие
Обратимая реакция:
GA
GB
G
ΔG
Слайд 17Лиганд-рецепторное взаимодействие.
В простейшем случае лиганд (L) – рецепторное (R) взаимодействие описывается
Закон сохранения вещества для данной системы:
Скорость реакции:
В стационарных условиях (d[LR]/dt=0), где K=k-/k+- константа диссоциации (случай равновесного связывания):
Слайд 18Кинетика Михаэлиса-Ментен.
Этапы:
Обратимое образование комплекса фермента (E) с субстратом (S)
Необратимое превращение субстрата
! Фермент играет роль катализатора.
Кинетическая схема описывается 2-мя кинетическими уравнениями:
и 2-мя уравнениями материально баланса:
Слайд 19Кинетика Михаэлиса-Ментен.
Константа диссоциации комплекса ES:
В случае избытка субстрата ([S]>>[E]0):
В случае квазистационарного
В случае [S]>>[E]0:
Константа Михаэлиса:














![Кинетика Михаэлиса-Ментен.Константа диссоциации комплекса ES:В случае избытка субстрата ([S]>>[E]0):В случае квазистационарного приближения (vES=0):В случае [S]>>[E]0:Константа Михаэлиса:](/img/tmb/1/51509/157a67407c672159a7510b50137d39ba-800x.jpg)