- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КЛАССИФИКАЦИЯ СИГНАЛОВ презентация
Содержание
- 1. КЛАССИФИКАЦИЯ СИГНАЛОВ
- 2. Классификация сигналов Гольфельд Э.И. Случайными или стохастическими или
- 3. Классификация сигналов Гольфельд Э.И. Примеры случайных сигналов:
- 4. Классификация сигналов Гольфельд Э.И. Детерминированными или регулярными называются
- 5. Классификация сигналов Гольфельд Э.И. При помощи детерминированных сигналов
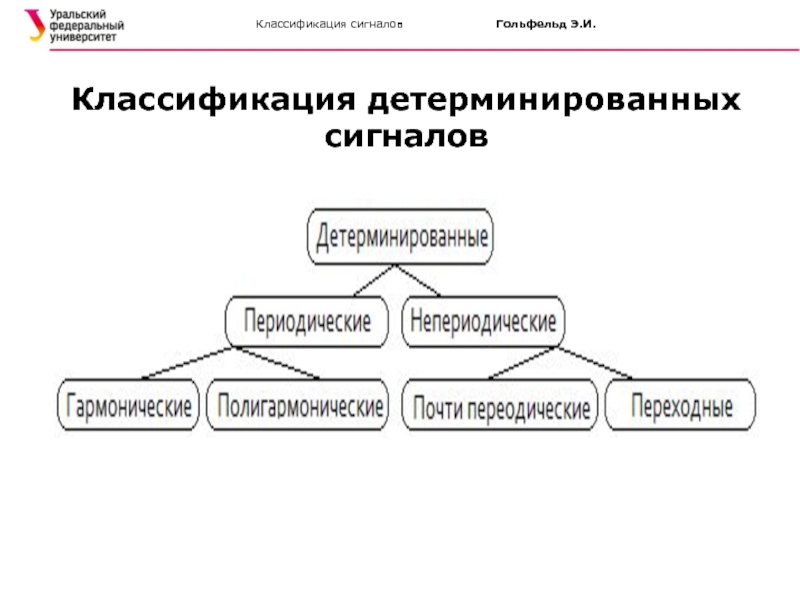
- 6. Классификация сигналов Гольфельд Э.И. Классификация детерминированных сигналов
- 7. Классификация сигналов Гольфельд Э.И. Сигналы, характеризующие периодические явления,
- 8. Классификация сигналов Гольфельд Э.И. Сигналы, характеризующие периодические явления,
- 9. Классификация сигналов Гольфельд Э.И. Непериодический сигнал - частный
- 10. Классификация сигналов Гольфельд Э.И. Одним из наиболее часто
- 11. Классификация сигналов Гольфельд Э.И. Пример гармонического сигнала Пример
- 12. Классификация сигналов Гольфельд Э.И. Полигармонические сигналы составляют наиболее
- 13. Классификация сигналов Гольфельд Э.И. Пример полигармонического сигнала Полигармонический сигнал
- 14. Классификация сигналов Гольфельд Э.И. Чтобы найти Tр нужно
- 15. Классификация сигналов Гольфельд Э.И. Почти периодические сигналы
- 16. Классификация сигналов Гольфельд Э.И. К переходным сигналам относятся
- 17. Классификация сигналов Гольфельд Э.И. К переходным сигналам
- 18. СПАСИБО ЗА ВНИМАНИЕ
Слайд 2Классификация сигналов Гольфельд Э.И.
Случайными или стохастическими или недетерминированными называются такие сигналы, изменение
Такие сигналы описываются случайными функциями.
Случайные сигналы
Случайной функцией некоторой независимой переменной x называют такую функцию y(x), значение которой при любом заданном x является случайной величиной. Случайные функции, для которых независимой переменной является время t, обычно называют случайными (или стохастическими) процессами (сигналами).
Случайность процесса проявляется в том, что вид функции x(t) случайным образом меняется от одного опыта к другому. Функцию, получаемую в результате каждого отдельного опыта, называют реализацией случайного процесса.
Слайд 3Классификация сигналов Гольфельд Э.И.
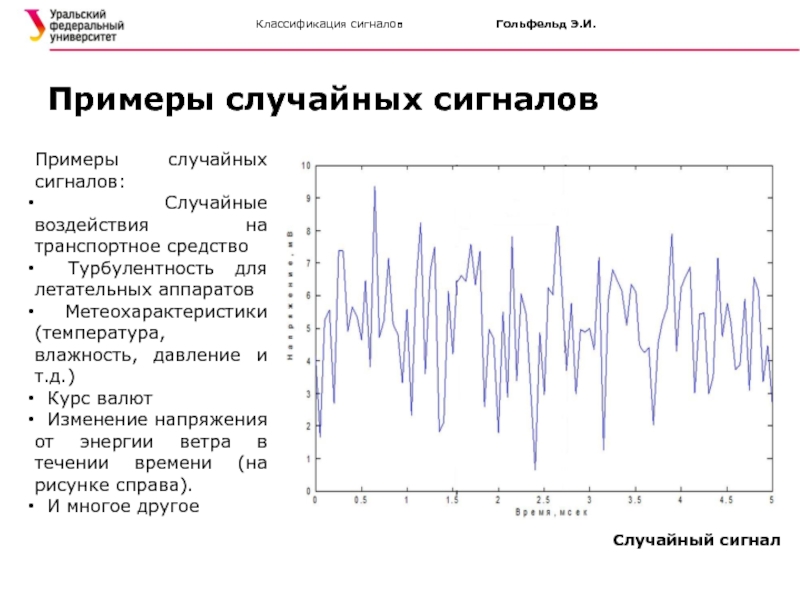
Примеры случайных сигналов:
Случайные воздействия на транспортное средство
Турбулентность
Метеохарактеристики (температура, влажность, давление и т.д.)
Курс валют
Изменение напряжения от энергии ветра в течении времени (на рисунке справа).
И многое другое
Примеры случайных сигналов
Случайный сигнал
Слайд 4Классификация сигналов Гольфельд Э.И.
Детерминированными или регулярными называются такие сигналы, значения которых в
Детерминированные сигналы
Детерминированные сигналы в чистом виде в природе существовать не могут. Такие сигналы могли бы возникнуть только в изолированных системах.
Любая же система находится в некоторой среде, и эта среда влияет на процессы, происходящие в системе. Поэтому детерминированные сигналы являются определенной идеализацией реальных сигналов и не содержат информации.
Слайд 5Классификация сигналов Гольфельд Э.И.
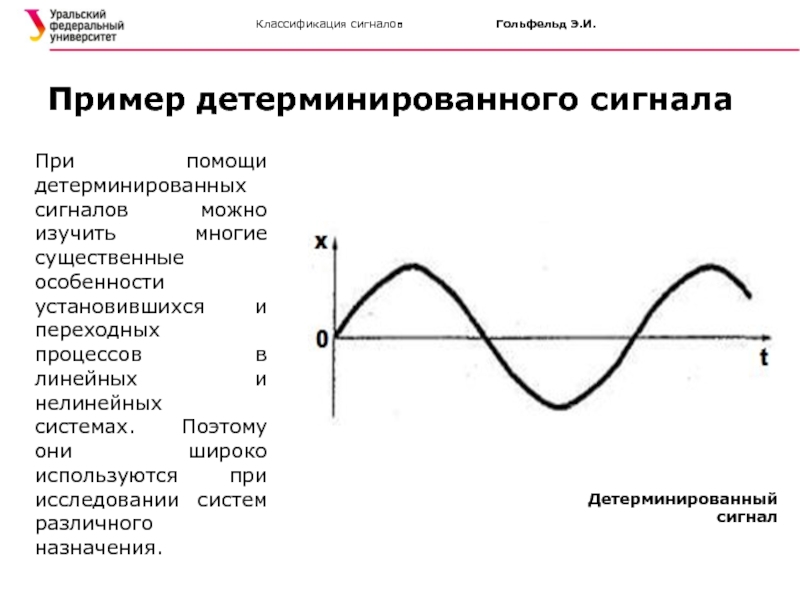
При помощи детерминированных сигналов можно изучить многие существенные особенности
Пример детерминированного сигнала
Детерминированный сигнал
Слайд 7Классификация сигналов Гольфельд Э.И.
Сигналы, характеризующие периодические явления, возвращаются к своим прежним значениям
Основная особенность периодического сигнала состоит в том, что его значения периодически повторяются и что периодичность эта существует вечно.
Периодические сигналы
Детерминированные сигналы в чистом виде в природе существовать не могут. Такие сигналы могли бы возникнуть только в изолированных системах.
Любая же система находится в некоторой среде, и эта среда влияет на процессы, происходящие в системе. Поэтому детерминированные сигналы являются определенной идеализацией реальных сигналов и не содержат информации.
Слайд 8Классификация сигналов Гольфельд Э.И.
Сигналы, характеризующие периодические явления, возвращаются к своим прежним значениям
Основная особенность периодического сигнала состоит в том, что его значения периодически повторяются и что периодичность эта существует вечно.
Периодические сигналы
Примеры периодических сигналов
Слайд 9Классификация сигналов Гольфельд Э.И.
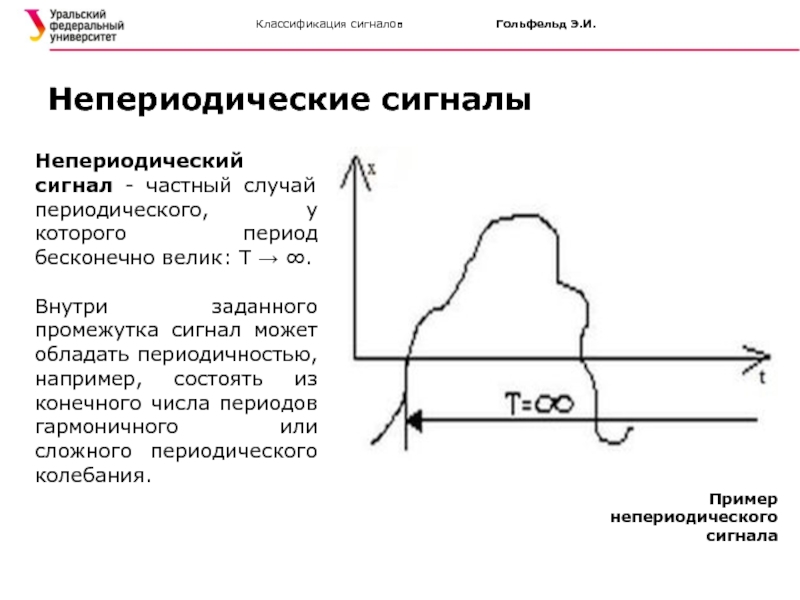
Непериодический сигнал - частный случай периодического, у которого период
Внутри заданного промежутка сигнал может обладать периодичностью, например, состоять из конечного числа периодов гармоничного или сложного периодического колебания.
Непериодические сигналы
Пример непериодического сигнала
Слайд 10Классификация сигналов Гольфельд Э.И.
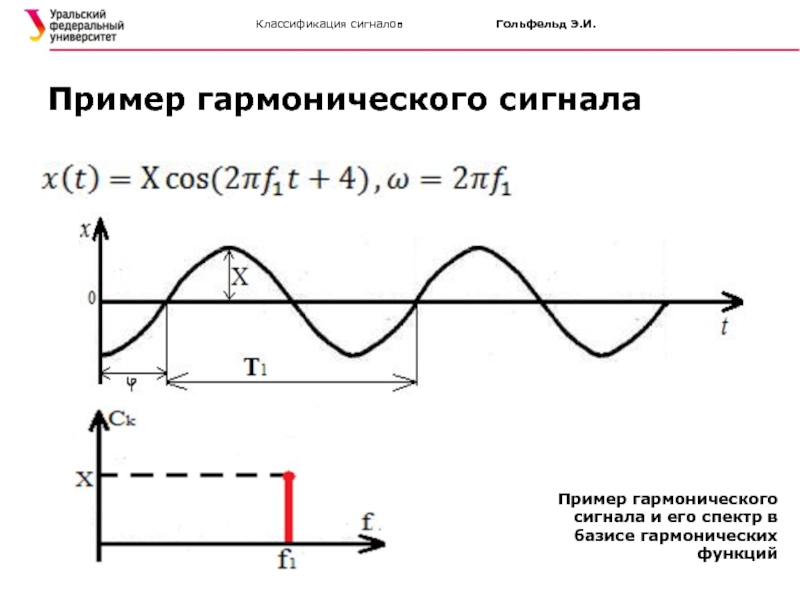
Одним из наиболее часто используемых типов детерминированных периодических сигналов
Гармонические сигналы
Слайд 11Классификация сигналов Гольфельд Э.И.
Пример гармонического сигнала
Пример гармонического сигнала и его спектр в
Слайд 12Классификация сигналов Гольфельд Э.И.
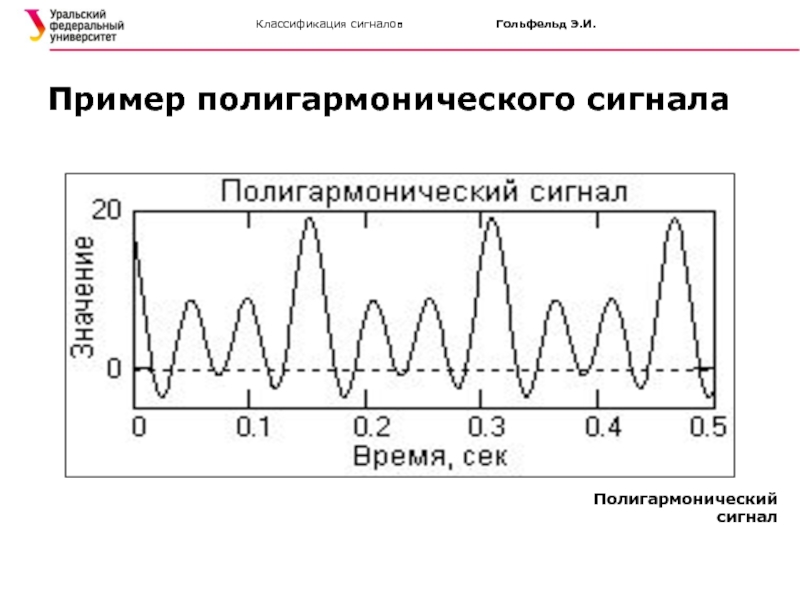
Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов
- основной период
Полигармонический сигнал может быть представлен как:
Полигармонические сигналы
Слайд 13Классификация сигналов Гольфельд Э.И.
Пример полигармонического сигнала
Полигармонический сигнал
Слайд 14Классификация сигналов Гольфельд Э.И.
Чтобы найти Tр нужно найти минимальную частоту, т.е. наименьший
Пример на тему Полигармонические сигналы
Спектр полигармонического сигнала
Слайд 15Классификация сигналов Гольфельд Э.И.
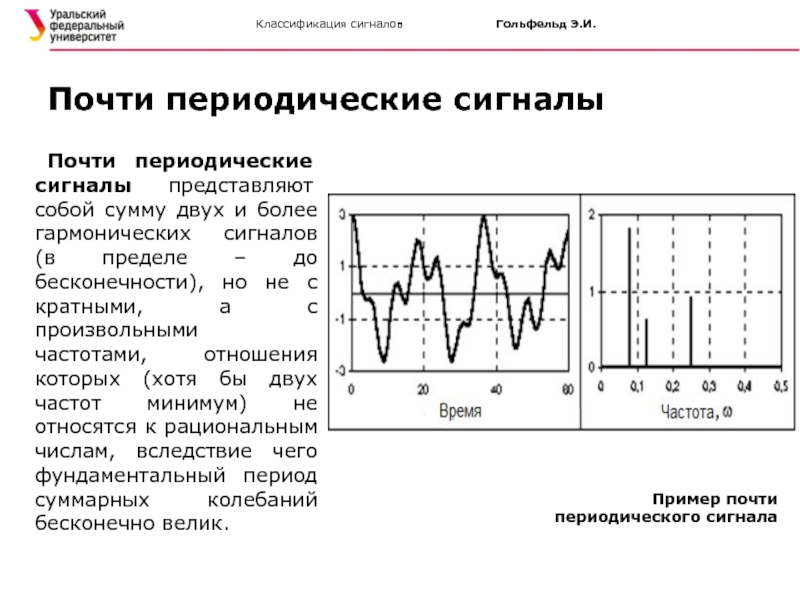
Почти периодические сигналы представляют собой сумму двух и
Почти периодические сигналы
Пример почти периодического сигнала
Слайд 16Классификация сигналов Гольфельд Э.И.
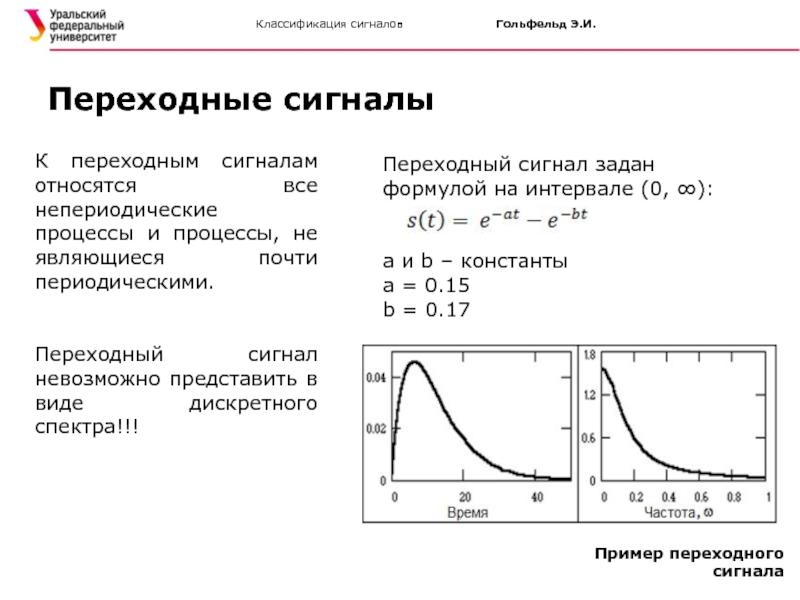
К переходным сигналам относятся все непериодические процессы и процессы,
Переходный сигнал невозможно представить в виде дискретного спектра!!!
Переходные сигналы
Переходный сигнал задан формулой на интервале (0, ∞):
a и b – константы
a = 0.15
b = 0.17
Пример переходного сигнала
Слайд 17Классификация сигналов Гольфельд Э.И.
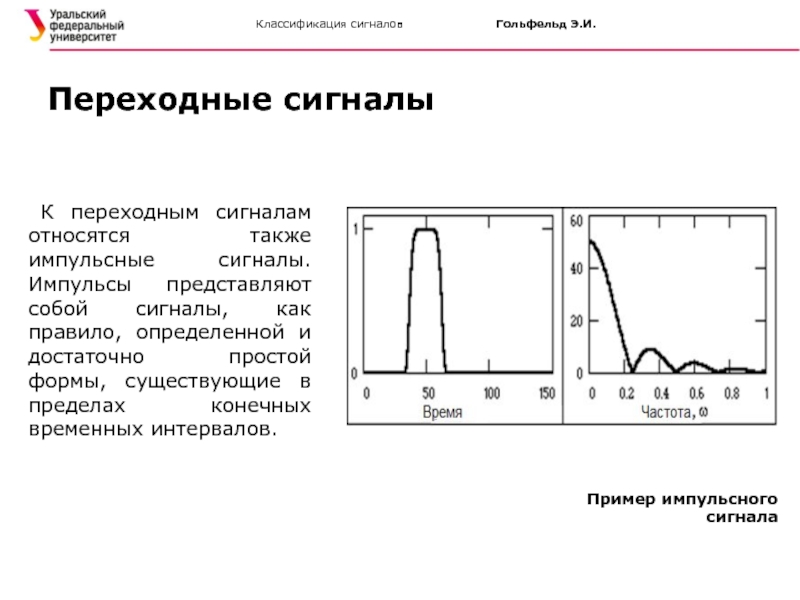
К переходным сигналам относятся также импульсные сигналы. Импульсы
Переходные сигналы
Пример импульсного сигнала