курс
Руководитель: Перепелкин Владислав Александрович
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Зимняя школа 2013 Параллельная реализация построения множества Мандельброта Выполнил: Матвеев Алексей, ФИТ 3 курс Руководитель: Перепелкин Владислав Александрович презентация
Содержание
- 1. Зимняя школа 2013 Параллельная реализация построения множества Мандельброта Выполнил: Матвеев Алексей, ФИТ 3 курс Руководитель: Перепелкин Владислав Александрович
- 2. Множество Мандельброта — это множество таких
- 3. Множество Мандельброта
- 4. Идея решения Для решения было принято распределить
- 5. Реализация Последовательная версия Многопоточная версия (pthread) Версия на множество многопоточных процессов (mpi + pthread)
- 6. Часть множества Мандельброта
- 7. Тестирование В ходе тестирования был подтвержден тот
- 8. Результаты Были реализованы три версии программы (последовательная,
Слайд 1Зимняя школа 2013
Параллельная реализация построения множества Мандельброта
Выполнил: Матвеев Алексей, ФИТ 3
Слайд 2
Множество Мандельброта — это множество таких точек c на комплексной плоскости,
для которых итеративная последовательность z0=0, zn=zn-12+c (n=1, 2, 3, …) не уходит на бесконечность.
Слайд 4Идея решения
Для решения было принято распределить части комплексной плоскости (полосы вдоль
одной оси) между различными потоками(процессами), и в дальнейшем произвести вычисления элементов последовательности для каждой точки.
Слайд 5Реализация
Последовательная версия
Многопоточная версия (pthread)
Версия на множество многопоточных процессов (mpi + pthread)
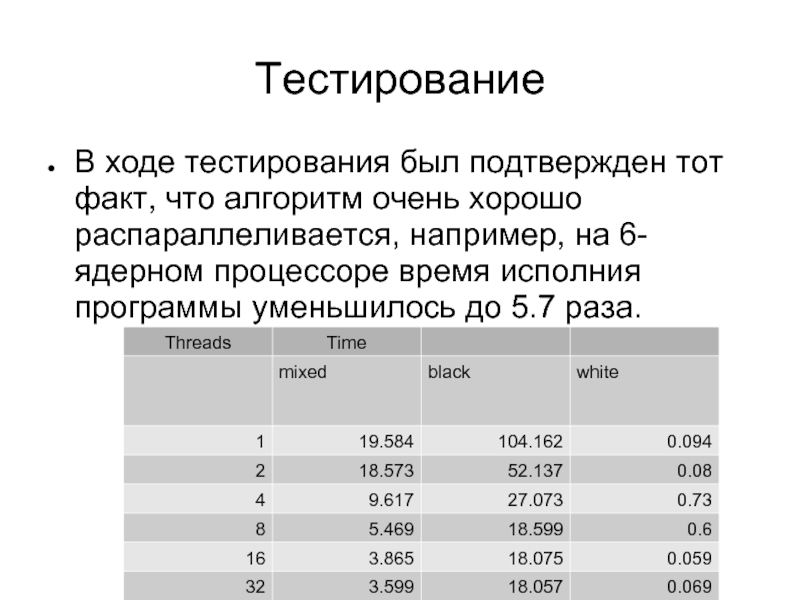
Слайд 7Тестирование
В ходе тестирования был подтвержден тот факт, что алгоритм очень хорошо
распараллеливается, например, на 6-ядерном процессоре время исполния программы уменьшилось до 5.7 раза.
Слайд 8Результаты
Были реализованы три версии программы (последовательная, pthread, mpi+pthread) и протестированы возможности
распараллеливания версии на pthread, в дальнейшем будет произведено тестирование версии mpi+pthread.