- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаємне розташування прямих на площині презентация
Содержание
- 1. Взаємне розташування прямих на площині
- 2. Взаємне розташування прямих
- 3. Аксіоми, означення, теореми Аксіоми геометрії – це
- 4. Суміжні кути Два кути називаються суміжними, якщо
- 5. Вертикальні кути Два кути називаються вертикальними, якщо
- 6. Бліц -турнір Чи вірне твердження: Сума
- 7. Задачі по темі “Вертикальні і суміжні кути”
- 8. Творча задача Від вертикального чоловічка Визначте на
- 9. Перпендикулярні прямі Дві прямі називають перпендикулярними, якщо
- 10. Паралельні прямі Дві прямі на площині називають
- 11. Основна властивість паралельних прямих
- 12. Завдання по темі “Перпендикулярні і паралельні прямі”
- 13. Завдання по темі “Паралельні і перпендикулярні прямі”
- 14. По одну сторону дороги
- 15. Кути, утворені при перетині двох прямих
- 16. Ознаки паралельності прямих Теорема 5: Якщо при
- 17. Завдання по темі: “Ознаки паралельності прямих”
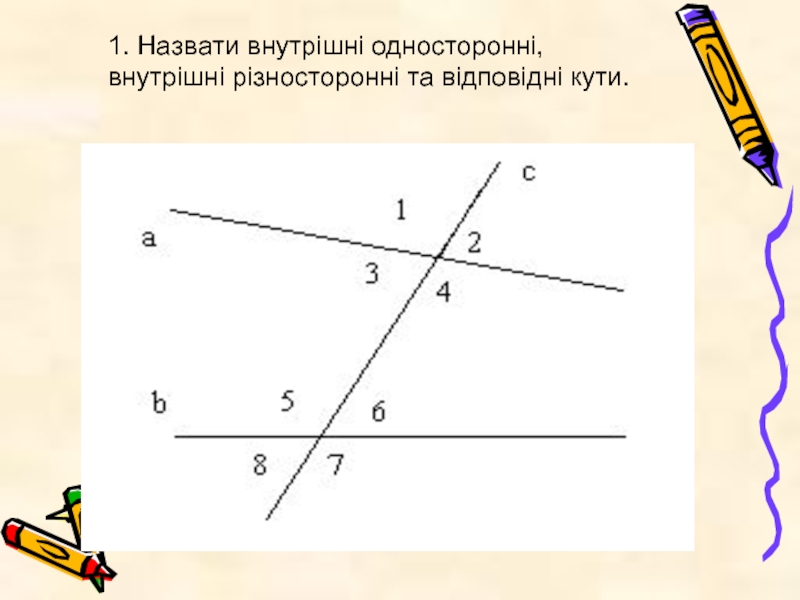
- 18. 1. Назвати внутрішні односторонні, внутрішні різносторонні та відповідні кути.
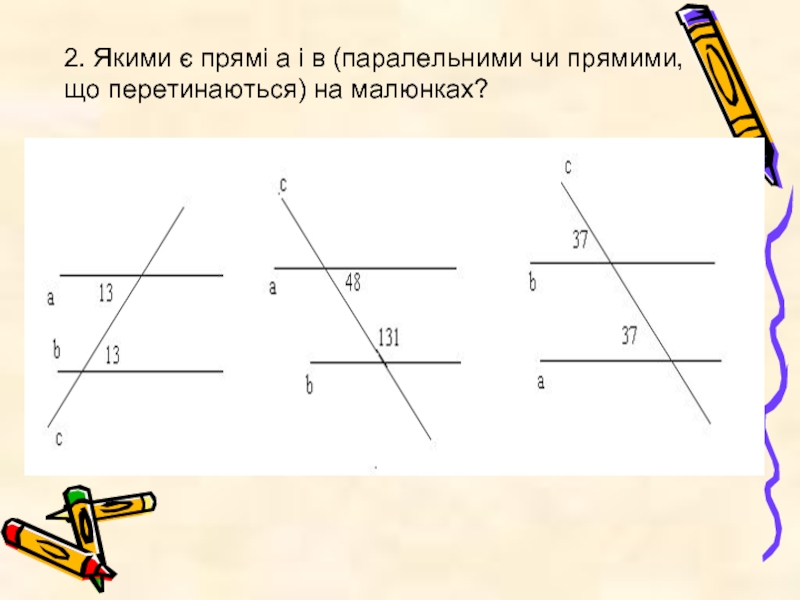
- 19. 2. Якими є прямі а і в (паралельними чи прямими, що перетинаються) на малюнках?
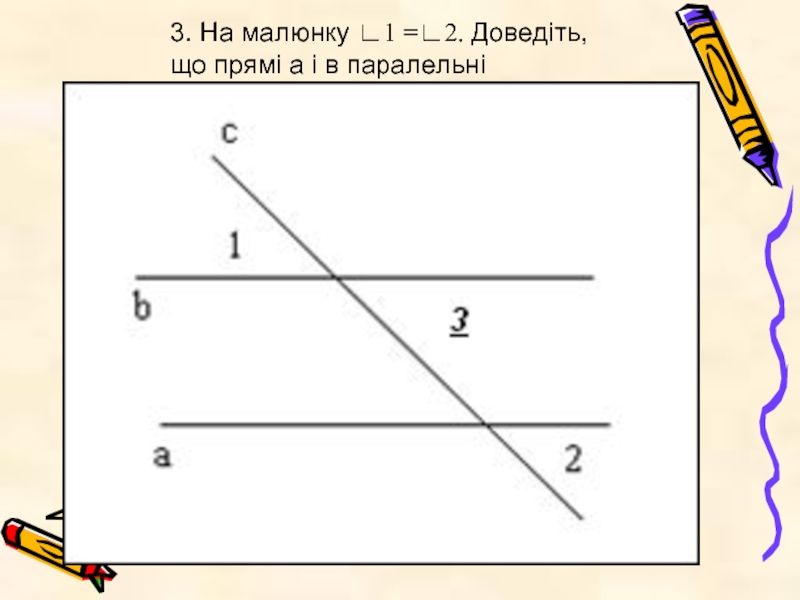
- 20. 3. На малюнку ∟1 =∟2. Доведіть, що прямі а і в паралельні
- 21. 4. На малюнку: MF – бісектриса кута
- 22. Творча задача На плані
- 23. Властивість паралельних прямих Наслідок 2 Відповідні кути,
- 24. Завдання по темі “Властивості паралельних прямих”
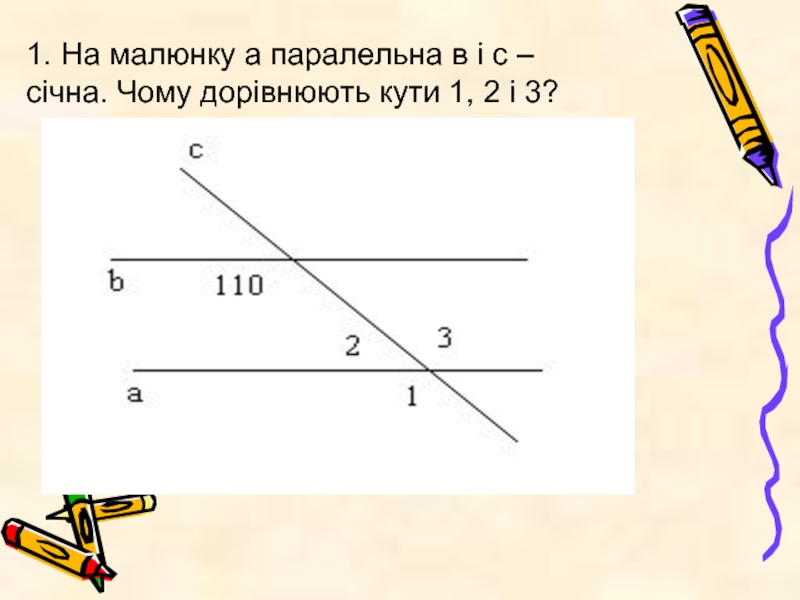
- 25. 1. На малюнку а паралельна в і
- 26. 2.Градусна міра одного з кутів,
- 27. 4. На малюнку кут 1 дорівнює
- 28. Перевір себе: 1. Яким (гострим, тупим чи
- 29. Бажаємо успіхів у подальшому вивченні геометрії !!!
Слайд 2 Взаємне розташування прямих
Мета: Узагальнити і систематизувати теоретичні знання з теми; закріпити вміння та навички використання теоретичних знань до розв‘язування задач.
Розвивати творчий підхід та інтерес до навчання.
Формувати вміння самостійно орієнтуватися в інформаційному просторі.
Виховувати в учнів уміння працювати в групі; відповідальність за себе і за своїх товаришів
Обладнання: ПК, презентації, дидактичний матеріал.
Тип уроку: Урок узагальнення і систематизації знань.
Девіз уроку: “Зібратися разом-це початок, триматися разом-це прогрес; працювати разом-це успіх!”
Генрі Форд
Слайд 3Аксіоми, означення, теореми
Аксіоми геометрії – це твердження про основні властивості найпростіших
У перекладі з грецької слово “аксіома” означає “прийняте положення”.
Твердження, в якому пояснюється зміст того чи іншого поняття (назва), називається означенням.
Математичне твердження, справедливість якого встановлюється за допомогою міркувань, називають теоремою. Саме міркування називають доведенням теореми. Кожна теорема містить умову (те, що дано) і висновок (те, що необхідно довести)
Слайд 4Суміжні кути
Два кути називаються суміжними, якщо одна сторона у них спільна,
Кути АОС і СОВ – суміжні.
Властивість суміжних кутів:
Теорема: Сума мір двох суміжних кутів дорівнює 180º.
Наслідок 1. Кут, суміжний з прямим кутом, - прямий.
Наслідок 2. Кут, суміжний з гострим кутом, - тупий, а суміжний з тупим кутом, - гострий.
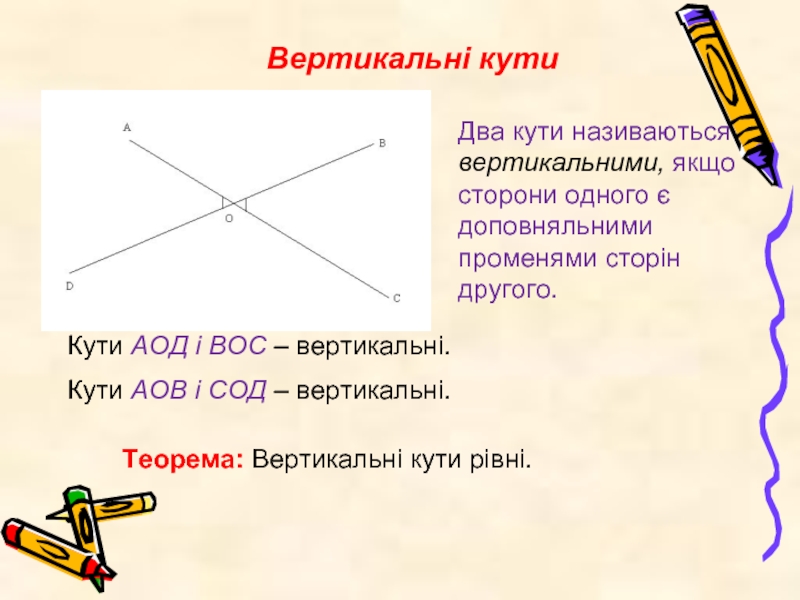
Слайд 5Вертикальні кути
Два кути називаються вертикальними, якщо сторони одного є доповняльними променями
Кути АОД і ВОС – вертикальні.
Кути АОВ і СОД – вертикальні.
Теорема: Вертикальні кути рівні.
Слайд 6Бліц -турнір
Чи вірне твердження:
Сума суміжних кутів 180°?
Сума вертикальних кутів 180°?
Вертикальні
Якщо кути рівні, то вони вертикальні?
Суміжний кут з гострим є гострий кут?
Вертикальний кут до гострого є кут тупий?
Слайд 7Задачі по темі “Вертикальні і суміжні кути”
1. При перетині двох прямих
А.5º і 175º;
Б.15ºі 19º;
В.27ºі 154º;
Г.3ºі 3º.
2. Сума двох кутів, що утворилися при перетині двох прямих 142º. Знайти всі кути, що утворилися.
3. Знайти кут між прямими, що перетинаються, якщо сума трьох з утворених кутів 293º.
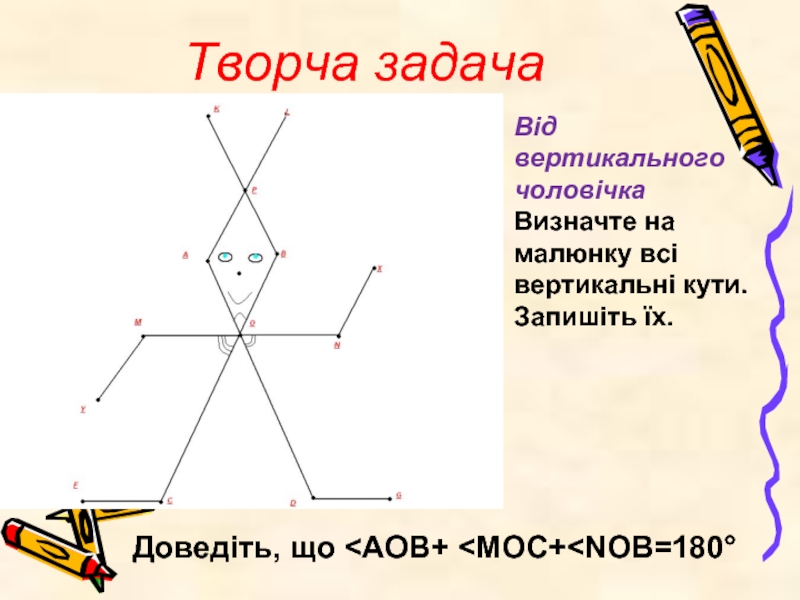
Слайд 8Творча задача
Від вертикального чоловічка
Визначте на малюнку всі вертикальні кути. Запишіть їх.
Доведіть, що <АОВ+ <МОС+
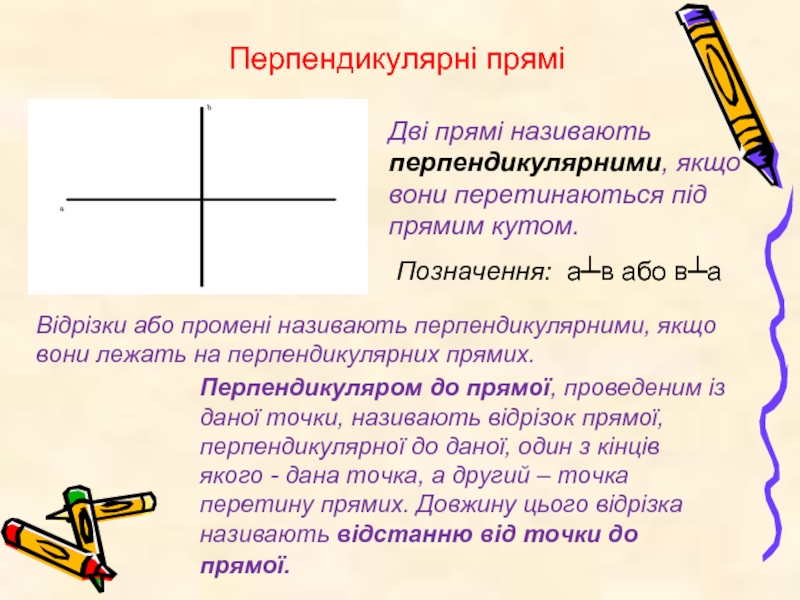
Слайд 9Перпендикулярні прямі
Дві прямі називають перпендикулярними, якщо вони перетинаються під прямим кутом.
Відрізки або промені називають перпендикулярними, якщо вони лежать на перпендикулярних прямих.
Перпендикуляром до прямої, проведеним із даної точки, називають відрізок прямої, перпендикулярної до даної, один з кінців якого - дана точка, а другий – точка перетину прямих. Довжину цього відрізка називають відстанню від точки до прямої.
Слайд 10Паралельні прямі
Дві прямі на площині називають паралельними, якщо вони не перетинаються.
Позначення:
а||в
Два відрізки або промені називають паралельними, якщо вони лежать на паралельних прямих.
Слайд 11Основна властивість
паралельних прямих
Через точку, яка
(аксіома Евкліда)
Давньогрецький геометр Евклід це твердження прийняв без доведення. Його назвали аксіомою Евкліда, тому що всі твердження, які приймають без доведення, називають аксіомами.
Слайд 12Завдання по темі “Перпендикулярні і паралельні прямі”
Бліц -опитування
Чи вірне твердження:
Дві прямі,які
Два відрізки які не перетинаються,параленьні?
Чи прямі АВ і КА паралельні?
Якщо прямі перетинаються і утворюють кут 80º,то вони перпендикулярні?
Якщо дві прямі перпендикулярні до третьої,то ці прямі паралельні?
Слайд 13Завдання по темі “Паралельні і перпендикулярні прямі”
1. Накреслити промені MN і
2. Прямі а і в паралельні. Пряма с не перетинає пряму а. Доведіть, що пряма с не перетинає і пряму в.
Слайд 14
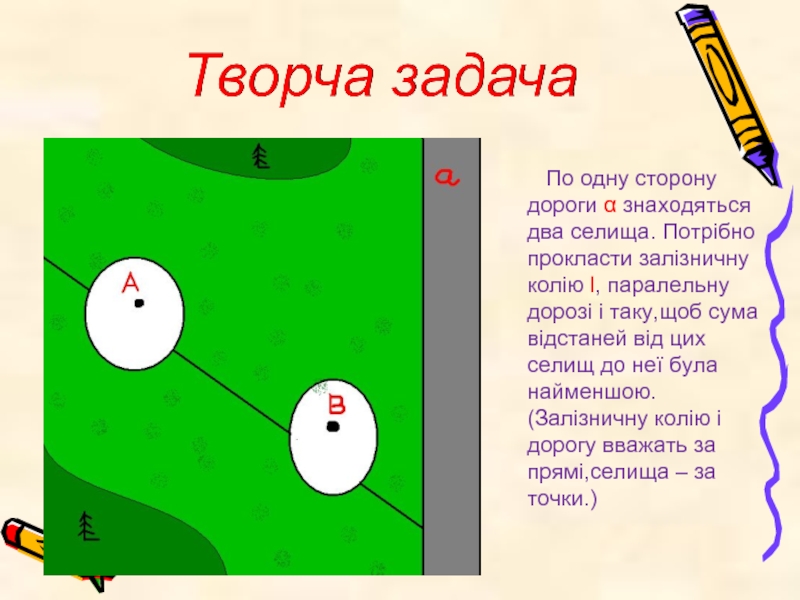
По одну сторону дороги α знаходяться два селища. Потрібно
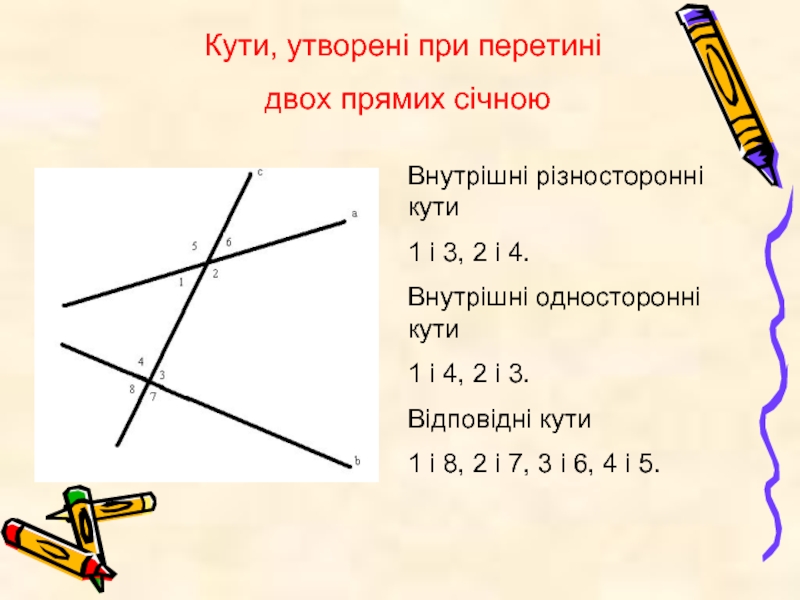
Слайд 15Кути, утворені при перетині
двох прямих січною
Внутрішні різносторонні кути
1 і 3,
Внутрішні односторонні кути
1 і 4, 2 і 3.
Відповідні кути
1 і 8, 2 і 7, 3 і 6, 4 і 5.
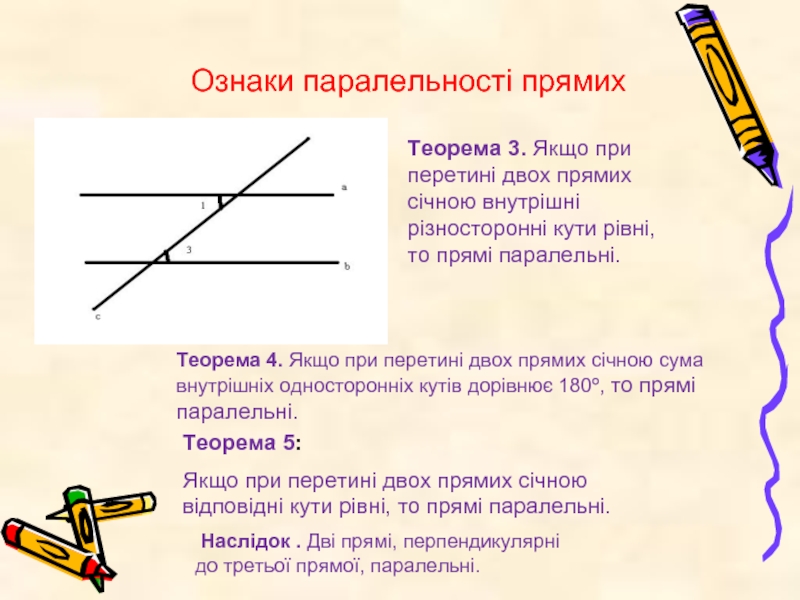
Слайд 16Ознаки паралельності прямих
Теорема 5:
Якщо при перетині двох прямих січною відповідні кути
Теорема 4. Якщо при перетині двох прямих січною сума внутрішніх односторонніх кутів дорівнює 180º, то прямі паралельні.
Теорема 3. Якщо при перетині двох прямих січною внутрішні різносторонні кути рівні, то прямі паралельні.
Наслідок . Дві прямі, перпендикулярні до третьої прямої, паралельні.
Слайд 214. На малюнку: MF – бісектриса кута KMN, KF – бісектриса
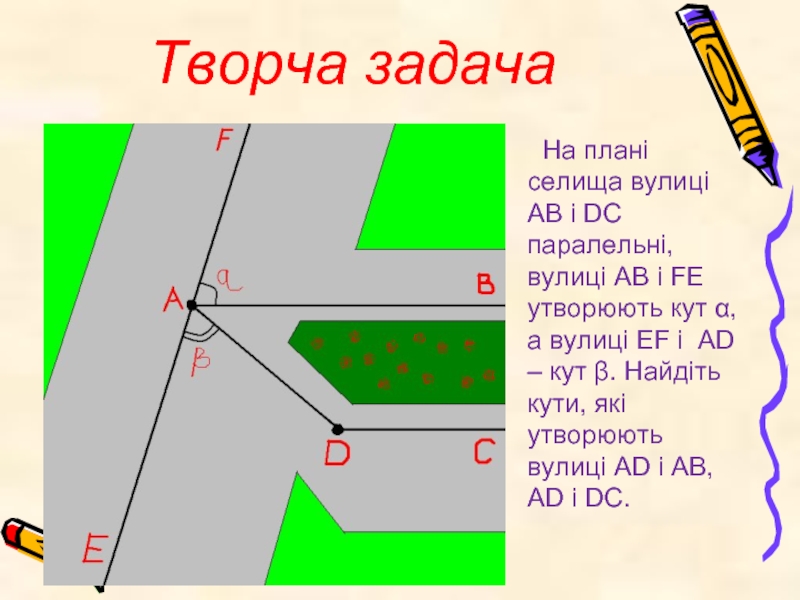
Слайд 22 Творча задача
На плані селища вулиці АВ і DC
Слайд 23Властивість паралельних прямих
Наслідок 2 Відповідні кути, утворені при перетині паралельних прямих
Наслідок 1. Сума внутрішніх односторонніх кутів, утворених при перетині паралельних прямих січною, дорівнює 180º.
Теорема 7. Дві прямі, паралельні третій, паралельні одна одній.
Теорема 6. Внутрішні різносторонні кути, утворені при перетині паралельних прямих січною, рівні.
Слайд 26
2.Градусна міра одного з кутів, що утворилися при перетині січною
3. Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 37 градусів. Чи може один з решти семи кутів дорівнювати:
А) 133, Б)143, В)153.
Слайд 27
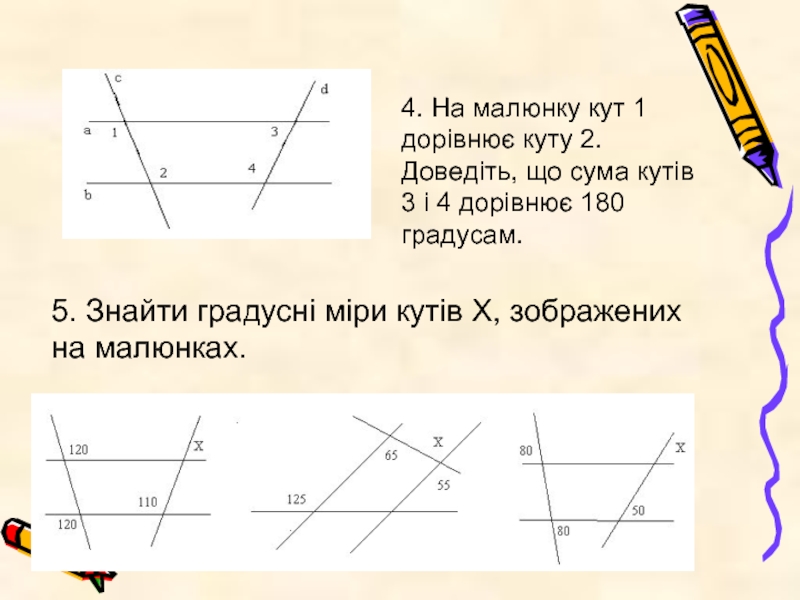
4. На малюнку кут 1 дорівнює куту 2. Доведіть, що сума
5. Знайти градусні міри кутів Х, зображених на малюнках.
Слайд 28Перевір себе:
1. Яким (гострим, тупим чи прямим) є кут, суміжний із
2. Скільки пар суміжних кутів утвориться при перетині двох прямих?
3. Знайдіть кут, суміжний із кутом, що утворюють стрілки годинника, які показують третю годину.
4. Чи є правильним твердження, що для кожного кута можна побудувати тільки один суміжний із ним кут?
5. Чому дорівнює кут між бісектрисами двох вертикальних кутів?
6. Чи можуть вертикальні кути дорівнювати 21 і 39 градусів?
7. Скільки пар вертикальних кутів утвориться при перетині двох прямих?