- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многоугольники получающиеся в сечении куба презентация
Содержание
- 1. Многоугольники получающиеся в сечении куба
- 2. Цель работы: Продемонстрировать плоские многоугольники, которые
- 3. Доказать, что если в сечение куба получится треугольник, то этот треугольник остроугольный. Задача №1
- 4. Построить сечение куба плоскостью, проходящей через
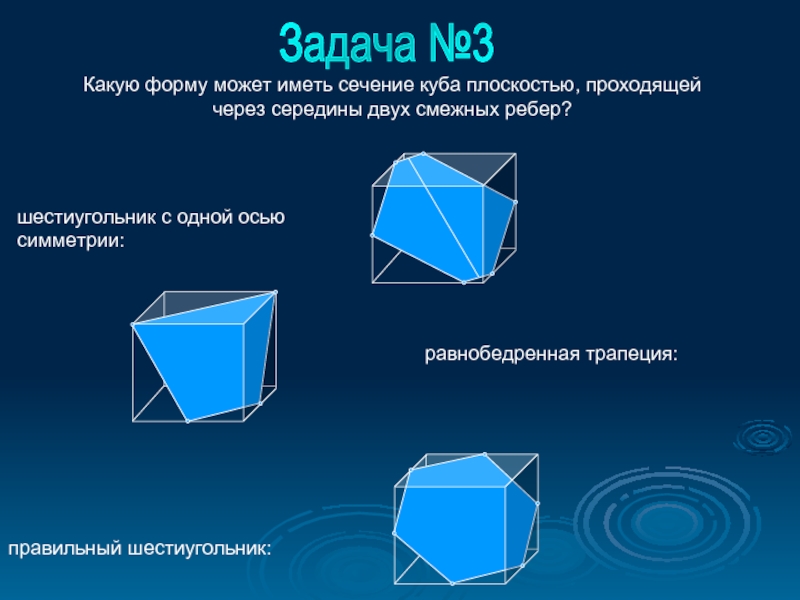
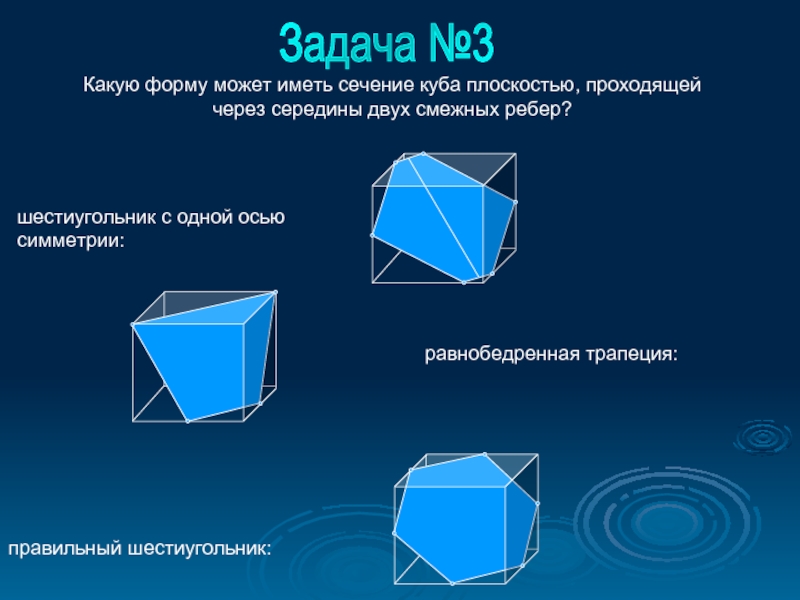
- 5. шестиугольник с одной осью симметрии: правильный шестиугольник:
- 6. Прямоугольник Диагональ куба выбрана в той диагональной
- 7. Трапеция
- 8. Пятиугольник с одной осью Плоскость параллельна
- 9. Правильный шестиугольник
- 10. Треугольник Плоскость параллельна диагонали B’D. Пусть точка
- 11. шестиугольник с одной осью симметрии: правильный шестиугольник:
- 12. Задача №4 равнобедренный треугольник: прямоугольник: пятиугольник с
Слайд 2Цель работы:
Продемонстрировать плоские многоугольники,
которые получаются при сечение
куба плоскостью,
выяснить
Слайд 3
Доказать, что если в сечение куба получится треугольник, то этот треугольник
Задача №1
Слайд 4
Построить сечение куба плоскостью, проходящей через концы трех ребер куба, выходящих
Задача №2
Слайд 5шестиугольник с одной осью симметрии:
правильный шестиугольник:
Задача №3
равнобедренная трапеция:
Какую форму может иметь
Слайд 6Прямоугольник
Диагональ куба выбрана в той диагональной плоскости, которая параллельна прямой МN.
По
Слайд 8Пятиугольник с одной осью
Плоскость параллельна диагонали куба, выходящей из общей
Пусть M и N – середины двух смежных сторон грани A’B’C’D’. Отрезки MN и B’D’ пересекаются в точке Р. Проводим отрезок РК параллельно диагоналям BD’. Через две пересекающиеся прямые PK и MN проводим плоскость KLMNT. Она параллельна диагонали BD’.
Слайд 10Треугольник
Плоскость параллельна диагонали B’D.
Пусть точка Р – пересечение отрезков B’D’ и
Слайд 11шестиугольник с одной осью симметрии:
правильный шестиугольник:
Задача №3
равнобедренная трапеция:
Какую форму может иметь
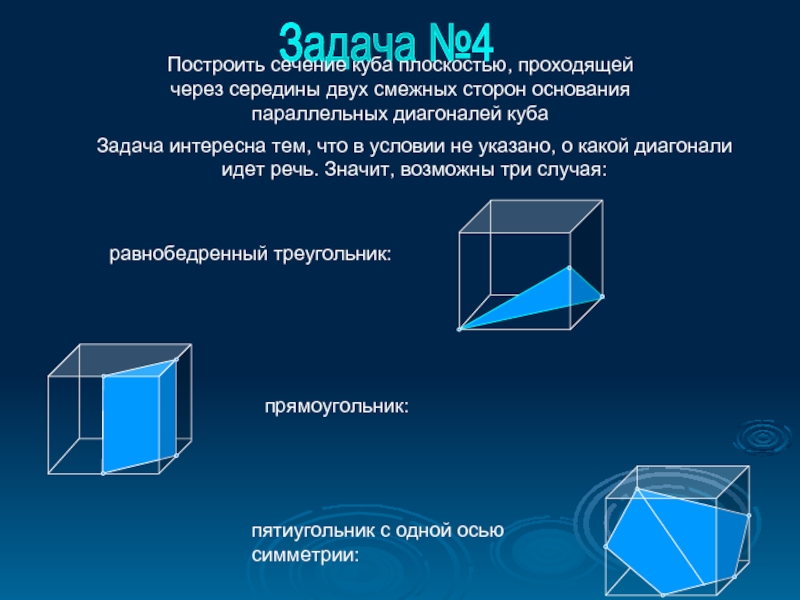
Слайд 12Задача №4
равнобедренный треугольник:
прямоугольник:
пятиугольник с одной осью симметрии:
Построить сечение куба плоскостью, проходящей
Задача интересна тем, что в условии не указано, о какой диагонали идет речь. Значит, возможны три случая: