- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расстояние в пространстве презентация
Содержание
- 1. Расстояние в пространстве
- 2. ХОД УРОКА 1.Проверка домашней работы 2. «Мой
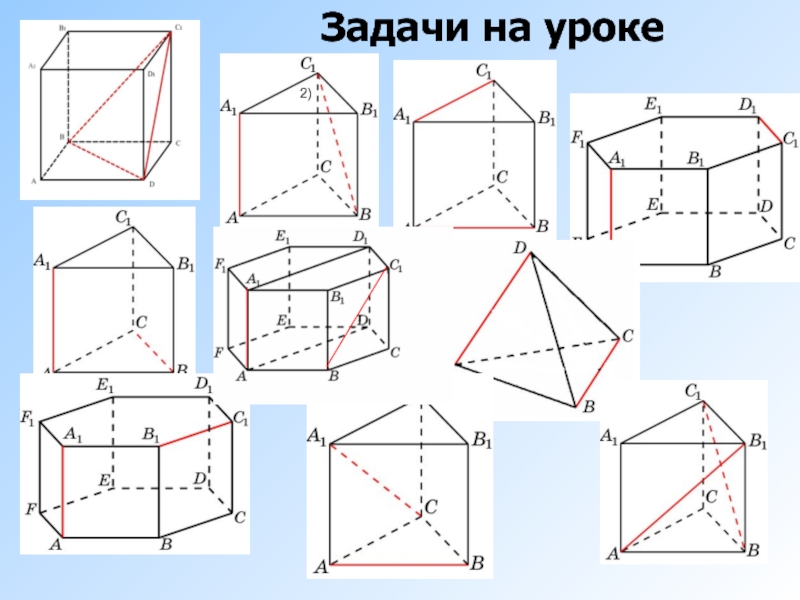
- 3. ) 2) Задачи на уроке
- 4. Расстояние от точки до плоскости
- 6. Второй способ решения задачи:
- 8. РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ Расстоянием между
- 9. Если ортогональная проекция на плоскость переводит прямую
- 10. В правильной треугольной призме ABCA1B1C1, все ребра
- 11. В правильной треугольной призме ABCA1B1C1, все ребра
- 12. В правильной треугольной призме АВСА1В1С1 все ребра
- 13. 4) AA1 · HH1 = 0 a
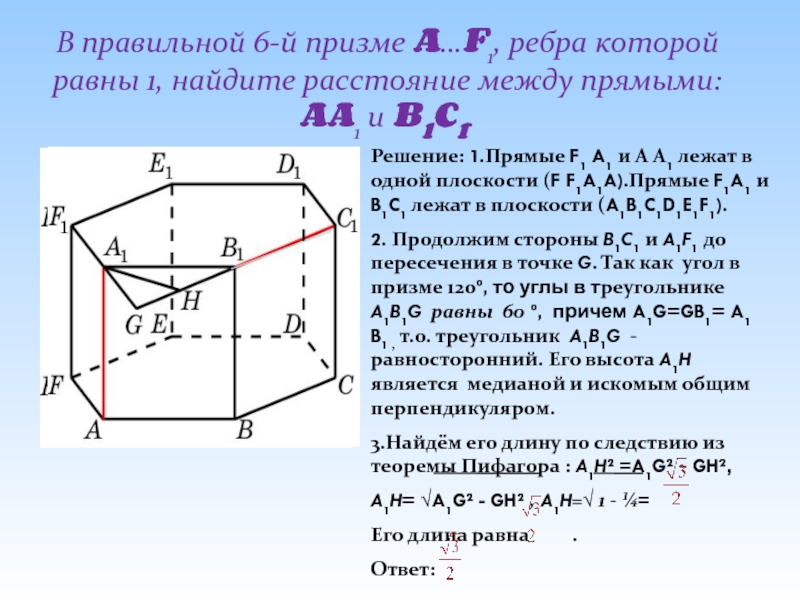
- 14. В правильной 6-й призме A…F1, ребра которой
- 15. В правильной 6-й призме A…F1, ребра которой
- 16. В правильной 6-й призме A…F1, ребра которой
- 17. Ответ: Решение. Искомое расстояние равно длине
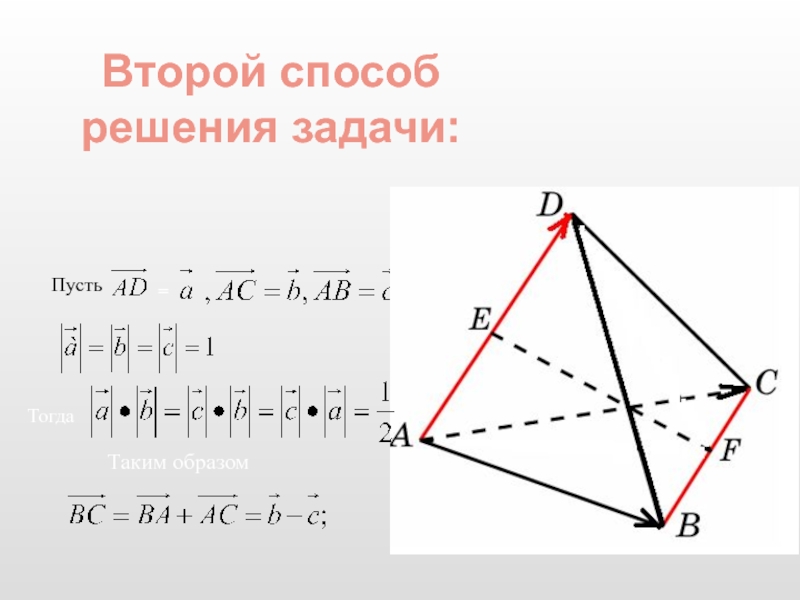
- 18. Второй способ решения задачи: Пусть = Тогда Таким образом
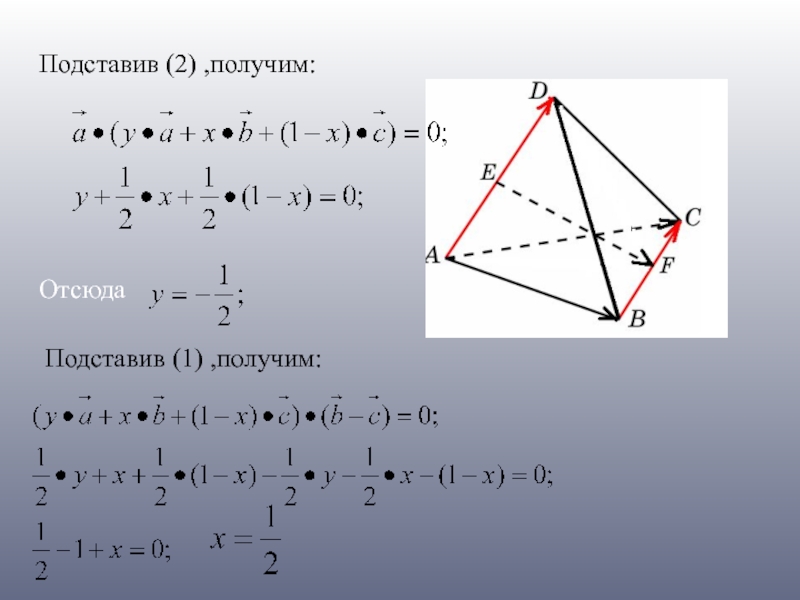
- 19. (1) (2)
- 20. Подставив (2) ,получим: Отсюда Подставив (1) ,получим:
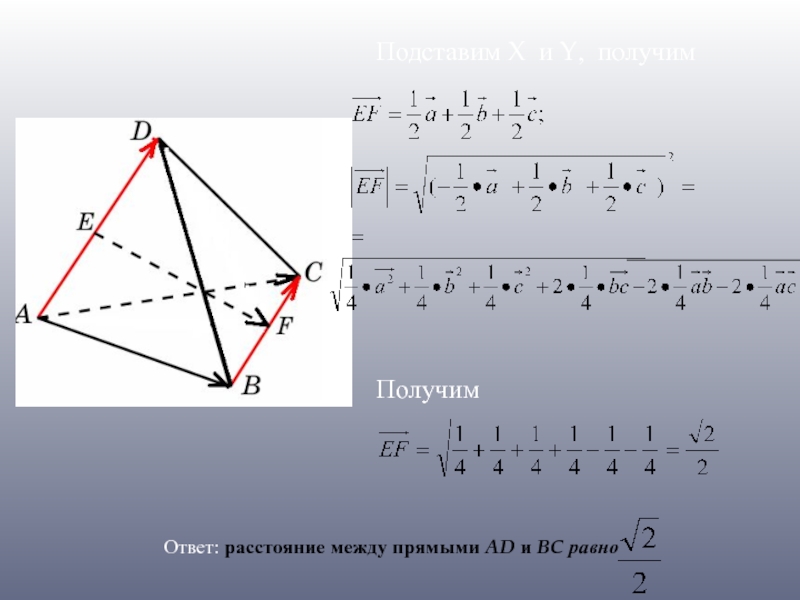
- 21. Подставим X и Y, получим Получим Ответ:
- 22. В правильной треугольной
- 23. 2
- 24. 1) В единичном кубе
- 25. 3) В правильной 6-й призме
- 26. Основанием прямой призмы является
- 27. Расстояние между скрещивающимися прямыми. ABCA’B’C’ – прямоугольная
- 28. M N 1 1
- 29. M N
- 30. M N K
- 31. Домашнее задание В правильной
Слайд 2ХОД УРОКА
1.Проверка домашней работы
2. «Мой маленький проект»
3.Самостоятельная работа
4.Задача из ЕГЭ, уровня
Слайд 8РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ
В ПРОСТРАНСТВЕ
Расстоянием между двумя непересекающимися прямыми в пространстве называется
Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью.
A
B
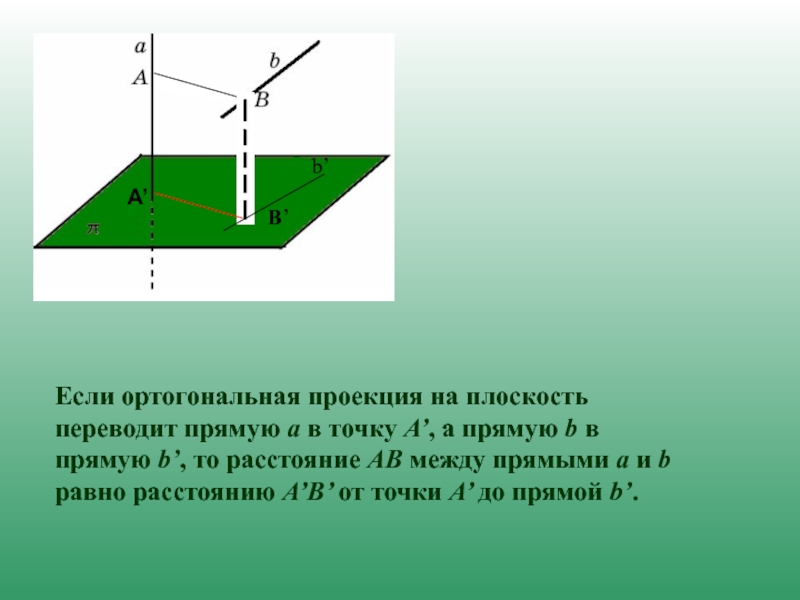
Слайд 9Если ортогональная проекция на плоскость переводит прямую a в точку A’,
В’
b’
А’
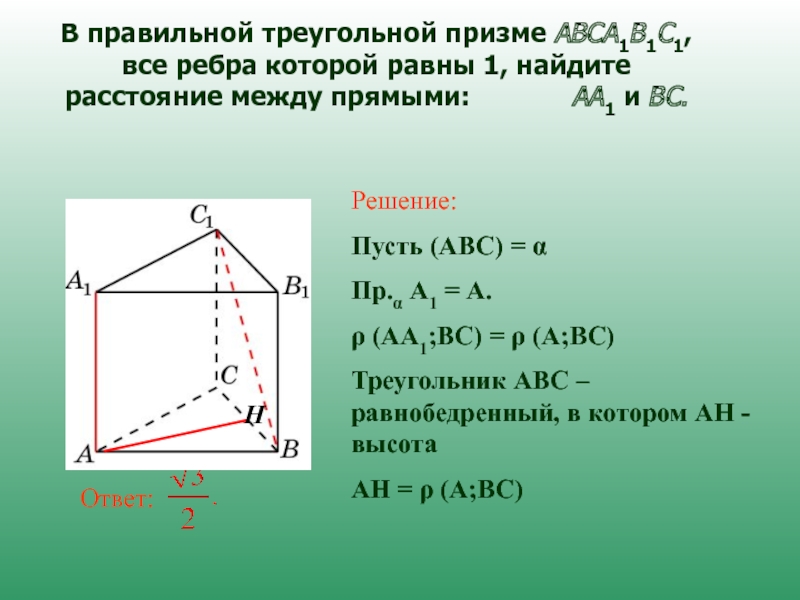
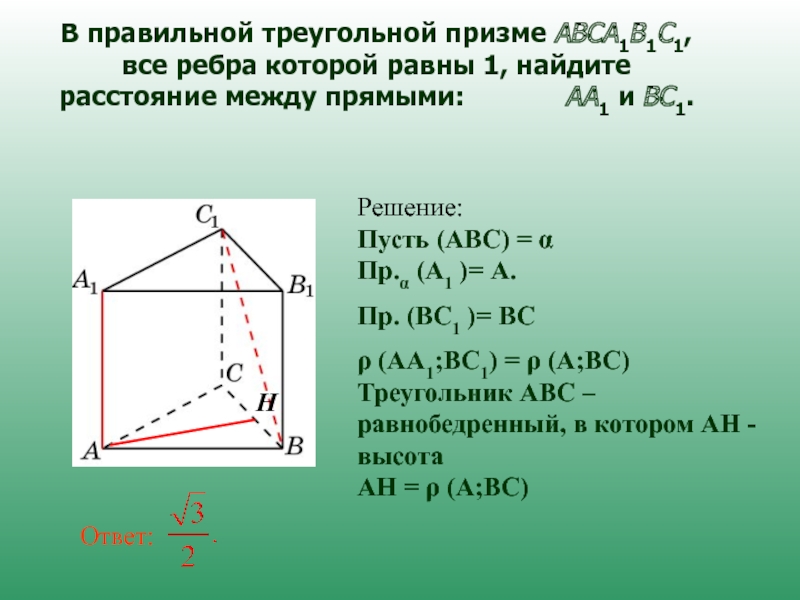
Слайд 10В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
Решение:
Пусть (АВС) = α
Пр.α А1 = А.
ρ (АА1;ВС) = ρ (А;ВС)
Треугольник АВС – равнобедренный, в котором АН - высота
АН = ρ (А;ВС)
Н
Слайд 11В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
Решение:
Пусть (АВС) = α
Пр.α (А1 )= А.
Пр. (ВС1 )= ВС
ρ (АА1;ВС1) = ρ (А;ВС)
Треугольник АВС – равнобедренный, в котором АН - высота
АН = ρ (А;ВС)
Н
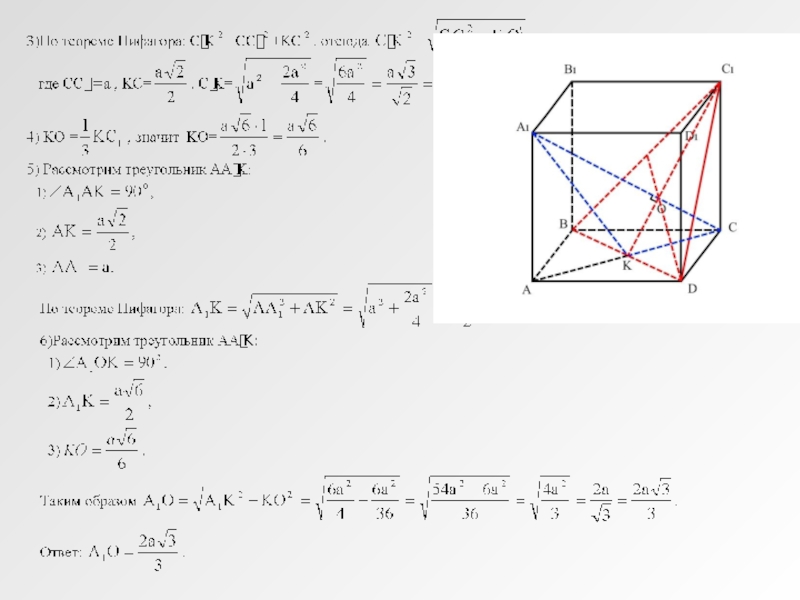
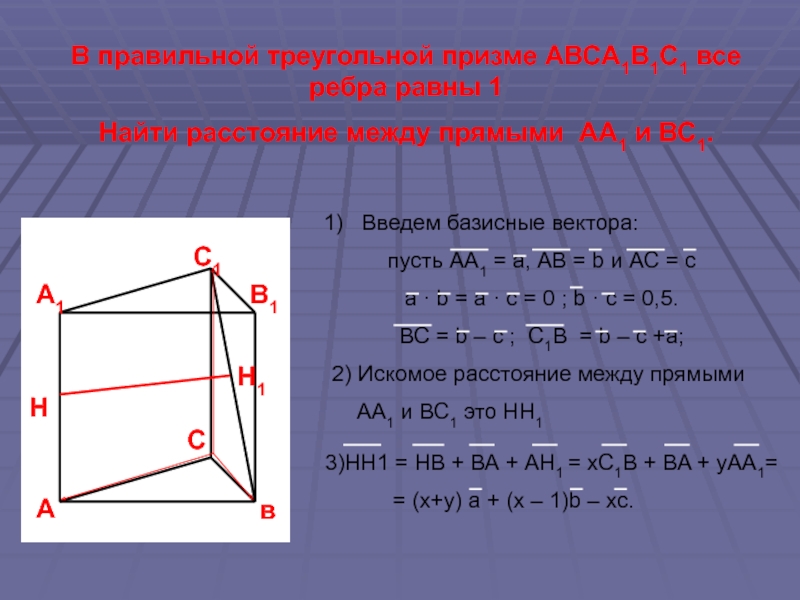
Слайд 12В правильной треугольной призме АВСА1В1С1 все ребра равны 1
Найти расстояние между
Введем базисные вектора:
пусть АА1 = а, АВ = b и АС = с
а · b = a · c = 0 ; b · c = 0,5.
BC = b – c ; C1B = b – c +a;
2) Искомое расстояние между прямыми
АА1 и ВС1 это НН1
3)НН1 = НВ + ВА + АН1 = xC1B + BA + yAA1=
= (x+y) a + (x – 1)b – xc.
Н
Н1
в
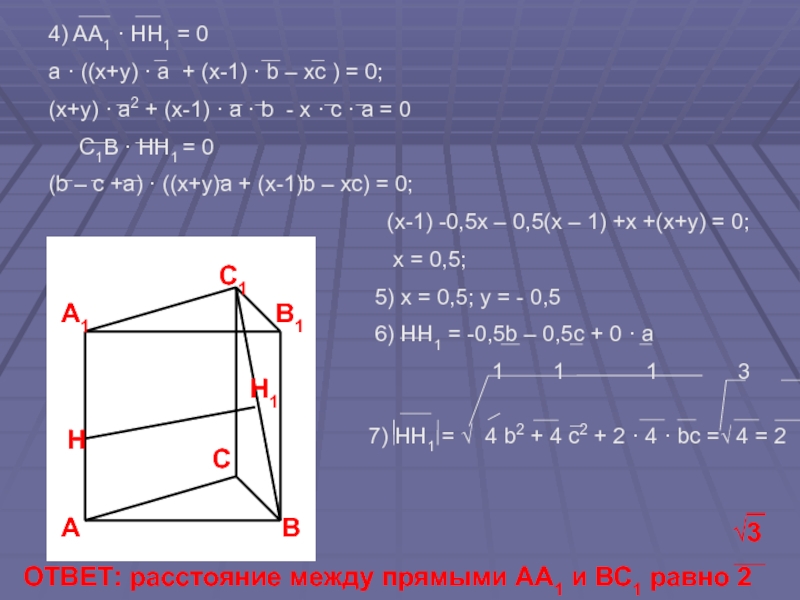
Слайд 134) AA1 · HH1 = 0
a · ((x+y) · a +
(x+y) · a2 + (x-1) · a · b - x · c · a = 0
C1B · HH1 = 0
(b – c +a) · ((x+y)a + (x-1)b – хc) = 0;
(x-1) -0,5x – 0,5(x – 1) +x +(x+y) = 0;
x = 0,5;
5) x = 0,5; y = - 0,5
6) HH1 = -0,5b – 0,5c + 0 · a
1 1 1 3 √3
7) HH1 = √ 4 b2 + 4 c2 + 2 · 4 · bc =√ 4 = 2
√3
ОТВЕТ: расстояние между прямыми АА1 и ВС1 равно 2
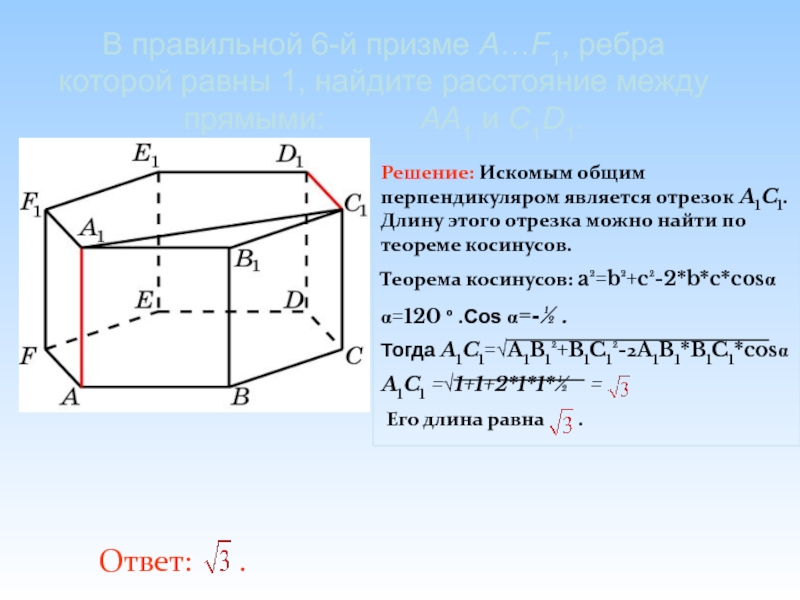
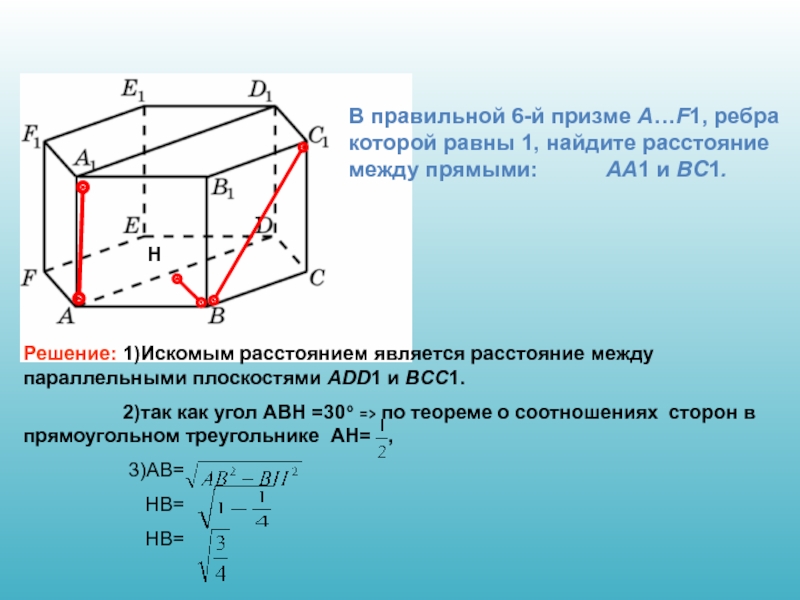
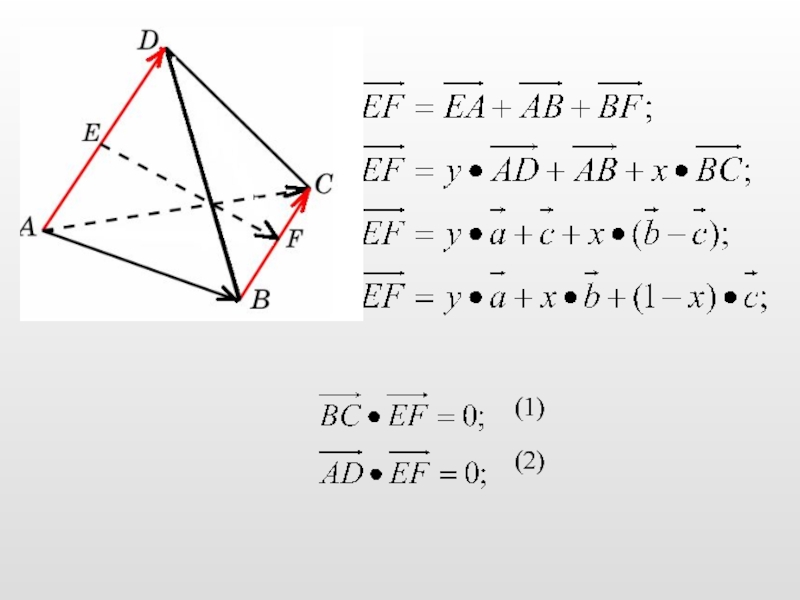
Слайд 14В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние
Слайд 15В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние
Слайд 16В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние
Решение: 1)Искомым расстоянием является расстояние между параллельными плоскостями ADD1 и BCC1.
2)так как угол ABH =30º => по теореме о соотношениях сторон в прямоугольном треугольнике AH= ,
3)AB=
НB=
НB=
Н
Слайд 17Ответ:
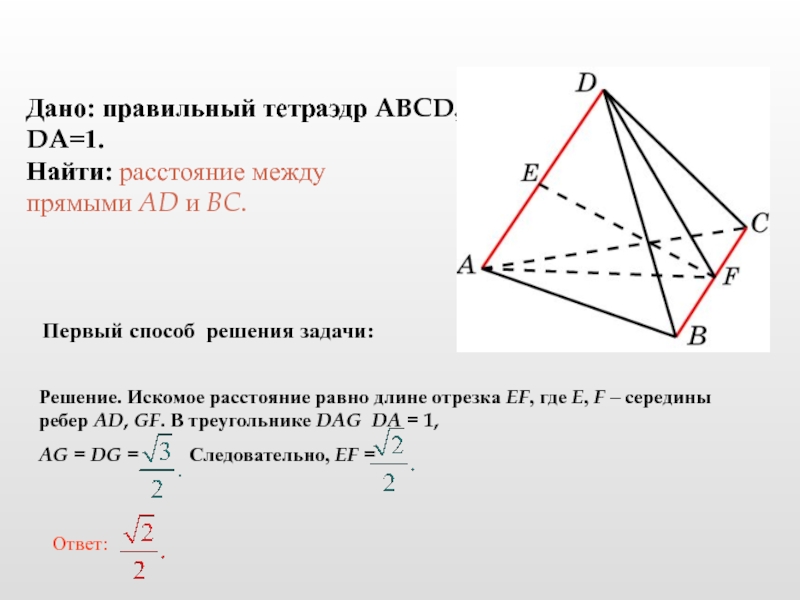
Решение. Искомое расстояние равно длине отрезка EF, где E, F
AG = DG = Следовательно, EF =
Первый способ решения задачи:
Дано: правильный тетраэдр ABCD,
DA=1.
Найти: расстояние между
прямыми AD и BC.
Слайд 22
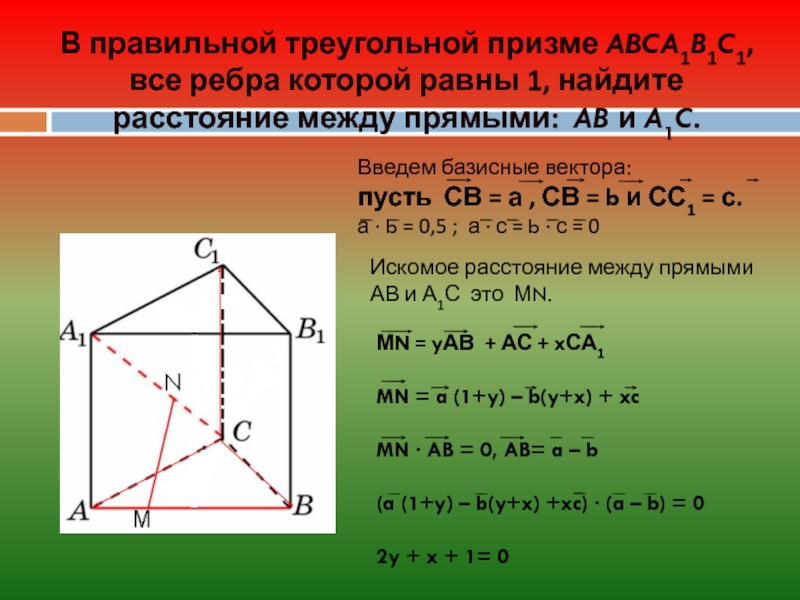
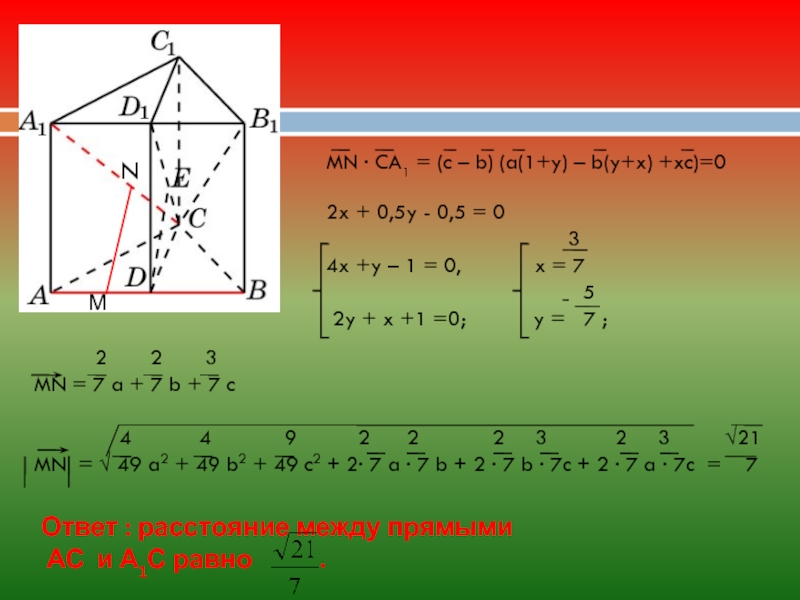
В правильной треугольной призме ABCA1B1C1, все ребра которой равны
Введем базисные вектора:
пусть СВ = а , СВ = b и СС1 = с.
а ∙ b = 0,5 ; а ∙ с = b ∙ с = 0
Искомое расстояние между прямыми АВ и А1С это МN.
МN = yАВ + АС + xСА1
MN = a (1+y) – b(y+x) + xc
MN ∙ AB = 0, AB= a – b
(a (1+y) – b(y+x) +xc) ∙ (a – b) = 0
2y + x + 1= 0
Слайд 23 2 2
MN = 7 a + 7 b + 7 c
4 4 9 2 2 2 3 2 3 √21
MN = √ 49 a2 + 49 b2 + 49 c2 + 2∙ 7 a ∙ 7 b + 2 ∙ 7 b ∙ 7c + 2 ∙ 7 a ∙ 7c = 7
Ответ : расстояние между прямыми
АС и А1С равно .
MN ∙ CA1 = (c – b) (a(1+y) – b(y+x) +xc)=0
2x + 0,5y - 0,5 = 0
3
4x +y – 1 = 0, x = 7
5
2y + x +1 =0; y = 7 ;
Слайд 24
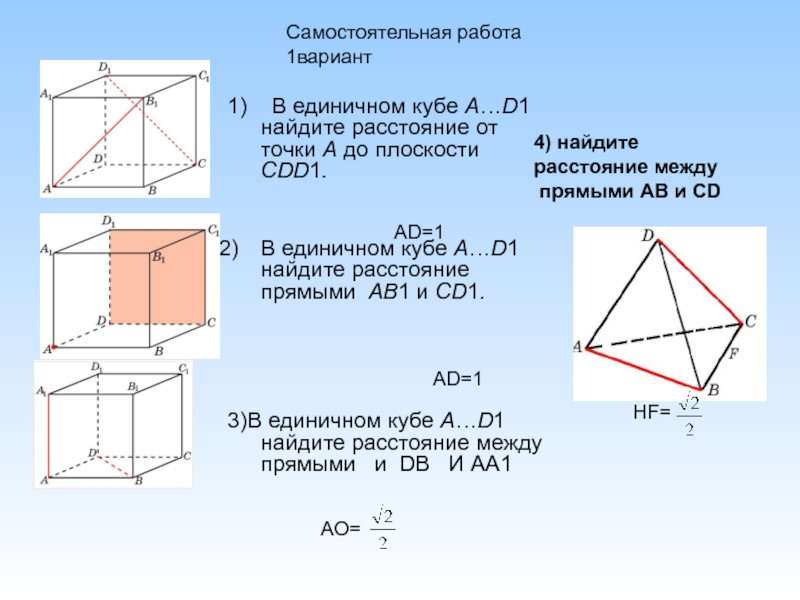
1) В единичном кубе A…D1 найдите расстояние от точки A
В единичном кубе A…D1 найдите расстояние прямыми AB1 и CD1.
3)В единичном кубе A…D1 найдите расстояние между прямыми и DB И АА1
АD=1
АО=
АD=1
Самостоятельная работа
1вариант
4) найдите
расстояние между
прямыми АВ и СD
HF=
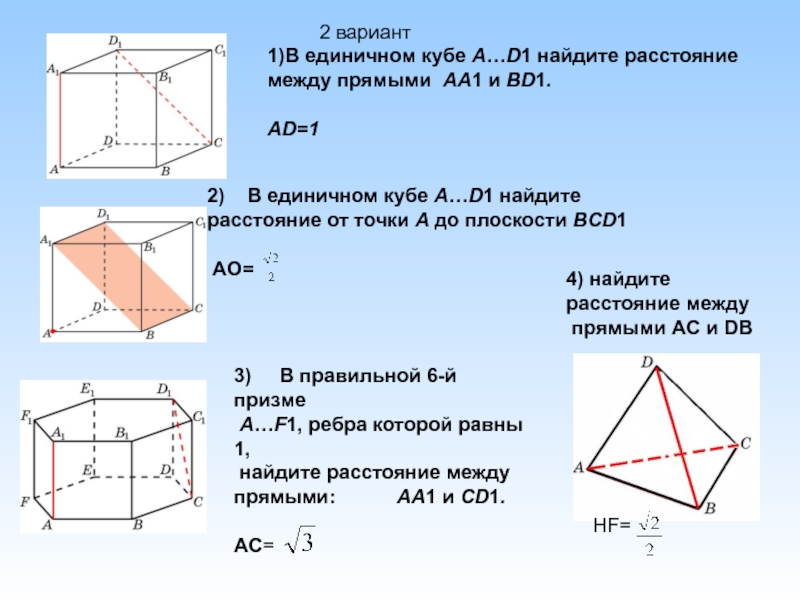
Слайд 253) В правильной 6-й призме
A…F1, ребра которой равны
найдите расстояние между
прямыми: AA1 и CD1.
AC=
2) В единичном кубе A…D1 найдите
расстояние от точки A до плоскости BCD1
AO=
1)В единичном кубе A…D1 найдите расстояние
между прямыми AA1 и BD1.
АD=1
2 вариант
4) найдите
расстояние между
прямыми AC и DB
HF=
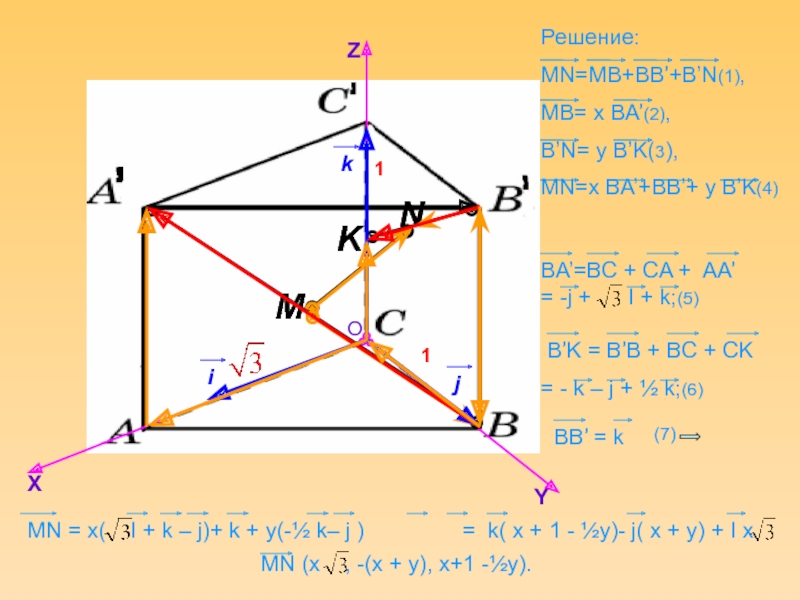
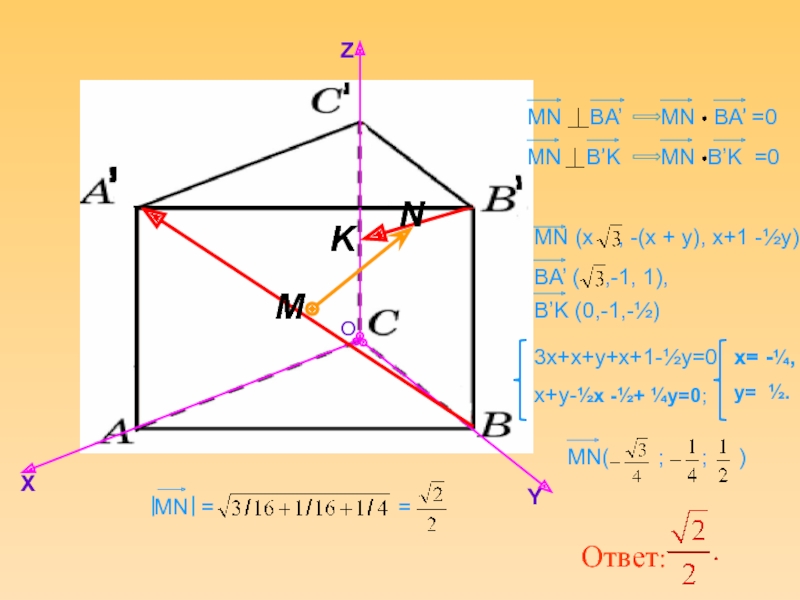
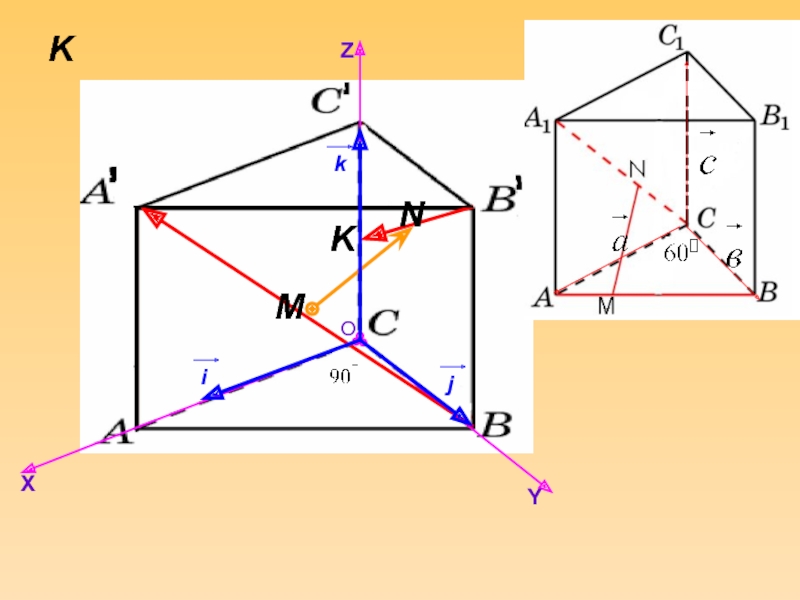
Слайд 26Основанием прямой призмы
является треугольник АВС, в котором угол С=
Угол А= , ВС=1. Точка К середина ребра СС’, а
Тангенс угла между прямой А’В и плоскостью основания равен 1.
Найдите расстояние между прямыми В’К и А’В .
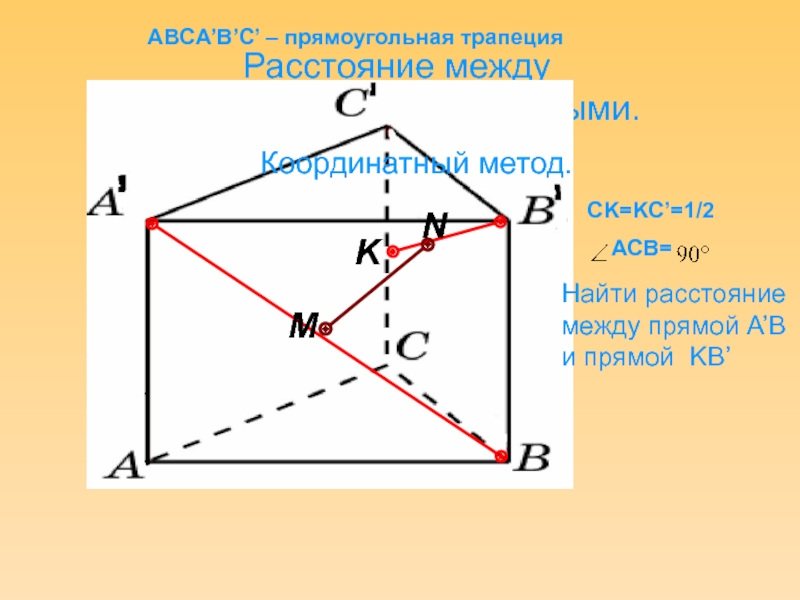
Слайд 27Расстояние между скрещивающимися прямыми.
ABCA’B’C’ – прямоугольная трапеция
Найти расстояние между прямой A’B
Координатный метод.
Слайд 31
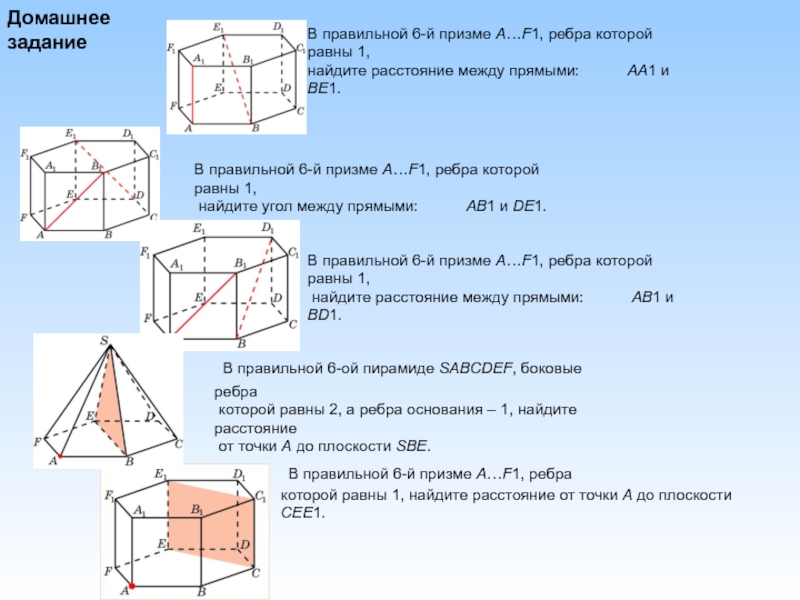
Домашнее задание
В правильной 6-й призме A…F1, ребра которой равны 1,
найдите расстояние между прямыми: AA1 и BE1.
В правильной 6-й призме A…F1, ребра которой равны 1,
найдите угол между прямыми: AB1 и DE1.
В правильной 6-й призме A…F1, ребра которой равны 1,
найдите расстояние между прямыми: AB1 и BD1.
В правильной 6-ой пирамиде SABCDEF, боковые ребра
которой равны 2, а ребра основания – 1, найдите расстояние
от точки A до плоскости SBE.
В правильной 6-й призме A…F1, ребра
которой равны 1, найдите расстояние от точки A до плоскости CEE1.