- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
28.01.2013 Классная работа презентация
Содержание
- 1. 28.01.2013 Классная работа
- 2. Цель урока. 1.
- 3. Идея развития "Величие
- 4. Теоретический тест
- 5. 1) Медиана в равнобедренном треугольнике является его
- 6. 2) Если треугольник равносторонний, то: а) он
- 7. 3) В каком треугольнике только одна его
- 8. 4) Биссектриса в равностороннем треугольнике является медианой
- 9. 5) Если треугольник равнобедренный, то: а)
- 10. 6) В каком треугольнике любая его высота
- 11. Ответы: 1б; 2абв; 3б;
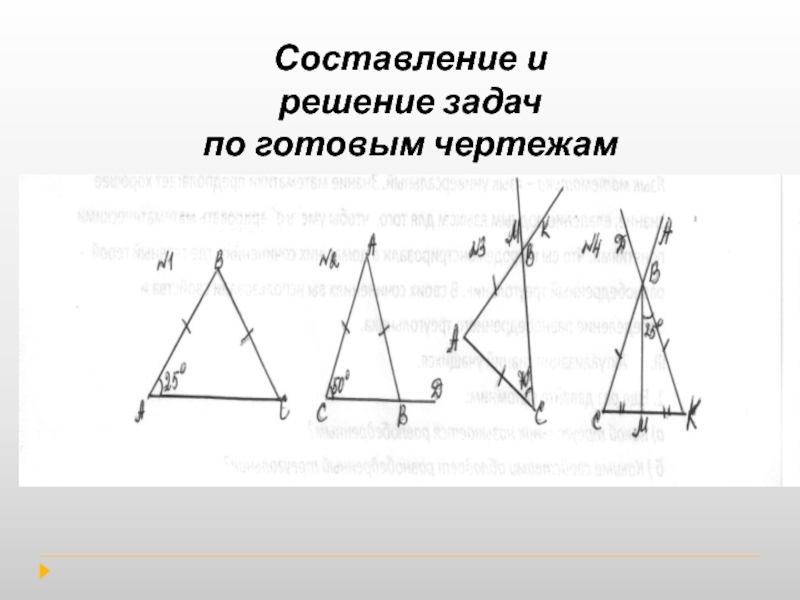
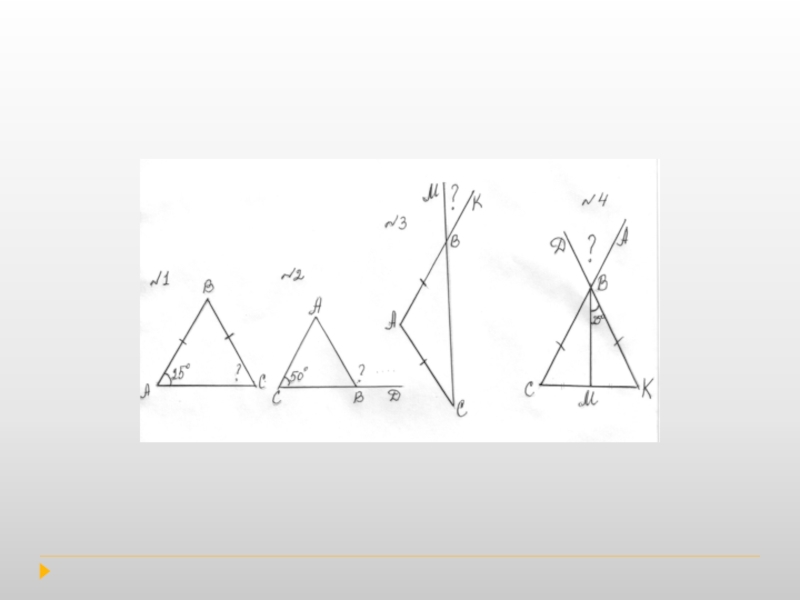
- 12. Составление и решение задач по готовым чертежам
- 14. Самостоятельная работа Вариант 1 1.
- 15. Правильные ответы Вариант 1 Задача 1.
- 16. Домашнее задание №117, 119.
- 17. Подведение итогов урока А теперь, ребята ,
Слайд 2Цель урока.
1. Закрепить навыки и умения учащихся
2. Научить по готовым чертежам составлять и решать задачи.
3. Развивать логическое мышление, математическую речь учащихся.
3. Воспитывать аккуратность при построении чертежей
Слайд 51) Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Слайд 62) Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в)
Слайд 73) В каком треугольнике только одна его высота делит треугольник на
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Слайд 84) Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а)
б) может быть верно;
в) всегда неверно.
Слайд 95) Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая его медиана является
в) ответы а) и б) неверны.
Слайд 106) В каком треугольнике любая его высота делит треугольник на два
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Слайд 14Самостоятельная работа
Вариант 1
1. Периметр равнобедренного треугольника равен 34 см. Найти
2. В равнобедренном треугольнике ABC с основанием AC на медиане выбрана точка M. Доказать равенство треугольников ABM и CBM.
Вариант 2
1. Периметр равнобедренного треугольника равен 28 см. Найти стороны треугольника, если его основание на 4 см больше боковой стороны.
2. В равнобедренном треугольнике ABC с основанием AC на высоте BD выбрана точка M. Доказать равенство треугольников AMD и CMD.
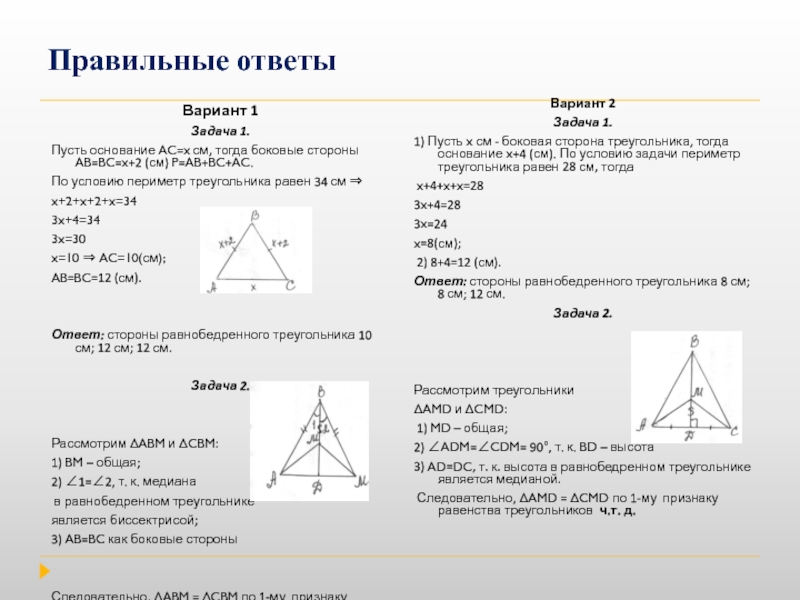
Слайд 15Правильные ответы
Вариант 1
Задача 1.
Пусть основание AC=x см, тогда боковые стороны
По условию периметр треугольника равен 34 см ⇒
x+2+x+2+x=34
3x+4=34
3x=30
x=10 ⇒ AC=10(см);
AB=BC=12 (см).
Ответ: стороны равнобедренного треугольника 10 см; 12 см; 12 см.
Задача 2.
Рассмотрим ΔABM и ΔCBM:
1) BM – общая;
2) ∠1=∠2, т. к. медиана
в равнобедренном треугольнике
является биссектрисой;
3) AB=BC как боковые стороны
Следовательно, ΔABM = ΔCBM по 1-му признаку равенства треугольников ч.т. д.
Вариант 2
Задача 1.
1) Пусть x см - боковая сторона треугольника, тогда основание x+4 (см). По условию задачи периметр треугольника равен 28 см, тогда
x+4+x+x=28
3x+4=28
3x=24
x=8(см);
2) 8+4=12 (см).
Ответ: стороны равнобедренного треугольника 8 см; 8 см; 12 см.
Задача 2.
Рассмотрим треугольники
ΔAMD и ΔCMD:
1) MD – общая;
2) ∠ADM=∠CDM= 90°, т. к. BD – высота
3) AD=DC, т. к. высота в равнобедренном треугольнике является медианой.
Следовательно, ΔAMD = ΔCMD по 1-му признаку равенства треугольников ч.т. д.
Слайд 17Подведение итогов урока
А теперь, ребята , ответьте на вопросы:
Я понял, что
Я задумался над …
Я не понял, что …, но