- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многогранники презентация
Содержание
- 1. Правильные многогранники
- 2. С глубокой древности человеку известны пять удивительных многогранников
- 3. По числу граней их называют правильный тетраэдр (четырёхгранник)
- 4. гексаэдр (шестигранник) или куб
- 5. октаэдр (восьмигранник)
- 6. додекаэдр (двенадцатигранник)
- 7. икосаэдр (двадцатигранник)
- 8. Свойства этих многогранников изучали ученые и священники,
- 9. Великий древнегреческий философ Платон, живший в IV
- 10. Четыре сущности природы были известны человечеству: огонь,
- 11. атом огня имел вид тетраэдра, земли
- 12. Но оставался додекаэдр, которому не было соответствия
- 13. Платон и его ученики в своих работах
- 14. Определение правильного многогранника Многогранник называется правильным, если
- 15. Платоновы тела - трехмерный аналог плоских правильных
- 16. Доказательство этого факта известно уже более двух
- 17. Существует лишь пять выпуклых правильных многогранников -
- 18. Характеристики правильных многогранников
- 19. Развертки правильных многогранников
- 20. Двойственность правильных многогранников Гексаэдр (куб) и октаэдр
- 21. Возьмем любой куб и рассмотрим многогранник с
- 22. Центры граней октаэдра служат вершинами куба
- 23. Икосаэдр и додекаэдр также являются двойственными многогранниками
- 24. Двойственным многогранником к тетраэдру является сам тетраэдр
С глубокой древности человеку известны пять удивительных многогранников
Слайд 8Свойства этих многогранников изучали ученые и священники, их модели можно было
увидеть в работах архитекторов и ювелиров, им приписывались различные магические и целебные свойства
Слайд 9Великий древнегреческий философ Платон, живший в IV – V вв. до
нашей эры, считал, что эти тела олицетворяют сущность природы
Слайд 10Четыре сущности природы были известны человечеству: огонь, вода, земля и воздух.
По мнению Платона, их атомы имели вид правильных многогранников
Слайд 12Но оставался додекаэдр, которому не было соответствия
Платон предположил, что существует
ещё одна (пятая) сущность. Он назвал её мировым эфиром. Атомы этой пятой сущности и имели вид додекаэдра
Слайд 13Платон и его ученики в своих работах большое внимание уделяли перечисленным
многогранникам. Поэтому эти многогранники называют также платоновыми телами
Слайд 14Определение правильного многогранника
Многогранник называется правильным, если все его грани – равные
между собой правильные многогранники, из каждой вершины выходит одинаковое число ребер и все двугранные углы равны
Слайд 15 Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным
и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников
Слайд 16 Доказательство этого факта известно уже более двух тысяч лет; этим доказательством
и изучением пяти правильных тел завершаются "Начала" Евклида
Слайд 17Существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр
с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями
Слайд 20Двойственность правильных многогранников
Гексаэдр (куб) и октаэдр образуют двойственную пару многогранников. Число
граней одного многогранника равно числу вершин другого и наоборот.
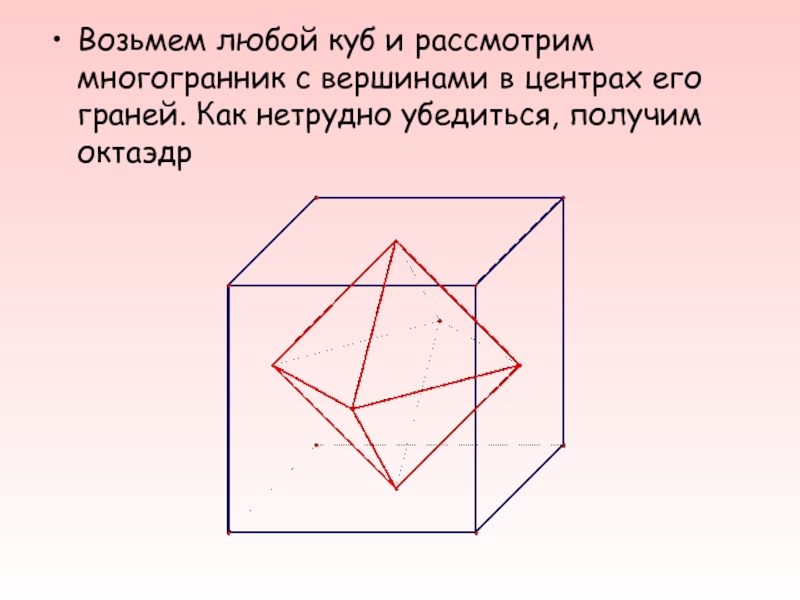
Слайд 21Возьмем любой куб и рассмотрим многогранник с вершинами в центрах его
граней. Как нетрудно убедиться, получим октаэдр