- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика на шахматной доске презентация
Содержание
- 1. Математика на шахматной доске
- 2. Шахматы не только популярная игра, но
- 3. Приведем три маршрута.
- 4. Задачи о маршрутах составлены и для других
- 5. Задача 2. Сколькими способами можно расставить на
- 6. Сначала выясняется, какое наибольшее число фигур не
- 7. Другой класс задач на расстановки связан с
- 8. Для охраны доски меньшим, чем пять, числом
- 9. Играйте в шахматы и решайте задачи по комбинаторике!
Шахматы не только популярная игра, но и источник множества интересных математических задач. Не случайно шахматные термины можно встретить в литературе по комбинаторике , теории графов, кибернетике, теории игр, программированию .
Слайд 2 Шахматы не только популярная игра, но и источник множества интересных
математических задач. Не случайно шахматные термины можно встретить в литературе по комбинаторике , теории графов, кибернетике, теории игр, программированию . Расскажем о нескольких математических задачах на шахматной доске.
Задача 1.
Обойти конем все поля доски,
посетив каждое из них по од-
ному разу.
Этой задачей занимался Л.Эйлер
Задача 1.
Обойти конем все поля доски,
посетив каждое из них по од-
ному разу.
Этой задачей занимался Л.Эйлер
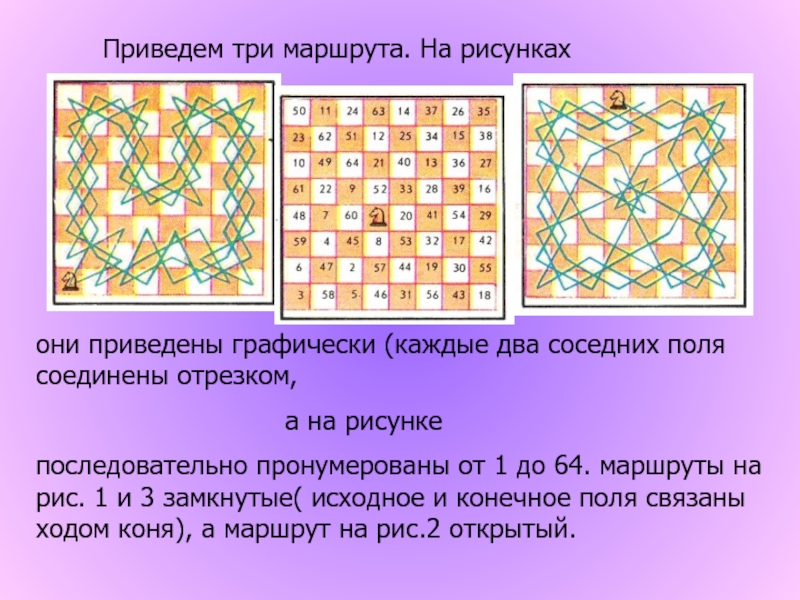
Слайд 3 Приведем три маршрута. На рисунках
они приведены графически (каждые два соседних поля соединены отрезком,
а на рисунке
последовательно пронумерованы от 1 до 64. маршруты на рис. 1 и 3 замкнутые( исходное и конечное поля связаны ходом коня), а маршрут на рис.2 открытый.
Слайд 4Задачи о маршрутах составлены и для других фигур.
На рис.
изображен кратчайший
замкнутый маршрут
ферзя по всей доске,
занимающий 14 ходов.
замкнутый маршрут
ферзя по всей доске,
занимающий 14 ходов.
Слайд 5Задача 2. Сколькими способами можно расставить на доске 8 ферзей так.
Чтобы они не угрожали друг другу (никакие два из их не стояли бы на одной линии) ?
Существует 92 требуемые расста-
новки (докажите), причем они
получаются из 12 основных
поворотами и зеркальными
отражениями доски.
Одно из решений:
Слайд 6Сначала выясняется, какое наибольшее число фигур не угрожает на доске друг
другу, а затем- сколько имеется расстановок.
Ладей, как и ферзей,
можно расставить максимум
8 (всего 8!=40320 расстановок).
Максимальное число не угрожа-
ющих друг другу слонов равно
14 (256 расстановок),
Коней -32, королей- 16
(281571 расстановка).
Ладей, как и ферзей,
можно расставить максимум
8 (всего 8!=40320 расстановок).
Максимальное число не угрожа-
ющих друг другу слонов равно
14 (256 расстановок),
Коней -32, королей- 16
(281571 расстановка).
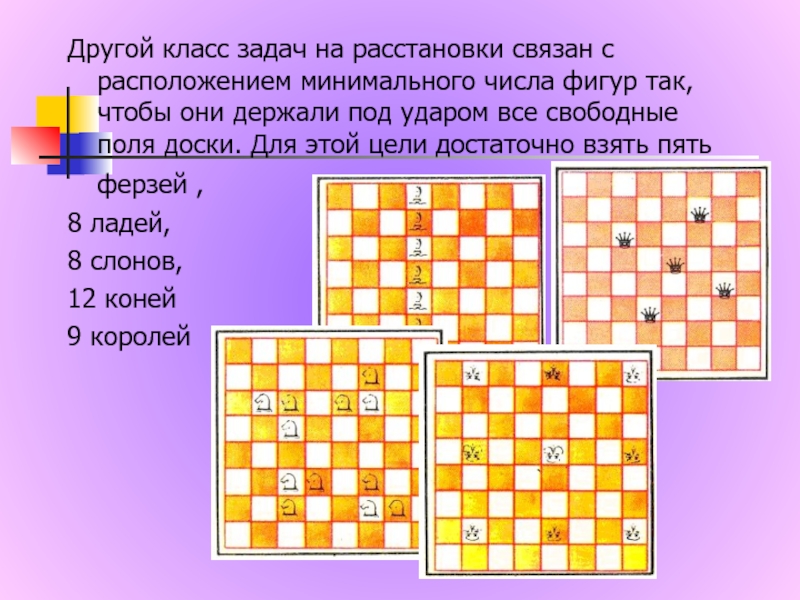
Слайд 7Другой класс задач на расстановки связан с расположением минимального числа фигур
так, чтобы они держали под ударом все свободные
поля доски. Для этой цели достаточно взять пять ферзей ,
8 ладей,
8 слонов,
12 коней
9 королей
8 ладей,
8 слонов,
12 коней
9 королей
Слайд 8Для охраны доски меньшим, чем пять, числом фигур не обойтись, однако
их состав можно «ослабить», заменив двух ферзей ладьями или
даже ладьей с королем или
слоном:
слоном:
