- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предел функции на бесконечности презентация
Содержание
Слайд 2План урока
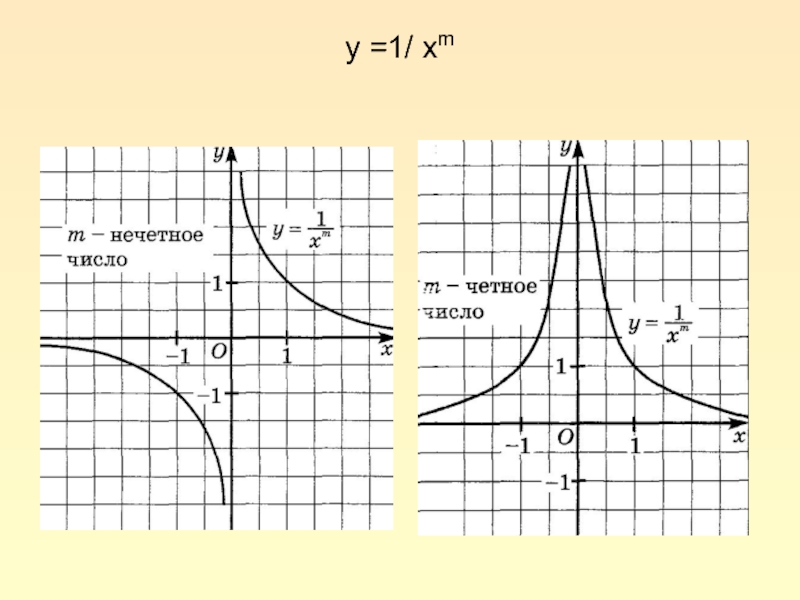
Графики функций y=1/x и y=1/x2.
Графики функций y=1/xm, для
m четных и нечетных.
Понятие асимптоты.
Понятия предела функции на +∞, -∞, ∞.
Геометрический смысл предела функции на +∞, -∞, ∞.
Правила вычисления пределов функции на ∞.
Формулы вычисления предела функции на ∞.
Приемы вычисления пределов функции на ∞.
Понятие асимптоты.
Понятия предела функции на +∞, -∞, ∞.
Геометрический смысл предела функции на +∞, -∞, ∞.
Правила вычисления пределов функции на ∞.
Формулы вычисления предела функции на ∞.
Приемы вычисления пределов функции на ∞.
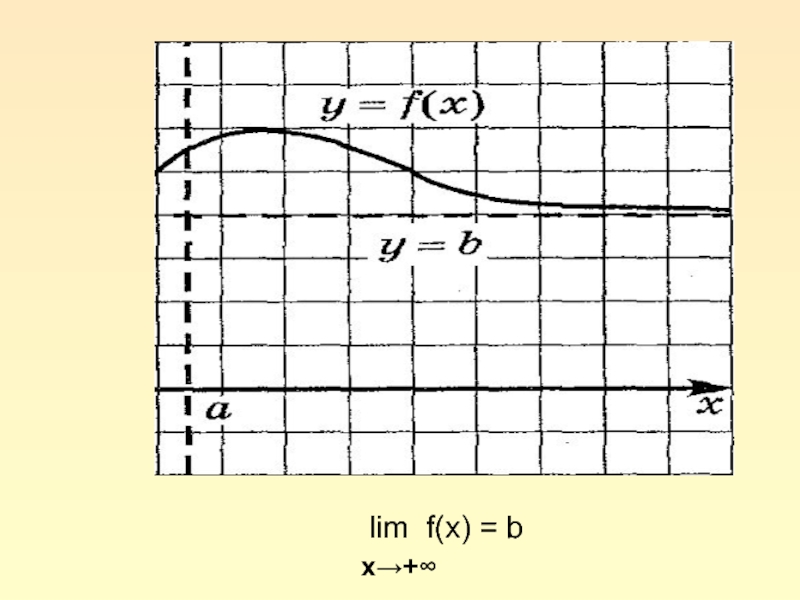
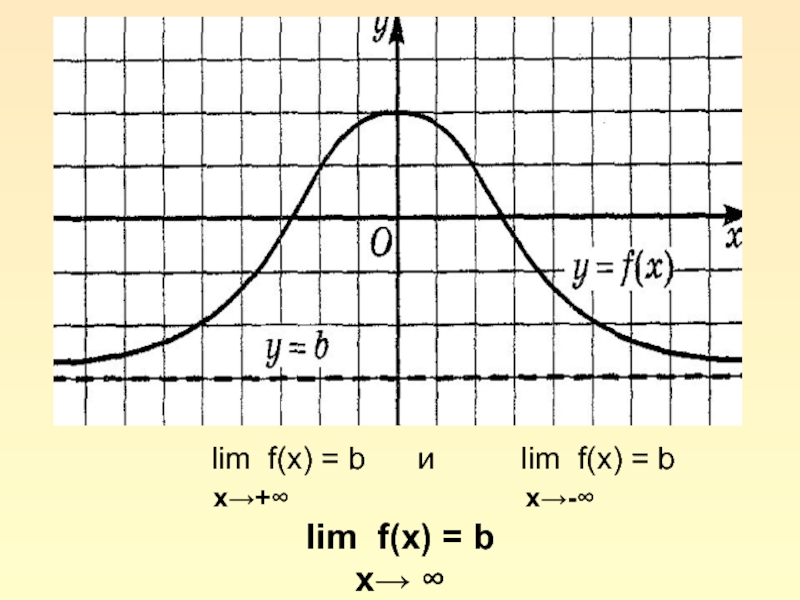
Слайд 7 Существование
lim f(x) = b
x→ ∞
эквивалентно наличию
горизонтальной асимптоты
у графика функции y = f(x)
x→ ∞
эквивалентно наличию
горизонтальной асимптоты
у графика функции y = f(x)
Слайд 8Правила вычисления пределов
Если lim f(x) = b
и lim g(x) =c , то
x→∞ x→∞
1) Предел суммы равен сумме пределов:
lim (f(x)+ g(x)) = b+ c
x→∞
2) Предел произведения равен произведению пределов:
lim f(x)·g(x) = b·c
x→∞
3) Предел частного равен частному пределов:
lim f(х):g(x) = b:c
x→∞
4) Постоянный множитель можно вынести за знак предела:
lim k· f(x) = k · b
x→∞
x→∞ x→∞
1) Предел суммы равен сумме пределов:
lim (f(x)+ g(x)) = b+ c
x→∞
2) Предел произведения равен произведению пределов:
lim f(x)·g(x) = b·c
x→∞
3) Предел частного равен частному пределов:
lim f(х):g(x) = b:c
x→∞
4) Постоянный множитель можно вынести за знак предела:
lim k· f(x) = k · b
x→∞
Слайд 9Формулы для вычисления предела функции на бесконечности
lim (1/x)= 0,
x→ ∞
lim (1/xm) = 0
x→ ∞
lim (k/xm) = 0
x→ ∞
Прием вычисления пределов
функции на бесконечности
стр. 149 учебника
x→ ∞
lim (1/xm) = 0
x→ ∞
lim (k/xm) = 0
x→ ∞
Прием вычисления пределов
функции на бесконечности
стр. 149 учебника
Слайд 10Итог урока
Что означает существование предела функции на бесконечности?
Какую асимптоту имеет график
функции y=1/ x4 ?
Какие вы знаете правила для вычисления пределов функции на бесконечности?
С какими формулами вычисления пределов на бесконечности вы познакомились?
Как найти lim (5-3x3) / (6x3 +2)?
Какие вы знаете правила для вычисления пределов функции на бесконечности?
С какими формулами вычисления пределов на бесконечности вы познакомились?
Как найти lim (5-3x3) / (6x3 +2)?