в Великобритании Жаровой Милены
Учитель математики Щербакова В.Б.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площади геометрических фигур презентация
Содержание
- 1. Площади геометрических фигур
- 2. Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
- 3. 1. Равные многоугольники имеют равные площади Основные свойства площадей
- 4. 2. Если многоугольник составлен из нескольких многоугольников,
- 5. Формулы для нахождения площадей геометрических фигур
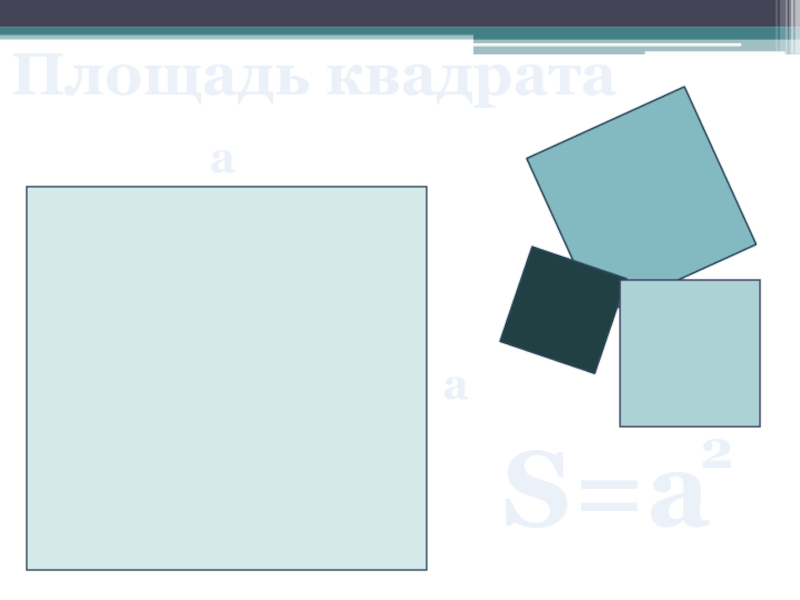
- 6. Площадь квадрата а а
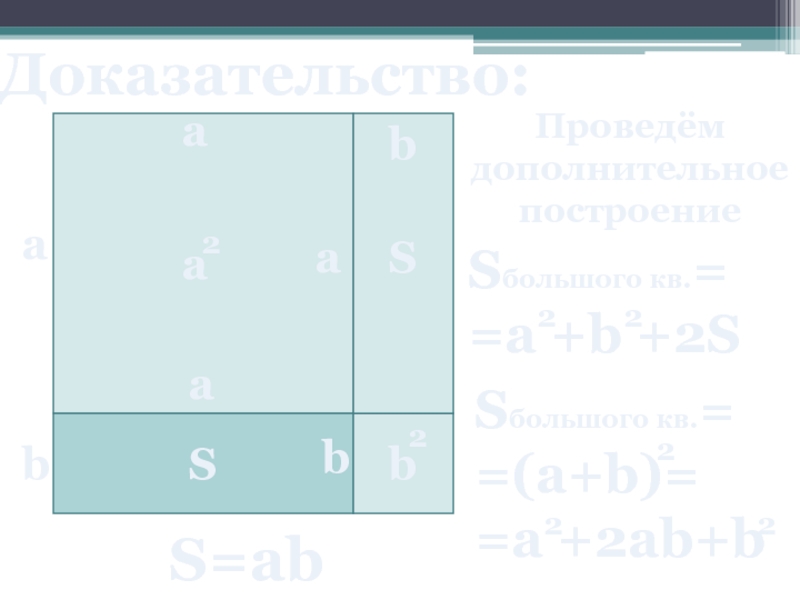
- 7. Доказательство: 1 S большого кв. =1 n– целое число
- 8. Площадь прямоугольника а b S=a∙b
- 9. Доказательство: a a
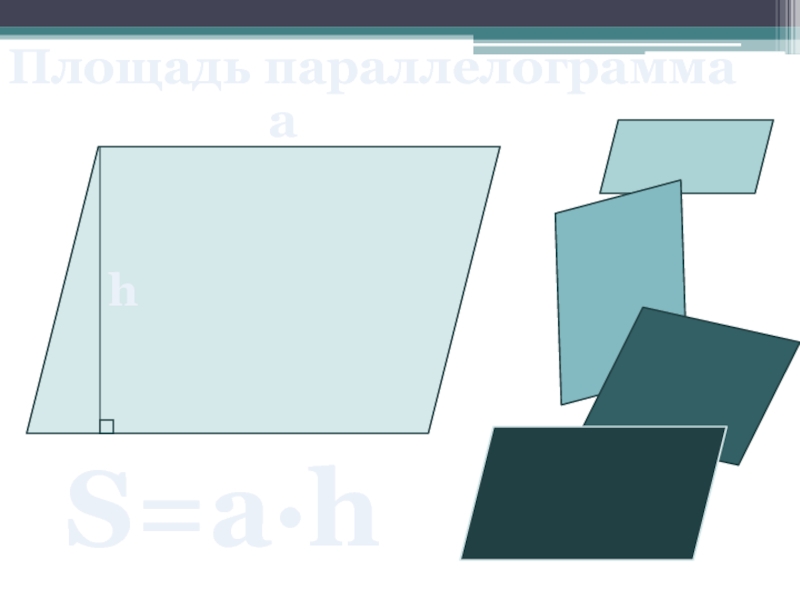
- 10. Площадь параллелограмма a h S=a∙h
- 11. Доказательство: A B C D Проведём
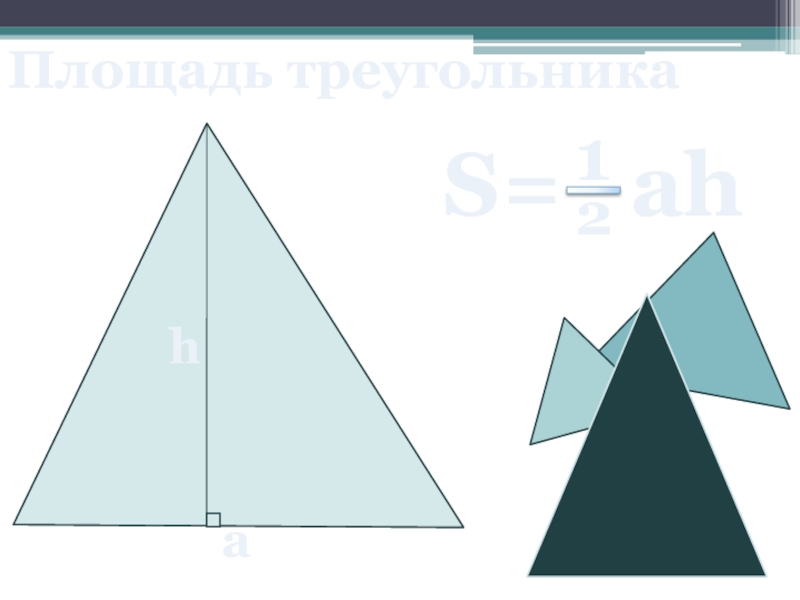
- 12. Площадь треугольника a h
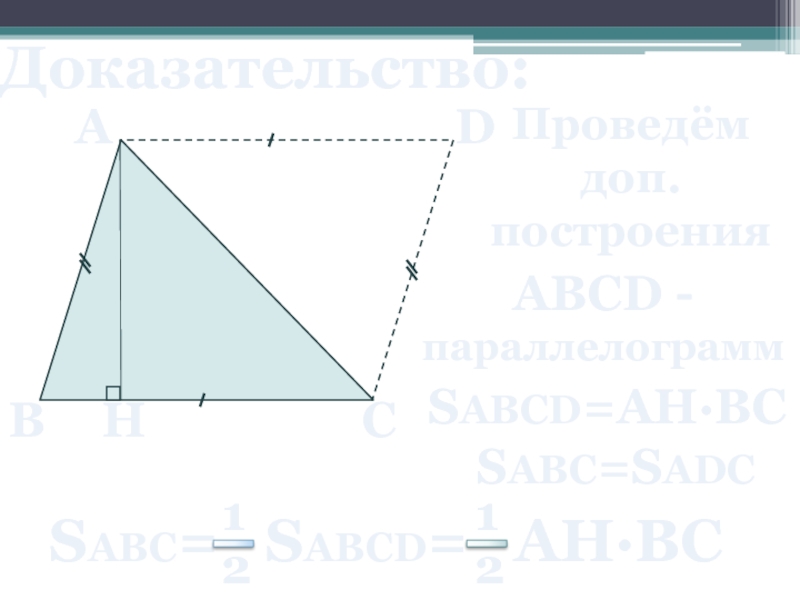
- 13. Доказательство: A B C Проведём доп. построения ABCD - параллелограмм SABCD=AH∙BC SABC=SADC
- 14. Следствие 1 Площадь прямоугольного треугольника равна половине произведения его катетов. A B C
- 15. Следствие 2 Если высоты двух треугольников равны,
- 16. Теорема об отношении площадей треугольников имеющих по
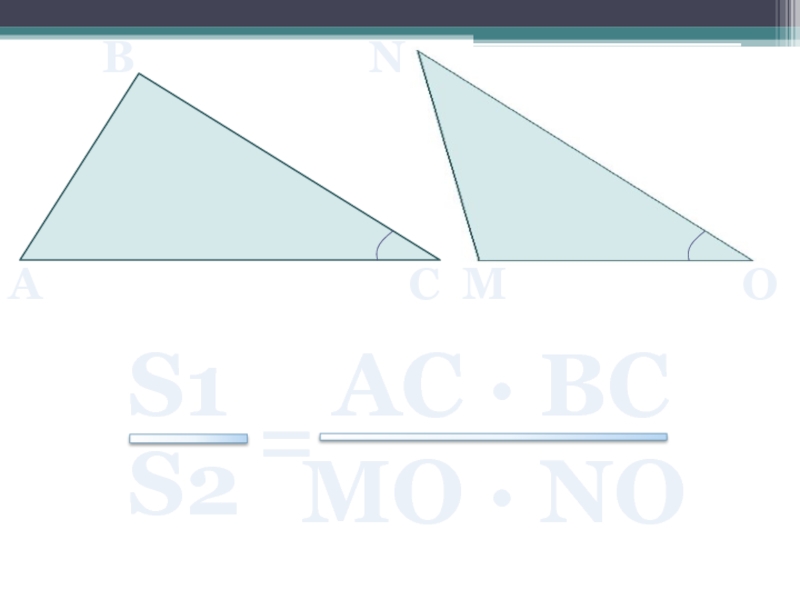
- 17. A B C M N O
- 18. Доказательство: H1 H2 BH1 –
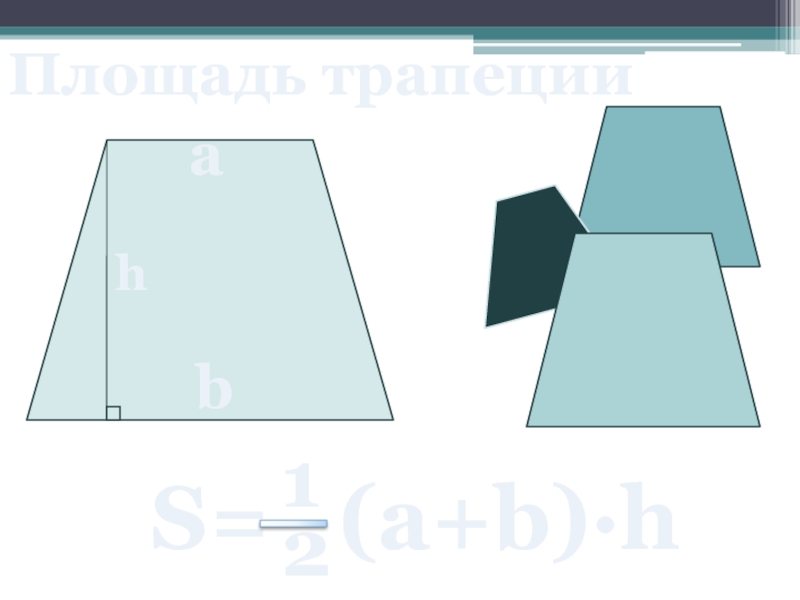
- 19. Площадь трапеции a b h
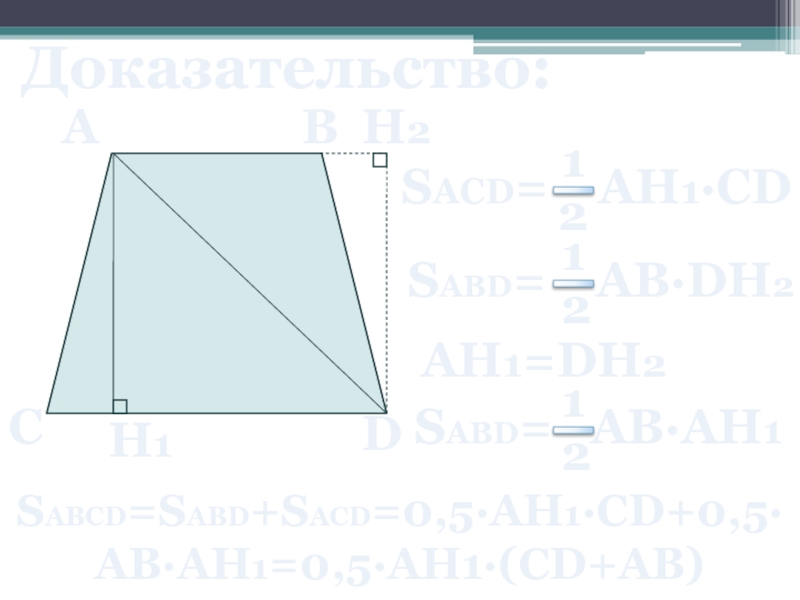
- 20. Доказательство: A B C D H1 H2 AH1=DH2 SABCD=SABD+SACD=0,5∙AH1∙CD+0,5∙ AB∙AH1=0,5∙AH1∙(CD+AB)
- 21. Дано:ABCD-трапеция AB=21 см CD=17
- 22. Дано:ABCD-трапеция AB=CD, B=135°KD=3,4 см; AK=1,4 см
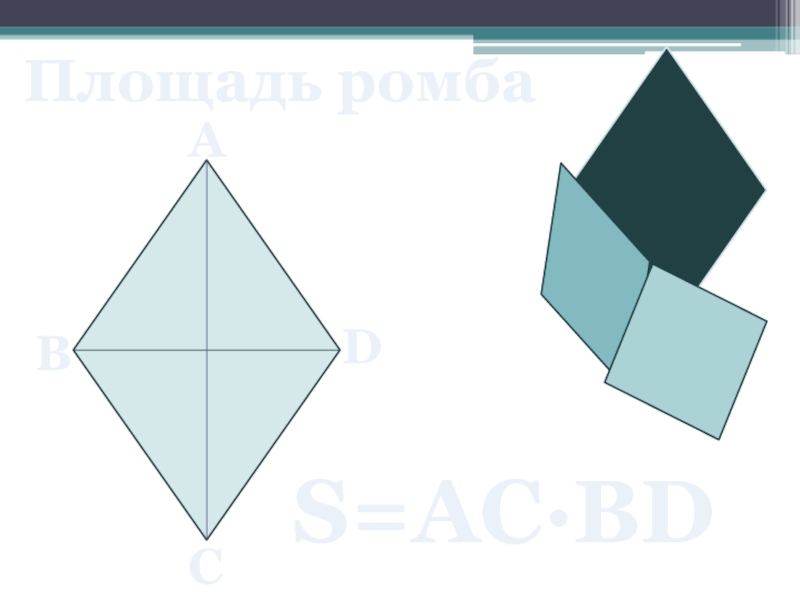
- 23. Площадь ромба A B C D S=AC∙BD
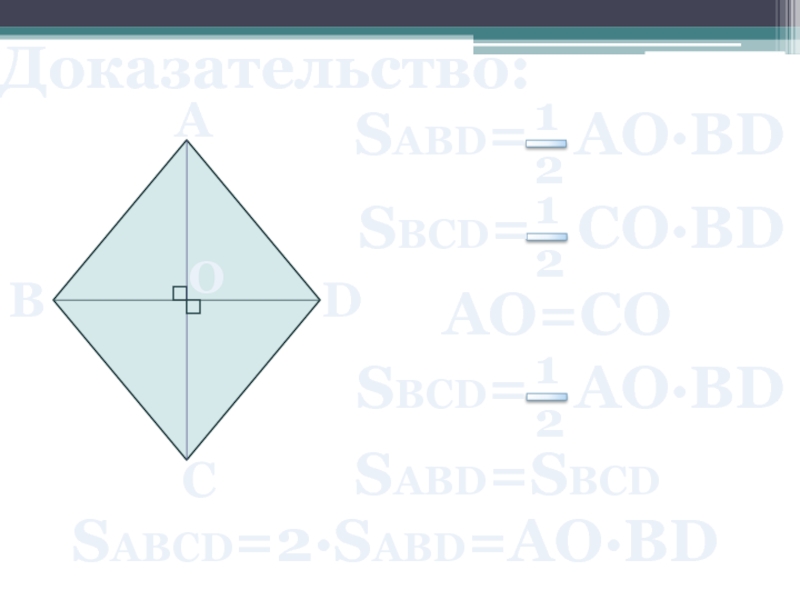
- 24. Доказательство: A B C D O AO=CO SABD=SBCD SABCD=2∙SABD=AO∙BD
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
Слайд 42. Если многоугольник составлен из нескольких многоугольников, то его площадь равна
сумме площадей этих многоугольников
S=S1+S2+S3
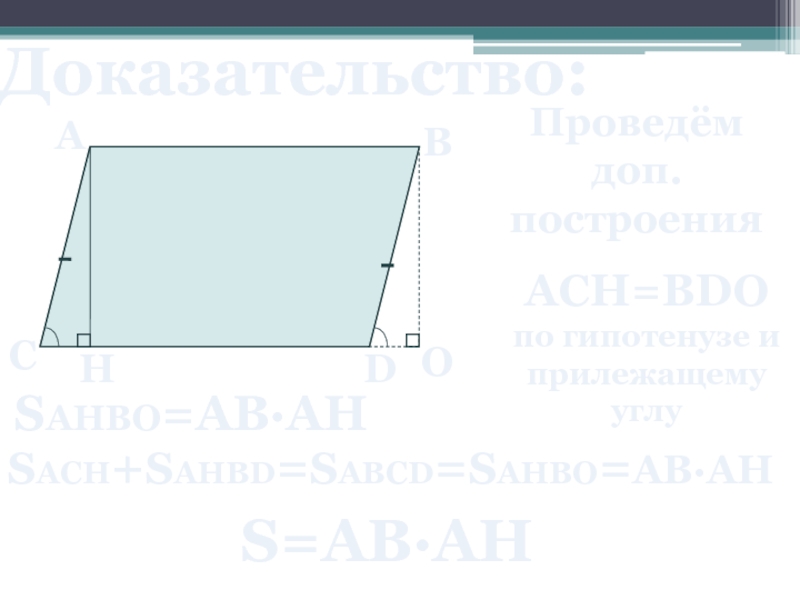
Слайд 11Доказательство:
A
B
C
D
Проведём доп. построения
ACH=BDO
по гипотенузе и прилежащему углу
SACH+SAHBD=SABCD=SAHBO=AB∙AH
SAHBO=AB∙AH
S=AB∙AH
Слайд 15Следствие 2
Если высоты двух треугольников равны, то их площади относятся как
основания.
h1
h2
a
b
h1=h2
Слайд 16Теорема об отношении площадей треугольников имеющих по равному углу
Если угол одного
треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
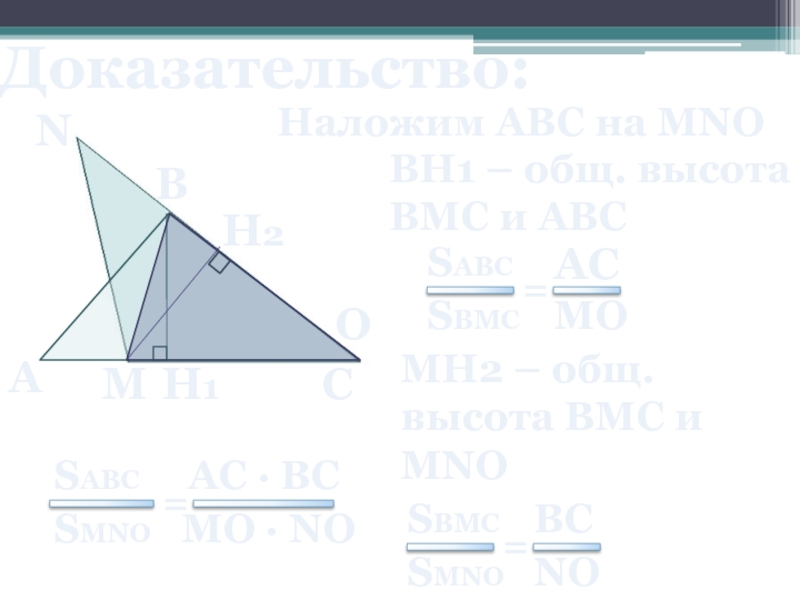
Слайд 18Доказательство:
H1
H2
BH1 – общ. высота BMC и ABC
Наложим ABC на MNO
MH2
– общ. высота BMC и MNO
Слайд 21Дано:ABCD-трапеция
AB=21 см
CD=17 см;
BH=7см-высота
Найти: S трапеции ABCD
Решение:
SABCD= BH×(AB+CD)÷2
SABCD= 7×(21+17)÷2=38×7÷2=19×7=133(см²)
Ответ:133 см²
Слайд 22Дано:ABCD-трапеция
AB=CD, B=135°KD=3,4 см; AK=1,4 см
BK-высота
Найти: S трапеции ABCD
Решение:
1)в ΔABK K=90º ABK=135º- KBC=45º
A=90º- ABK=45º
2) Проведём высоту СE,
тогда KBCE-прямоугольник и BC=KE,а ΔDCE-прямоугольный, D=45º
3) ΔABK=ΔDCE по гипотенузе и острому углу(AB=CD, A= D)
DE=AK=1,4 см, значит KE=2см, BC=2см
4) AD=AK+KD=1,4+3,4=4,8см
SABCD= BK×(BC+AD)÷2
SABCD= 1,4×(2+4,8)÷2=4,76(см²)
Ответ:4,76см²
B
C
D
1,4 см
3,4 см
A
135°
К
E
