- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 6 ДЕРЕВЬЯ (продолжение) Нерекурсивные процедуры обхода бинарных деревьев Представления и реализации бинарных деревьев Примеры функций на бинарных деревьях БД с размеченными листьями Деревья Хаффмана (начало) презентация
Содержание
- 1. Лекция 6 ДЕРЕВЬЯ (продолжение) Нерекурсивные процедуры обхода бинарных деревьев Представления и реализации бинарных деревьев Примеры функций на бинарных деревьях БД с размеченными листьями Деревья Хаффмана (начало)
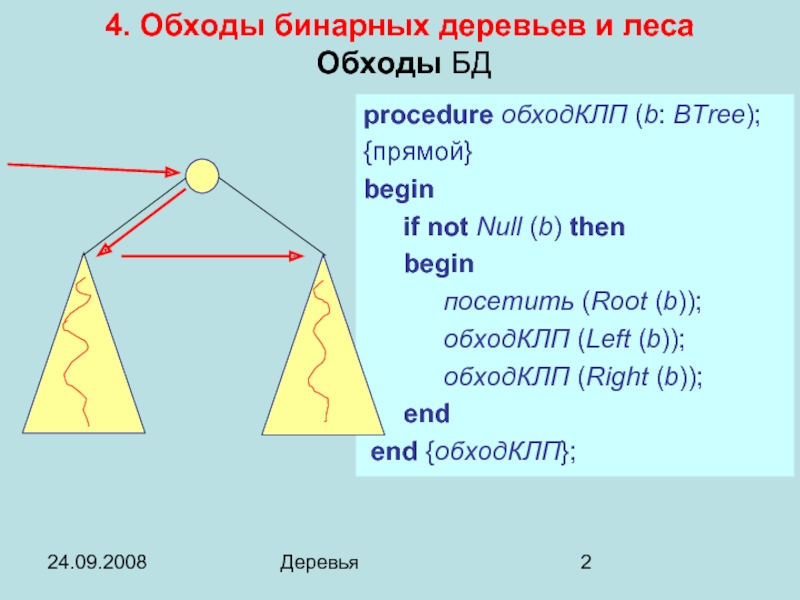
- 2. 24.09.2008 Деревья procedure обходКЛП (b: BTree);
- 3. 24.09.2008 Деревья Нерекурсивные процедуры обхода бинарных деревьев
- 4. 24.09.2008 Деревья В алгоритме: посетить корень – посетить
- 5. 24.09.2008 Деревья Общий алгоритм
- 6. 24.09.2008 Деревья Выполнение procedure обход (b: BTree)
- 7. 24.09.2008 Деревья КЛП Операция 1 –посетить (p); Операция
- 8. 24.09.2008 Деревья
- 9. 24.09.2008 Деревья лкп Операция 1 − if
- 10. 24.09.2008 Деревья
- 11. 24.09.2008 Деревья ЛПК См. пособие – фактически без упрощений
- 12. 24.09.2008 Деревья Обход БД в горизонтальном порядке (в ширину)
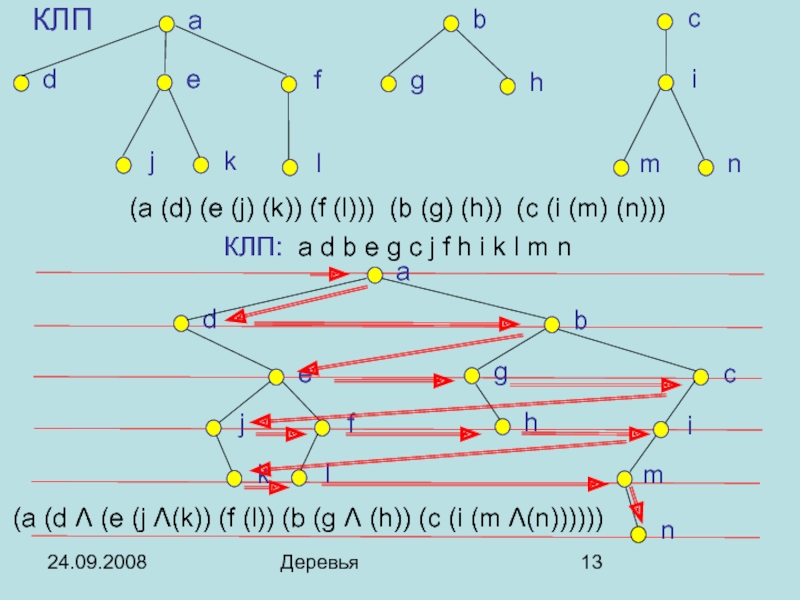
- 13. 24.09.2008 Деревья КЛП (a (d)
- 14. 24.09.2008 Деревья Представления и реализации бинарных См. учебное пособие «ДСД», п. 3.5
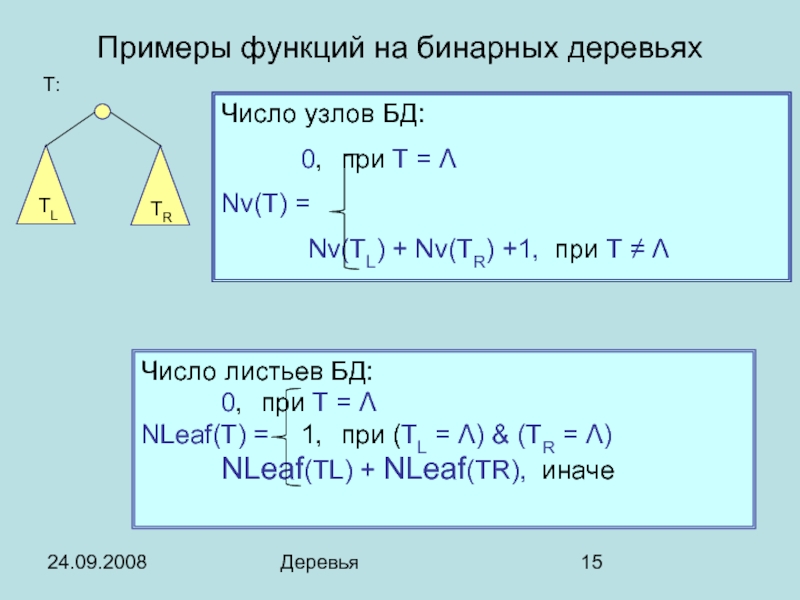
- 15. 24.09.2008 Деревья Примеры функций на бинарных деревьях
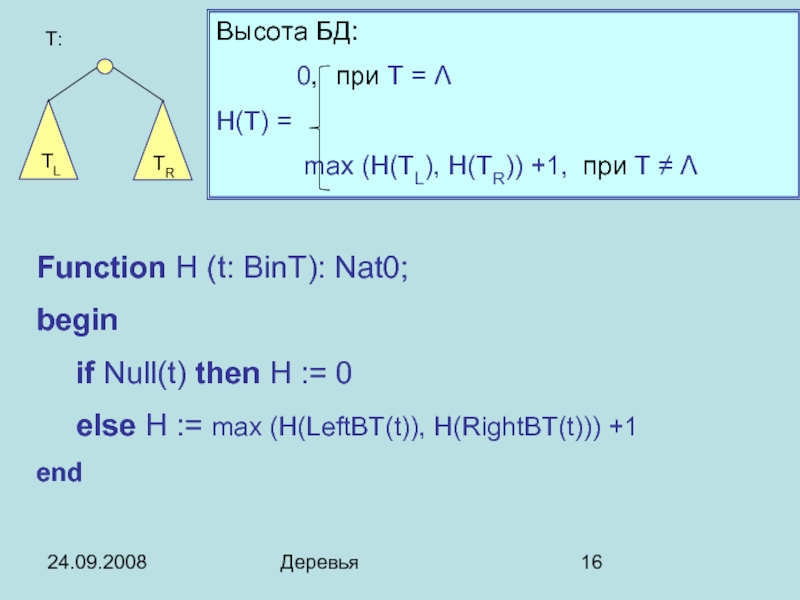
- 16. 24.09.2008 Деревья Высота БД: 0, при T
- 17. 24.09.2008 Деревья Проверить свойство дерева: для каждого
- 18. 24.09.2008 Деревья Бинарные деревья с размеченными листьями
- 19. 24.09.2008 Деревья БД → БД РЛ А
- 20. 24.09.2008 Деревья Деревья Хаффмана См. разделы пособия «ДКиП» 1.1.-1.4 (файлы MS Word)
- 21. 24.09.2008 Деревья КОНЕЦ ЛЕКЦИИ КОНЕЦ
Слайд 124.09.2008
Деревья
Структуры и алгоритмы обработки данных, 1
Лекция 6
ДЕРЕВЬЯ
(продолжение)
Нерекурсивные процедуры обхода
Представления и реализации бинарных деревьев
Примеры функций на бинарных деревьях
БД с размеченными листьями
Деревья Хаффмана (начало)
Слайд 224.09.2008
Деревья
procedure обходКЛП (b: BTree);
{прямой}
begin
if not Null (b) then
begin
посетить
обходКЛП (Left (b));
обходКЛП (Right (b));
end
end {обходКЛП};
4. Обходы бинарных деревьев и леса
Обходы БД
Слайд 324.09.2008
Деревья
Нерекурсивные процедуры обхода бинарных деревьев
В стеке S хранятся упорядоченные пары (p, n),
где p − узел бинарного дерева, а n − номер операции, которую надо применить к p, когда пара (p, n) будет выбрана из стека.
Операции
«посетить корень»,
«пройти левое поддерево»,
«пройти правое поддерево»
нумеруются числами 1, 2, 3 в зависимости от порядка их выполнения в данном варианте обхода.
Слайд 424.09.2008
Деревья
В алгоритме:
посетить корень – посетить (p);
пройти левое поддерево − if not Null (Left
then S ← (Left (p), 1);
пройти правое поддерево − if not Null (Right (p))
then S ← (Right (p), 1).
Для краткости использованы следующие обозначения операций со стеком:
S ← e вместо S := Push (e, S)
e ← S вместо Pop2 (e, S).
Слайд 624.09.2008
Деревья
Выполнение procedure обход (b: BTree)
Операции со стеком:
⇓(b, 1);
⇑(b, 1); ⇓(b,
⇑(b, 2); ⇓(b, 3); {начало Опер2}… ↓↑…{конец Опер2}
⇑(b, 3); {начало Опер3}… ↓↑…{конец Опер3}
Слайд 724.09.2008
Деревья
КЛП
Операция 1 –посетить (p);
Операция 2 − if not Null (Left (p)) then S
Операция 3 − if not Null (Right (p)) then S ← (Right (p), 1).
⇓(b, 1);
⇑(b, 1); ⇓(b, 2); посетить (p);
⇑(b, 2); ⇓(b, 3); if not Null (Left (p)) then ⇓(Left (p), 1); ⇑(Left (p), 1); …;
⇑(b, 3); if not Null (Right (p)) then ⇓(Right (p), 1);
⇑(Right (p), 1);…;
Слайд 924.09.2008
Деревья
лкп
Операция 1 − if not Null (Left (p)) then S ← (Left (p), 1);
Операция
Операция 3 − if not Null (Right (p)) then S ← (Right (p), 1).
Самостоятельно разобрать работу со стеком и обосновать корректность следующей процедуры.
Слайд 1324.09.2008
Деревья
КЛП
(a (d) (e (j) (k)) (f (l))) (b (g) (h)) (c
КЛП: a d b e g c j f h i k l m n
(a (d Λ (e (j Λ(k)) (f (l)) (b (g Λ (h)) (c (i (m Λ(n))))))
Слайд 1524.09.2008
Деревья
Примеры функций на бинарных деревьях
Число узлов БД:
0, при T = Λ
Nv(T)
Nv(TL) + Nv(TR) +1, при T ≠ Λ
Число листьев БД:
0, при T = Λ
NLeaf(T) = 1, при (TL = Λ) & (TR = Λ)
NLeaf(TL) + NLeaf(TR), иначе
Слайд 1624.09.2008
Деревья
Высота БД:
0, при T = Λ
H(T) =
max (H(TL), H(TR))
Function H (t: BinT): Nat0;
begin
if Null(t) then H := 0
else H := max (H(LeftBT(t)), H(RightBT(t))) +1
end
Слайд 1724.09.2008
Деревья
Проверить свойство дерева:
для каждого узла БД H(TL) – H(TR) = 1
Function
begin
if Null(t) then HB := True
else
begin
HL := H(LeftBT(t));
HR := H(RightBT(t));
HF := HF(LeftBT(t)) & HF(RightBT(t)) &
( (HL – HR) = 1)
end
end
! Пояснить неэффективность такой реализации функции HF
! Самостоятельно написать хороший вариант
Слайд 1824.09.2008
Деревья
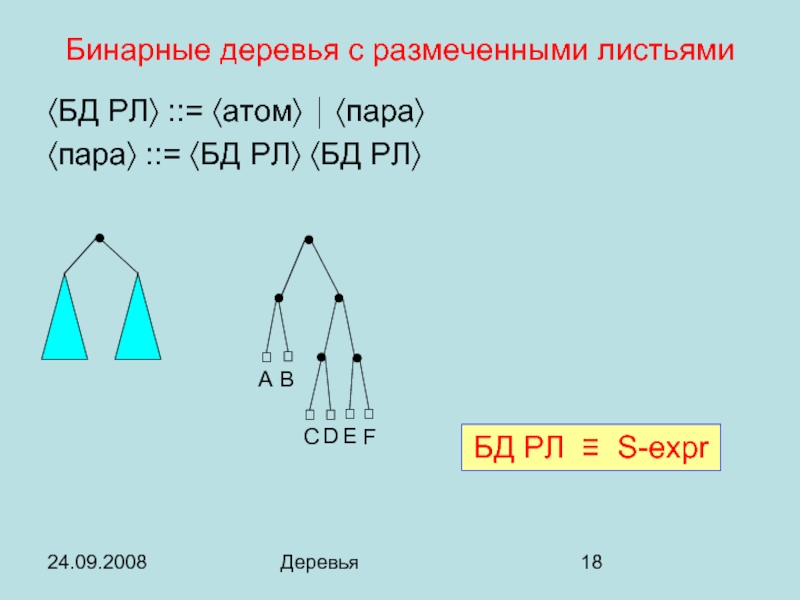
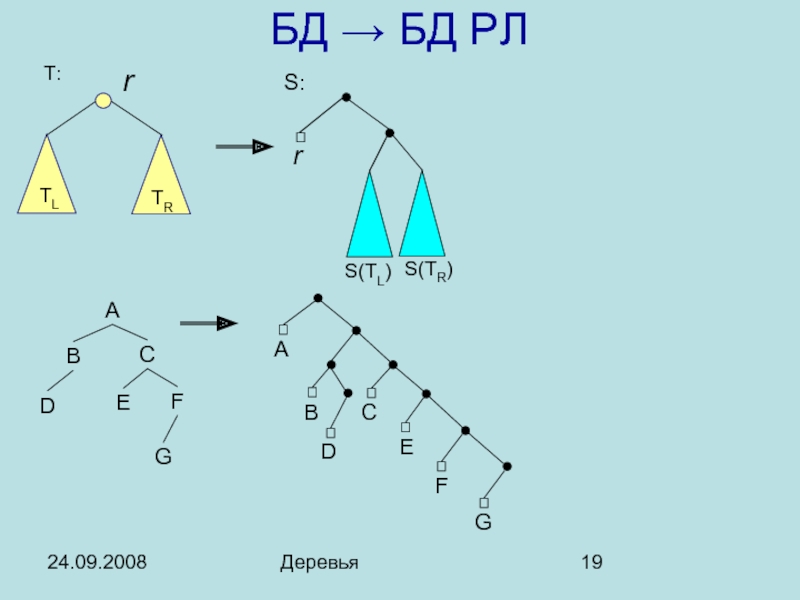
Бинарные деревья с размеченными листьями
〈БД РЛ〉 ::= 〈атом〉 ⏐ 〈пара〉
〈пара〉 ::=
F
E
D
C
B
А
БД РЛ ≡ S-expr
Слайд 2124.09.2008
Деревья
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ