- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции и графики. презентация
Содержание
- 1. Функции и графики.
- 2. Линейная функция Обратная пропорциональность Задачи ГИА
- 3. Линейная зависимость y=kx+b K>0, b>0 K>0, b=0 K>0, b
- 4. На рисунке изображены графики функций вида y=kx+b.
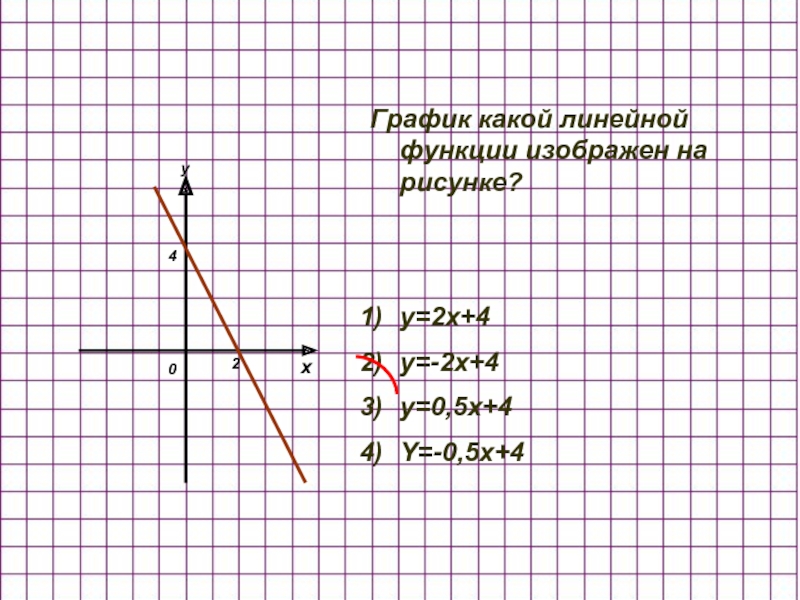
- 5. x y 2 4 График какой линейной
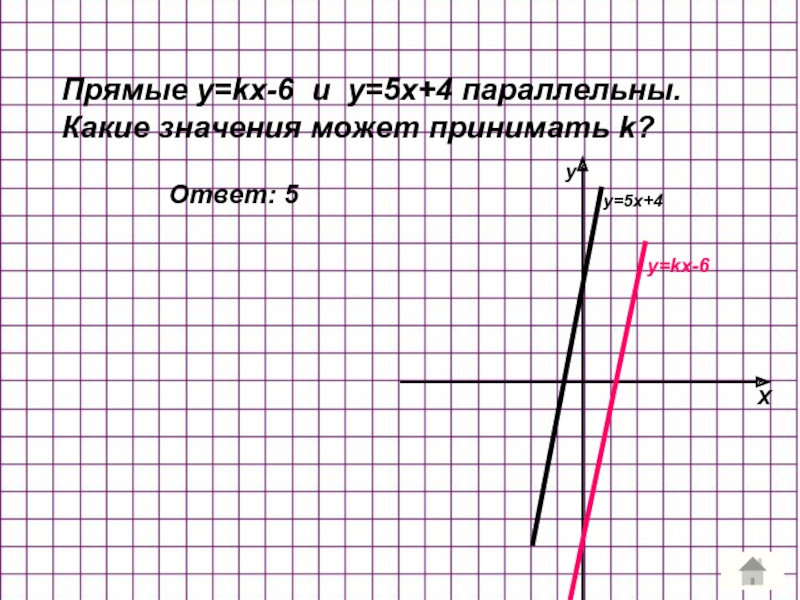
- 6. Прямые y=kx-6 и у=5x+4 параллельны. Какие значения
- 7. Запишите уравнение квадратичной функции:
- 8. Запишите уравнение квадратичной функции:
- 9. 0 1 1 2 х y На
- 10. Нули функции. x y A На рисунке
- 11. На каком рисунке изображен график этой функции,
- 13. Y=1-x2 x+4=0 x+y=4 y+10=0 На рисунке изображены
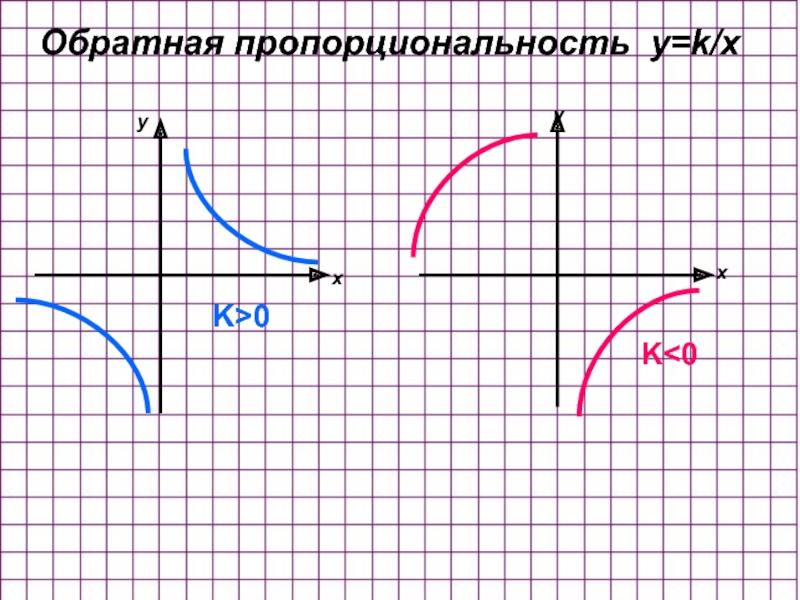
- 14. Обратная пропорциональность y=k/x K>0 K
- 15. 3 4 1
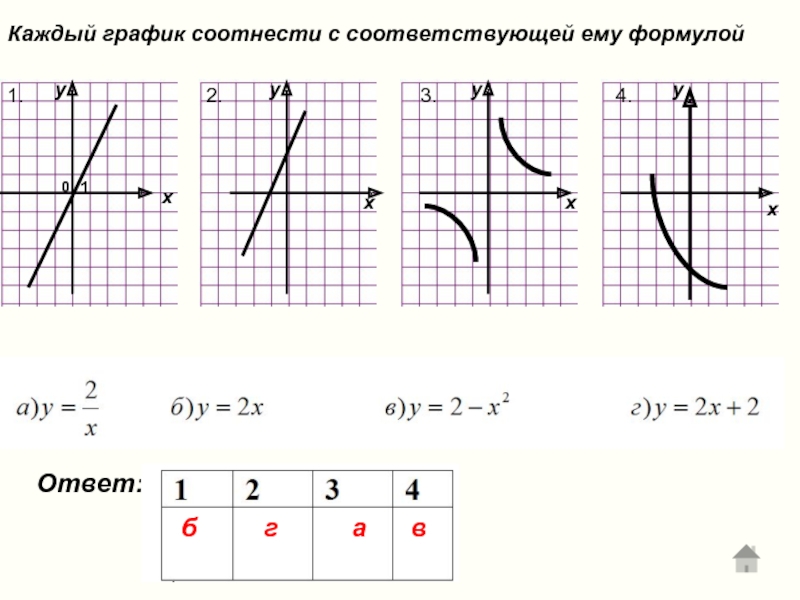
- 16. Каждый график соотнести с соответствующей ему формулой
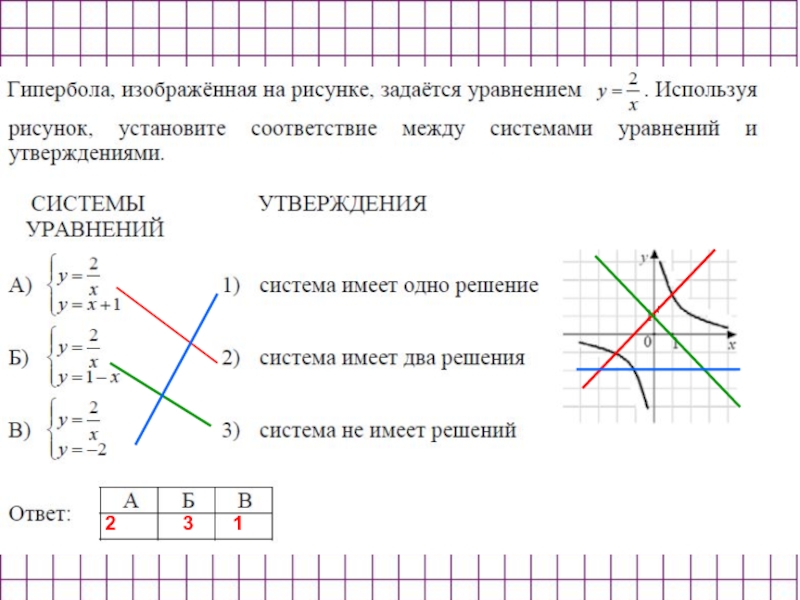
- 18. 2 3 1
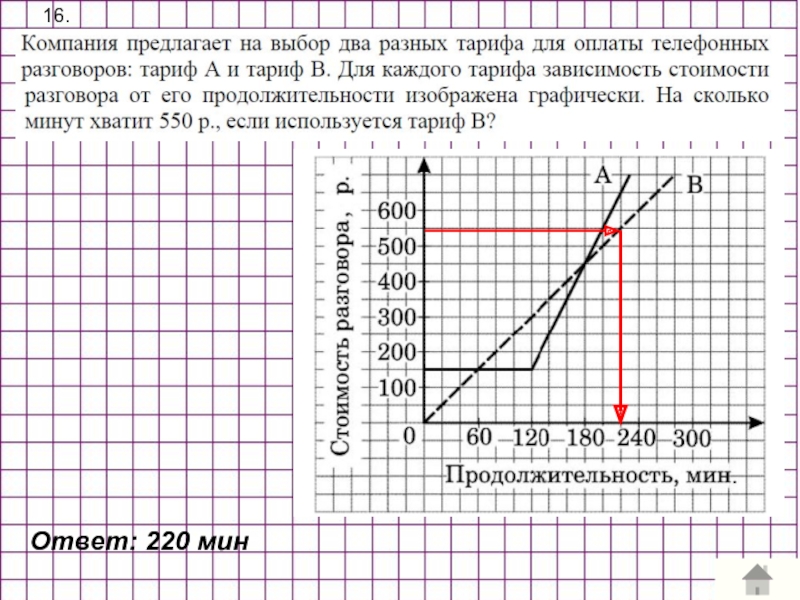
- 19. 16. Ответ: 220 мин
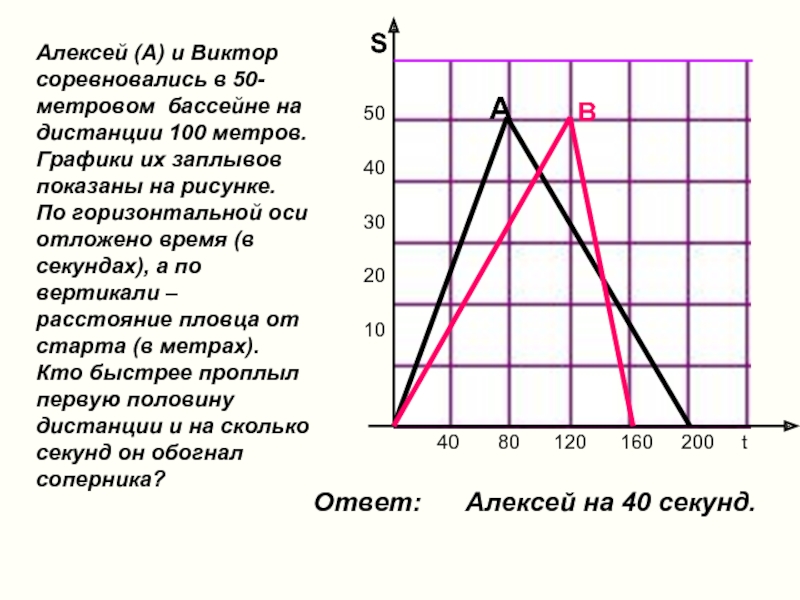
- 20. Алексей (А) и Виктор соревновались в 50-метровом
- 22. Постройте график функции
- 23. Свойства функции. 1. Область определения функции
- 24. 2. Область значений, ограниченность. Область значений –
- 25. Функция задана
- 26. 3. Нули функции, промежутки знакопостоянства.
- 27. 4. Монотонность функции. Функция
- 28. Задача. По графику функции, область определения которой
- 29. 5. Четность и нечетность функций. Функция
- 30. Задача. Дан фрагмент графика нечетной функции
- 31. Задача. Определите какие из функций, графики
- 32. При каких значениях p прямая y=p имеет
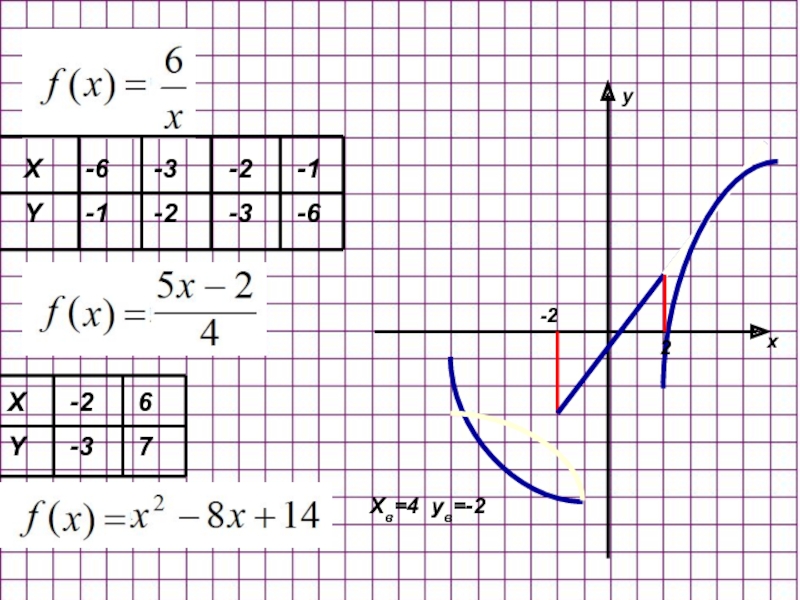
- 33. X -6 -3
- 34. При каких значениях p прямая y=p имеет
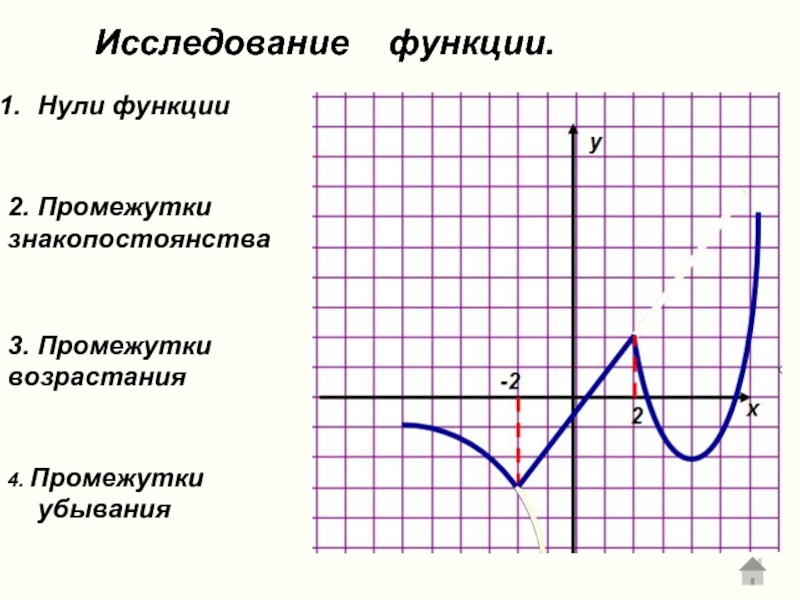
- 35. Исследование функции. Нули функции
- 36. Тест по теме функции и графики №1
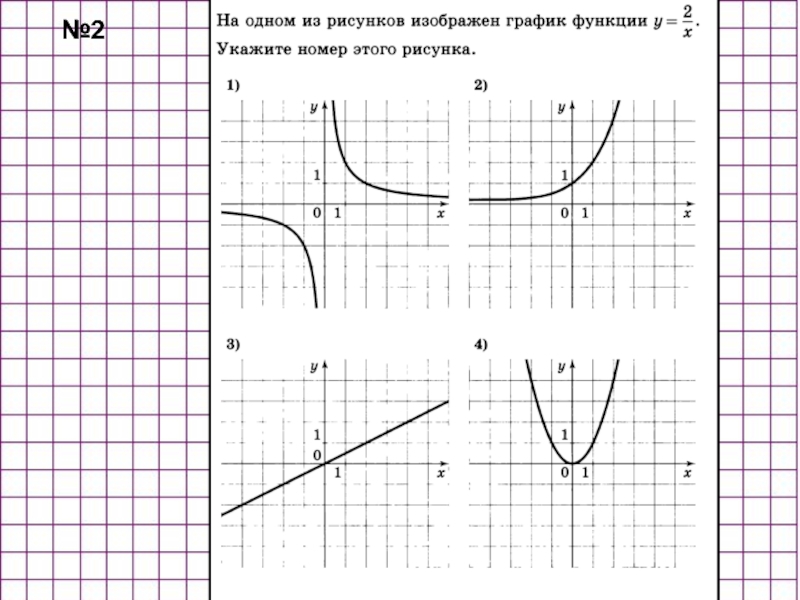
- 37. №2
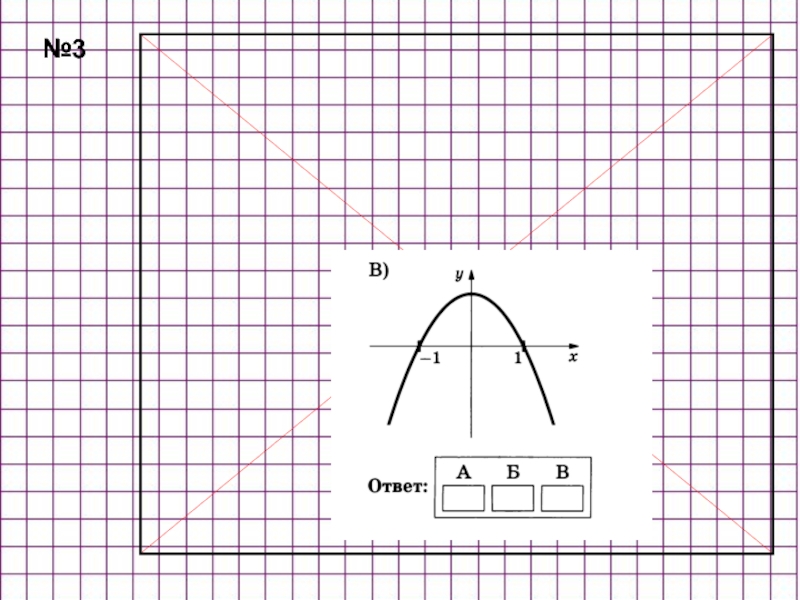
- 38. №3
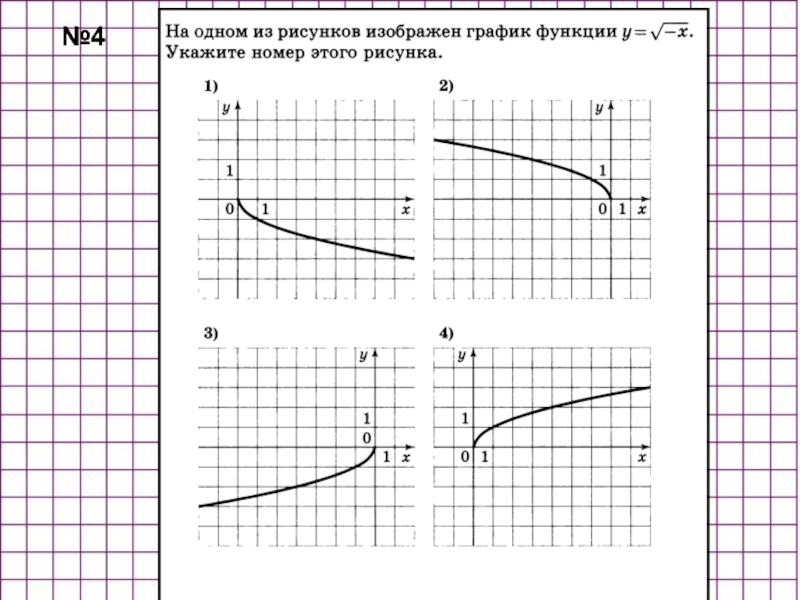
- 39. №4
- 40. №5
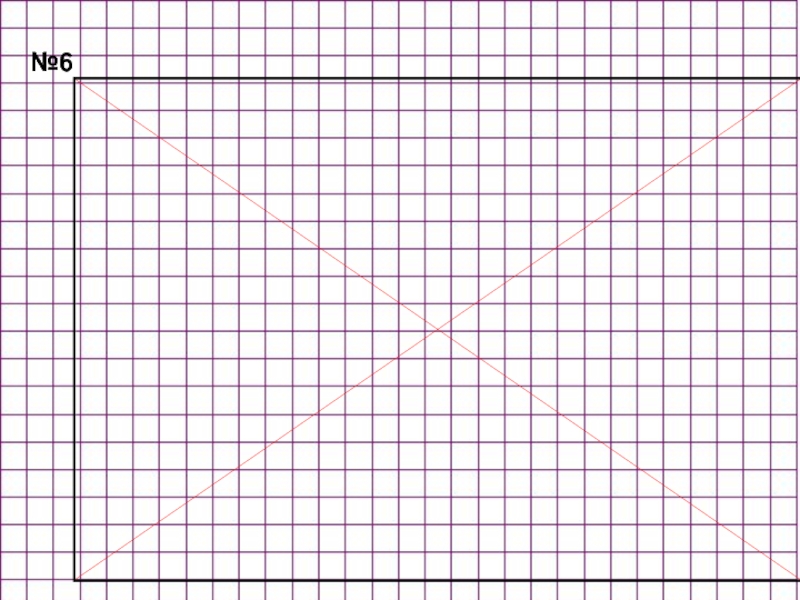
- 41. №6
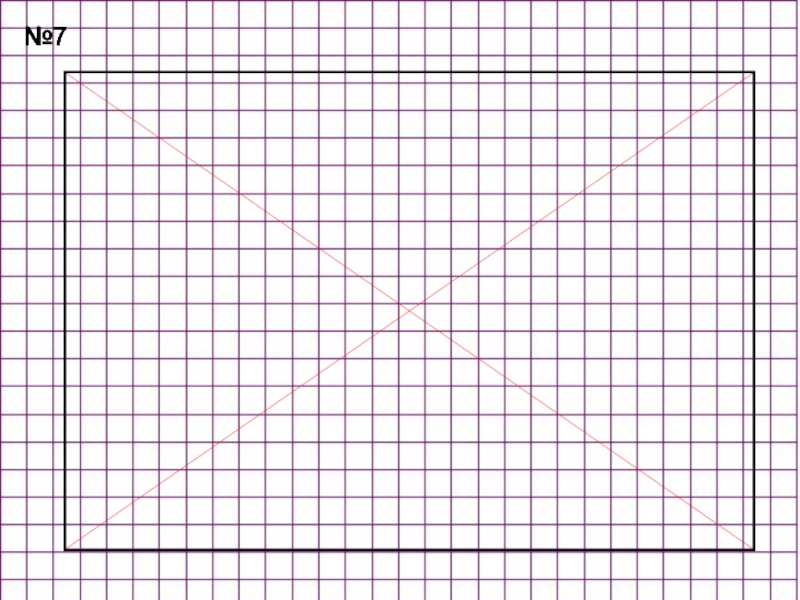
- 42. №7
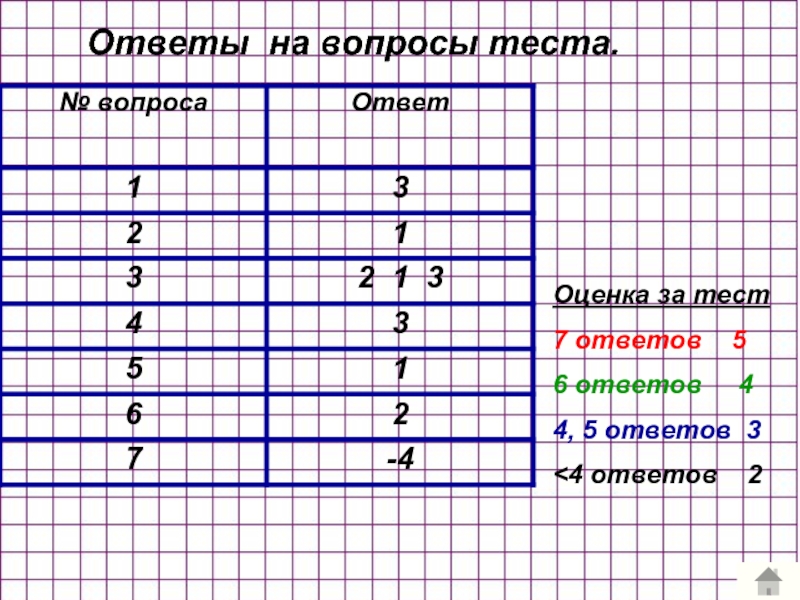
- 43. Ответы на вопросы теста. Оценка за тест
Слайд 2Линейная функция
Обратная пропорциональность
Задачи ГИА
Квадратичная функция
Свойства функций
Построение графика кусочной функции и её
Тестовая работа
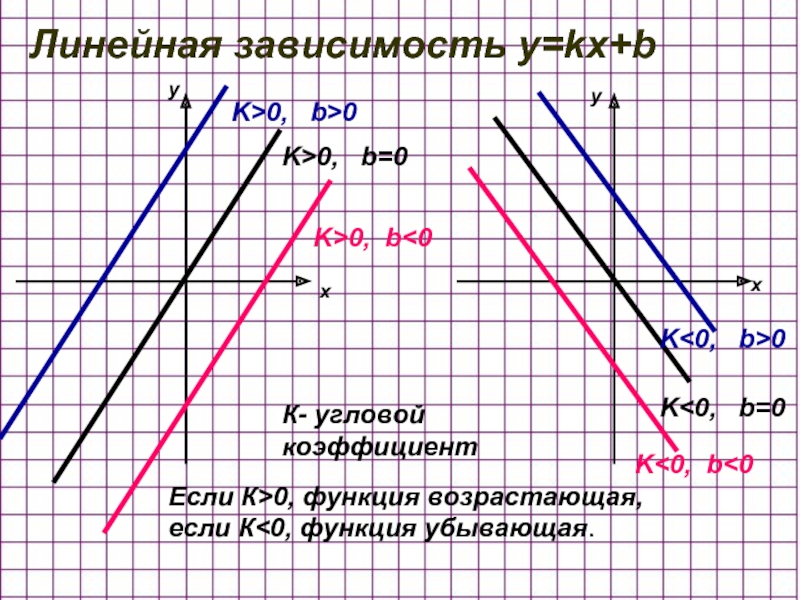
Слайд 3Линейная зависимость y=kx+b
K>0, b>0
K>0, b=0
K>0, b
x
x
К- угловой коэффициент
y
y
Если К>0, функция возрастающая, если К<0, функция убывающая.
Слайд 4На рисунке изображены графики функций вида y=kx+b.
Установите соответствие между графиками и
а)k>0, b>0 б) k<0, b>0 в) k<0, b<0
Ответ:
1.
2.
3.
x
x
x
y
y
y
в а б
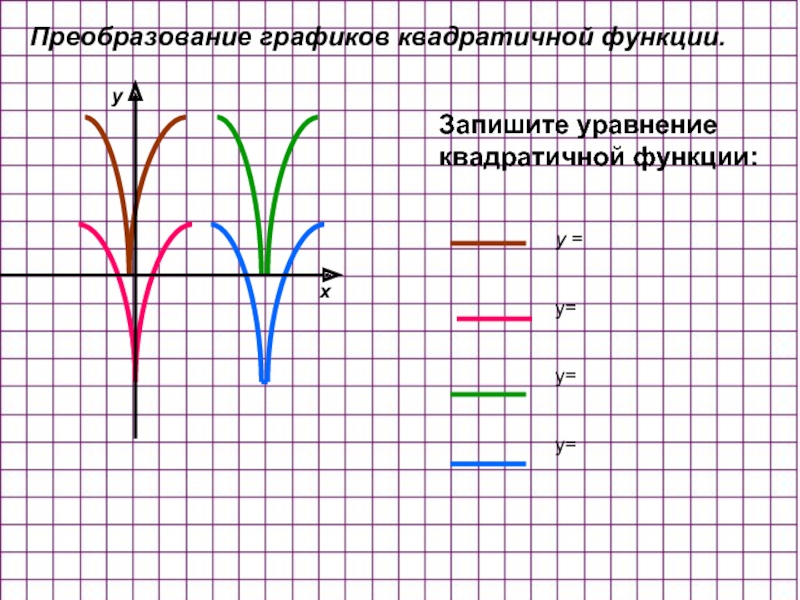
Слайд 7Запишите уравнение квадратичной функции:
y=
y=
y=
Преобразование графиков квадратичной функции.
x
y
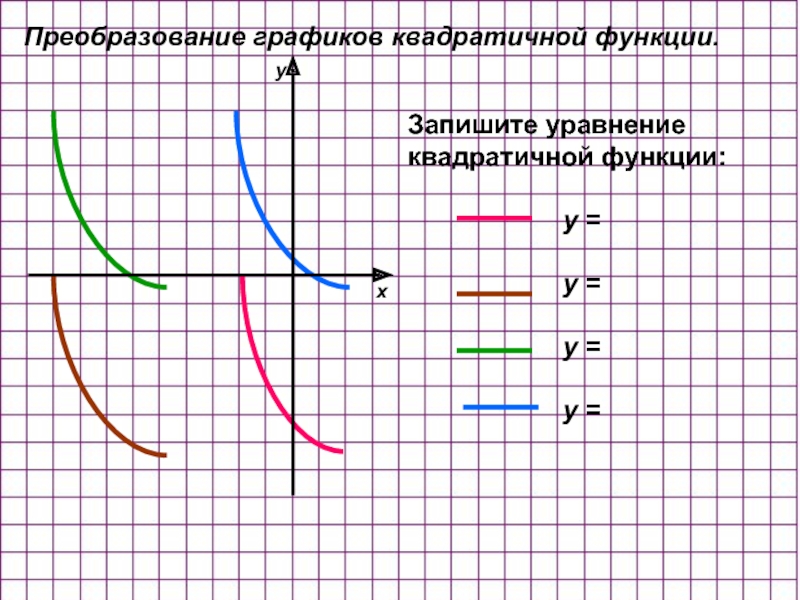
Слайд 8Запишите уравнение квадратичной функции:
y =
y =
y =
Преобразование графиков квадратичной функции.
x
y
Слайд 90
1
1
2
х
y
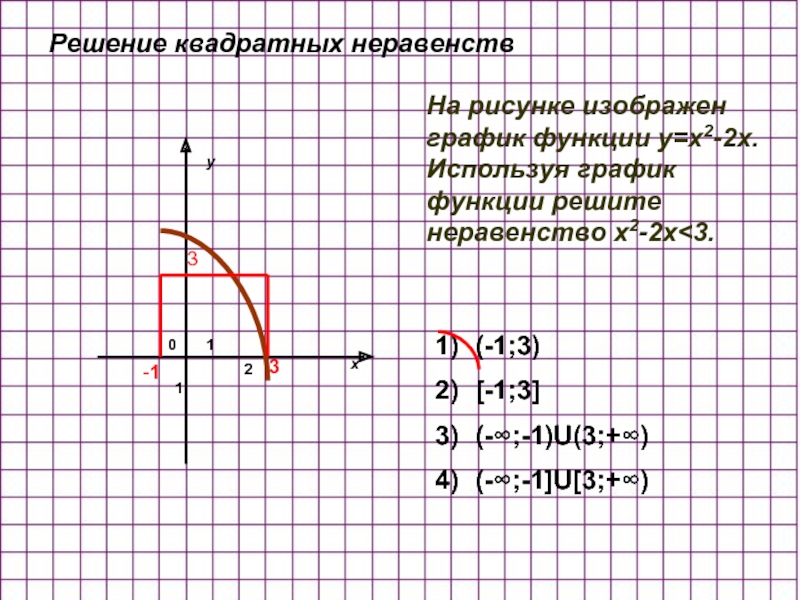
На рисунке изображен график функции y=x2-2x. Используя график функции решите неравенство
(-1;3)
[-1;3]
(-∞;-1)U(3;+∞)
(-∞;-1]U[3;+∞)
Решение квадратных неравенств
3
-1
3
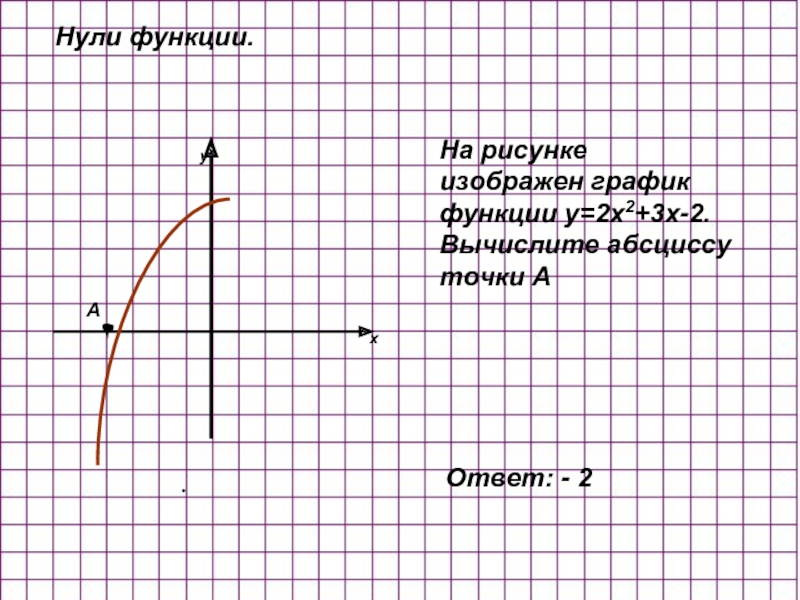
Слайд 10Нули функции.
x
y
A
На рисунке изображен график функции y=2x2+3x-2. Вычислите абсциссу точки А
Ответ:
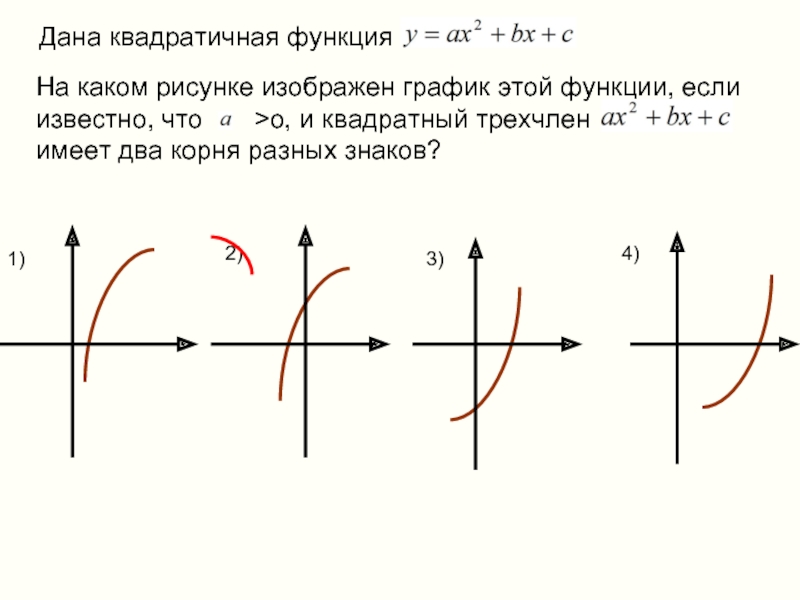
Слайд 11На каком рисунке изображен график этой функции, если известно, что
Дана квадратичная функция
1)
2)
3)
4)
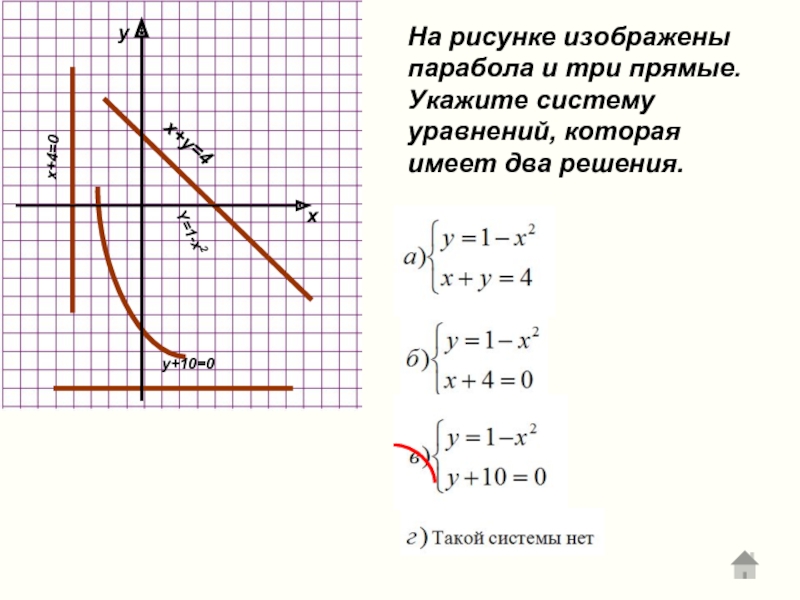
Слайд 13Y=1-x2
x+4=0
x+y=4
y+10=0
На рисунке изображены парабола и три прямые. Укажите систему уравнений, которая
x
y
Слайд 20Алексей (А) и Виктор соревновались в 50-метровом бассейне на дистанции 100
S
40 80 120 160 200 t
50
40
30
20
10
А
В
Ответ: Алексей на 40 секунд.
Слайд 210 1
t(ч)
S(км)
100
80
60
40
20
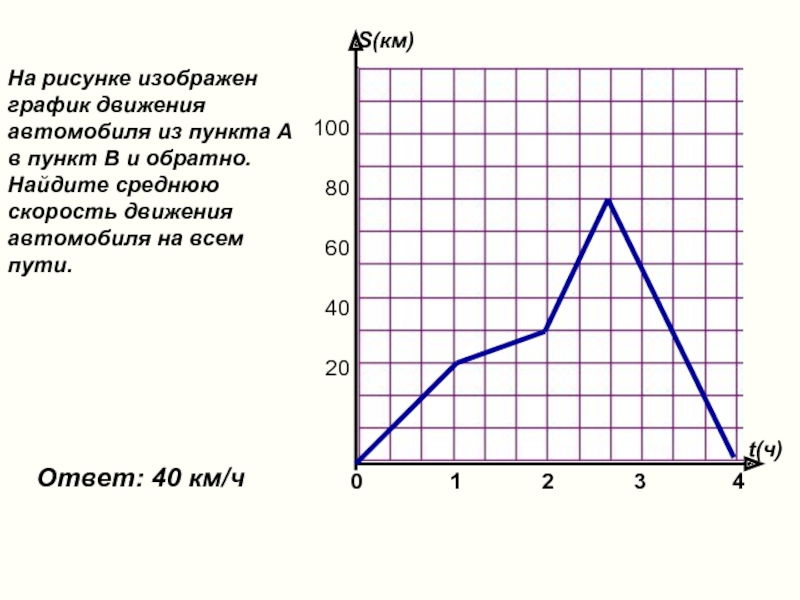
На рисунке изображен график движения автомобиля из пункта А в пункт В и обратно. Найдите среднюю скорость движения автомобиля на всем пути.
Ответ: 40 км/ч
Слайд 22
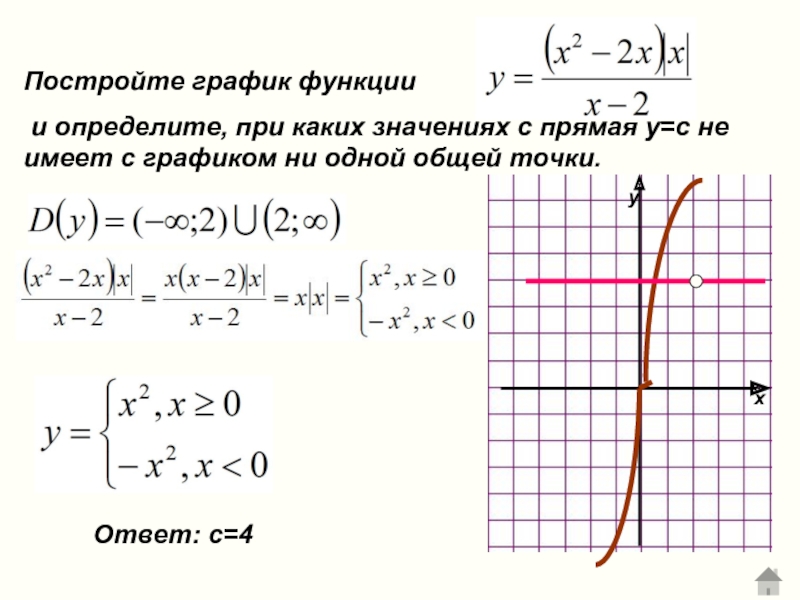
Постройте график функции
x
y
Ответ: с=4
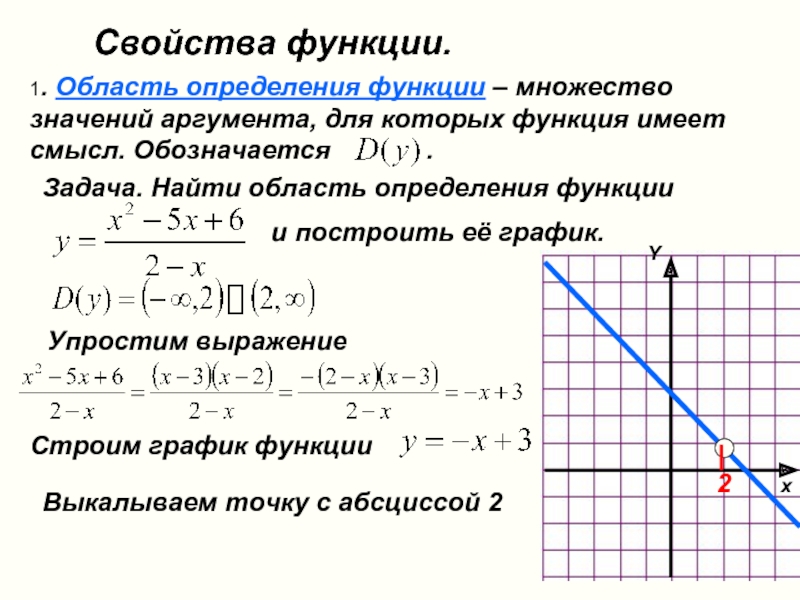
Слайд 23Свойства функции.
1. Область определения функции – множество значений аргумента, для
Задача. Найти область определения функции
и построить её график.
Упростим выражение
x
Строим график функции
Y
Выкалываем точку с абсциссой 2
2
Слайд 242. Область значений, ограниченность.
Область значений – множество значений функции, обозначается
Функция ограничена
выполняется неравенство
где –некоторое число.
,
Функция ограничена сверху, если для любого
выполняется неравенство
,
где –некоторое число.
Функция называется ограниченной, если для любого
выполняется неравенство
где –некоторые числа.
Слайд 25Функция задана графиком, на области определения
x
y
Наименьшее значение
Наибольшее значение
Слайд 274. Монотонность функции.
Функция называется возрастающей на множестве
Функция называется убывающей на множестве Х, если большему значению аргумента соответствует меньшее значение функции.
Функцию, возрастающую на множестве Х или убывающую на множестве Х, называют монотонной функцией на множестве Х.
Слайд 28Задача. По графику функции, область определения которой [-6,7], укажите промежутки монотонности
Х
-3
1
3
6
7
Функция возрастает
Функция убывает
Слайд 295. Четность и нечетность функций.
Функция называется четной, если для
верно равенство
Функция называется нечетной, если для
любого верно равенство
Область определения четной и нечетной функции есть множество симметричное относительно нуля
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат
Слайд 30
Задача. Дан фрагмент графика нечетной функции
x
y
на
на
возрастает на
Убывает на
Слайд 31
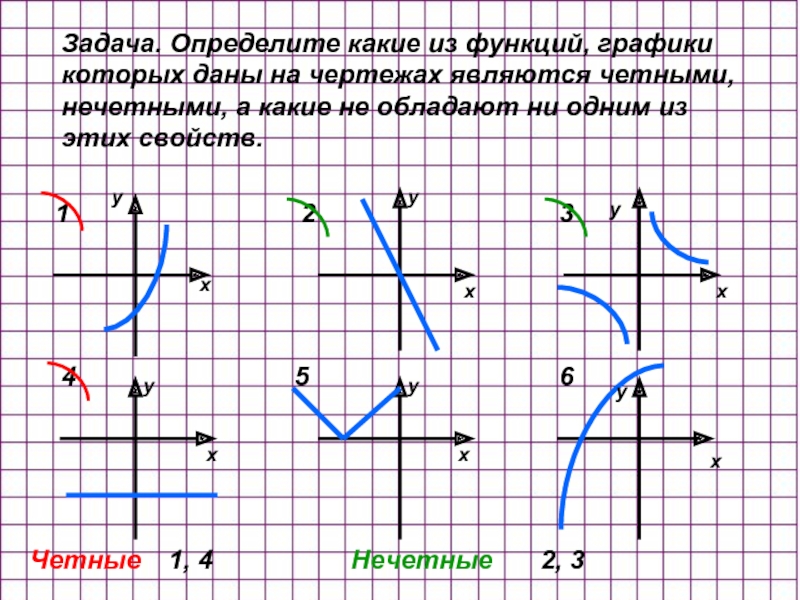
Задача. Определите какие из функций, графики которых даны на чертежах являются
x
y
x
x
x
x
x
y
y
y
y
y
1
2
3
4
5
6
Четные
1, 4
Нечетные
2, 3
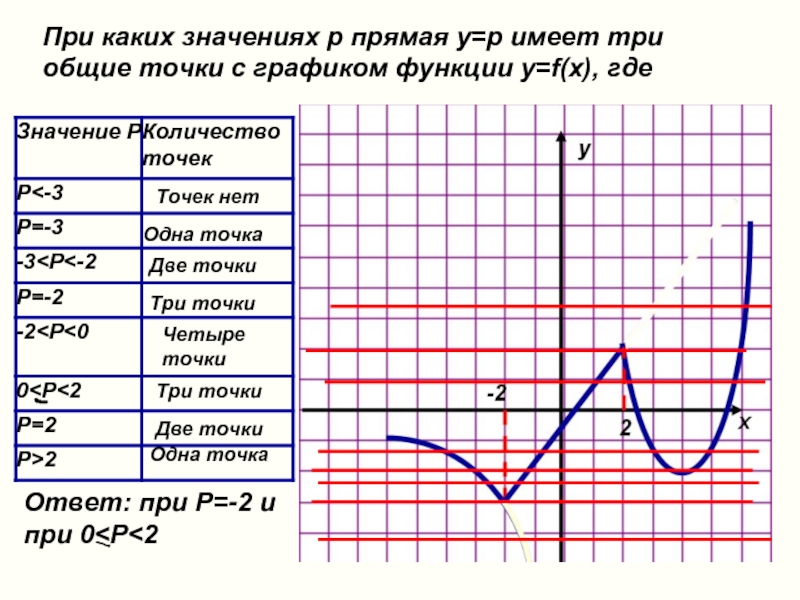
Слайд 32При каких значениях p прямая y=p имеет три общие точки с
Построение графика кусочной функции и её исследование.
Слайд 34При каких значениях p прямая y=p имеет три общие точки с
Точек нет
Одна точка
Две точки
Три точки
Четыре точки
Три точки
Две точки
Одна точка
Ответ: при Р=-2 и при 0






![Функция задана графиком, на области определения [-3;7], найдите её наименьшее и наибольшее значения,](/img/tmb/1/1273/c636697a1ca7df199ead3c31a1595b6b-800x.jpg)

![Задача. По графику функции, область определения которой [-6,7], укажите промежутки монотонности функции. Х-31367Функция возрастаетФункция убывает](/img/tmb/1/1273/10392f58c4f3d275e569f8dc154b793b-800x.jpg)

![Задача. Дан фрагмент графика нечетной функции которая определена на [-7;7] достройте график](/img/tmb/1/1273/510aff140ef8f8c52912df2394ba22a9-800x.jpg)