- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрия 8 класс презентация
Содержание
- 1. Геометрия 8 класс
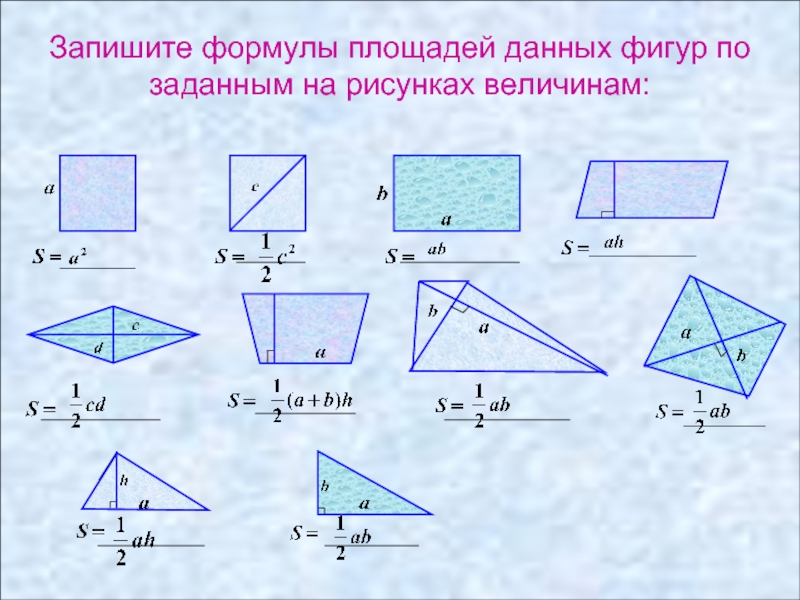
- 2. Запишите формулы площадей данных фигур по заданным на рисунках величинам:
- 4. Т Е О Р Е М
- 5. Пифагор Самосский (ок. 580 – ок. 500 г. до н.э.)
- 6. Эмблемой или опознавательным знаком союза являлась
- 7. Этот пятиугольник обладает интересным геометрическим свойством:
- 8. Открытия пифагорейцев Пифагорейцами было сделано много
- 9. Видел в математике он свет, Как
- 10. Если бы нам удалось вступить в
- 11. Пребудет вечная истина, как скоро
- 12. Формулировка теоремы во времена Пифагора
- 18. Итак, Если дан нам треугольник И
- 19. Задача Р е ш е н
- 20. Р е ш е н и
- 21. Задача из учебника «Арифметика»
- 22. Задача индийского математика XII века
- 23. Задача из китайской «Математики в
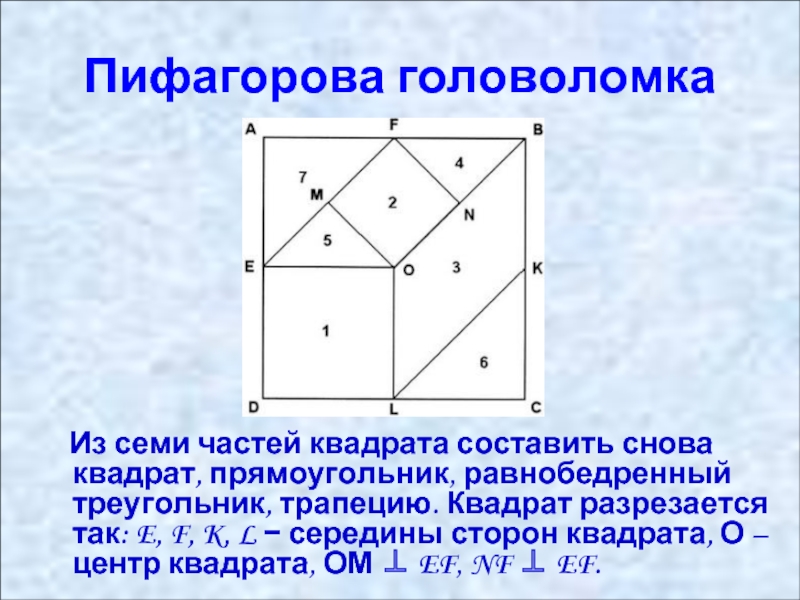
- 24. Пифагорова головоломка Из
- 25. Пифагор (?). Бронзовый бюст. Римская копия
- 26. Шаржи
- 28. Самосская монета с изображением Пифагора.
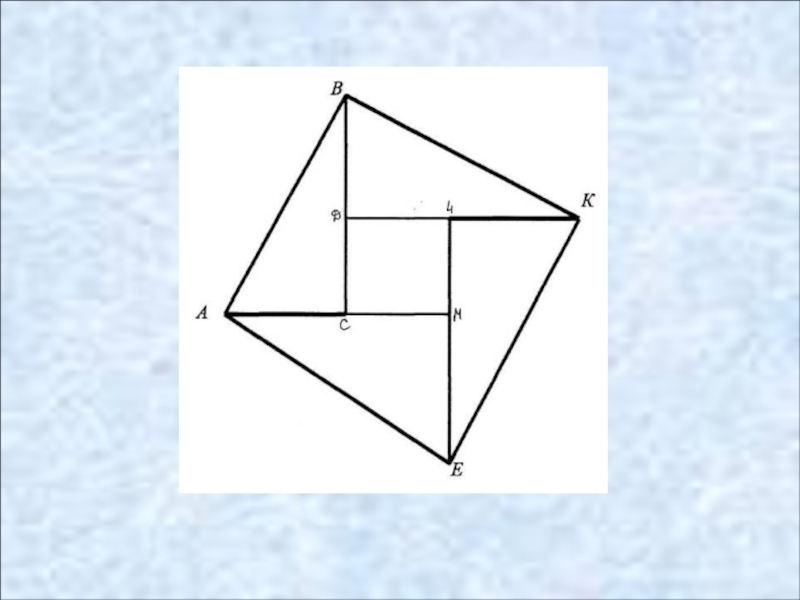
Слайд 3
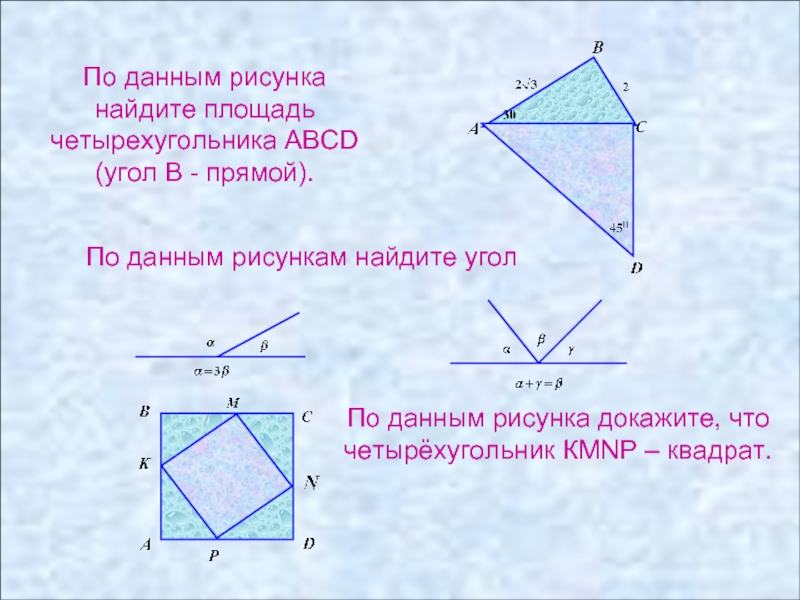
По данным рисунка докажите, что
четырёхугольник КМNР – квадрат.
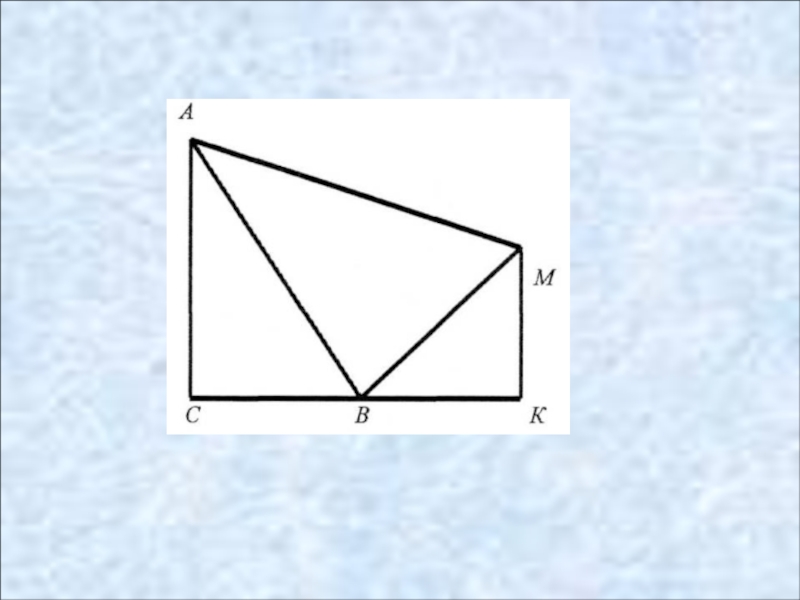
По данным рисунка найдите площадь четырехугольника ABCD (угол В - прямой).
По данным рисункам найдите угол
Слайд 4
Т Е О Р Е М А
П И Ф А
Часть картины "Школа Афин" изображающая Пифагора, автор Rafaello Sanzio
Слайд 6
Эмблемой или опознавательным знаком союза являлась пентаграмма– пятиконечная звезда. Пентаграмме присваивалась
У немецкого поэта Гёте в трагедии "Фауст", которую вы будете изучать на уроках литературы, описывается случай, когда дьявол Мефистофель проник в жилище учёного Фауста, потому что пентаграмма на его доме была плохо начерчена, и промежуток в уголке остался. Зачитаю вам эпизод.
Мефистофель: Нет, трудновато выйти мне теперь,
Тут кое-что мешает мне немного:
Волшебный знак у вашего порога.
Фауст: Не пентаграмма ль этому виной?
Но как же, бес, пробрался ты за мной?
Каким путем впросак попался?
Мефистофель: Изволили ее вы плохо начертить,
И промежуток в уголку остался,
Там, у дверей, и я свободно мог вскочить.
Слайд 7
Этот пятиугольник обладает интересным геометрическим свойством: поворотной симметрией пятого порядка, т.е.
Слайд 8
Открытия пифагорейцев
Пифагорейцами было сделано много важных
открытий в арифметике и геометрии,
теорема о сумме внутренних углов треугольника;
построение правильных многоугольников и деление плоскости на некоторые из них;
геометрические способы решения квадратных уравнений;
деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;
доказательство того, что корень из 2 не является рациональным числом;
создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.
Слайд 9
Видел в математике он свет,
Как художник, как большой поэт.
Слайд 10
Если бы нам удалось вступить в контакт с разумными веществами какой
Джованни Скиапарелли (1835 - 1910)
Слайд 11
Пребудет вечная истина, как скоро
Ее познает слабый человек!
И ныне
Слайд 12
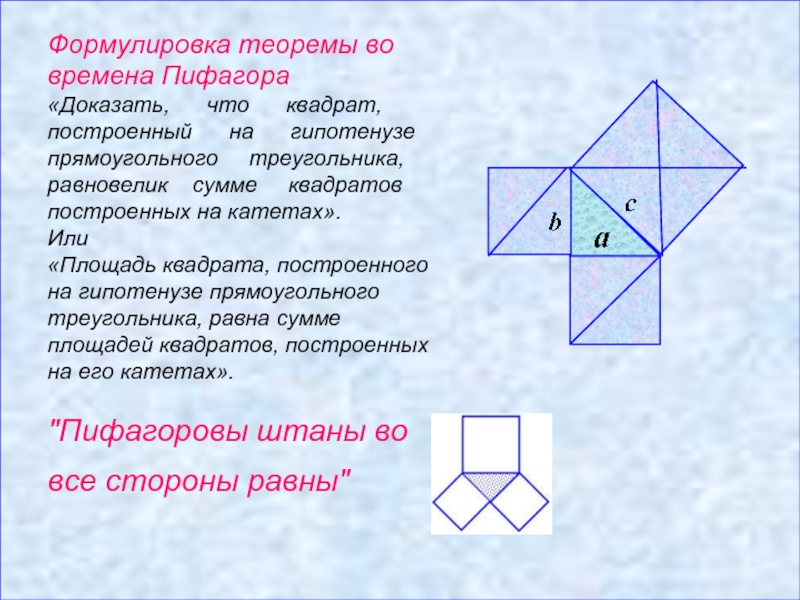
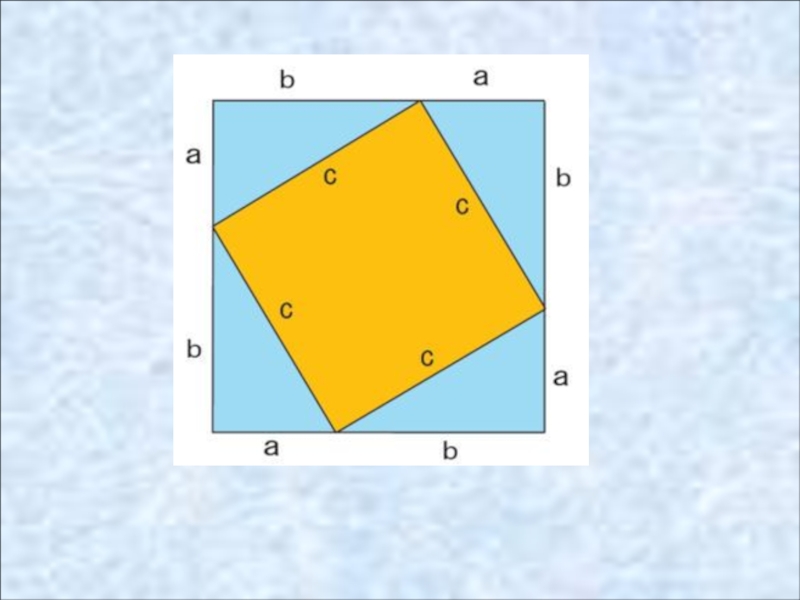
Формулировка теоремы во времена Пифагора
«Доказать, что
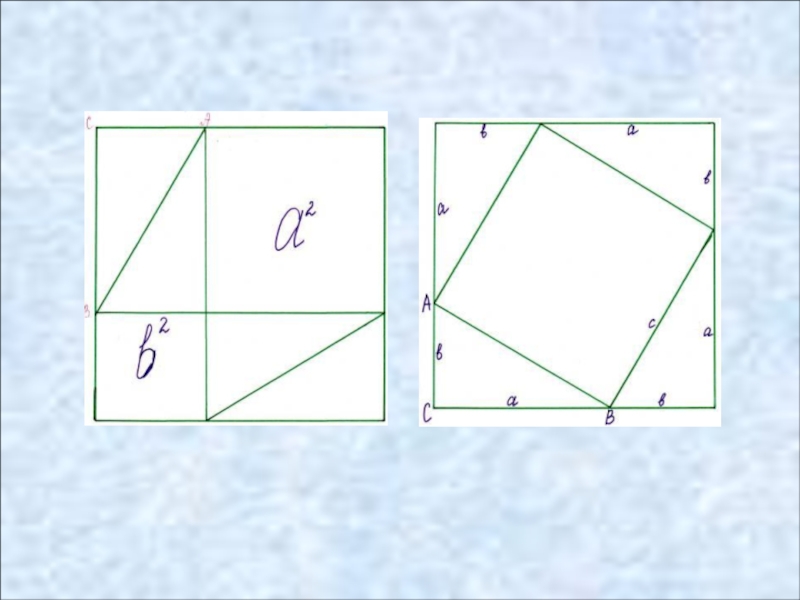
Слайд 13
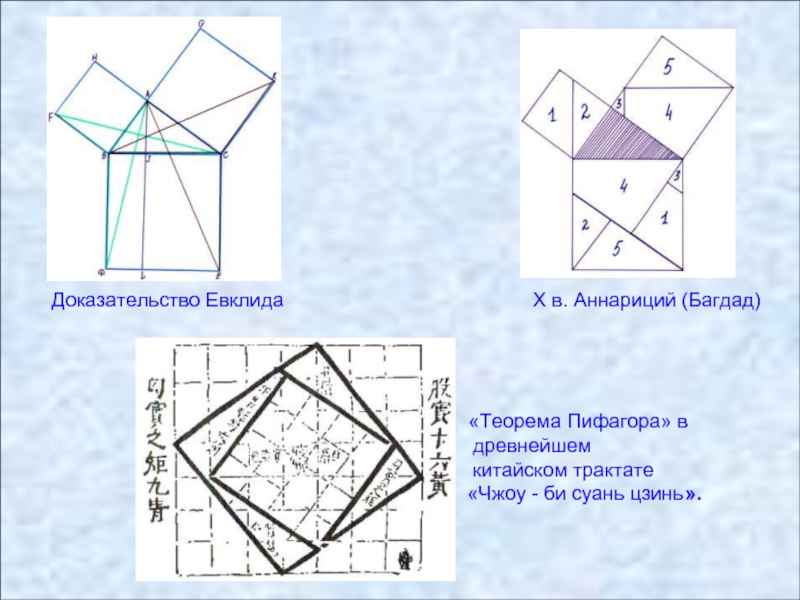
Доказательство Евклида X в. Аннариций (Багдад)
«Теорема Пифагора» в
древнейшем
китайском трактате
«Чжоу - би суань цзинь».
Слайд 18
Итак,
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
Слайд 19
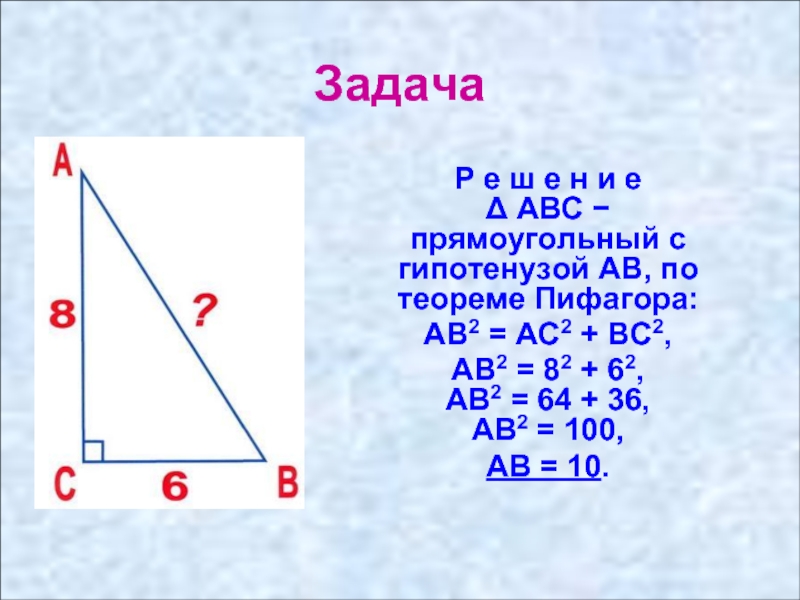
Задача
Р е ш е н и е
АВ2 = АС2 + ВС2,
АВ2 = 82 + 62, АВ2 = 64 + 36, АВ2 = 100,
АВ = 10.
Слайд 20
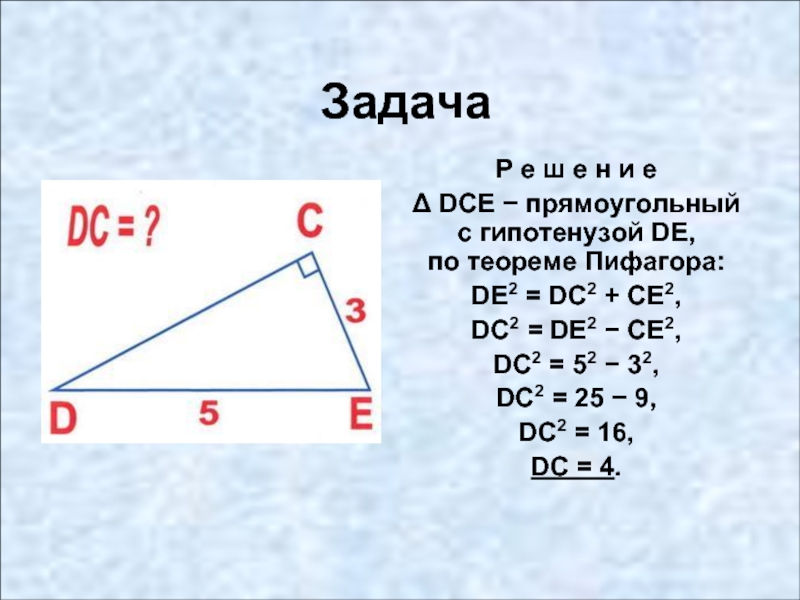
Р е ш е н и е
Δ DCE − прямоугольный с
DE2 = DС2 + CE2,
DC2 = DE2 − CE2,
DC2 = 52 − 32,
DC2 = 25 − 9,
DC2 = 16,
DC = 4.
Задача
Слайд 21
Задача из учебника «Арифметика»
Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.
Слайд 22
Задача индийского математика
XII века Бхаскары
На берегу реки рос тополь одинокий.
Вдруг
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»